ПРЕДМЕТ СТАТИСТИЧЕСКОЙ НАУКИ И ЕЕ МЕТОДОЛОГИЯ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

УТВЕРЖДАЮ

Проректор по учебной работе

_________________Е.В.Никифорова

«_____»___________________2005г.

Теория статистики)

Учебно-методическое пособие, методические указания

и задания к контрольной (индивидуальной) работе

для студентов экономических специальностей

Составил – к.э.н., доцент Гениатулин В.Н.

Тольятти 2005

Учебно-методическое пособие разработано в соответствии с Государственными образовательными стандартами специальностей 060400 «Финансы и кредит»,

060500 «Бухгалтерский учет, анализ и аудит»,

061100 «Менеджмент организации», 061500 «Маркетинг»,

351200 «Налоги и налогообложение»

Рассмотрены на заседании кафедры «Бухгалтерский учет, анализ и аудит»

Протокол №____от_____________2005г.

Зав. кафедрой «Бухгалтерский учет, анализ и аудит»____Е.В.Никифорова

Одобрено УМС экономического факультета

Протокол №____от_____________2005г.

Утверждено на заседании УМС ВУиТ

Протокол №____от_____________2005г.

Председатель УМС ВУиТ__________________Е.В.Никифорова

Содержание

1. Предмет статистической науки и ее методология

2. Содержание курса

3. Методические указания по выполнению контрольной работы

4. Задания к контрольной работе

5. Практикум по теории статистики

6. Вопросы к экзамену (зачету) по статистике

7. Тесты

8. Учебно-методическое обеспечение дисциплины

СОДЕРЖАНИЕ КУРСА

Тема I . Предмет и метод, задачи и организация статистической науки.

Понятие о статистике как науке и статистическом исследовании.

Возникновение учета и статистики.

Предмет статистической науки. Место статистики в системе наук.

Метод статистики. Закон больших чисел и его роль в изучении статистических закономерностей. Границы статистического познания.

Разделы статистики. Общая теория статистики, её предмет и содержание. Связь общей теории статистики с социально-экономической и отраслевыми статистиками.

Основные категории и понятия статистики. Статистическая совокупность. Единица совокупности. Признак, измерение признаков, вариация признаков. Статистический показатель, система показателей.

Современная организация и задачи статистики в Российской Федерации. Задачи перехода на международную практику статистики. Международные органы статистики.

Тема II . Статистическое наблюдение.

Понятие о статистическом наблюдении. Основные организационные формы, виды и способы статистического наблюдения. Точность наблюдения.

Понятие и основные этапы статистического исследования. Статистическое наблюдение – первый этап статистического исследования. Объект наблюдения, единица наблюдения. Организационные формы и виды статистического наблюдения: по времени регистрации фактов (текущее, периодическое, единовременное), по охвату единиц изучаемого объекта (сплошное и несплошное), по способу сбора информации (отчетность и специально-организованное). План статистического наблюдения и его составные части.

Организационный план и программа статистического наблюдения. Статистические формуляры и принципы их разработки.

Ошибки наблюдения. Обеспечение точности статистического наблюдения.

Проблемы организации статистического наблюдения в современных условиях и его роль в информационном обеспечении органов исполнительной власти и других пользователей.

Тема III . Методы обработки и анализа статистической информации.

Понятие о статистической таблице, ее основные элементы. Виды таблиц по характеру подлежащего и сказуемого. Основные правила построения таблиц. Чтение и анализ таблиц.

Понятие о статистическом графике, его основные элементы. Классификация видов графиков. Диаграммы. Статистические карты.

ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ

ВАРИАНТ ПЕРВЫЙ

Задача 1

Имеются следующие отчетные данные 25 заводов одной из отраслей промышленности:

Номер завода	Среднегодовая стоимость основных производственных фондов, млн. руб.@	Валовая продукция в сопоставимых ценах, млн. руб.
1	6,9	10,0
2	8,9	12,0
3	3,0	3,5
4	5,7	4,5
5	3,7	3,4
6	5,6	8,8
7	4,5	3,5
8	7,1	9,6
9	2,5	2,6
10	10,0	13,9
11	6,5	6,8
12	7,5	9,9
13	7,1	9,6
14	8,3	10,8
15	5,6	8,9
16	4,5	7,0
17	6,1	8,0
18	3,0	2,5
19	6,9	9,2
20	6,5	6,9
21	4,1	4,3
22	4,1	4,4
23	4,2	6,0
24	4,1	7,5
25	5,6	8,9

С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском валовой продукции произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав пять групп заводов с равными интервалами. По каждой группе и совокупности заводов посчитайте:

1) число заводов;

2) среднегодовую стоимость основных производственных фондов – всего и в среднем на один завод.

3) стоимость валовой продукции всего и в среднем на один завод;

4) размер валовой продукции на один рубль основных производственных фондов (фондоотдачу).

Результаты представьте в виде групповой таблицы. Напишите краткие выводы.

Задача 2

Имеются следующие данные о заработной плате рабочих по цехам завода за два месяца.

Номер цеха	январь			февраль
Номер цеха	Средняя заработная плата, руб.	Фонд заработной платы, руб.	Средняя заработная плата, руб.		Численность рабочих, чел.
1	4800	595200	4850		120
2	5200	499200	5000		105

Вычислите среднюю месячную заработную плату рабочих по заводу:

1) за январь;

2) за февраль.

Дайте характеристику динамике средней заработной платы рабочих по

каждому цеху и в целом по заводу.

Укажите, какой вид средней надо применять для вычисления этих показателей.

Задача 3

В целях изучения стажа рабочих завода проведена пятипроцентная бесповторная выборка, в результате которой получено следующее распределение рабочих по стажу работы:

Стаж, число лет	Число рабочих, чел
До 6 6 – 12 12 – 18 18 – 24 свыше 24	15 25 35 15 6

На основе этих данных вычислите:

1) средний стаж рабочих завода;

2) средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение;

3) коэффициент вариации;

4) с вероятностью 0,997 предельную ошибку выбранной средней, возможные границы, в которых ожидается средний стаж рабочих завода;

5) с вероятностью 0,954 предельную ошибку выборочной доли и границы удельного веса числа рабочих со стажем работы от 6 до 12 лет.

Задача 4

Имеются данные о полугодовой динамике поставки шерстяных тканей в розничную сеть области, млн. руб.:

Для анализа представленного динамического ряда определите:

1) цепной абсолютный прирост, темп роста и темп прироста.

2) определите среднемесячный темп роста поставки шерстяных тканей. Сделайте выводы.

3) в целях анализа внутригодовой динамики и выявления общей тенденции развития определите индекс сезонности. Представьте графически сезонные волны развития данных явлений по месяцам.

Месяцы	Объем поставки
Январь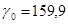
Февраль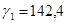
Март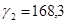
Апрель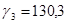
Май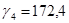
июнь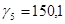

Задача 5

Остатки вкладов в сберегательных банках района одной из областей за первое полугодие характеризуются следующими данными, млн. руб.:

На 1 января – 10,3

На 1 февраля – 10,5

На 1 марта – 10,6

На 1 апреля – 10,8

На 1 мая – 11,3

На 1 июня – 11,6

На 1 июля – 11,8

Вычислите средний остаток вкладов:

1. за 1 квартал;

2. за 2 квартал;

3. за полугодие.

Поясните, почему методы расчета средних уровней рядов динамики в задачах 4, 5 различны.

Задача 6

Динамика средних цен и объема продажи на рынках города характеризуется следующими данными:

На основании имеющихся данных вычислите:

1. для рынка №1 (по двум видам товаров вместе):

а)общий индекс товарооборота;

б)общий индекс цен;

в)общий индекс физического объема товарооборота.

Определите в отчетном периоде прирост товарооборота и разложите по

факторам (за счет изменения цен и объема продажи товаров).

Покажите взаимосвязь между исчисленными индексами:

Наименование товара	Продано товара, единиц		Средняя цена за единицу
Наименование товара	Базисный период	Отчетный период	Базисный период	Отчетный период
Рынок №1
Молоко, л	600	550	10,5	12,5
Творог, кг	450	520	78	82
Рынок №2
Молоко, л	700	1000	10,0	12,9

2. Для двух рынков вместе (по молоку):

а)индекс цен переменного состава;

б)индекс постоянного состава;

в)индекс влияния изменения структуры объема продаж молока на динамику средней цены.

Объясните разницу между величинами индексов постоянного и переменного состава.

Задача 7

Имеются следующие данные о товарообороте магазина :

Товарная группа	Продано товаров в фактических ценах, тыс. руб.		Изменение цен в отчетном периоде по сравнению с базисным, %
Товарная группа	Базисный период	Отчетный период	Изменение цен в отчетном периоде по сравнению с базисным, %
Хлеб и хлебобулочные изделия	120,5	211,2	+4
Кондитерские изделия	30,4	54,6	- 3

Вычислите:

1) общий индекс товарооборота в фактических ценах;

2) общий индекс цен и сумму экономии от изменения цен, полученную населением в отчетном периоде при покупке товаров в данном магазине;

3) общий индекс физического объема товарооборота, используя взаимосвязь индексов.

Задача 8

Для изучения тесноты связи между выпуском валовой продукции на один завод (результативный признак - y) и оснащенностью заводов основными производственными фондами (факторный признак - х) по данным задачи 1 вычислите коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значение.

ВАРИАНТ ВТОРОЙ

Задача 1

Имеются следующие отчетные данные 25 заводов одной из отраслей промышленности:

Номер завода	Среднегодовая стоимость основных производственных фондов, млн. руб.	Валовая продукция в сопоставимых ценах, млн. руб.
1	3,4	3,5
2	3,1	3,3
3	3,5	3,5
4	4,1	4,5
5	5,8	7,5
6	5,2	6,9
7	3,8	4,3
8	4,1	5,9
9	5,6	4,8
10	4,5	5,8
11	4,2	4,6
12	6,1	8,4
13	6,5	7,3
14	2,0	2,1
15	6,4	7,8
16	4,0	4,2
17	8,0	10,6
18	5,1	5,8
19	4,9	5,3
20	4,3	4,9
21	5,8	6,0
22	7,2	10,4
23	6,6	6,9
24	3,0	3,5
25	6,7	7,2

5) число заводов;

6) среднегодовую стоимость основных производственных фондов – всего и в среднем на один завод.

7) Стоимость валовой продукции всего и в среднем на один завод;

8) Размер валовой продукции на один рубль основных производственных фондов (фондоотдачу).

Результаты представьте в виде групповой таблицы. Напишите краткие выводы.

Задача 2

Имеются следующие данные по зерновым культурам колхоза:

Культура	В отчетном периоде		План на предстоящий период
Культура	Урожайность, ц/га	Валовой сбор, ц	Урожайность, ц/га	Посевная площадь, га
Пшеница	21,0	63000	23,0	3300
Ячмень	19,0	38000	20,0	1800

Вычислите среднюю урожайность зерновых культур по колхозу:

1) в отчетном периоде;

2) в планируемом периоде.

Укажите, какой вид средней надо применить для вычисления этих показателей и какие изменения урожайности предусмотрены в плане на предстоящий период.

Задача 3

В целях изучения норм расходования сырья при изготовлении продукции на заводе проведена десятипроцентная механическая выборка, в результате которой получено следующее распределение изделий по массе:

Масса изделия, г	Число изделий, шт.
До 20 20 –21 21 –22 22 - 23 свыше 23	10 20 50 15 5

На основе этих данных вычислите:

1) среднюю массу изделия;

2) средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение;

3) коэффициент вариации;

4) с вероятностью 0,954 предельную ошибку выборочной средней, возможные границы, в которых ожидается средняя масса изделий всей партии изготовленных изделий;

5) с вероятностью 0,954 предельную ошибку выборочной доли и границы удельного веса изделий с массой веса от 20 до 23 г.

Задача 4

Субсидии, полученные населением крупного города, характеризуются следующими данными:

Для анализа динамики субсидий, полученных населением за 1998-2004 гг., вычислите:

1) абсолютные приросты, темпы прироста по годам. Полученные данные представьте в таблице.

2) среднегодовой уровень субсидий.

3) среднегодовой абсолютный прирост субсидий.

4) среднегодовые темпы роста субсидий с 1998 по 2004 гг.

Изобразите динамику субсидий, полученных населением за 1998-2004 гг. на графике.

Год	Субсидии, млн. руб.
1998	190,0
1999	211,6
2000	242,2
2001	268,6
2002	284,8
2003	300,7
2004	306,5

Задача 5

Имеются следующие данные о товарных запасах торгового дома в третьем квартале, млн. руб.

Группа товаров	На 1 июля	На 1 августа	На 1 сентября	На 1 октября
Продовольственные товары	1,5	1,4	1,5	1,8
Непродовольственные товары	3,5	3,8	3,7	3,4

Вычислите среднеквартальный остаток:

1) продовольственных товаров;

2) непродовольственных товаров;

3) по обеим товарным группам вместе.

Поясните, почему методы расчета средних уровней рядов динамики в задачах 4, 5 различны.

Задача 6

Динамика себестоимости и объема производства продукции характеризуется следующими данными:

Вид продукции	Выработано продукции, тыс.шт.		Себестоимость единицы продукции, тыс. руб.
Вид продукции	Базисный период	Отчетный период	Базисный период	Отчетный период
Ззавод №1
МП - 25	4,5	5,0	5,0	4,8
ММ - 29	3,2	3,0	8,0	8,2
Завод №2
МП - 25	10,6	10,0	7,0	6,6

На основании имеющихся данных вычислите:

1. для завода №1 (по двум видам продукции вместе):

а)общий индекс затрат на производство продукции;

б)общий индекс себестоимости продукции;

в)общий индекс физического объема производства продукции.

Определите в отчетном периоде изменение суммы затрат на производство продукции разложите по факторам (за счет изменения себестоимости и объема выработанной продукции).

Покажите взаимосвязь между исчисленными индексами:

2. Для двух заводов вместе (по продукции МП - 25):

а)индекс себестоимости переменного состава;

б)индекс себестоимости постоянного состава;

в)индекс влияния изменения структуры производства продукции на динамику средней себестоимости.

Объясните разницу между величинами индексов постоянного и переменного состава.

Задача 7

Имеются следующие данные о товарообороте магазина :

Товарная группа	Продано товаров в фактических ценах, тыс. руб.
Товарная группа	3 квартал	4 квартал
Мясо и мясопродукты	136,8	150,4
Молочные продукты	261,2	253,6

В 4 квартале по сравнению с третьим кварталом цены на мясо и мясные продукты повысились в среднем на 5%, а на молочные остались без изменения.

Вычислите:

4) общий индекс товарооборота в фактических ценах;

5) общий индекс цен;

6) общий индекс физического объема товарооборота, используя взаимосвязь индексов.

Задача 8

ВАРИАНТ ТРЕТИЙ

Задача 1

Имеются следующие отчетные данные 24 заводов одной из отраслей промышленности:

Номер завода	Среднегодовая стоимость основных производственных фондов, млн. руб.	Валовая продукция в сопоставимых ценах, млн. руб.
1	1,6	1,5
2	3,9	4,2
3	3,3	4,5
4	4,9	4,4
5	3,0	2,0
6	5,1	4,2
7	3,1	4,0
8	0,5	0,4
9	3,1	3,6
10	5,6	7,9
11	3,5	3,0
12	0,9	0,6
13	1,0	1,1
14	7,0	7,5
15	4,5	5,6
16	8,1	7,6
17	6,3	6,0
18	5,5	8,4
19	6,6	6,5
20	1,0	0,9
21	4,7	4,5
22	2,7	2,3
23	2,9	3,2
24	6,8	6,9

1) число заводов;

2) среднегодовую стоимость основных производственных фондов – всего и в среднем на один завод.

3) стоимость валовой продукции всего и в среднем на один завод;

4) размер валовой продукции на один рубль основных производственных фондов (фондоотдачу).

Результаты представьте в виде групповой таблицы. Напишите краткие выводы.

Задача 2

Имеются следующие данные о квалификации рабочих двух бригад:

№ бригады

Число рабочих

Уровень квалификации каждого рабочего бригады (тарифный разряд)

4; 3; 2; 4; 5; 6; 4; 3; 4; 3; 5; 4;

3; 5; 6: 5; 4; 3; 2: 3; 3; 4;

Определить средний уровень квалификации рабочих каждой бригады и двух бригад вместе.

Укажите, какой вид средней надо применять для вычисления этих показателей.

Задача 3

С целью изучения обеспеченности населения города предприятиями общественного питания проведена пятипроцентная механическая выборка, в результате которой получено следующие распределение предприятий общепита по числу посадочных мест:

Группы предприятий по числу посадочных мест, ед.	Число предприятий, ед.
До 16 16 –32 32 –48 48 –64 свыше 64	15 20 25 8 5

На основе этих данных вычислите:

1) среднее число посадочных мест на одно предприятие;

2) средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение;

3) коэффициент вариации;

4) с вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса числа предприятий с числом посадочных мест от 48 до 64.

Задача 4

Имеются данные о полугодовой динамике поставки бытовой техники в розничную сеть области, млн. руб.:

Месяцы	Отчетный период
Июль	132,4
Август	181,3
Сентябрь	127,8
Октябрь	119,4
Ноябрь	201,3
Декабрь	98,9

Для анализа представленного динамического ряда определите:

1. Цепной и базисный абсолютный прирост, темп роста и темп прироста.

2. Определите среднемесячный темп роста поставки тканей. Сделайте выводы.

3. В целях анализа внутригодовой динамики и выявления общей тенденции развития определите индекс сезонности. Представьте графически сезонные волны развития данных явлений по месяцам.

Задача 5

Имеются следующие данные об остатках товаров в розничном торговом предприятии:

	1 января	1 февраля	1 марта	1 апреля	1 мая	1 июня	1 июля
Остатки товара на начало месяца, тыс. руб.	50,2	61,4	63,6	72,8	61,6	58,8	62,0

Вычислите среднемесячные остатки товаров:

1. за 1 квартал;

2. за 2 квартал;

3. за полугодие.

Поясните, почему методы расчета средних уровней рядов динамики в задачах 4, 5 различны.

Задача 6

Динамика себестоимости и объема производства продукции характеризуется следующими данными:

Вид продукции	Выработано продукции, ед.		Себестоимость единицы продукции, тыс. руб.
Вид продукции	Базисный период	Отчетный период	Базисный период	Отчетный период
Завод №1
БМ – 40	2500	3000	14,0	13,0
АН - 50	5000	6000	18,0	17,0
Завод №2
БМ - 40	4000	5000	16,0	15,0

На основании имеющихся данных вычислите:

1. для завода №1 (по двум видам продукции вместе):

а)общий индекс затрат на производство продукции;

б)общий индекс себестоимости продукции;

в)общий индекс физического объема производства продукции.

Покажите взаимосвязь между исчисленными индексами:

2. Для двух заводов вместе (по продукции БМ – 40):

а)индекс себестоимости переменного состава;

б)индекс себестоимости постоянного состава;

в)индекс влияния изменения структуры производства продукции на динамику средней себестоимости.

Объясните разницу между величинами индексов постоянного и переменного состава.

Задача 7

Имеются следующие данные о товарообороте магазина

Товарная группа	Продано товаров в фактических ценах, тыс. руб.
Товарная группа	Базисный год	Отчетный год
Одежда, белье, ткани	1250,4	1480,2
Обувь кожаная	890,8	720,6

В отчетном годе по сравнению с базисным годом цены на одежду, белье, ткани повысились в среднем на 10%, а на кожаную обувь – на 8%.

Вычислите:

1. общий индекс товарооборота в фактических ценах;

2. общий индекс цен;

3. общий индекс физического объема товарооборота, используя взаимосвязь индексов.

4. Разложите по факторам прирост товарооборота магазина по данным товарным группам (за счет изменение цен и изменения количества проданных товаров).

Задача 8

ВАРИАНТ ЧЕТВЕРТЫЙ

Задача 1

Имеются следующие отчетные данные 25 заводов одной из отраслей промышленности:

Номер завода	Среднегодовая стоимость основных производственных фондов, млн. руб.	Валовая продукция в сопоставимых ценах, млн. руб.
1	4,0	4,2
2	8,0	10,4
3	5,1	5,8
4	4,9	5,3
5	6,3	8,0
6	7,5	9,4
7	6,6	11,2
8	3,3	3,4
9	6,7	7,0
10	3,4	2,0
11	3,3	3,3
12	3,9	5,4
13	4,1	5,0
14	5,9	7,0
15	6,4	7,9
16	3,9	6,4
17	5,6	4,6
18	3,5	4,1
19	3,0	3,8
20	5,4	8,5
21	2,0	1,8
22	4,5	4,6
23	4,8	5,2
24	5,9	9,0
25	7,2	8,6

С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском валовой продукции произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав четыре группы заводов с равными интервалами. По каждой группе и совокупности заводов посчитайте:

1) число заводов;

2) среднегодовую стоимость основных производственных фондов – всего и в среднем на один завод.

3) стоимость валовой продукции всего и в среднем на один завод;

4) размер валовой продукции на один рубль основных производственных фондов (фондоотдачу).

Результаты представьте в виде групповой таблицы. Напишите краткие выводы.

Задача 2

Имеются следующие данные о среднедневном товарообороте продавцов магазинов розничной торговой сети:

Номер магазина	Торговый дом № 1		Торговый дом №2
Номер магазина	Средний товарооборот продавца, руб.	Численность продавцов, чел.	Средний товарооборот продавца, руб.	Весь товарооборот, руб.
1.	16000	54	12500	930000
2.	18000	40	14000	1615000

Вычислите средний дневной товарооборот продавца:

1) по торговому дому №1.

2) по торговому дому № 2.

Укажите, в каком торге выше среднедневной товарооборот одного продавца и какой вид средней надо применить для вычисления этих показателей.

Задача 3

В целях изучения затрат времени на изготовление одной детали рабочими завода проведена десятипроцентная случайная бесповторная выборка, в результате которой получено следующее распределение деталей по затратам времени:

Затраты времени за одну деталь, мин.	Число изделий, шт.
До 10 10-12 12-14 14-16 16 и более	10 20 50 15 5

На основе этих данных вычислите:

1) средние затраты времени на изготовление одной детали;

2) средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение;

3) коэффициент вариации;

4) с вероятностью 0,954 предельную ошибку выборочной средней, возможные границы, в которых ожидается средние затраты времени на изготовление одной детали на заводе;

5) с вероятностью 0,954 предельную ошибку выборочной доли и границы удельного веса числа деталей с затратами времени на их изготовление от 10 до 12 минут.

Задача 4

Урожайность овощей в области (по всем категориям хозяйств) характеризуется следующими данными:

Для анализа данного ряда динамики, вычислите:

1) абсолютные приросты, темпы роста, темпы прироста (цепные). Полученные показатели представьте в таблице.

2) среднегодовую урожайность овощей.

3) базисный темп роста с помощью взаимосвязи цепных темпов роста.

4) среднегодовой темп роста и прироста.

Год	Средняя урожайность, ц / га
1998	150
1999	154
2000	162
2001	156
2002	180
2003	172

Изобразите урожайность овощей на графике. Сделайте выводы.

Задача 5

Имеются следующие данные о товарных запасах по одной из торговых организациях, млн. руб.:

Группа товаров	Запасы товаров
	Базисный год		Отчетный год		Следующий год
	На 01.01	На 01.07	На 01.01	На 01.07	На 01.01
Продовольственные товары	8,0	9,2	7,8	12,4	13,2
Непродовольственные товары	24,0	29,0	26,2	32,6	26,4

Вычислите средние товарные запасы в базисном и отчетном году:

1.по продовольственным товарам;

2. по непродовольственным товарам;

3. по обеим товарным группам вместе.

Поясните, почему методы расчета средних уровней рядов динамики в задачах 4, 5 различны.

Задача 6

Динамика себестоимости и объема производства продукции заводов характеризуется следующими данными:

Вид продукции	Выработано продукции, тыс.ед.		Себестоимость единицы продукции, тыс. руб.
Вид продукции	Базисный период	Отчетный период	Базисный период	Отчетный период
Завод №1
АМ – 45	8,5	6,5	2,9	2,6
ТС – 37	6,4	6,4	3,3	3,5
Завод №2
АМ – 45	10,0	12,0	4,0	4,2

На основании имеющихся данных вычислите:

1. Для завода №1 (по двум видам продукции вместе):

а)общий индекс затрат на производство продукции;

б)общий индекс себестоимости продукции;

в)общий индекс физического объема производства продукции.

Покажите взаимосвязь между исчисленными индексами:

3. Для двух заводов вместе (по продукции АМ – 45):

а)индекс себестоимости переменного состава;

б)индекс себестоимости постоянного состава;

в)индекс влияния изменения структуры производства продукции на динамику средней себестоимости.

Объясните разницу между величинами индексов постоянного и переменного состава.

Задача 7

Имеются следующие данные о товарообороте магазина :

Товарная группа	Продано товаров в фактических ценах, тыс. руб.
Товарная группа	Базисный год	Отчетный год
Трикотажные изделия	310,1	361,1
Чулочно-носочные изделия	150,7	196,3

В отчетном году по сравнению с базисным годом количество проданных товаров увеличились по трикотажным изделиям на 5%, а по чулочно-носочным – на 15%.

Вычислите:

1) общий индекс товарооборота в фактических ценах;

2) общий индекс физического объема (количества) продажи товаров;

3) общий индекс цен, используя взаимосвязь индексов.

Как повлияло изменение цен на величину товарооборота ?

Задача 8

ВАРИАНТ ПЯТЫЙ

Задача 1

Имеются следующие отчетные данные 23 заводов одной из отраслей промышленности:

Номер завода	Среднегодовая стоимость основных производственных фондов, млн. руб.	Валовая продукция в сопоставимых ценах, млн. руб.
1	12,7	16,6
2	6,9	7,6
3	7,3	11,2
4	2,9	3,2
5	4,5	4,9
6	12,8	15,0
7	7,8	12,0
8	0,8	0,7
9	4,1	5,3
10	4,3	4,8
11	5,5	5,7
12	4,3	4,8
13	9,1	10,9
14	1,4	1,2
15	7,6	8,6
16	3,6	3,6
17	4,4	6,7
18	6,9	8,4
19	4,6	6,9
20	5,8	6,7
21	11,7	17,9
22	7,4	10,4
23	10,9	15,5
24	3,9	6,3
25	11,0	14,1

С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском валовой продукции произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав четыре группы заводов с равными интервалами. По каждой группе и совокупности заводов посчитайте:

1) число заводов;

2) среднегодовую стоимость основных производственных фондов – всего и в среднем на один завод.

3) стоимость валовой продукции всего и в среднем на один завод;

4) размер валовой продукции на один рубль основных производственных фондов (фондоотдачу).

Результаты представьте в виде групповой таблицы. Напишите краткие выводы.

Задача 2

Имеются следующие данные о численности рабочих в бригадах в двух отраслях народного хозяйства двух областей за отчетный год:

Область	Промышленность		Строительство
Область	Численность рабочих в одной бригаде, чел.	Число бригад, ед.	Численность рабочих в одной бригаде, чел.	Общая численность рабочих всех бригад, чел.
А	15	1200	19	9500
Б	18	1500	23	18400

Вычислите среднюю численность рабочих одной бригады:

1)в промышленности;

2)в строительстве.

Укажите, какой вид средней надо применить для вычисления этих показателей. Сравните полученные средние.

Задача 3

В целях изучения дневной выработки рабочими завода проведена десятипроцентная случайная бесповторная выборка, в результате которой получено следующее распределение рабочих:

Группы рабочих с дневной выработкой изделий, шт.	Число рабочих, чел..
До 20 20-30 30-40 40-50 свыше 50	5 10 40 22 8

На основе этих данных вычислите:

1) среднедневную выработку изделий;

2) средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение;

3) коэффициент вариации;

4) с вероятностью 0,954 предельную ошибку выборочной средней, возможные границы, в которых ожидается среднедневная выработка изделий всеми рабочими завода;

5) с вероятностью 0,954 предельную ошибку выборочной доли и границы удельного веса рабочих, с дневной выработкой от 40 до 50 изделий.

Задача 4

Производство продукции предприятия характеризуется следующими данными:

Для анализа данного ряда динамики, вычислите:

1) среднемесячное производство продукции.

2) базисный темп роста с помощью взаимосвязи цепных темпов роста.

3) среднемесячный темп роста и прироста. Результаты представьте в таблице.

Месяцы	Производство продукции, тыс. руб.
Январь	1100
Февраль	1200
Март	1300
Апрель	1350
Май	1500
Июнь	1600

Изобразите динамику производства продукции на графике. Сделайте выводы.

Задача 5

Имеются следующие данные о товарных запасах непродовольственных товаров

торговой организации, млн. руб.:

На 1 января – 4,5

На 1 апреля – 4,6

На 1 июля – 4,8

На 1 октября – 4,5

На 1 января следующего года – 4,2

Вычислите средние товарные запасы торговой организации:

1) За 1 полугодие;

2) за 2 полугодие;

3) за год.

Поясните, почему методы расчета средних уровней рядов динамики в задачах 4, 5 различны.

Задача 6

Динамика себестоимости и объема производства продукции характеризуется следующими данными:

Вид продукции	Выработано продукции, тыс.ед.		Себестоимость единицы продукции, тыс. руб.
Вид продукции	Базисный период	Отчетный период	Базисный период	Отчетный период
Завод №1
ЛР – 34	2,7	2,7	3,2	3,1
АВ - 50	4,0	4,8	1,5	1,5
Завод №2
АВ - 50	2,0	1,2	1,4	1,3

На основании имеющихся данных вычислите:

1. Для завода №1 (по двум видам продукции вместе):

а)общий индекс затрат на производство продукции;

б)общий индекс себестоимости продукции;

в)общий индекс физического объема производства продукции.

Определите в отчетном периоде изменение суммы затрат на производство продукции (за счет изменения себестоимости и объема выработанной продукции).

Покажите взаимосвязь между исчисленными индексами:

2. Для двух заводов вместе (по продукции АВ - 50):

а)индекс себестоимости переменного состава;

б)индекс себестоимости постоянного состава;

в)индекс влияния изменения структуры производства продукции на динамику средней себестоимости.

Объясните разницу между величинами индексов постоянного и переменного состава.

Задача 7

Имеются следующие данные о товарообороте магазина :

Товарная группа	Продано товаров в фактических ценах, тыс. руб.
Товарная группа	Базисный год	Отчетный год
Картофель	562,5	670,9
Фрукты и цитрусовые	348,2	451,6

В отчетном году по сравнению с базисным годом цены на картофель повысились на 7%, а на фрукты и цитрусовые остались без именения.

Вычислите:

1) общий индекс товарооборота в фактических ценах;

2) общий индекс цен и сумму дополнительных расходов населения вследствие изменения цен в отчетном году при покупке товаров в данном магазине;

3)общий индекс физического объема товарооборота, используя взаимосвязь индексов.

Задача 8

РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ

1.1 Имеются следующие данные по заработной плате водителей за сентябрь:

Табельный номер водителя	Класс водителя	Процент выполнения норм выработки	Заработная плата за месяц
1 2 3 4 5 6 7 8 9 10 11 12	I II II I II I I II I II I I	110,2 102,0 111,0 107,9 106,4 109,0 115,0 112,2 105,0 107,4 112,5 108,6	2100,3 1600,8 1970,7 2050,2 1740,5 1985,4 2300,8 2015,7 1790,2 1700,7 2280,2 2170,1

Для выявления зависимости заработной платы водителей от уровня квалификации и процента выполнения норм выработки произвести аналитическую группировку. Интервалы группировки водителей по проценту выполнения норм выработки разработать самостоятельно. На основе выполненной группировки построить комбинационную таблицу. Сформулировать вывод.

Решение

Для решения задачи необходимо произвести группировку водителей по двум признакам-факторам: сначала - на группы по квалификации, затем внутри каждой группы - на подгруппы по проценту выполнения норм выработки.

По проценту выполнения норм выработки принимаются две подгруппы: 1) водители, выполняющие норму от 100 до 110%; 2) водители, выполняющие норму на 110% и выше.

Результаты группировки представлены во вспомогательной табл. 1.1.

На основе вспомогательной таблицы по каждой подгруппе определяют численность и итог признака (общую сумму заработной платы), результаты оформляют в виде комбинационной таблицы (табл. 1.2).

Таблица 1.1

Вспомогательная таблица

группы водителей по уровню классификации	водители II класса		водители I класса
Подгруппы водителей по проценту выполнения норм выработки	100 - 110	110 и выше	100 - 110	110 и выше
Табельный номер водителя	2;5;10	3;8	4;6;9;12	1;7;11
Заработная плата за месяц, руб	1600,8 1740,5 1700,7	1970,7 2015,7	2050,2 1985,4 1790,2 2170,1	2100,3 2300,8 2280,2

Таблица 1.2

Зависимость заработной платы водителей от классификации и процента выполнения норм выработки

группы водителей по уровню классификации	Подгруппы водителей по проценту выполнения норм выработки	число водителей	общая сумма заработной платы, руб.	средняя заработная плата одного водителя, руб.	изменение средней заработной платы по сравнению с низшей подгруппой, %
II класс	100 – 110 110 и выше	3 2	5042,0 3986,4	1680,7 1993,2	100,0 118,6
итого по группе		5	9028,4	1805,7	-
I класс	100 – 110 110 и выше	4 3	7995,9 6681,3	1999,0 2227,1	118,9 132,5
итого по группе		7	14677,2	2096,7	-
всего		12	23705,6	1975,5	-

Из данных табл. 1.2 следует, что с ростом квалификации водителей и процента выполнения норм выработки увеличивается заработная плата. Так, заработная плата водителей I класса, выполняющих норму выработки на 110% и выше, на 32,5% превышает заработную плату водителей II класса, выполняющих нрр-му от 100 до 110%.

Средние величины.

Средней величиной называется обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени.

Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.

При использовании средних в практической работе и научных исследованиях необходимо иметь в виду, что за средним показателем скрываются особенности различных частей изучаемой совокупности, поэтому общие средние для однородной совокупности должны дополняться групповыми средними, характеризующими части совокупности.

В экономических исследованиях и плановых расчетах применяются две категории средних:

• степенные средние;

• структурные средние.

К категории степенных средних относятся: средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя геометрическая. Величины, для которых исчисляется средняя, обозначаются буквой хi. Средняя обозначается через x. Такой способ обозначения указывает на происхождение средней из конкретных величин. Черта вверху символизирует процесс осреднения индивидуальных значений. Частота - повторяемость индивидуальных значений признака - обозначается буквой f

Формулы средних величин могут быть получены на основе степенной средней, для которой определяющей функцией является уравнение

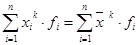
откуда

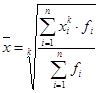
В дальнейшем при написании формул средних подстрочные значки I, п использоваться не будут, но подразумевается, что суммируются все произведения х, /,.

В зависимости от степени 1с получаются различные виды средних величин, их формулы представлены в табл. 2.1.

Как видно из данных табл. 2.1, взвешенные средние учитывают, что отдельные варианты значений признака имеют различную численность, поэтому каждый вариант «взвешивают» по своей частоте, т. е. умножают на нее. Частоты/при этом называются статистическими весами или просто весами средней.

Однако необходимо учитывать, что статистический вес - понятие более широкое, чем частота. В качестве веса могут применяться какие-либо другие величины (в табл. 2.1 они обозначены буквой и'). Например, при расчете средней продолжительности рабочего дня по предприятию единственно правильным будет взвешивание по количеству отработанных человеко-дней. Частоты отдельных вариантов могут быть выражены не только абсолютными величинами, но и относительными - частостямн.

Величины степенных средних, рассчитанных на основе одних и тех же индивидуальных значений признака при различных значениях степени (k), не одинаковы. Чем выше степень k средней, тем больше величина самой средней.

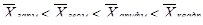
Таблица 2.1 Формулы различных видов степенных средних величин

Значе-ние x	Наименование средней	формула средней
Значе-ние x	Наименование средней	простая	взвешенная
-1	Гармоническая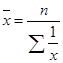
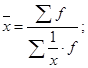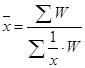
0	Геометрическая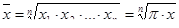
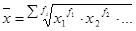
1	Арифметическая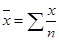
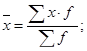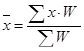
2	Квадратическая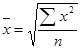

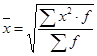
Средняя арифметическая и средняя гармоническая наиболее распространенные виды средней, получившие широкое применение в плановых расчетах, при расчете общей средней из средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок. Выбор средней арифметической и средней гармонической определяется характером имеющейся в распоряжении исследователя информации.

Средняя квадратическая применяется для расчета среднего квадратического отклонения (а), являющегося показателем вариации признаков, а также в технике (например, при сооружении трубопроводов).

Средняя геометрическая (простая) используется при вычислении среднего коэффициента роста (темпа) в рядах динамики.

Структурные средние - мода и медиана - в отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решении ряда практических задач.

Модой называется значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду).

Медианой называется значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.

Ранжированный ряд - ряд, расположенный в порядке возрастания или убывания значений признака.

Для определения медианы сначала определяют ее место в ряду, используя формулу

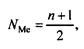
Если ряд состоит из четного числа членов, то за медиану условно принимают среднюю арифметическую их двух срединных значений.

Применяется мода при экспертных оценках, при определении наиболее ходовых размеров обуви, одежды, что учитывается при планировании их производства. Медиана используется при статистическом контроле качества продукции и технологического процесса на промышленных предприятиях; при изучении распределения семей по величине дохода и др. Мода и медиана имеют преимущество перед средней арифметической для ряда распределения с открытыми интервалами.

РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ

3.2. Имеются следующие данные о возрастном составе рабочих цеха (лет): 18; 38; 28; 29; 26; 38; 34; 22; 28; 30; 22; 23; 35; 33; 27; 24; 30; 32; 28; 25; 29; 26; 31; 24; 29; 27; 32; 25; 29; 29.

Для анализа распределения рабочих цеха по возрасту требуется: 1) построить интервальный ряд распределения; 2) дать графическое изображение ряда; 3) исчислить показатели центра распределения, показатели вариации и формы распределения. Сформулировать вывод.

Решение \. Величина интервала группировки определяется по формуле

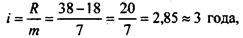
Интервальный ряд распределения

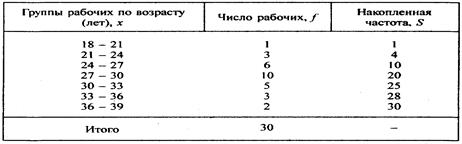
2. Графически интервальный вариационный ряд может быть представлен в виде гистограммы, полигона, кумуляты.

Гистограмма строится в прямоугольной системе координат. По оси абсцисс откладывают интервалы значений вариационного признака, причем число интервалов целесообразно увеличить на два4ло одному в начале и в конце имеющегося ряда) для удобства преобразования гистограммы в полигон частот. На отрезках (интервалах) строятся прямоугольники, высота которых соответствует частоте.

Для преобразования гистограммы в полигон частот середины верхних сторон прямоугольников соединяют отрезками прямой, и две крайние точки прямоугольников замыкаются по оси абсцисс на середине интервалов, в которых частоты равны нулю.

На рис. 3.2 представлено графическое изображение построенного интервального вариационного ряда в виде гистограммы и полигона частот.

Как видно из графика, треугольники, относящиеся к площади гистограммы и к площади полигона, попарно равны между собой, и, следовательно, площадь гистограммы и площадь полигона данного вариационного ряда также совпадают.

На основе построенной гистограммы графически можно определить значение моды. Для этого правую вершину модального прямоугольника соединяют прямой с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника соединяют с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения. Мо = 28,3 года. На рис. 3.2 эти прямые

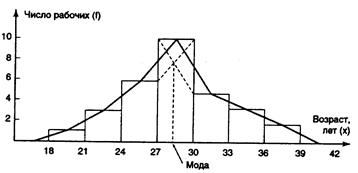
Рис. 3.2. Гистограмма и полигон распределения рабочих цеха по возрасту линии, соединяющие вершины прямоугольников, и перпендикуляр из точки их пересечения показаны пунктирной линией.

На рис. 3.3 представлена кумулятивная кривая (кумулята).

Кумулята может быть использована для графического определения медианы. Для этого последнюю ординату кумуляты делят пополам. Через полученную точку проводят прямую, параллельную оси дг, до пересечения ее с кумулятой. Из точки пересечения опускается перпендикуляр до оси абсцисс. Абсцисса точки пересечения является медианой. Линии, определяющие медиану, на рис. 3.3 показаны пунктирными линиями. Ме = 28,6 года.

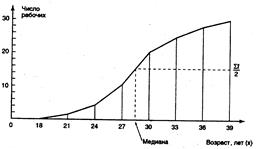
3. Расчет показателей центра распределения:

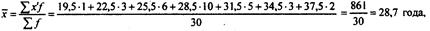
Для интервального вариационного ряда порядок расчета структурных средних следующий: сначала находят интервал, содержащий моду или медиану, а затем рассчитывают соответствующие значения названных показателей.

Модальным в данном распределении является интервал 27 -30 лет, так как наибольшее число рабочих {f = 10) находится в этом интервале. Значение моды определяется по формуле

Для расчета показателей вариации составляется вспомогательная таблица (табл. 3.4).

Таблица 3.4 Вспомогательная таблица для расчета показателей

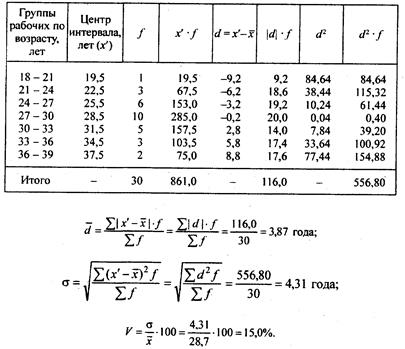
Следовательно, вариация возраста у рабочих данного цеха не является значительной, что подтверждает достаточную однородность совокупности.

Как видно на рис. 3.2, распределение рабочих по возрасту несимметрично, поэтому определяется показатель асимметрии:

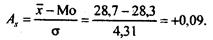
Следовательно, асимметрия правосторонняя, незначительная. При правосторонней асимметрии между показателями центра распределения существует соотношение

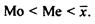
Для данного распределения это соотношение выполняется, т. е. 28, 33 < 28, 65 < 28, 70. При левосторонней асимметрии (Л, со знаком минус) соотношение между показателями центра распределения будет иметь вид:

Мо > Ме > х.

ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ

Понятие о выборочном наблюдении

Выборочное наблюдение при строгом соблюдении условий случайности и достаточно большой численности отобранных единиц репрезентативно (представительно); по результатам изучения определенной части единиц с достаточной для практики степенью точности можно судить о всей совокупности. Однако вычисленные по материалам выборочного наблюдения статистические показатели не будут точно совпадать с соответствующими характеристиками для всей совокупности (генеральной совокупности). Величина этих отклонений называется ошибкой наблюдения, которая складывается из ошибок двоякого рода: ошибки регистрации (точности) и ошибки репрезентативности.

Ошибки репрезентативности свойственны только несплошным наблюдениям. Они характеризуют размер расхождений между величинами показателя, полученного в выборочной и генеральной совокупности в условиях одинаковой точности единичных наблюдений. Ошибки репрезентативности могут быть систематическими и случайными. Систематические ошибки возникают при нарушении установленных правил отбора единиц. Случайные ошибки репрезентативности обязаны своим возникновением недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности.

Величина случайной ошибки определяет надежность данных выборочного наблюдения, их пригодность для суждения о генеральной совокупности. При помощи формул теории вероятностей можно рассчитать возможную максимальную случайную ошибку - вероятный (стохастический) предел ошибки.

Максимально возможная ошибка - это такая величина отклонения выборочной средней (доли) от генеральной, вероятность превышения которой вследствие случайных причин в условиях данной выборки очень мала.

Величина случайной ошибки репрезентативности зависит от:

• степени колеблемости изучаемого признака в генеральной совокупности;

• способа формирования выборочной совокупности;

• объема выборки.

По степени охвата единиц исследуемой совокупности различают большие и малые выборки.

По способу формирования выборочной совокупности различают следующие виды выборочного наблюдения: простая случайная (собственно случайная) выборка, расслоенная (типическая или районированная), серийная, механическая, комбинированная, ступенчатая, многофазная.

Принятые условные обозначения

Совокупность единиц, из которых производится отбор, принято называть генеральной совокупностью. Совокупность отобранных единиц из генеральной совокупности называется выборочной совокупностью.

N - объем генеральной совокупности (число входящих в нее единиц);

п - объем выборочной совокупности (число единиц, попавших в выборку);

х - генеральная средняя (среднее значение признака в генеральной совокупности);

х - выборочная средняя (среднее значение признака в выборочной совокупности);

р - генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности);

w - выборочная доля (доля единиц, обладающих данным признаком в выборочной совокупности);

ơ² - генеральная дисперсия (дисперсия признака в генеральной совокупности);

S² - выборочная дисперсия (дисперсия признака в выборочной совокупности);

ơ- среднее квадратическое отклонение признака в генеральной совокупности;

S - среднее квадратическое отклонение признака в выборочной совокупности.

Простая случайная выборка

При простой случайной выборке отбор единиц в выборочную совокупность производится непосредственно из всей массы единиц генеральной совокупности в форме случайного отбора, при котором каждой единице генеральной совокупности обеспечивается одинаковая вероятность (возможность) быть выбранной. Единица отбора совпадает с единицей наблюдения. Случайный отбор осуществляется путем применения жеребьевки (лотереи) или путем использования таблиц случайных чисел.

Случайный отбор может быть проведен в двух формах: в форме возвратной (повторной) выборки ив форме безвозвратной (бесповторной) выборки. При повторном отборе вероятность попадания каждой единицы генеральной совокупности остается постоянной, так как после отбора какой-то единицы она снова может быть выбранной. При бесповторном отборе выбранная единица не возвращается в генеральную совокупность и вероятность попадания отдельных единиц в выборку все время изменяется (для оставшихся единиц она возрастает).

Применение простой случайной повторной выборки на практике весьма ограниченно; обычно используется бесповторная выборка.

В табл. 4.1 приведены формулы расчета ошибок простой случайной выборки.

Формулы предельной ошибки позволяют решать задачи трех видов:

1. Определение пределов генеральных характеристик с

заданной степенью надежности (доверительной вероятностью) на основе показателей, полученных по данным выборки. Доверительные интервалы для генеральной средней –

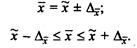
Доверительные интервалы для генеральной доли -

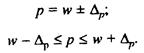
2. Определение доверительной вероятности того, что генеральная характеристика может отличаться от выборочной не более чем на определенную заданную величину.

Доверительная вероятность является функцией от t, определяемой по формуле

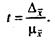
По величине t определяется доверительная вероятность (приложение 3).

3. Определение необходимого объема выборки, который с практической вероятностью обеспечивает заданную точность выборки.

В табл. 4.2 приведены формулы для расчета численности простой случайной выборки.

Таблица 4.2 Формулы для определения численности простой случайной

РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ

4.1. Из партии электроламп взята 20%-ная случайная бесповторная выборка для определения среднего веса спирали. Результаты выборки следующие:

Определить с вероятностью 0,95 доверительные пределы, в которых лежит средний вес спирали, для всей партии электроламп.

4.2. На заводе электроламп из партии продукции в количестве 16000 шт. ламп взято на выборку 1600 шт. (случайный, бесповторный отбор), из которых 40 шт. оказались бракованными.

Определить с вероятностью 0,997 пределы, в которых будет находиться процент брака для всей продукции

РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ

Задача 1. Выпуск продукции по заводу почвообрабатывающих машин за два квартала следующий:

Вид продукции	Выпуск, шт.		Отпускная цена за шт., тыс. д.е
	1 кв. (q0)	2 кв. (q1)	1 кв. (p0)	2 кв. (p1)
Плуги навесные 2500		2610 4,8 5,4
Плуги прицепные 3000		2950 7,1 7,6
Культиваторы навесные 3600		3700 5,0 5,7

Определить:

1) изменение (в %) выпуска каждого вида продукции, а также изменение выпуска продукции в целом по предприятию;

2) изменение цен (в %) по каждому виду продукции и среднее изменение цен по всему ассортименту продукции;

3) абсолютное изменение общей стоимости продукции, выделив из общей суммы изменение за счет изменения количества продукции и за счет изменения цен.

Решение

Для характеристики изменения выпуска продукции в целом по предприятию исчисляется агрегатный индекс физического объема продукции:

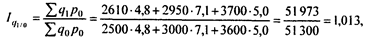
или 101,3%, т. е. в целом по предприятию выпуск продукции увеличился на 1,3%, в результате стоимость продукции увеличилась на 673 000 руб. (51 973 - 51 300).

Среднее изменение цен по всему ассортименту продукции определяется по формуле агрегатного индекса цен:

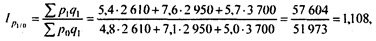
или 110,8%.

Таким образом, цены на продукцию предприятия повышены в среднем на 10,8%, за счет чего стоимость продукции повысилась на 5631 тыс. руб. (57 604-51 973).

3. Абсолютное изменение стоимости продукции определяется по формуле

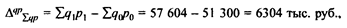
- абсолютное изменение стоимости продукции за счет изменения выпуска продукции

тыс. руб.;

- абсолютное изменение стоимости продукции за счет изменения цен;

тыс. руб;

что и соответствует ранее полученной цифре.

Задача 2. Определить, как изменились в среднем отпускные цены на продукцию, если количество произведенной продукции в отчетном периоде по сравнению с базисным увеличилось на 8,0%, а общая стоимость продукции уменьшилась на 5,0%.

Решение

Для определения индекса цен используется взаимосвязь между тремя индексами:

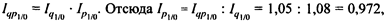
или 97,2%. Следовательно, отпускные цены на продукцию снижены в среднем на 2,8%.

6. ВОПРОСЫ К ЭКЗАМЕНУ (ЗАЧЕТУ) ПО СТАТИСТИКЕ

1. Современная организация статистики. Задачи органов статистики в условиях рыночных отношений.

2. Статистическое наблюдение. Основные организационные формы статистического наблюдения.

3. Виды статистического наблюдения.

4. Организация статистической отчетности. Специальные статистические наблюдения. Ошибки наблюдения.

5. Задачи группировок. Виды группировок: типологические, структурные, аналитические.

6. Группировочные признаки, их сущность и значение.

7. Важнейшие группировки и классификации, применяемые в статистике.

8. Ряды распределения. Их виды, назначение и использование.

9. Абсолютные величины и их значение в статистическом исследовании. Виды абсолютных величин, единицы измерения.

10.Виды относительных величин, способы их расчета и формы

выражения.

11.Виды средних и способы определения их величин.

12.Выборочное наблюдение - основные приема расчета ошибок.

13.Задачи статистического изучения вариации. Основные показатели

вариации.

14.Виды дисперсии. Правило сложения дисперсий.

15.Понятие о рядах динамики и их значение.

16.Основные правила построения рядов динамики.

17.Виды зависимостей между факторами. Показатели регрессии.

18.Аналитические модели зависимости между факторами.

19.Анализ рядов динамики.

20. Аналитические приемы обработки рядов динамики.

21.Понятие об индексах. Значение индексов в анализе социально-

экономических явлений.

22.Классификация индексов.

23.Индивидуальные и общие индексы.

24.Агрегатный индекс как основная форма общего индекса.

25.Средний арифметический и гармонический индексы.

26.Система взаимосвязей индексов.

27.Индексы постоянного, переменного состава и структурных

сдвигов.

28.Базисные и цепные индексы, их взаимосвязь.

Выборочное наблюдение

1. В АО «Прогресс» работает 3000 человек. Методом случайной бесповторной выборки обследовано 1000 человек, из которых 820 выполняли и перевыполняли дневную норму выработки.

Определить: 1) долю рабочих, не выполняющих норму выработки, по данным выборочного обследования; 2) долю всех рабочих акционерного общества, не выполняющих норму (с вероятностью 0,954).

а) 1)0,18 ;2)0,18 +/-0,02

б) 1) 2,2 ; 2) 2,22 +/- 0,03

в) 1)1,2; 2) 1,1 +/- 0,1

г) 1) 1,27; 2) 1,1 +/- 0,1

2. Из партии изготовленных изделий общим объемом 2000 единиц проверено посредством механической выборки 30% изделий, из которых бракованными оказались 12 изделий.

Определить: 1) долю бракованных изделий по данным выборки; 2) пределы, в которых находится процент бракованных изделий, для всей партии (с вероятностью 0,954).

а) 1)0,03 или 3% 2)3,0 +/- 0,96

б) 1)0,02 или 2% 2) 2,0 +/- 0,96

в) 1) 0,01 или 1% 2) 4,0 +/- 0,96

г) 1) 0,05 или 5% 2) 7,0 +/- 0,96

3. Объем выборки: 1) увеличился в 2 раза; 2) уменьшился в 2 раза.

Определить, как изменится ошибка простой случайной повторной выборки.

а) 1) уменьшение в 1,41 раза 2) уменьшение в 1,41 раза

б) 1) увеличение в 1,78 раза 2) уменьшение в 1,78 раза

в) 1) увеличение в 1,41 раза 2) увеличение в 1,41 раза

г) 1)уменьшение в 1,41 раза 2) увеличение в 1,41 раза

4. Сколько фирм необходимо проверить налоговой инспекции района, чтобы ошибка доли фирм, несвоевременно уплачивающих налоги, не превысила 5%? По данным предыдущей проверки, доля таких фирм составила 32%. Доверительную вероятность принять равной 0,954 (0,997).

а) 348; 783

б) 543; 765

в) 768; 432

г) 987; 254

5. Какова должна быть численность механической выборки для определения доли служащих, прошедших повышение квалификации по использованию вычислительной техники, чтобы с вероятностью 0,954 ошибка репрезентативности не превышала 10%? Общая численность служащих предприятия составляет 324 человека.

а) 67

б) 89

в) 99

г) 76

Ряды динамики

1. Удельный вес городского населения региона увеличился с 1 января 1999 г. по 1 января 2005 г. с 36,2 до 42,8%. Определить показатели динамики численности городского и сельского населения региона, если общая численность населения данного региона за этот период возросла на 8,4%.

а) численность городского население увеличилась на 28,8%, сельского снизилась на 2,8%

б) численность городского население уменьшилась на 28,8%, сельского увеличилась на 2,8%

в) численность городского население увеличилась на 30%, сельского снизилась на 4%

г) численность городского население уменьшилась на 30%, сельского увеличилась на 4%

2. Динамика объема реализации услуг коммунальных предприятий города в процентах к 1993 г. составила:

1994 г. - 108,0;

1995 г. - 110,5;

1996 г. - 125,0;

1997 г. - 153,2.

Определить: а) коэффициенты роста для 1996 и 1997 гг. по сравнению с 1995 г.; б) среднегодовой темп прироста за период 1993 - 1997 гг.

а) К_р = 1,154; К_р = 1,389; К_р = 2,1225; Т_n = 12,45%

б) К_р = 1,331; К_р = 5,387; К_р = 1,5643; Т_n = 17,25%

в) К_р = 1,131; К_р = 1,386; К_р = 1,1125; Т_n = 11,25%

г) К_р = 3,161; К_р = 2,376; К_р = 1,1025; Т_n = 10,35%

3. Стоимость основных средств на предприятии за отчетный год составила (млн руб.):

на 1 января - 4,8; на 1 апреля - 4,0; на 1 мая - 5,0; на 1 октября - 6,0;

на 1 января (следующего года) - 5,2

Определить среднегодовую стоимость основных средств предприятия и величину 1 % прироста за год.

а) у = 5,78 млн. руб; Т_n = 2,8%;D = 0,7 млн. руб.;А = 50,0 тыс. руб.

б) у = 5,17 млн. руб; Т_n = 2,02%;D = 0,1 млн. руб.;А = 49,5 тыс. руб.

в) у = 6,18 млн. руб; Т_n = 4,0%;D = 0,04 млн. руб.;А = 29,8 тыс. руб.

г) у = 4,45млн. руб; Т_n = 2,2%;D = 1,1 млн. руб.; А = 59,6 тыс. руб.

4. Остаток средств на расчетном счете предприятия составил на 1 января 2004 г. 180 тыс. руб.; 15 января поступило на расчетный счет 900 тыс. руб.; 22 января списано с расчетного счета 530 тыс. руб.; 27 января поступило на расчетный счет 380 тыс. руб. С 28 января до конца месяца остаток средств на расчетном счете не изменился.

Определить среднесуточный остаток средств на расчетном счете предприятия в январе.

а) у = 679,098

б) у = 898,988

в) у = 999,999

г) у = 563,871

Индексы и их использование

1. Определить, на сколько процентов изменилась стоимость продукции в отчетном году по сравнению с прошлым годом, если известно, что количество произведенной продукции в натуральном выражении уменьшилось на 2,5%, а отпускные цены на продукцию увеличились на 5,2%.

а) уменьшение на 5,9%

б) не изменилась

в) увеличение на 2,6%

г) уменьшение на 4,9%

2. Стоимость продукции в ценах соответствующих лет составила: в 2003 г. - 25 млн руб., в 2004 г. - 32,5 млн руб. Индекс цен в 2004 г. составил по сравнению с 2003 г. 115%. Производительность труда на одного работающего возросла за этот период со 120 до 144 тыс. руб. Определить индексы физического объема продукции, производительности труда и численности работающих.

а) 1,13; 1,20; 0,94

б) 0,89; 3,09; 0,98

в) 0,99; 0,88; 0,76

г) 1,76; 0,65; 1,34

3. В прошлом году металлургический завод выпустил чугуна на 5000 тыс. руб., стали - на 3 500, проката - на 2 100 тыс. руб. На отчетный год предусмотрено увеличение производства чугуна на 12,0%, стали - на 7,5, проката - на 3,2%.

Определить, на сколько процентов должно увеличиться производство продукции в целом по предприятию.

а) увеличение на 6,7%

б) уменьшение на 8,9%

в) увеличение на 8,8%

г) уменьшение на 7,6%

4. По машиностроительному предприятию объем выпущенной продукции во II квартале увеличился по сравнению с I кварталом на 10%, в III квартале по сравнению со II кварталом он снизился на 1,2%, а в IV квартале по сравнению с III кварталом объем выпущенной продукции увеличился на 12,5%.

Определить, как изменился объем выпущенной продукции на предприятии в IV квартале по сравнению с I кварталом.

а) увеличение на 76,9%

б) уменьшение на 89,9%

в) увеличение на 23,32%

г) увеличение на 22,27%

5. Товарооборот предприятия увеличился в отчетном году по сравнению с прошлым годом в 1,2 раза при снижении цен за этот же период в среднем на 5%. Как изменился объем реализованной товарной массы в отчетном году?

а) уменьшение на 33,1%

б) увеличение на 26,3%

в) увеличение на 55,1%

г) уменьшение на 11,5%

УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ.

ОСНОВНАЯ ЛИТЕРАТУРА

1. Елисеева И.И., Юзбашев М.М. Общая теория статистики.-М.: Финансы и статистика, 1996.

2. Статистика. Курс лекций/ Под ред. проф. В.Г. Ионина.— Новосибирск: изд-во НГАЭиУ,1996.

3. Теория статистики/ Под ред проф. Р.А. Шмойловой—-М.: Финансы и статистика, 2003г.

4. Спирин И.А., Башина О.Э. Общая теория статистики.-М.: Финансы и статистика, 2002

5. Ефимова М.Р., Петрова З.В. Общая теория статистики.-М.: Финансы и статистика, 1999.

6. Ефимова М.Р., Рябцев В.М. Общая теория статистики.—М.: Финансы и статистика, 1991.

7. Практикум по теории статистики/ Под ред проф. Р.А. Шмойловой—-М.: Финансы и статистика, 2003г.

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. Адамов В.Е. Факторный индексный анализ. Методология и проблемы—-М.: Статистика, 1977.

2. Аллен Р. Экономические индексы: Пер. с англ.—М.: Статистика, 1980.

3. Джессен Р. Методы статистических обследований/ Пер. с англ. под ред. Е.М. Четыркина.—М.; Финансы и статистика, 1985.

4. Джини К. Средние величины.—М.: Статистика, 1970.

5. Кадинец Л.С. Теория индексов.—М.: Госстатиздат, 1963.

6. Кокрен У. Методы выборочного исследования / Пер. с англ. под ред. А.Г. Волкова.—М.; Статистика, 1976.

7. Методологические положения по статистике: Вып. / Госкомстат России,—М., 1996.

8. Положение "О Государственном комитете Российской Федерации по статистике", РФ № 834 от 09.07.1994 г.

9. Пасхавер И.С. Средние величины в статистике.—М.: Статистика, 1979.

10. Популярный экономико-статистический словарь-справочник/ Под ред. И.И. Елисеевой.—М.: Финансы и статистика, 1993.

11. Юзбашев М.М., Манелля А.И. Статистический анализ тенденций и колеблемости.—М.: Финансы и статистика, 1983.

12. Журнал «Вопросы статистики»

УТВЕРЖДАЮ

Проректор по учебной работе

_________________Е.В.Никифорова

«_____»___________________2005г.

Теория статистики)

Учебно-методическое пособие, методические указания

и задания к контрольной (индивидуальной) работе

для студентов экономических специальностей

Составил – к.э.н., доцент Гениатулин В.Н.

Тольятти 2005

060500 «Бухгалтерский учет, анализ и аудит»,

061100 «Менеджмент организации», 061500 «Маркетинг»,

351200 «Налоги и налогообложение»

Рассмотрены на заседании кафедры «Бухгалтерский учет, анализ и аудит»

Протокол №____от_____________2005г.

Зав. кафедрой «Бухгалтерский учет, анализ и аудит»____Е.В.Никифорова

Одобрено УМС экономического факультета

Протокол №____от_____________2005г.

Утверждено на заседании УМС ВУиТ

Протокол №____от_____________2005г.

Председатель УМС ВУиТ__________________Е.В.Никифорова

Содержание

1. Предмет статистической науки и ее методология

2. Содержание курса

3. Методические указания по выполнению контрольной работы

4. Задания к контрольной работе

5. Практикум по теории статистики

6. Вопросы к экзамену (зачету) по статистике

7. Тесты

8. Учебно-методическое обеспечение дисциплины

ПРЕДМЕТ СТАТИСТИЧЕСКОЙ НАУКИ И ЕЕ МЕТОДОЛОГИЯ

Каждая наука обладает существенными специфическими особенностями, которые отличают ее от других наук и дают ей право на самостоятельное существование как особой отрасли знания. Главная особенность любой науки заключается в предмете познания, в принципах и методах его изучения, которые в совокупности образуют ее методологию.

Предметом исследования статистики являются массовые явления социально-экономической жизни; она изучает количественную сторону этих явлений в неразрывной связи с их качественным содержанием в конкретных условиях места и времени.

Явления и процессы в жизни общества характеризуются статистикой с помощью статистических показателей. Статистические показатели – это количественная оценка свойств изучаемого явления. Статистика при помощи статистических показаний характеризует размеры изучаемых явлений, их особенности, закономерности развития и их взаимосвязи. При этом статистические показатели подразделяются на учетно-оценочные и аналитические. Учетно-оценочные показатели отражают объем или уровень изучаемого явления; аналитические показатели используются для характеристики особенностей развития явления, распространенности в пространстве, соотношения его частей, взаимосвязи с другими явлениями. В качестве аналитических показателей, используются средние величины, показатели структуры, вариации, динамики, степени тесноты связи и др.

В настоящее время основными задачами российской статистики являются:

- разработка научно обоснованной статистической методологии соответствующей потребностям общества на современном этапе, а также международным стандартам;

- представление официальной статистической информации Президенту Российской Федерации, Правительству Российской Федерации, Федеральному Собранию Российской Федерации, федеральным органам исполнительной власти, общественности, а также международным организациям;

- предоставление всем пользователям равного доступа к открытой статистической информации путем распространения официальных докладов о социально-экономическом положении Российской Федерации, субъектов Российской Федерации, отраслей и секторов экономики, публикации статистических сборников и других материалов.

Формирование информационной системы статистических показателей для всестороннего анализа экономических и социальных процессов, происходящих в стране в целом и в ее регионах, осуществляется на базе показателей, содержащихся в статистической государственной отчетности (около 700 форм) и на основе выборочных статистических обследований.

На региональном уровне проводятся дополнительные статистические наблюдения, отражающие специфику каждого региона.

Действующая в России информационная статистическая система располагает комплексом средств для обеспечения необходимой разнообразной информацией как органов государственного управления, научных учреждений, так и средств массовой информации.

В целях оперативного информирования органов государственного управления об отдельных важных тенденциях в развитие экономики систематически выпускается экспресс-информация. Снабженная кратким анализом, она поступает потребителю через несколько часов после завершения машинной обработки данных.

Правительством Российской Федерации утверждена целевая программа реформирования статистики. Целью программы является наиболее полное обеспечение потребностей федеральных органов исполнительной власти субъектов Российской Федерации и всех заинтересованных пользователей объективной и актуальной информацией о социально-экономическом развитии Российской Федерации, субъектов Российской Федерации, отраслей экономики, хозяйствующих субъектов, населения.

Опираясь на теоретическую базу, статистика применяет специфические методы цифрового освещения явления, которые находят свое выражение в трех этапах (стадиях) статистического исследования:

1. Массовое научно организованное наблюдение, с помощью которого получают первичную информацию об отдельных единицах (фактах) изучаемого явления.

2. Группировка и сводка материала, представляющие собой расчленение всей массы случаев (единиц) на однородные группы и подгруппы, подсчет итогов по каждой группе и оформление полученных результатов в виде статистической таблицы. Группировки дают возможность выделить из состава всех случаев единицы разного качества, показать особенности явлений, развивающихся в различных условиях. После проведения группировки приступают к обобщению данных наблюдения. Эта ступень носит название сводки.

3. Обработка статистических показателей, полученных при сводке и анализ результатов для получения обоснованных выводов о состоянии изучаемого явления и закономерности его развития. Выводы, как правило, излагаются в текстовой форме и сопровождаются графиками и таблицами.

Таким образом, специфический метод статистики основан на соединении анализа и синтеза. Сначала выделяются в составе изучаемого явления и раздельно изучаются части (группы и подгруппы), оценивается существенность или несущественность наблюдаемых различий в величине признака выявляются причины в целом, во всей совокупности его сторон, тенденций и форм развития. Все стадии статистической работы тесно связаны друг с другом.

Структура статистической науки предоставлена на рис.1.

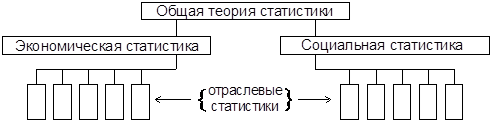Рис.1. Структура статистической науки.

Таким образом, в статистической науке выделяются следующие части: общая теория статистики, экономическая статистика и ее отрасли, социальная статистика и ее отрасли.

Общая теория статистики разрабатывает общие принципы и методы статистического исследования общественных явлений, наиболее общие категории (показатели) статистики.

Задачей экономической статистики является разработка и анализ синтетических показателей, отражающих состояние национальной экономики, взаимосвязи отраслей, особенности размещения производственных сил, наличие материальных, трудовых и финансовых ресурсов, достигнутый уровень их использования.

Статистики крупных отраслей могут быть подразделены на более мелкие отраслевые статистики: например, статистика промышленности – на статистику машиностроения, металлургии, химии и др.; статистика сельского хозяйства – на статистику земледелия и животноводства и т.п.

Социальная статистика формирует систему показателей для характеристики образа жизни населения и различных аспектов социальных отношений; ее отрасли – статистика народонаселения, политики, культуры, здравоохранения, науки, просвещения, права и т.д.

Отрасли экономической статистики – статистика промышленности, сельского хозяйства, строительства, транспорта, связи, труда, природных ресурсов, охраны окружающей среды и т.д.; их задача – разработка и анализ статистических показателей развития соответствующих отраслей. Отраслевые статистики формируются на базе показателей экономической или социальной статистики, а те другие основываются в свою очередь на категориях (показателях) и методах анализа, разработанных общей теорией статистики.

Общая теория статистики является той учебной дисциплиной с изучения которой начинается формирование необходимых знаний у экономистов, менеджеров, руководителей предприятия.

СОДЕРЖАНИЕ КУРСА

Дата: 2019-05-28, просмотров: 362.

12 3 4 5 6 7 8 9 10 Следующая ⇒