Суть приобретаемого знания в условиях неопределенности состоит в пони­мании, влияет ли полученная информация на наши ожидания относительно других событий. Основная причина трудностей при использовании систем, основанных на правилах, состоит в учете «сторонних», «косвенных» по­следствий наблюдаемых событий. Проиллюстрируем это на уже успевшем стать классическим примере.

Шерлок Холмс вышел из дома утром и заметил, что трава вокруг влаж­ная. Он рассудил: «Я думаю, что ночью был дождь. Следовательно, тра­ва возле дома моего соседа, доктора Ватсона, вероятно, также влажная». Таким образом, информация о состоянии травы у дома Холмса повлия­ла на его ожидания относительно влажности травы у дома Ватсона. Но предположим, что Холмс проверил состояние сборника дождевой воды и обнаружил, что тот - сухой. В результате Холмс вынужден изменить ход своих рассуждений, и состояние травы возле его дома перестает влиять на ожидания по поводу травы у соседа.

Теперь рассмотрим две возможные причины, почему трава у дома Холмса оказалась влажной. Помимо дождя, Холмс мог просто забыть вы­ключить поливальную установку накануне. Допустим, на следующее утро Холмс снова обнаруживает, что трава влажная. Это повышает его субъек­тивные вероятности и для прошедшего дождя, и по поводу забытой дожде­вальной установки. Затем Холмс обнаруживает, что трава у дома Ватсона также влажная и заключает, что ночью был дождь.

Следующий шаг рассуждений практически невозможно воспроизвести в системах, основанных на правилах, однако он абсолютно естественен для человека: влажность травы у дома Ватсона объясняется дождем, и следовательно нет оснований продолжать ожидать, что была забыта включенной поливальная машина. Следовательно, возросшая, было, субъективная вероятность относительно забытой поливальной машины умень­шается до (практически) исходного значения, имевшего место до выхода Холмса из дома. Такой способ рассуждения можно назвать «попутное объ­яснение», «контекстное объяснение» или «редукция причины» (explaining away).

Важная особенность «попутного объяснения» состоит в изменении от­ношений зависимости между событиями по мере поступления информа­ции. До выхода из дома Холмса факты дождя и работы поливальной уста­новки были независимы. После получения информации о траве у дома они стали зависимыми. Далее, когда появилась информации о влажности травы у дома Ватсона, состояние зависимости вновь изменилось.

Эту ситуацию удобно описать при помощи графа, узлы которого пред­ставляют события (или переменные), а пара узлов (A, B) связывается на­правленным ребром, если информация об A может служить причиной для B. В этом случае узел A будет родителем для B, который, в свою очередь, называется узлом-потомком по отношению к A.

История с травой у Холмса и Ватсона представлена на рис. 1.

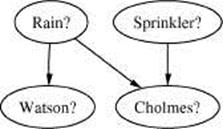
Рисунок 1 Граф рассуждений Шерлока Холмса

Граф на рис. 1 может быть отнесен к семейству байесовых сетей. В дан­ном примере переменные в узлах могут принимать только булевы значения 1 или 0 (да/нет). Из графа на рис. 1 можно сделать несколько полезных выводов о зависимости и независимости переменных. В традиционной постановке байесовы сети не предназначены для оперирования с непрерывным набором состояний (например, с действительным числом на заданном отрез­ке). Для представления действительных чисел в некоторых приложениях можно провести разбиение отрезка на сегменты и рассматривать дискретный набор их центров.

Например, если известно, что ночью не было дождя, то информация о состоянии травы у дома Ватсона не оказывает влияния на ожидания по поводу состояния травы у дома Холмса.

В середине 80-х годов были подробно проанализированы способы, ко­торыми влияние информации распространяется между переменными в байесовой сети. Будем считать, что две переменные разделены, если но­вые сведения о значении одной из них не оказывают влияния на ожидания по поводу другой. Если состояние переменной известно, мы будем назы­вать такую переменную конкретизированной.

В байесовой сети возможны три типа отношений между переменными:

1. последовательные соединения (рис. 2a);

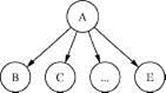
2. дивергентные соединения (рис. 2b),;

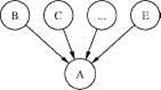
3. конвергентные соединения (рис. 2c).

Ситуация на рис. 2c требует, по-видимому, дополнительных поясне­ний—как возникает зависимость между предками конвергентного узла, когда становится известным значение потомка. Для простоты рассмот­рим пример, когда узел A имеет всего двух предков –B и C. Пусть эти две переменные отвечают за выпадение орла и решки при независимом броса­нии двух разных монет, а переменная A — логический индикатор, который «загорается», когда обе монеты оказались в одинаковом состоянии (напри­мер, обе - решки). Теперь легко понять, что если значение индикаторной переменной стало известным, то значения B и C стали зависимыми — знание одного из них полностью определяет оставшееся.

Общее свойство (условной) независимости переменных — узлов в бай­есовой сети получило название d-разделения (d-separation).

Определение d-разделимости

Две переменные A и B в байесовой сети являются d-разделенными, если на каждом пути, соединяющем эти две вершины на графе, найдется промежуточная переменная V, такая что:

1. соединение с V последовательное или дивергентное и значение V известно, либо

2. соединение конвергентное и нет свидетельств ни о значении V, ни о каждом из ее потомков.

Так, в сети задачи Шерлока Холмса (рис. 1) переменные «Полив?» и «Трава у дома Ватсона?» являются d-разделенными. Граф содержит на пути между этими переменными конвергентное соединение с переменной «Трава у до­ма Холмса?».

(a)

(b)

(c)

Рисунок 2 Три типа отношений между переменными

(a) Последовательное соединение. Влияние информации может распростра­няться от A к C и обратно, пока значение B не конкретизировано. (b) Дивер­гентное соединение. Влияние может распространяться между потомками узла A, пока его значение не конкретизировано. (c) Конвергентное соединение. Если об A ничего не известно, кроме того, что может быть выведено из информации о его предках B,C,... ,E, то эти переменные предки являются разделенными. При уточнении A открывается канал взаимного влияния между его предками.

Свойство d-разделимости соответствует особенностям логики экспер­та-человека, поэтому крайне желательно, чтобы в рассуждениях машин относительно двух d-разделенных переменных новая информация об од­ной из них не изменяла степень детерминированности второй переменной. Формально, для переменных A и C, независимых при условии B, имеет место соотношение P(A | B) = P(A | B, C).

Отметим, что интуитивное восприятие условной зависимости и неза­висимости иногда, даже в простых случаях, оказывается затрудненным, так как сложно из всех исходов событий мысленно выделить только те события, в которых значение обусловливающей переменной определено, и далее в рассуждения оперировать только ими.

Вот простой пример, поясняющий эту трудность: в некотором сообще­стве мужчины среднего возраста и молодые женщины оказались матери­ально более обеспеченными, чем остальные люди. Тогда при условии фик­сированного повышенного уровня обеспеченности пол и возраст человека оказываются условно зависимыми друг от друга!

Еще один классический пример, связанный с особенностями условных вероятностей. Рассмотрим некоторый колледж, охотно принимающий на обучение сообразительных и спортивных молодых людей (и тех, кто обла­дает обоими замечательными качествами!). Разумно считать, что среди всех молодых людей студенческого возраста спортивные и интеллектуальные показатели независимы. Теперь если вернуться к множеству зачисленных в колледж, то легко видеть, что высокая сообразительность эффективно понижает вероятность спортивности и наоборот, так как каждого из этих свойств по-отдельности достаточно для приема в колледж. Таким образом, спортивность и умственные показатели оказались зависимыми при условии обучения в колледже.