Содержание.
Содержание. 2
Введение. 3
Основные понятия и определения. 5
Законы теории вероятностей. 5
Законы сложения вероятностей. 6
Условные вероятности. 6
Формула Байеса. 7
Введение в байесовские сети доверия. 7
Моделирование в условиях неопределенности. 8
Экспертные системы и формальная логика. 8
Особенности вывода суждений в условиях неопределенности. 9
Определение d-разделимости. 11
Использование Байесовых сетей. 13
Вероятности прогнозируемых значений отдельных переменных. 13
Пример построения простейшей байесовской сети доверия. 13
Расчет в байесовской сети. 15
Байесовские сети доверия как одно из направлений современных экспертных систем. 16
Представление знаний с использованием байесовской сети доверия и условная независимость событий. 16
Замечание о субъективных вероятностях и ожидания. 17
Синтез сети на основе априорной информации. 18
Пример использования Байесовых сетей. 19
Медицина. 19
Космические и военные применения. 19
Компьютеры и системное программное обеспечение. 19
Обработка изображений и видео. 19
Финансы и экономика. 20
Описание прикладных программ.. 21
AUAI — Ассоциация анализа неопределенности в искусственном интеллекте. 21
NETICA.. 21
Knowledge Industries. 22
Data Digest Corporation. 22
BayesWare, Ltd. 22
HUGIN Expert 22
Выводы.. 24
Список используемой литературы. 25
Введение
Байесовы сети представляют собой графовые модели вероятностных и причинно-следственных отношений между переменными в статистическом информационном моделировании. В байесовых сетях могут органически сочетаться эмпирические частоты появления различных значений переменных, субъективные оценки «ожиданий» и теоретические представления о математических вероятностях тех или иных следствий из априорной информации. Это является важным практическим преимуществом и отличает байесовы сети от других методик информационного моделирования.
Наблюдаемые события редко могут быть описаны как прямые следствия строго детерминированных причин. На практике широко применяется вероятностное описание явлений. Обоснований тому несколько: и наличие неустранимых погрешностей в процессе экспериментирования и наблюдений, и невозможность полного описания структурных сложностей изучаемой системы, и неопределенности вследствие конечности объема наблюдений.
На пути вероятностного моделирования встречаются определенные сложности, которые (если отвлечься от чисто теоретических проблем) можно условно разделить на две группы:
• технические (вычислительная сложность, «комбинаторные взрывы» и т.п.);
• идейные (наличие неопределенности, сложности при постановке задачи в терминах вероятностей, недостаточность статистического материала).
Для иллюстрации одной из «идейных» сложностей рассмотрим простой пример из области вероятностного прогнозирования. Требуется оценить вероятность положительного исхода в каждой из трех ситуаций:
• Знатная леди утверждает, что она может отличить на вкус, был ли чай налит в сливки или наоборот — сливки в чай. Ей удалось это проделать 10 раз в течение бала.
• Азартный игрок утверждает, что он может предсказать, орлом или решкой выпадет монета (которую вы ему дадите). Он смог выиграть такое пари уже 10 раз за этот вечер, ни разу не проиграв!
• Эксперт в классической музыке заявляет, что он в состоянии различить творения Гайдна и Моцарта лишь по одной странице партитуры. Он уверенно проделал это 10 раз в музыкальной библиотеке.
Удивительная особенность — во всех трех случаях мы формально имеем одинаковые экспериментальные свидетельства в пользу высказанных утверждений — в каждом случае они достоверно подтверждены 10 раз. Однако мы с восхищением и удивлением отнесемся к способностям леди, весьма скептически воспримем заявления бравого игрока, и совершенно естественно согласимся с доводами музыкального эксперта. Наши субъективные оценки вероятности этих трех ситуаций весьма отличаются. И, несмотря на то, что мы имеем дело с повторяющимися событиями, весьма непросто совместить их с классическими положениями теории вероятностей.
Особенно затруднительно получить формулировку, понятную вычислительной машине.
Другая сторона идейных трудностей возникает при практической необходимости вероятностного прогнозирования событий, к которым не вполне применимы классические представления о статистической повторяемости. Представим себе серию экспериментов с бросанием кубика, сделанного из сахара, на влажную поверхность стола. Вероятности исходов последующих испытаний зависят от относительной частоты исходов предыдущих испытаний, при этом исследуемая система каждый раз необратимо изменяется в результате каждого эксперимента. Этим свойством обладают многие биологические и социальные системы, что делает их вероятностное моделирование классическими методами крайне проблематичным.
Часть из указанных проблем решается в вероятностных байесовых сетях, которые представляют собой графовые модели причинно-следственных отношений между случайными переменными. В байесовых сетях могут органически сочетаться эмпирические частоты появления различных значений переменных, субъективные оценки «ожиданий» и теоретические представления о математических вероятностях тех или иных следствий из априорной информации. Это является важным практическим преимуществом и отличает байесовы сети от других методик информационного моделирования.
Байесовы сети широко применяются в таких областях, как медицина, стратегическое планирование, финансы и экономика.
Основные понятия и определения
Законы теории вероятностей.
Понятие вероятности ассоциируется с проведением эксперимента, результаты которого, именуемые исходами, изменяются случайным образом. Множество всех возможных исходов эксперимента называется пространством элементарных событий, а любое подмножество этого пространства – событием.
Эксперимент может быть связан также с непрерывным пространством событий.
Если в эксперименте, состоящем из n опытов, событие Е имело место m раз, то вероятность P{E} появления события Е математически определяется соотношением
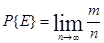
Приведенное определение означает, что если эксперимент повторяется бесконечное число раз, то, искомая вероятность представляется граничным значение дроби m/n.
По определению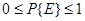 
, где вероятность P{E} равна 0, если событие E невозможно, и 1, если оно достоверно.
Условные вероятности.
Для двух события E и F условная вероятность события E при условии, что наступило событие F, обозначается как P{E|F} и определяется по формуле
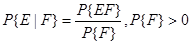
Если событие E содержится в событии F (т.е. множество исходов E является подмножеством исходов F), тогда
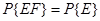
Два события E и F являются независимыми тогда и только тогда, когда выполняется равенство P{E|F}=P{E}. В этом случае формула условной вероятности сводится к следующему
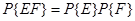
Теорема умножения, если соответствующие условные вероятности определены
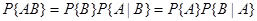
Теорема умножения для большого числа событий, если соответствующие условные вероятности определены
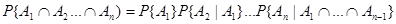
Формула полной вероятности для группы несовместных событий Bi
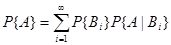
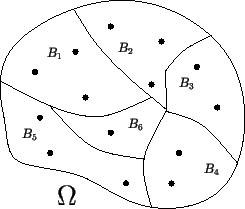
Формула Байеса.
Пусть Ai – полная группа несовместных событий, тогда формула Байеса (формула перерасчета гипотез) и B некоторое событие положительной вероятности
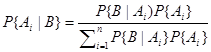
Доказательство следует из теоремы умножения и формулы полной вероятности.
Определение d-разделимости
Две переменные A и B в байесовой сети являются d-разделенными, если на каждом пути, соединяющем эти две вершины на графе, найдется промежуточная переменная V, такая что:
1. соединение с V последовательное или дивергентное и значение V известно, либо
2. соединение конвергентное и нет свидетельств ни о значении V, ни о каждом из ее потомков.
Так, в сети задачи Шерлока Холмса (рис. 1) переменные «Полив?» и «Трава у дома Ватсона?» являются d-разделенными. Граф содержит на пути между этими переменными конвергентное соединение с переменной «Трава у дома Холмса?».
(a)
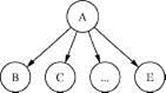
(b)
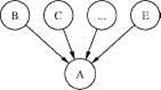
(c)
Рисунок 2 Три типа отношений между переменными
(a) Последовательное соединение. Влияние информации может распространяться от A к C и обратно, пока значение B не конкретизировано. (b) Дивергентное соединение. Влияние может распространяться между потомками узла A, пока его значение не конкретизировано. (c) Конвергентное соединение. Если об A ничего не известно, кроме того, что может быть выведено из информации о его предках B,C,... ,E, то эти переменные предки являются разделенными. При уточнении A открывается канал взаимного влияния между его предками.
Свойство d-разделимости соответствует особенностям логики эксперта-человека, поэтому крайне желательно, чтобы в рассуждениях машин относительно двух d-разделенных переменных новая информация об одной из них не изменяла степень детерминированности второй переменной. Формально, для переменных A и C, независимых при условии B, имеет место соотношение P(A | B) = P(A | B, C).
Отметим, что интуитивное восприятие условной зависимости и независимости иногда, даже в простых случаях, оказывается затрудненным, так как сложно из всех исходов событий мысленно выделить только те события, в которых значение обусловливающей переменной определено, и далее в рассуждения оперировать только ими.
Вот простой пример, поясняющий эту трудность: в некотором сообществе мужчины среднего возраста и молодые женщины оказались материально более обеспеченными, чем остальные люди. Тогда при условии фиксированного повышенного уровня обеспеченности пол и возраст человека оказываются условно зависимыми друг от друга!
Еще один классический пример, связанный с особенностями условных вероятностей. Рассмотрим некоторый колледж, охотно принимающий на обучение сообразительных и спортивных молодых людей (и тех, кто обладает обоими замечательными качествами!). Разумно считать, что среди всех молодых людей студенческого возраста спортивные и интеллектуальные показатели независимы. Теперь если вернуться к множеству зачисленных в колледж, то легко видеть, что высокая сообразительность эффективно понижает вероятность спортивности и наоборот, так как каждого из этих свойств по-отдельности достаточно для приема в колледж. Таким образом, спортивность и умственные показатели оказались зависимыми при условии обучения в колледже.
Пример построения простейшей байесовской сети доверия.
Рассматриваем небольшую яблочную плантацию «яблочного Джека». Однажды Джек обнаружил, что его прекрасное яблочное дерево лишилось листвы. Теперь он хочет выяснить, почему это случилось. Он знает, что листва часто опадает, если:
дерево засыхает в результате недостатка влаги; или дерево болеет.
Данная ситуация может быть смоделирована байесовской сетью доверия, содержащей 3 вершины: «Болеет», «Засохло» и «Облетело».
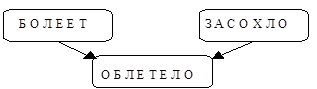
Рис.1. Пример байесовской сети доверия с тремя событиями.
В данном простейшем случае рассмотрим ситуацию, при которой каждая вершина может принимать всего лишь два возможных состояний и, как следствие находится в одном из них, а именно:
| Вершина (событие) БСД | Состояние 1 | Состояние 2 |
| “Болеет” | «болеет» | «нет» |
| “Засохло” | «засохло» | «нет» |
| “Облетело” | «да» | «нет» |
Вершина “Болеет” говорит о том, что дерево заболело, будучи в состоянии «болеет», в противном случае она находится в состоянии «нет». Аналогично для других двух вершин. Рассматриваемая байесовская сеть доверия, моделирует тот факт, что имеется причинно-следственная зависимость от события “Болеет” к событию “Облетело” и от события “Засохло” к событию “Облетело”. Это отображено стрелками на байесовской сети доверия.
Когда есть причинно-следственная зависимость от вершины А к другой вершине B, то мы ожидаем, что когда A находится в некотором определённом состоянии, это оказывает влияние на состояние B. Следует быть внимательным, когда моделируется зависимость в байесовских сетях доверия. Иногда совсем не очевидно, какое направление должна иметь стрелка.
Например, в рассматриваемом примере, мы говорим, что имеется зависимость от “Болеет” к “Облетело”, так как когда дерево болеет, это может вызывать опадание его листвы. Опадание листвы является следствием болезни, а не болезнь – следствием опадания листвы.
На приведенном выше рисунке дано графическое представление байесовской сети доверия. Однако, это только качественное представление байесовской сети доверия. Перед тем, как назвать это полностью байесовской сетью доверия необходимо определить количественное представление, то есть множество таблиц условных вероятностей:
| Априорная вероятность p(“Болеет”) | Априорная вероятность p(“Засохло”) | |||
| Болеет = «болеет» | Болеет = «нет» | Засохло = «засохло» | Засохло = «нет» | |
| 0,1 | 0,9 | 0,1 | 0,9 | |
| Таблица условных вероятностей p(“Облетело” | ”Болеет”, ”Засохло”) | ||||
| Засохло = «засохло» | Засохло = «нет» | |||
| Болеет = «болеет» | Болеет = «нет» | Болеет = «болеет» | Болеет = «нет» | |
| Облетело = «да» | 0,95 | 0,85 | 0,90 | 0,02 |
| Облетело = «нет» | 0,05 | 0,15 | 0,10 | 0,98 |
Приведенные таблицы иллюстрируют ТУВ для трёх вершин байесовской сети доверия. Заметим, что все три таблицы показывают вероятность пребывания некоторой вершины в определённом состоянии, обусловленным состоянием её родительских вершин. Но так как вершины Болеет и Засохло не имеют родительских вершин, то их вероятности являются маргинальными, т.е. не зависят (не обусловлены) ни от чего.
На данном примере мы рассмотрели, что и как описывается очень простой байесовской сетью доверия. Современные программные средства (такие как MSBN, Hugin и др.) обеспечивают инструментарий для построения таких сетей, а также возможность использования байесовских сетей доверия для введения новых свидетельств и получения решения (вывода) за счёт пересчёта новых вероятностей во всех вершинах, соответствующих вновь введенным свидетельствам.
В нашем примере пусть известно, что дерево сбросило листву. Это свидетельство вводится выбором состояния «да» в вершине “Облетело”. После этого можно узнать вероятности того, что дерево засохло. Для приведенных выше исходных данных, результаты вывода путем распространения вероятностей по БСД будут:
p( “Болеет” = «болеет» | “Облетело” = «да») = 0,47; p( “Засохло” = «засохло» | “Облетело” = «да») = 0,49.
Расчет в байесовской сети.
Следует отметить, что следствием байесовской теоремы является то, что она поддерживает оценку графа в обоих направлениях. Процесс рассуждения в ЭС сопровождается распространением по сети вновь поступивших свидетельств.
Введение в байесовские сети доверия новых данных приводит к возникновению переходного процесса распространения по байесовской сети доверия вновь поступившего свидетельства. После завершения переходного процесса каждому высказыванию, ассоциированному с вершинами графа, приписывается апостериорная вероятность, которая определяет степень доверия к этому высказыванию ( believe – доверять(англ.) ):
,
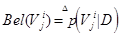где D – объединения всех поступивших в систему данных;
Vji – композиционные высказывания, составленные из элементарных, то есть множество значений Xi составляют Vji ;
Xi – пропозиционные переменные (то есть переменные, значениями которых являются высказывания), определяющие состояние вершин БСД.
При этом процесс распространения вероятностей в БСД основывается на механизме пересчёта, в основе функционирования которого лежит следующая последовательность действий:
С каждой вершиной сети ассоциирован вычислительный процесс (процессор), который получает сообщения от соседних (связанных с ним дугами) процессоров.
Этот процессор осуществляет пересчёт апостериорных вероятностей Bel(Vji) для всех возможных значений Vji данной переменной Xi и посылает соседим вершинам ответные сообщения.
Деятельность процессора инициируется нарушением условий согласованности с состояниями соседних процессоров и продолжается до восстановления этих условий.
В некоторых системах, реализующих байесовские сети доверия используется метод noisy or gate, позволяющий существенно упростить вычислительный процесс. Суть его заключается в том, что в ряде примеров вершина «y» может быть условно независима от целого ряда вершин «xr» , где r = 1,2,..., n. Для того, чтобы сократить оценку 2n вероятностей, которые необходимы при использовании таблиц условных вероятностей, и используется данный метод. Согласно ему вероятность «y» в зависимости от n вершин «xr» оценивается как
,
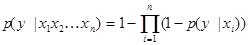что позволяет оценить только p(y | x 1), p(y | x 2) ... p(y | x n), и на их основании определить оценку p( y | x1 x2 ... xn).
Пример использования Байесовых сетей
Естественной областью использования байесовых сетей являются экспертные системы, которые нуждаются в средствах оперирования с вероятностями.
Медицина
Система PathFinder (Heckerman, 1990) разработана для диагностики заболеваний лимфатических узлов. PathFinder включает 60 различных вариантов диагноза и 130 переменных, значения которых могут наблюдаться при изучении клинических случаев. Система смогла приблизиться к уровню экспертов, и ее версия PathFinder-4 получила коммерческое распространение.
Множество других разработок (Child, MUNIN, Painulim, SWAN и др.) успешно применяются в различных медицинских приложениях .
Финансы и экономика
В серии работ школы бизнеса Университета штата Канзас описаны байесовы методики оценки риска и прогноза доходности портфелей финансовых инструментов. Основными достоинствами байесовых сетей в финансовых задачах является возможность совместного учета количественных и качественных рыночных показателей, динамическое поступление новой информации, а также явные зависимости между существенными факторами, влияющими на финансовые показатели.
Результаты моделирования представляются в форме гистограмм распределений вероятностей, что позволяет провести детальный анализ соотношений «риск-доходность». Весьма эффективными являются также широкие возможности по игровому моделированию.
NETICA
(URL: http://www.norsys.com/index.html)
Norsys Software Corp. — частная компания, Расположенная в Ванкувере (Канада). Norsys специализируется в разработке программного обеспечения для байесовых сетей. Программа Netica —основное достижение компании, разрабатывается с 1992 года и стала коммерчески доступной в 1995 году. В настоящее время Netica является одним из наиболее широко используемых инструментов для разработки байесовых сетей.
Версия программы с ограниченной функциональностью свободно доступна на сайте фирмы Norsys.
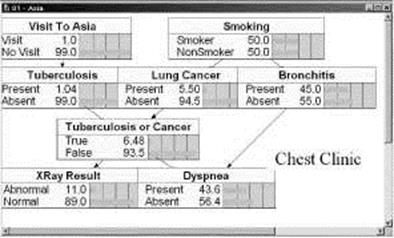
Рисунок 1 Пример байесовой сети в приложении Netica
Netica — мощная, удобная в работе программа для работы с графовыми вероятностными моделями. Она имеет интуитивный и приятный интерфейс пользователя для ввода топологии сети. Соотношения между переменными могут быть заданы, как индивидуальные вероятности, в форме уравнений, или путем автоматического обучения из файлов данных (которые могут содержать пропуски).
Созданные сети могут быть использованы независимо, и как фрагменты более крупных моделей, формируя тем самым библиотеку модулей. При создании сетевых моделей доступен широкий спектр функций и инструментов.
Многие операции могут быть сделаны несколькими щелчками мыши, что делает систему Netica весьма удобной для поисковых исследований, и для обучения и для простого просмотра, и для обучения модели байесовой сети. Система Netica постоянно развивается и совершенствуется.
Knowledge Industries
(URL: http://www.kic.com/)
Knowledge Industries —ведущий поставщик программных инструментальных средств для разработки и внедрения комплексных диагностических систем. При проектировании сложных и дорогостоящих вариантов систем диагностик в компании используется байесовы сети собственной разработки.
Data Digest Corporation
(URL: http://www.data-digest.com/home.html)
Data Digest Corporation является одним из лидеров в применении методов байесовых сетей к анализу данных.
BayesWare, Ltd
(URL: http://www.bayesware.com/corporate/profile.html)
Компания BayesWare основана в 1999 году. Она производит и поддерживает программное обеспечение, поставляет изготовленные на заказ решения, предоставляет программы обучения, и предлагает услуги консультирования корпоративным заказчикам и общественным учреждениям. Одна из успешных разработок компании, Bayesware Discoverer, основана на моделях байесовых сетей.
HUGIN Expert
(URL: http://www.hugin.com/)
Компания Hugin Expert была основана в 1989 году в Ольборге, (Дания). Их основной продукт Hugin начал создаваться во время работ по проекту ESPRIT, в котором системы, основанные на знаниях, использовались для проблемы диагностирования нервно-мышечных заболеваний. Затем началась коммерциализация результатов проекта и основного инструмента — программы Hugin. К настоящему моменту Hugin адаптирована во многих исследовательских центрах компании в 25 различных странах, она используется в ряде различных областей, связанных с анализом решений, поддержкой принятия решений, предсказанием, диагностикой, управлением рисками и оценками безопасности технологий.
Hugin является программой реализацией системы принятия решений на основе байесовских сетей доверия. Имеет две версии Pro и Explorer. Функционирует в среде OS Windows’95, Windows NT, а также имеет версию UNIX. Эта система имеет развитый интерфейс и позволяет достаточно просто создавать базы знаний и фактов. Использует два основных режима работы:
режим редактирования и построения причинно-следственной сети, а также заполнения таблиц условных вероятностей, являющихся количественным описанием БЗ.
режим расчёта вероятностных оценок для принятия решения по всем событиям, входящим в причинно-следственную сеть. Расчёты могут осуществляться как на основе классической теории Байеса, так и на основе методов теории возможностей.
“Hugin” имеет возможность связи с основными наиболее распространёнными программными средствами фирмы Microsoft. Данная ЭС имеет все основные функции любой информационной системы, включая такие как: хранение данных, вывод на принтер всех элементов ЭС, диагностика ошибок в работе.
Выводы
Байесовы вероятностные методы обучения машин являются существенным шагом вперед, в сравнении с популярными моделями «черных ящиков». Они дают понятное объяснение своих выводов, допускают логическую интерпретацию и модификацию структуры отношений между переменными задачи, а также позволяют в явной форме учесть априорный опыт экспертов в соответствующей предметной области.
Благодаря удачному представлению в виде графов, байесовы сети весьма удобны в пользовательских приложениях.
Байесовы сети базируются на фундаментальных положениях и результатах теории вероятностей, разрабатываемых в течение нескольких сотен лет, что и лежит в основе их успеха в практической плоскости.
Байесова методология, в действительности, шире, чем семейство способов оперирования с условными вероятностями в ориентированных графах. Она включает в себя также модели с симметричными связями (случайные поля и решетки), модели динамических процессов (марковские цепи), а также широкий класс моделей со скрытыми переменными, позволяющих решать вероятностные задачи классификации, распознавания образов и прогнозирования.
В ближайшем будущем предполагается значительно расширить применение Байесовых сетей доверия. Например, на одном из сайтов поисковиков конструируются байесовские сети для моделирования успешных запросов, поступающих от пользователей. Эти сети могут пополнять регистрационный файл поискового сервера назначаемыми категориями предполагаемых целей информации для обеспечения возможности предсказания модификаций запросов.
Список используемой литературы.
1. Таха Х.А., Введение в исследование операций, Вильямс, Киев, 2005.
2. Терехов С.А., Лекции по нейроинформатике, МИФИ, М., 2003.
3. Хабаров С., Экспертные системы, M., 2003.
4. Чернова Н.И., Математические методы и исследование операций в эк., М., 2000.
5. http://www.ai.mit.edu/˜ murphyk/Software/BNT/bnsoft.html. Описание программных продуктов для работы с байесовскими сетями.
Содержание.
Содержание. 2
Введение. 3
Основные понятия и определения. 5
Законы теории вероятностей. 5
Законы сложения вероятностей. 6
Условные вероятности. 6
Формула Байеса. 7
Введение в байесовские сети доверия. 7
Моделирование в условиях неопределенности. 8
Экспертные системы и формальная логика. 8
Особенности вывода суждений в условиях неопределенности. 9
Определение d-разделимости. 11
Использование Байесовых сетей. 13
Вероятности прогнозируемых значений отдельных переменных. 13
Пример построения простейшей байесовской сети доверия. 13
Расчет в байесовской сети. 15
Байесовские сети доверия как одно из направлений современных экспертных систем. 16
Представление знаний с использованием байесовской сети доверия и условная независимость событий. 16
Замечание о субъективных вероятностях и ожидания. 17
Синтез сети на основе априорной информации. 18
Пример использования Байесовых сетей. 19
Медицина. 19
Космические и военные применения. 19
Компьютеры и системное программное обеспечение. 19
Обработка изображений и видео. 19
Финансы и экономика. 20
Описание прикладных программ.. 21
AUAI — Ассоциация анализа неопределенности в искусственном интеллекте. 21
NETICA.. 21
Knowledge Industries. 22
Data Digest Corporation. 22
BayesWare, Ltd. 22
HUGIN Expert 22
Выводы.. 24
Список используемой литературы. 25
Введение
Байесовы сети представляют собой графовые модели вероятностных и причинно-следственных отношений между переменными в статистическом информационном моделировании. В байесовых сетях могут органически сочетаться эмпирические частоты появления различных значений переменных, субъективные оценки «ожиданий» и теоретические представления о математических вероятностях тех или иных следствий из априорной информации. Это является важным практическим преимуществом и отличает байесовы сети от других методик информационного моделирования.
Наблюдаемые события редко могут быть описаны как прямые следствия строго детерминированных причин. На практике широко применяется вероятностное описание явлений. Обоснований тому несколько: и наличие неустранимых погрешностей в процессе экспериментирования и наблюдений, и невозможность полного описания структурных сложностей изучаемой системы, и неопределенности вследствие конечности объема наблюдений.
На пути вероятностного моделирования встречаются определенные сложности, которые (если отвлечься от чисто теоретических проблем) можно условно разделить на две группы:
• технические (вычислительная сложность, «комбинаторные взрывы» и т.п.);
• идейные (наличие неопределенности, сложности при постановке задачи в терминах вероятностей, недостаточность статистического материала).
Для иллюстрации одной из «идейных» сложностей рассмотрим простой пример из области вероятностного прогнозирования. Требуется оценить вероятность положительного исхода в каждой из трех ситуаций:
• Знатная леди утверждает, что она может отличить на вкус, был ли чай налит в сливки или наоборот — сливки в чай. Ей удалось это проделать 10 раз в течение бала.
• Азартный игрок утверждает, что он может предсказать, орлом или решкой выпадет монета (которую вы ему дадите). Он смог выиграть такое пари уже 10 раз за этот вечер, ни разу не проиграв!
• Эксперт в классической музыке заявляет, что он в состоянии различить творения Гайдна и Моцарта лишь по одной странице партитуры. Он уверенно проделал это 10 раз в музыкальной библиотеке.
Удивительная особенность — во всех трех случаях мы формально имеем одинаковые экспериментальные свидетельства в пользу высказанных утверждений — в каждом случае они достоверно подтверждены 10 раз. Однако мы с восхищением и удивлением отнесемся к способностям леди, весьма скептически воспримем заявления бравого игрока, и совершенно естественно согласимся с доводами музыкального эксперта. Наши субъективные оценки вероятности этих трех ситуаций весьма отличаются. И, несмотря на то, что мы имеем дело с повторяющимися событиями, весьма непросто совместить их с классическими положениями теории вероятностей.
Особенно затруднительно получить формулировку, понятную вычислительной машине.
Другая сторона идейных трудностей возникает при практической необходимости вероятностного прогнозирования событий, к которым не вполне применимы классические представления о статистической повторяемости. Представим себе серию экспериментов с бросанием кубика, сделанного из сахара, на влажную поверхность стола. Вероятности исходов последующих испытаний зависят от относительной частоты исходов предыдущих испытаний, при этом исследуемая система каждый раз необратимо изменяется в результате каждого эксперимента. Этим свойством обладают многие биологические и социальные системы, что делает их вероятностное моделирование классическими методами крайне проблематичным.
Часть из указанных проблем решается в вероятностных байесовых сетях, которые представляют собой графовые модели причинно-следственных отношений между случайными переменными. В байесовых сетях могут органически сочетаться эмпирические частоты появления различных значений переменных, субъективные оценки «ожиданий» и теоретические представления о математических вероятностях тех или иных следствий из априорной информации. Это является важным практическим преимуществом и отличает байесовы сети от других методик информационного моделирования.
Байесовы сети широко применяются в таких областях, как медицина, стратегическое планирование, финансы и экономика.
Основные понятия и определения
Законы теории вероятностей.
Понятие вероятности ассоциируется с проведением эксперимента, результаты которого, именуемые исходами, изменяются случайным образом. Множество всех возможных исходов эксперимента называется пространством элементарных событий, а любое подмножество этого пространства – событием.
Эксперимент может быть связан также с непрерывным пространством событий.
Если в эксперименте, состоящем из n опытов, событие Е имело место m раз, то вероятность P{E} появления события Е математически определяется соотношением
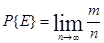
Приведенное определение означает, что если эксперимент повторяется бесконечное число раз, то, искомая вероятность представляется граничным значение дроби m/n.
По определению 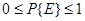, где вероятность P{E} равна 0, если событие E невозможно, и 1, если оно достоверно.
Законы сложения вероятностей.
Для двух событий E и F запись E+F означает их объединение, а EF – пересечение. События E и F называются несовместными (взаимно исключающими), если они не пересекаются, т.е. наступление одного события исключает возможность реализации другого. При принятых определениях закон сложения вероятностей определяется соотношением
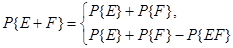
Первая строка системы в случае несовместности E и F, вторая - иначе.
Вероятность того, что события E и F произойдут одновременно, обозначается как P{EF}. Если эти события независимы, тогда
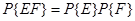
Условные вероятности.
Для двух события E и F условная вероятность события E при условии, что наступило событие F, обозначается как P{E|F} и определяется по формуле
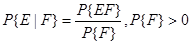
Если событие E содержится в событии F (т.е. множество исходов E является подмножеством исходов F), тогда
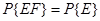
Два события E и F являются независимыми тогда и только тогда, когда выполняется равенство P{E|F}=P{E}. В этом случае формула условной вероятности сводится к следующему
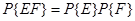
Теорема умножения, если соответствующие условные вероятности определены
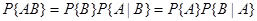
Теорема умножения для большого числа событий, если соответствующие условные вероятности определены
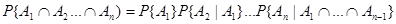
Формула полной вероятности для группы несовместных событий Bi
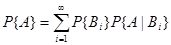
Формула Байеса.
Пусть Ai – полная группа несовместных событий, тогда формула Байеса (формула перерасчета гипотез) и B некоторое событие положительной вероятности
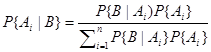
Доказательство следует из теоремы умножения и формулы полной вероятности.
Дата: 2019-05-28, просмотров: 281.
