137. Задание {{ 138 }} ТЗ № 138
Неинерциальная система отсчета – это система, которая относительно инерциальной системы отсчета
£ движется прямолинейно и равномерно
R движется с ускорением
£ покоится
138. Задание {{ 139 }} ТЗ № 139
Силы инерции обусловлены
£ взаимодействием тел в системе отсчета
R ускоренным движением системы отсчета
£ ускоренным движением тел в системе отсчета
£ равномерным прямолинейным движением системы отсчета
139. Задание {{ 140 }} ТЗ № 140
На покоящиеся тела во вращающейся системе отсчета действует
R только центробежная сила
£ только сила Кориолиса
£ и центробежная сила, и сила Кориолиса
140. Задание {{ 141 }} ТЗ № 141
На движущиеся тела во вращающейся системе отсчета действует
£ только центробежная сила
£ только сила Кориолиса
R и центробежная сила, и сила Кориолиса
141. Задание {{ 142 }} ТЗ № 142
Сила инерции при ускоренном поступательном движении системы отсчета равна
£ 
£ 
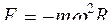
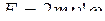
R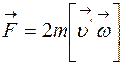 
142. Задание {{ 143 }} ТЗ № 143
Центробежная сила инерции имеет вид
£ 
£
£
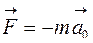
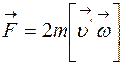
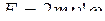
R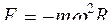
143. Задание {{ 144 }} ТЗ № 144
Кориолиса сила инерции имеет вид
R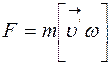 
£
£
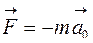
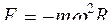
144. Задание {{ 145 }} ТЗ № 145
Основное уравнение динамики в неинерциальной системе отсчета имеет вид
£ 
£ 
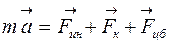
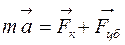
R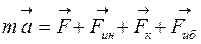 
£ 
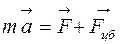
145. Задание {{ 146 }} ТЗ № 146
При увеличении массы тела в 4 раза центробежная сила инерции
R увеличивается в 4 раза
£ уменьшается в 4 раза
£ не изменяется
146. Задание {{ 147 }} ТЗ № 147
При уменьшении массы тела в 16 раз Кориолисова сила инерции
£ не изменится
R уменьшится в 16 раз
£ уменьшится в 4 раза
£ уменьшится в 2 раза
147. Задание {{ 148 }} ТЗ № 148
При уменьшении угловой скорости вращения системы отсчета в 4 раза центробежная сила инерции
£ уменьшится в 2 раза
£ уменьшится в 4 раза
R уменьшится в 16 раз
£ не изменится
148. Задание {{ 149 }} ТЗ № 149
При увеличении частоты вращения системы отсчета в 4 раза сила Кориолиса
R увеличивается в 16 раз
£ увеличивается в 4 раза
£ уменьшается в 4 раза
£ не изменяется
Механика жидкостей
149. Задание {{ 150 }} ТЗ № 150
Условие плавания тела в жидкости определяется
£ объёмом тела
£ массой тела
£ формой и массой тела
R соотношением плотностей тела и жидкости
150. Задание {{ 151 }} ТЗ № 151
Тело плавает в керосине (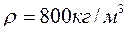 
) погружаясь на половину своего объема. Часть объёма этого же тела, погруженного в воду, будет
£ 
£ 
£ 
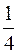
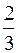
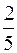
151. Задание {{ 152 }} ТЗ № 152
Два тела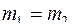 
c разной плотностью 
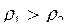погружены в одну жидкость. Выталкивающие силы будут
£ 
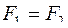
R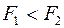 
£ 
£ 
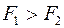
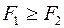
152. Задание {{ 153 }} ТЗ № 153
При уменьшении глубины погружения тела в 3 раза выталкивающая сила
£ уменьшилась в 3 раза
£ увеличилась в 3 раза
£ уменьшилась в 9 раз
R не изменилась
153. Задание {{ 154 }} ТЗ № 154
На тело объёмом 2м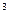 
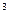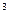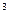и плотностью 500 кг/м , наполовину погруженное в воду плотностью 10 кг/м , действует сила Архимеда, которая равна
R 20кН
£ 5кН
£ 2кН
154. Задание {{ 155 }} ТЗ № 155
выше на 3см
£ выше на 3,5см
R ниже на 3см
£ Гидростатическое давление жидкости равно
£ 
£ 
£ 
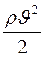
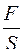
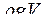
R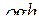 
156. Задание {{ 157 }} ТЗ № 157
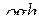
R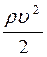 
£
£
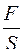
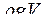
157. Задание {{ 158 }} ТЗ № 158
Глубина озера, где гидростатическое давление воды (с учётом атмосферного) 5*10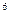 
Па, будет равна [м]
£ 500
£ 510
R 50
158. Задание {{ 159 }} ТЗ № 159
Глубина озера, где гидростатическое давление воды (без учета атмосферного) 4*10 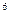Па будет равна [м]
£ 4000
R 400
£ 40
£ 4
159. Задание {{ 160 }} ТЗ № 160
Бак высотой 2 м заполнен водой. На малое отверстие в баке на высоте 0,5 м от основания действует давление (с учетом атмосферного) кПа
£ 1
£ 1,5
£ 15
R 115
160. Задание {{ 161 }} ТЗ № 161
Если к малому поршню площадью 25см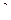 
приложена сила 200Н, то на большой поршень площадью 0,1м 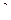действует сила
£ 2 Н
£ 5 Н
£ 500 Н
R 8000 Н
161. Задание {{ 162 }} ТЗ № 162
Жидкость, плотность которой не зависит от давления, является
£ реальной
£ идеальной
£ стационарно текущей
R несжимаемой
162. Задание {{ 163 }} ТЗ № 163
Жидкость, скорость которой в каждой её точке не изменяется, является
£ идеальной
R стационарно текущей
£ несжимаемой
163. Задание {{ 164 }} ТЗ № 164
Жидкость, внутренним трением в которой можно пренебречь, является
£ несжимаемой
R идеальной
£ стационарно текущей
£ реальной
164. Задание {{ 165 }} ТЗ № 165
Вязкость- это свойство жидкости
£ стационарно текущей
R реальной
£ несжимаемой
165. Задание {{ 166 }} ТЗ № 166
Уравнение неразрывности для несжимаемой жидкости имеет вид
£ 
£ 
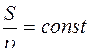
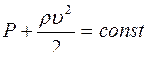
R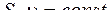 
£ 
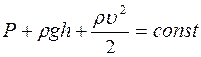
166. Задание {{ 167 }} ТЗ № 167
Уравнение Бернулли для стационарно текущей идеальной жидкости имеет вид
R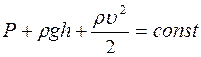 
£ 
£ 
£ 
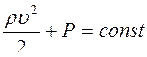
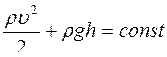
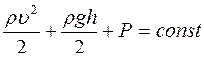
167. Задание {{ 168 }} ТЗ № 168
Уравнение Бернулли в горизонтальной трубке тока имеет вид
R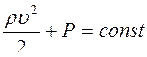
£ 
£ 
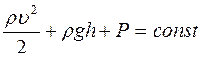
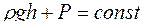
168. Задание {{ 169 }} ТЗ № 169
Скорость истечения жидкости через малое отверстие в стенке равно
£ 
£ 
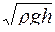
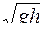
R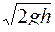 
£ 
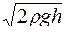
169. Задание {{ 170 }} ТЗ № 170
При переходе воды из одной трубы в другую, диаметр которой в 2 раза меньше, скорость течения
£ уменьшается в 2 раза
£ уменьшается в 4 раза
£ увеличивается в 2 раза
R увеличивается в 4 раза
170. Задание {{ 171 }} ТЗ № 171
При переходе воды из квадратной трубы со стороной в 1м в круглую с радиусом 1м скорость течения
£ не изменилась
£ увеличилась в 3,14 раз
R уменьшилась в 3,14 раз
£ увеличилась в 2 раза
171. Задание {{ 172 }} ТЗ № 172
Скорость течения воды увеличилась в 9 раз при переходе из одной трубы в другую, диаметр которой
£ увеличился в 9 раз
£ уменьшился в 9 раз
£ увеличился в 3 раза
R уменьшился в 3 раза
172. Задание {{ 173 }} ТЗ № 173
Скорость течения воды в широкой части трубы 20см/с. При уменьшении диаметра трубы в 1,5 раза скорость воды будет равна (см/с)
£ 30
£ 1,33
£ 60
R 45
173. Задание {{ 174 }} ТЗ № 174
Разность уровней 
жидкостей в одинаковых манометрических трубках 10см. Скорость течения жидкостей по горизонтальной трубе равна [м/с]
£ 1
£ 2
£ 3
R 1,4
174. Задание {{ 175 }} ТЗ № 175
По горизонтальной трубе течет жидкость со скоростью 1 м/с. Разность уровней жидкости в манометрических трубках одинакового диаметра [cм]
£ 2
R 5
£ 10
£ 12
175. Задание {{ 176 }} ТЗ № 176
Высота уровня жидкости над отверстием в стенке сосуда 1,8 м. Скорость истечения жидкости из малого отверстия равна [м/с]
£ 4,2
R 6
£ 3
£ 2,5
176. Задание {{ 177 }} ТЗ № 177
Закон Ньютона для вязкости имеет вид
£ 
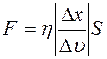
R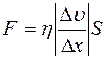 
£ 
£ 
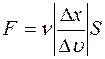
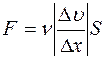
177. Задание {{ 178 }} ТЗ № 178
Вязкость в метоле Стокса определяется по формуле
£ 
£ 
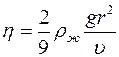
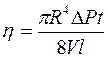
R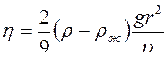 
£ 
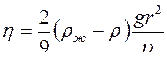
178. Задание {{ 179 }} ТЗ № 179
Вязкость в методе Пуазеля определяется по формуле
£
£
£
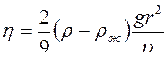
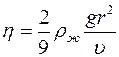
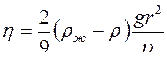
R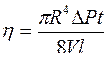 
179. Задание {{ 180 }} ТЗ № 180
Характер течения жидкости определяется безразмерной величиной
R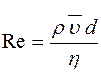 
£ 
£ 
£ 
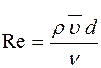
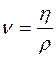
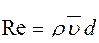
180. Задание {{ 181 }} ТЗ № 181
Число Рейнольдса зависит от
£ массы
£ давления
R вязкости
£ объема
181. Задание {{ 182 }} ТЗ № 182
Ламинарное течение наблюдается при значениях числа Рейнольдса
£ 
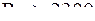
R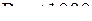 
£ 
£ 
182. Задание {{ 183 }} ТЗ № 183
Переход от ламинарного течения к турбулентному наблюдается при значениях числа Рейнольдса
£
£
£
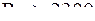
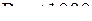
R
183. Задание {{ 184 }} ТЗ № 184
Турбулентное течение наблюдается при значениях числа Рейнольдса
£
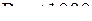
R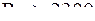
£
£
Дата: 2019-04-23, просмотров: 232.
