СОДЕРЖАНИЕ И СТРУКТУРА ТЕСТОВЫХ МАТЕРИАЛОВ
Тематическая структура
Тема
Элементы кинематики
Динамика материальной точки и поступательного движения твердых тел
Энергия. Работа. Мощность. Законы сохранения в механике
Механика твердого тела
Неинерциальные системы отсчета
Механика жидкостей
Механические колебания и волны
Специальная теория относительности
Молекулярно-кинетическая теория идеальных газов
Основы термодинамики
Реальные газы, жидкости и твердые тела
СОДЕРЖАНИЕ ТЕСТОВЫХ МАТЕРИАЛОВ
Элементы кинематики
1. Задание {{ 1 }} ТЗ № 1
Путь при равномерном прямолинейном движении определяется по формуле
R 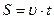
£ 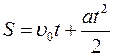
£ 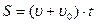
£ 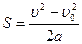
2. Задание {{ 2 }} ТЗ № 2
Путь при равноускоренном прямолинейном движении определяется по формуле
£ 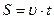
R 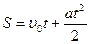
£ 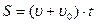
£ 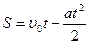
3. Задание {{ 3 }} ТЗ № 3
Путь при равнозамедленном прямолинейном движении определяется по формуле
£ 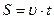
£ 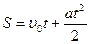
£ 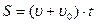
R 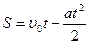
4. Задание {{ 4 }} ТЗ № 4
Мгновенное значение скорости определяется формулой
R 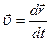
£ 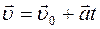
£ 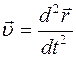
£ 
5. Задание {{ 5 }} ТЗ № 5
Мгновенное значение ускорения определяется формулой
£ 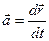
R 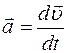
£ 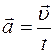
£ 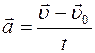
6. Задание {{ 6 }} ТЗ № 6
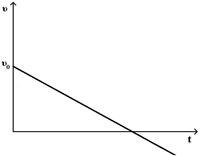
При равномерном движении материальной точки зависимость скорости от времени имеет вид
R 
£ 
£ 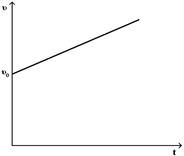
£ 
7. Задание {{ 7 }} ТЗ № 7
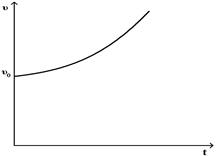
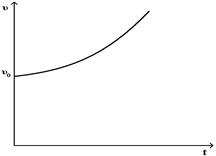
При равноускоренном движении материальной точки зависимость скорости от времени имеет вид
£ 
£ 
R 
£ 
8. Задание {{ 8 }} ТЗ № 8
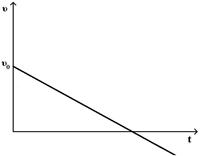
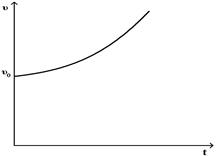
При равнозамедленном движении материальной точки зависимость скорости от времени имеет вид
£ 
R 
£ 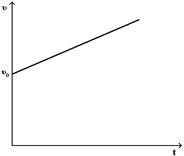
£ 
9. Задание {{ 10 }} ТЗ № 10
Равномерное прямолинейное движение определяется условием
R 
£ 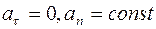
£ 
£ 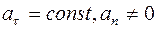
10. Задание {{ 11 }} ТЗ № 11
Равномерное движение по окружности определяется условием
£ 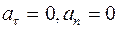
R 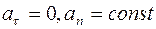
£ 
£ 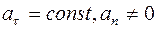
11. Задание {{ 12 }} ТЗ № 12
Равноускоренное прямолинейное движение определяется условием
£ 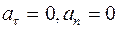
£ 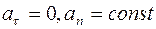
R 
£ 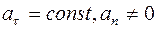
12. Задание {{ 13 }} ТЗ № 13
Равноускоренное движение по окружности определяется условием
£ 
£ 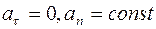
£ 
R 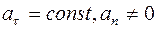
13. Задание {{ 14 }} ТЗ № 14
Связь между линейной и угловой скоростью определяется формулой
R 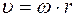
£ 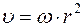
£ 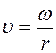
£ 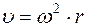
14. Задание {{ 15 }} ТЗ № 15
Связь между тангенциальным и угловым ускорениями определяется формулой
R 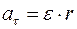
£ 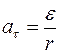
£ 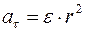
£ 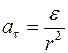
15. Задание {{ 16 }} ТЗ № 16
Связь нормального ускорения с угловой скоростью определяется формулой
R 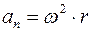
£ 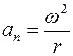
£ 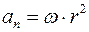
£ 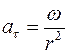
16. Задание {{ 17 }} ТЗ № 17
Автомобиль, трогаясь с места, движется с ускорением 3 м/ 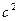 . Через 4 сек. его скорость будет [м/с]
. Через 4 сек. его скорость будет [м/с]
R 12
£ 0.75
£ 24
£ 6
17. Задание {{ 18 }} ТЗ № 18
Скорость тела через 2 сек после начала движения, для которого пройденный путь задается уравнением 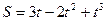 (все величины в СИ), будет равна [м/с]
(все величины в СИ), будет равна [м/с]
£ 12
R 7
£ 14
£ 6
18. Задание {{ 19 }} ТЗ № 19
Зависимость пути от времени для прямолинейно движущегося тела имеет вид 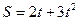 ( все величины даны в СИ). Ускорение тела через 2 сек будет равно [м/
( все величины даны в СИ). Ускорение тела через 2 сек будет равно [м/ 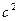 ]
]
R 6
£ 38
£ 30
£ 24
19. Задание {{ 20 }} ТЗ № 20
Зависимость пути от времени для прямолинейно движущегося тела имеет вид 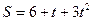 ( все величины даны в СИ). Ускорение тела равно [м/
( все величины даны в СИ). Ускорение тела равно [м/ 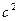 ]
]
£ 1
£ 2
£ 3
R 6
20. Задание {{ 137 }} ТЗ № 137
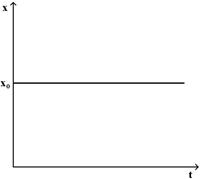
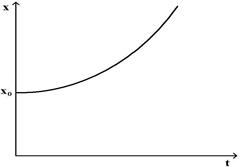
Зависимость координаты от времени при равномерном прямолинейном движении материальной точки имеет вид
£ 
R 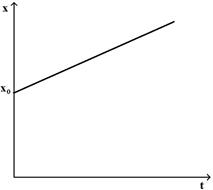
£ 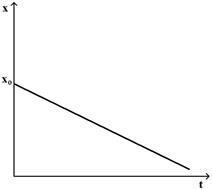
£ 
21. Задание {{ 21 }} ТЗ № 21
Угловая скорость тела через 3 сек после начала движения, если угол поворота задается уравнением 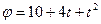 (все величины даны в СИ), будет равна [рад/с]
(все величины даны в СИ), будет равна [рад/с]
R 10
£ 31
£ 22
£ 6
22. Задание {{ 22 }} ТЗ № 22
Угловое ускорение тела через 2 сек после начала движения, если угол поворота задается уравнением 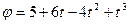 (все величины даны в СИ), будет равно [рад/
(все величины даны в СИ), будет равно [рад/  ]
]
£ 6
£ 8
£ 9
R 4
23. Задание {{ 23 }} ТЗ № 23
От высокой скалы отломился и стал свободно падать камень (g = 10 м/ 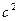 ). Через 3 сек. после начала падения его скорость равна [м/с]
). Через 3 сек. после начала падения его скорость равна [м/с]
£ 3
£ 10
R 30
£ 2
24. Задание {{ 24 }} ТЗ № 24
Две материальные точки движутся по окружностям радиусами 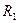 и
и 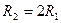 с одинаковыми по модулю скоростями. Их периоды вращения связаны соотношением
с одинаковыми по модулю скоростями. Их периоды вращения связаны соотношением
R 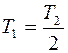
£ 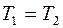
£ 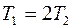
£ 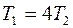
25. Задание {{ 25 }} ТЗ № 25
Зависимость пути от времени для прямолинейно движущегося тела имеет вид  ( все величины даны в СИ). Зависимость скорости от времени имеет вид
( все величины даны в СИ). Зависимость скорости от времени имеет вид
£ 
£ 
R 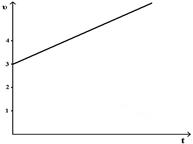
£ 
26. Задание {{ 26 }} ТЗ № 26
Зависимость пути от времени для прямолинейно движущегося тела имеет вид  ( все величины даны в СИ). Зависимость ускорения от времени имеет вид
( все величины даны в СИ). Зависимость ускорения от времени имеет вид
R 
£ 
£ 
£ 
27. Задание {{ 27 }} ТЗ № 27
Материальная точка движется по указанной траектории с постоянной по модулю скоростью
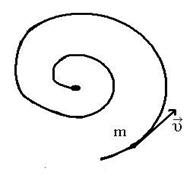
Ускорение при этом
£ равно нулю
£ остается постоянным
R увеличивается
£ уменьшается
28. Задание {{ 28 }} ТЗ № 28
Материальная точка движется по указанной траектории с постоянной по модулю скоростью
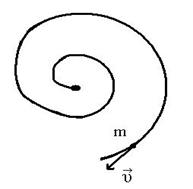
Ускорение при этом
£ равно нулю
£ остается постоянным
£ увеличивается
R уменьшается
29. Задание {{ 29 }} ТЗ № 29
Материальная точка вращается равномерно по окружности по часовой стрелке.
Ускорение при этом направлено вдоль
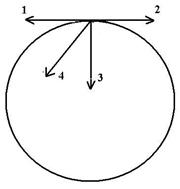
£ 1
£ 2
R 3
£ 4
30. Задание {{ 30 }} ТЗ № 30
Материальная точка вращается равномерно по окружности против часовой стрелки. Ускорение при этом направлено вдоль
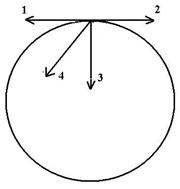
£ 1
£ 2
R 3
£ 4
31. Задание {{ 31 }} ТЗ № 31
Материальная точка вращается равноускоренно по окружности по часовой стрелке. Ускорение при этом направлено вдоль
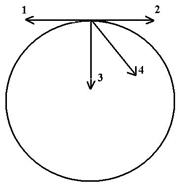
£ 1
£ 2
£ 3
R 4
32. Задание {{ 32 }} ТЗ № 32
Материальная точка вращается равнозамедленно по окружности против часовой стрелки. Ускорение при этом направлено вдоль

£ 1
£ 2
£ 3
R 4
33. Задание {{ 33 }} ТЗ № 33
Два тела массами 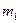 и
и 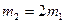 брошены горизонтально с одинаковыми скоростями с высоты h .Времена падения этих тел связаны соотношением
брошены горизонтально с одинаковыми скоростями с высоты h .Времена падения этих тел связаны соотношением
£ 
£ 
R 
£ 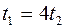
34. Задание {{ 34 }} ТЗ № 34
Два тела массами 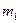 и
и 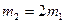 брошены горизонтально с одинаковыми скоростями с высоты h .Дальности падения этих тел связаны соотношением
брошены горизонтально с одинаковыми скоростями с высоты h .Дальности падения этих тел связаны соотношением
£ 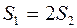
£ 
R 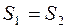
£ 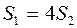
35. Задание {{ 35 }} ТЗ № 35
Период вращения – это
R время, за которое тело совершает один полный оборот
£ число оборотов за единицу времени
£ полное время вращения тела
£ число оборотов за все время вращения тела
36. Задание {{ 36 }} ТЗ № 36
Частота вращения - это
£ время, за которое тело совершает один полный оборот
R число оборотов за единицу времени
£ полное время вращения тела
£ число оборотов за все время вращения тела
37. Задание {{ 37 }} ТЗ № 37
Частота определяется формулой
£ 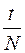
R 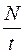
£ 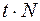
£ 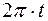
38. Задание {{ 38 }} ТЗ № 38
Зависимость угла поворота от времени для вращающегося тела задается уравнением  (все величины даны в СИ). Угловое ускорение тела через 3 сек. после начала движения будет равна [рад/с
(все величины даны в СИ). Угловое ускорение тела через 3 сек. после начала движения будет равна [рад/с 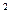 ]
]
£ 4
£ 6
R 2
£ 31
39. Задание {{ 39 }} ТЗ № 39
Тело равномерно вращается по окружности радиусом два метра с угловой скоростью 70 рад/с. Ускорение тела равно [м/ 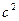 ]
]
£ 140
£ 35
£ 2450
R 9800
40. Задание {{ 40 }} ТЗ № 40
Зависимость угла поворота от времени для вращающегося тела имеет вид 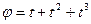 (все величины даны в СИ). Радиус вращения тела 10 см. Тангенциальное ускорение к концу третьей секунды равно [м/
(все величины даны в СИ). Радиус вращения тела 10 см. Тангенциальное ускорение к концу третьей секунды равно [м/ 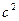 ]
]
R 2
£ 3
£ 18
£ 200
41. Задание {{ 41 }} ТЗ № 41
Зависимость угла поворота от времени для вращающегося тела имеет вид 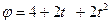 (все величины даны в СИ). Радиус вращения тела 10 см. Нормальное ускорение к концу второй секунды равно [м/
(все величины даны в СИ). Радиус вращения тела 10 см. Нормальное ускорение к концу второй секунды равно [м/ 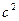 ]
]
R 10
£ 16
£ 100
£ 1000
42. Задание {{ 42 }} ТЗ № 42
Зависимость угла поворота от времени для вращающегося тела имеет вид 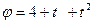 (все величины даны в СИ). Радиус вращения тела 1 м. Ускорение тела к концу первой секунды равно [м/
(все величины даны в СИ). Радиус вращения тела 1 м. Ускорение тела к концу первой секунды равно [м/ 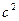 ]
]
£ 2
£ 3
£ 9
R 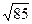
Механика твердого тела
103. Задание {{ 103 }} ТЗ № 103
Момент силы твердого тела определяется формулой
£ 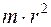
£ 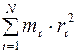
£ 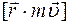
R 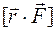
104. Задание {{ 104 }} ТЗ № 104
Момент импульса твердого тела определяется формулой
£ 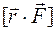
£ 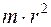
£ 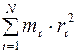
R 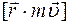
105. Задание {{ 105 }} ТЗ № 105
Момент инерции твердого тела определяется формулой
£ 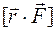
£ 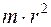
R 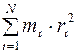
£ 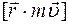
106. Задание {{ 106 }} ТЗ № 106
Момент инерции материальной точки определяется формулой
£ 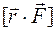
R 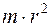
£ 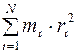
£ 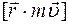
107. Задание {{ 107 }} ТЗ № 107
Основное уравнение динамики вращательного движения имеет вид
R 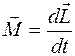
£ 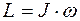
£ 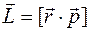
108. Задание {{ 108 }} ТЗ № 108
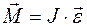
£ 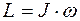
£ 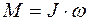
£ 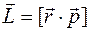
109. Задание {{ 109 }} ТЗ № 109
Момент импульса равен
£ 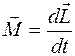
R 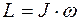
£ 
£
110. Задание {{ 110 }} ТЗ № 110
Закон сохранения момента импульса имеет вид
£ 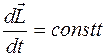
£ 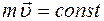
£ 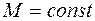
R 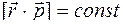
111. Задание {{ 111 }} ТЗ № 111
Кинетическая энергия вращательного движения равна
£ 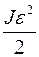
R 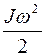
£ 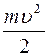
£ 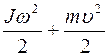
112. Задание {{ 112 }} ТЗ № 112
Кинетическая энергия одновременного поступательного и вращательного движения равна
£ 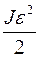
£ 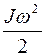
£ 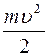
R 
113. Задание {{ 113 }} ТЗ № 113
Момент инерции тонкого стержня относительно оси, проходящей через его середину и перпендикулярной к ней, равен
£ 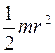
R 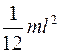
£ 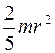
£ 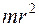
114. Задание {{ 114 }} ТЗ № 114
Момент инерции диска относительно оси, проходящей через центр массы перпендикулярно диску, равен
R 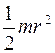
£ 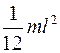
£ 
£ 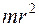
115. Задание {{ 115 }} ТЗ № 115
Момент инерции полого цилиндра равен
£ 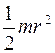
£ 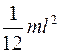
£ 
R 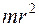
116. Задание {{ 116 }} ТЗ № 116
Момент инерции шара равен
£ 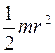
£ 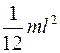
R Момент инерции диска относительно оси , проходящей касательно к его поверхности через конец радиуса, равен
£ 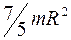
R 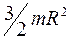
£ 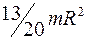
118. Задание {{ 118 }} ТЗ № 118
Момент инерции стержня относительно оси, проходящей через точку, находящуюся на расстоянии 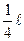 от конца, равен
от конца, равен
R 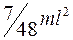
£ 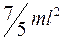
£ 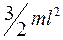
£ 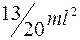
119. Задание {{ 119 }} ТЗ № 119
Момент инерции шара, относительно оси, проходящей через середину радиуса, равен
£ 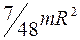
£ 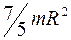
£ 
R 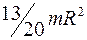
120. Задание {{ 120 }} ТЗ № 120
Момент инерции шара относительно оси, касательной к его поверхности, равен
£ 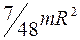
R 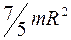
£ 
£ 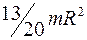
121. Задание {{ 121 }} ТЗ № 121
Момент импульса относительно неподвижной оси изменяется по закону 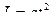 . Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело
. Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело
£ 
R 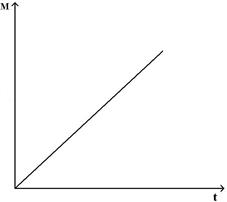
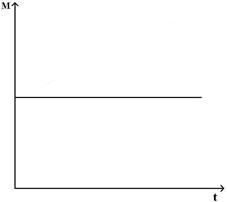
£ 
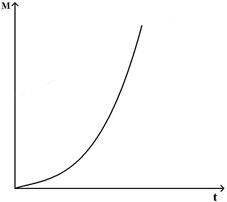
£ 
122. Задание {{ 122 }} ТЗ № 122
Момент импульса относительно неподвижной оси изменяется по закону 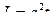 . Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело
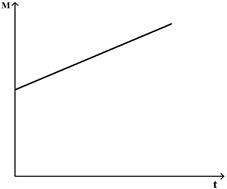
. Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело
£ 
£ 
R 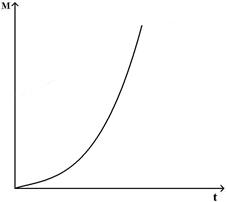
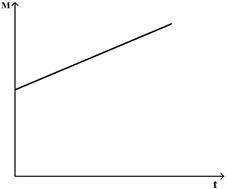
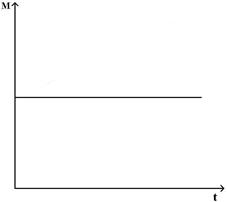
123. Задание {{ 123 }} ТЗ № 123
Момент импульса относительно неподвижной оси изменяется по закону 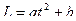 . Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело
. Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело
£ 
R 
£ 
£ 
124. Задание {{ 124 }} ТЗ № 124
Момент импульса относительно неподвижной оси изменяется по закону 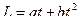 . Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело
. Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело
R 
£ 
£ 
£ 
125. Задание {{ 125 }} ТЗ № 125
Момент импульса относительно неподвижной оси изменяется по закону 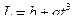 . Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело
. Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело
£ 
£ 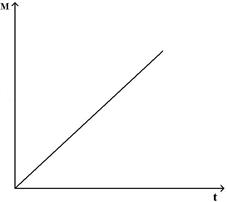
£ 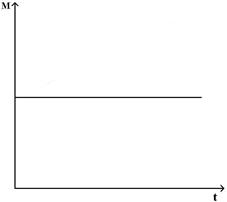
R 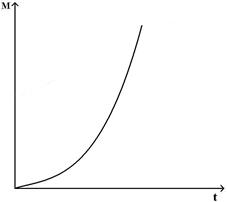
126. Задание {{ 126 }} ТЗ № 126
Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания на горку. Если начальные скорости тел одинаковы, то
R выше поднимется полый шар
£ оба тела поднимутся на одну и ту же высоту
£ выше поднимется сплошной цилиндр
127. Задание {{ 127 }} ТЗ № 127
Диск массой 5 кг катится без скольжения по горизонтальной плоскости со скоростью 4 м/с. Кинетическая энергия диска равна [Дж]
£ 40
R 60
£ 80
£ 120
128. Задание {{ 128 }} ТЗ № 128
Шар массой 5 кг катится без скольжения по горизонтальной плоскости со скоростью 4 м/с. Кинетическая энергия шара равна [Дж]
R 56
£ 40
£ 50
£ 20
129. Задание {{ 129 }} ТЗ № 129
Полый цилиндр массой 4 кг катится без скольжения по горизонтальной плоскости со скоростью 2 м/с. Кинетическая энергия цилиндра равна [Дж]
£ 8
£ 12
R 16
£ 24
130. Задание {{ 130 }} ТЗ № 130
Тонкостенный шар 2 кг катится без скольжения по горизонтальной плоскости со скоростью 3 м/с. Кинетическая энергия шара равна [Дж]
£ 13,5
£ 9
£ 6
R 15
131. Задание {{ 131 }} ТЗ № 131
Радиус шара в 2 раза больше радиуса цилиндра, а их массы равны. Для их моментов инерции 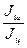 справедливо соотношение
справедливо соотношение
R 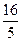
£ 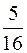
£ 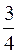
£ 
132. Задание {{ 132 }} ТЗ № 132
При увеличении угловой скорости вращения шара в 3 раза, его кинетическая энергия
R увеличится в 9 раз
£ уменьшится в 9 раз
£ не изменится
£ увеличится в 3 раза
133. Задание {{ 133 }} ТЗ № 133
При уменьшении момента инерции тела в 4 раза, его кинетическая энергия вращения при неизменной угловой скорости
R уменьшится в 4 раза
£ уменьшится в 16 раз
£ увеличится в 4 раза
£ не изменится
134. Задание {{ 134 }} ТЗ № 134
При увеличении в 2 раза радиуса шара и уменьшении его массы в 2 раза момент инерции
£ уменьшится в 2 раза
R увеличится в 2 раза
£ уменьшится в 4 раза
£ не изменится
135. Задание {{ 135 }} ТЗ № 135
Радиус шара массой 2 кг, у которого момент инерции 5 кг м  , равен [м]
, равен [м]
R 2,5
£ 5
£ 10
£ 10,5
136. Задание {{ 136 }} ТЗ № 136
Момент инерции сплошного цилиндра массой 5 кг и радиусом 20 см , относительно оси проходящей через его центр равен
R 0,1
£ 1
£ 10
£ 100
Механика жидкостей
149. Задание {{ 150 }} ТЗ № 150
Условие плавания тела в жидкости определяется
£ объёмом тела
£ массой тела
£ формой и массой тела
R соотношением плотностей тела и жидкости
150. Задание {{ 151 }} ТЗ № 151
Тело плавает в керосине ( 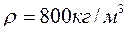 ) погружаясь на половину своего объема. Часть объёма этого же тела, погруженного в воду, будет
) погружаясь на половину своего объема. Часть объёма этого же тела, погруженного в воду, будет
£ 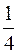
£ 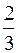
£ 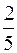
151. Задание {{ 152 }} ТЗ № 152
Два тела 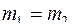 c разной плотностью
c разной плотностью 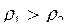 погружены в одну жидкость. Выталкивающие силы будут
погружены в одну жидкость. Выталкивающие силы будут
£ 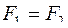
R 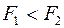
£ 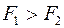
£ 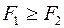
152. Задание {{ 153 }} ТЗ № 153
При уменьшении глубины погружения тела в 3 раза выталкивающая сила
£ уменьшилась в 3 раза
£ увеличилась в 3 раза
£ уменьшилась в 9 раз
R не изменилась
153. Задание {{ 154 }} ТЗ № 154
На тело объёмом 2м 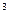 и плотностью 500 кг/м
и плотностью 500 кг/м 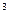 , наполовину погруженное в воду плотностью 10
, наполовину погруженное в воду плотностью 10 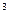 кг/м
кг/м 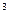 , действует сила Архимеда, которая равна
, действует сила Архимеда, которая равна
R 20кН
£ 5кН
£ 2кН
154. Задание {{ 155 }} ТЗ № 155
выше на 3см
£ выше на 3,5см
R ниже на 3см
£ Гидростатическое давление жидкости равно
£ 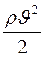
£ 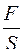
£ 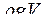
R 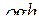
156. Задание {{ 157 }} ТЗ № 157
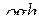
R 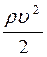
£ 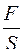
£ 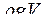
157. Задание {{ 158 }} ТЗ № 158
Глубина озера, где гидростатическое давление воды (с учётом атмосферного) 5*10 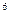 Па, будет равна [м]
Па, будет равна [м]
£ 500
£ 510
R 50
158. Задание {{ 159 }} ТЗ № 159
Глубина озера, где гидростатическое давление воды (без учета атмосферного) 4*10 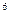 Па будет равна [м]
Па будет равна [м]
£ 4000
R 400
£ 40
£ 4
159. Задание {{ 160 }} ТЗ № 160
Бак высотой 2 м заполнен водой. На малое отверстие в баке на высоте 0,5 м от основания действует давление (с учетом атмосферного) кПа
£ 1
£ 1,5
£ 15
R 115
160. Задание {{ 161 }} ТЗ № 161
Если к малому поршню площадью 25см 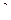 приложена сила 200Н, то на большой поршень площадью 0,1м
приложена сила 200Н, то на большой поршень площадью 0,1м 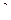 действует сила
действует сила
£ 2 Н
£ 5 Н
£ 500 Н
R 8000 Н
161. Задание {{ 162 }} ТЗ № 162
Жидкость, плотность которой не зависит от давления, является
£ реальной
£ идеальной
£ стационарно текущей
R несжимаемой
162. Задание {{ 163 }} ТЗ № 163
Жидкость, скорость которой в каждой её точке не изменяется, является
£ идеальной
R стационарно текущей
£ несжимаемой
163. Задание {{ 164 }} ТЗ № 164
Жидкость, внутренним трением в которой можно пренебречь, является
£ несжимаемой
R идеальной
£ стационарно текущей
£ реальной
164. Задание {{ 165 }} ТЗ № 165
Вязкость- это свойство жидкости
£ стационарно текущей
R реальной
£ несжимаемой
165. Задание {{ 166 }} ТЗ № 166
Уравнение неразрывности для несжимаемой жидкости имеет вид
£ 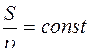
£ 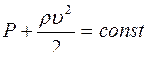
R 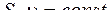
£ 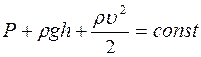
166. Задание {{ 167 }} ТЗ № 167
Уравнение Бернулли для стационарно текущей идеальной жидкости имеет вид
R 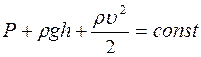
£ 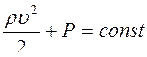
£ 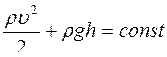
£ 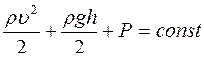
167. Задание {{ 168 }} ТЗ № 168
Уравнение Бернулли в горизонтальной трубке тока имеет вид
R 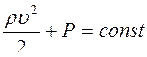
£ 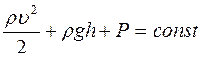
£ 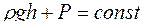
168. Задание {{ 169 }} ТЗ № 169
Скорость истечения жидкости через малое отверстие в стенке равно
£ 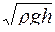
£ 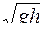
R 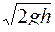
£ 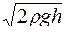
169. Задание {{ 170 }} ТЗ № 170
При переходе воды из одной трубы в другую, диаметр которой в 2 раза меньше, скорость течения
£ уменьшается в 2 раза
£ уменьшается в 4 раза
£ увеличивается в 2 раза
R увеличивается в 4 раза
170. Задание {{ 171 }} ТЗ № 171
При переходе воды из квадратной трубы со стороной в 1м в круглую с радиусом 1м скорость течения
£ не изменилась
£ увеличилась в 3,14 раз
R уменьшилась в 3,14 раз
£ увеличилась в 2 раза
171. Задание {{ 172 }} ТЗ № 172
Скорость течения воды увеличилась в 9 раз при переходе из одной трубы в другую, диаметр которой
£ увеличился в 9 раз
£ уменьшился в 9 раз
£ увеличился в 3 раза
R уменьшился в 3 раза
172. Задание {{ 173 }} ТЗ № 173
Скорость течения воды в широкой части трубы 20см/с. При уменьшении диаметра трубы в 1,5 раза скорость воды будет равна (см/с)
£ 30
£ 1,33
£ 60
R 45
173. Задание {{ 174 }} ТЗ № 174
Разность уровней  жидкостей в одинаковых манометрических трубках 10см. Скорость течения жидкостей по горизонтальной трубе равна [м/с]
жидкостей в одинаковых манометрических трубках 10см. Скорость течения жидкостей по горизонтальной трубе равна [м/с]

£ 1
£ 2
£ 3
R 1,4
174. Задание {{ 175 }} ТЗ № 175
По горизонтальной трубе течет жидкость со скоростью 1 м/с. Разность уровней  жидкости в манометрических трубках одинакового диаметра [cм]
жидкости в манометрических трубках одинакового диаметра [cм]

£ 2
R 5
£ 10
£ 12
175. Задание {{ 176 }} ТЗ № 176
Высота уровня жидкости над отверстием в стенке сосуда 1,8 м. Скорость истечения жидкости из малого отверстия равна [м/с]
£ 4,2
R 6
£ 3
£ 2,5
176. Задание {{ 177 }} ТЗ № 177
Закон Ньютона для вязкости имеет вид
£ 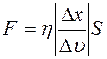
R 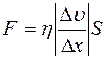
£ 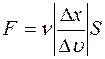
£ 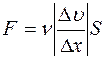
177. Задание {{ 178 }} ТЗ № 178
Вязкость в метоле Стокса определяется по формуле
£ 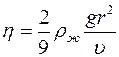
£ 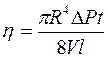
R 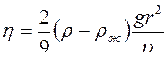
£ 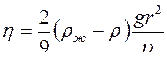
178. Задание {{ 179 }} ТЗ № 179
Вязкость в методе Пуазеля определяется по формуле
£ 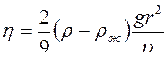
£ 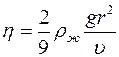
£ 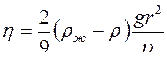
R 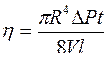
179. Задание {{ 180 }} ТЗ № 180
Характер течения жидкости определяется безразмерной величиной
R 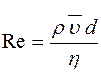
£ 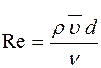
£ 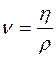
£ 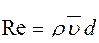
180. Задание {{ 181 }} ТЗ № 181
Число Рейнольдса зависит от
£ массы
£ давления
R вязкости
£ объема
181. Задание {{ 182 }} ТЗ № 182
Ламинарное течение наблюдается при значениях числа Рейнольдса
£ 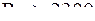
R 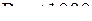
£ 
£ 
182. Задание {{ 183 }} ТЗ № 183
Переход от ламинарного течения к турбулентному наблюдается при значениях числа Рейнольдса
£ 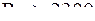
£ 
£ 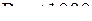
R 
183. Задание {{ 184 }} ТЗ № 184
Турбулентное течение наблюдается при значениях числа Рейнольдса
£ 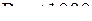
R 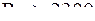
£ 
£ 
Основы термодинамики
315. Задание {{ 316 }} ТЗ № 316
Первое начало термодинамики имеет вид
R 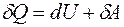
£ 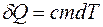
£ 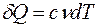
£ 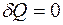
316. Задание {{ 317 }} ТЗ № 317
Первое начало термодинамики при изохорном процессе имеет вид
R 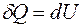
£ 
£ 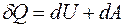
£ 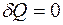
317. Задание {{ 318 }} ТЗ № 318
Первое начало термодинамики при изобарном процессе имеет вид
£ 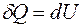
£ 
R 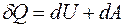
£ 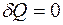
318. Задание {{ 319 }} ТЗ № 319
Первое начало термодинамики при изотермическом процессе имеет вид
£ 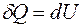
R 
£ 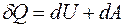
£ 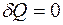
319. Задание {{ 320 }} ТЗ № 320
Молярная теплоемкость равна
£ 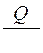
R 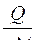
£ 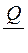
£ 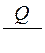
320. Задание {{ 321 }} ТЗ № 321
Удельная теплоемкость вещества равна
R 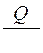
£ 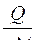
£ 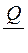
£ Уравнение политропного процесса имеет вид
£ 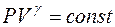
£ 
R 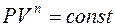
£ 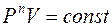
322. Задание {{ 343 }} ТЗ № 343
Работа газа при изменении его объема равна
£ 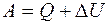
£ 
R 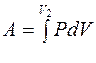
£ 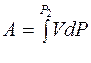
323. Задание {{ 344 }} ТЗ № 344
Работа, совершаемая газом при изохорном процессе
£ 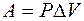
R 
£ 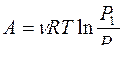
£ 
324. Задание {{ 345 }} ТЗ № 345
Работа, совершаемая газом при изотермическом процессе равна
£ 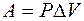
£ 
R 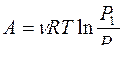
£ 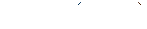
325. Задание {{ 346 }} ТЗ № 346
Работа, совершаемая газом при изобарном процессе равна
£ 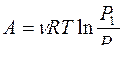
£ 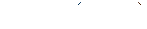
R 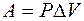
£ 
326. Задание {{ 347 }} ТЗ № 347
Работа, совершаемая газом при адиабатном процессе равна
£ 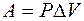
£ 
£ 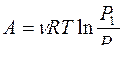
R 
327. Задание {{ 348 }} ТЗ № 348
Внутренняя энергия на каждую поступательную и вращательную степень свободы равна
£ 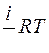
£ 
R 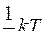
£ 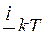
328. Задание {{ 349 }} ТЗ № 349
Внутренняя энергия одной молекулы равна
£ 
R 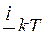
£ 
£ 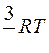
329. Задание {{ 350 }} ТЗ № 350
Внутренняя энергия 1 моля газа равна
£ 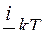
R 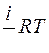
£ 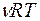
£ 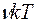
330. Задание {{ 351 }} ТЗ № 351
Внутренняя энергия произвольного количества газа равна
£ 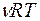
£ 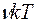
£ 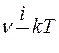
R 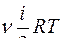
331. Задание {{ 352 }} ТЗ № 352
При повышении термодинамической температуры идеального газа в 3 раза его внутренняя энергия
£ не изменится
£ увеличится в 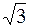 раз
раз
R увеличится в 3 раза
£ увеличится в 9 раз
332. Задание {{ 353 }} ТЗ № 353
Внутренняя энергия тела изменится, если
R его нагреть или охладить
£ изменить скорость тела
£ поднять тело над поверхностью Земли
£ действуют внешние силы
333. Задание {{ 354 }} ТЗ № 354
10 молей аргона нагрели при постоянном объеме от 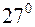 С до
С до 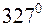 С. Внутренняя энергия газа увеличилась в
С. Внутренняя энергия газа увеличилась в
£ 1.5 раз
R 2 раза
£ 3 раза
£ 12.1 раз
334. Задание {{ 355 }} ТЗ № 355
Внутренняя энергия газа в процессе, изображенном на рисунке

£ не изменится
R увеличивается
£ уменьшится
£ равна нулю
335. Задание {{ 356 }} ТЗ № 356
Внутренняя энергия идеального одноатомного газа в сосуде объемом 0.5 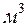 под давлением
под давлением 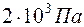 равна [кДж]
равна [кДж]
£ 1
£ 0.5
R 1.5
£ 3
336. Задание {{ 357 }} ТЗ № 357
 На рисунке показан круговой цикл из четырех изопроцессов. Внутренняя энергия уменьшается на участке
На рисунке показан круговой цикл из четырех изопроцессов. Внутренняя энергия уменьшается на участке
£ 1-2
£ 2-3
R 3-4
£ 4-1
337. Задание {{ 358 }} ТЗ № 358
 Работа газа за весь цикл изображенный на рисунке равна
Работа газа за весь цикл изображенный на рисунке равна
£ 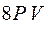
£ 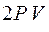
R 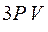
£ 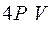
338. Задание {{ 359 }} ТЗ № 359
 Работа 1 моля идеального одноатомного газа в процессе, изображенном на рисунке
Работа 1 моля идеального одноатомного газа в процессе, изображенном на рисунке
равна
£ 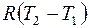
R 
£ 
£ 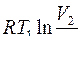
339. Задание {{ 360 }} ТЗ № 360
 При переходе идеального газа из состояния А и состояние В газ совершает наибольшую работу в случае
При переходе идеального газа из состояния А и состояние В газ совершает наибольшую работу в случае
R 1
£ 2
£ 3
£ 1 и 3
340. Задание {{ 361 }} ТЗ № 361
Идеальный газ получил количество теплоты 100 Дж, при этом его внутренняя энергия увеличилась на 100 Дж. Работа совершенная газом равна [Дж]
£ -200
R 0
£ 100
£ 200
341. Задание {{ 322 }} ТЗ № 322
Теплоемкость тела равна
£ 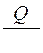
£ 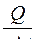
R 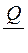
£ 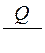
342. Задание {{ 323 }} ТЗ № 323
Уравнение Майера
£ 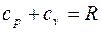
R 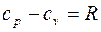
£ 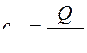
£ 
343. Задание {{ 324 }} ТЗ № 324
Число степеней свободы одноатомного газа равно
R 3
£ 4
£ 5
£ 6
344. Задание {{ 325 }} ТЗ № 325
Число степеней свободы двухатомного газа равно
£ 3
£ 4
R 5
£ 6
345. Задание {{ 326 }} ТЗ № 326
Число степеней свободы трехатомного газа равно
£ 3
£ 4
£ 5
R 6
346. Задание {{ 327 }} ТЗ № 327
Число степеней свободы многоатомного газа равно
£ 3
£ 4
£ 5
R 6
347. Задание {{ 328 }} ТЗ № 328
Число степеней свободы молекулы кислорода равно
£ 3
R 5
£ 6
£ 7
348. Задание {{ 329 }} ТЗ № 329
Число степеней свободы атома водорода равно
R 3
£ 5
£ 6
£ 1
349. Задание {{ 330 }} ТЗ № 330
Число степеней свободы молекулы водорода равно
£ 1
£ 3
R 5
£ 6
350. Задание {{ 331 }} ТЗ № 331
Число степеней свободы молекулы воды равно
£ 1
£ 3
£ 5
R 6
351. Задание {{ 332 }} ТЗ № 332
Теплоемкость тела при постоянном объеме равна
R 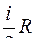
£ 
£ 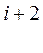
£ 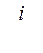
352. Задание {{ 333 }} ТЗ № 333
Теплоемкость тела при постоянном давлении равна
£ 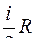
R 
£ 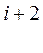
£ 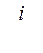
353. Задание {{ 334 }} ТЗ № 334
Теплоемкость одноатомного газа при постоянном давлении 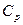 равна
равна
£ 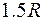
R 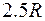
£ 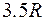
£ 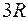
354. Задание {{ 335 }} ТЗ № 335
Теплоемкость двухатомного газа при постоянном объеме 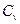 равна
равна
£ 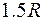
R 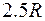
£ 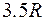
£ 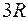
355. Задание {{ 336 }} ТЗ № 336
Коэффициент Пуассона 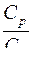 равен
равен
£ 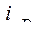
£ 
R 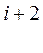
£ 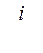
356. Задание {{ 337 }} ТЗ № 337
Отношение теплоемкостей 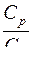 для двухатомного газа равно
для двухатомного газа равно
£ 1
R 1.4
£ 2
£ 2.5
357. Задание {{ 338 }} ТЗ № 338
Адиабатический процесс – это процесс, при котором
£ 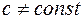
R 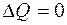
£ 
£ 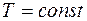
358. Задание {{ 339 }} ТЗ № 339
Уравнение адиабаты имеет вид
R 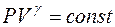
£ 
£ 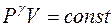
£ 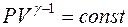
359. Задание {{ 340 }} ТЗ № 340
Уравнение адиабаты имеет вид
R 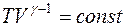
£ 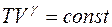
£ 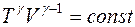
360. Задание {{ 341 }} ТЗ № 341
Политропный процесс – это процесс, при котором
R 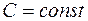
£ 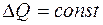
£ 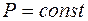
£ 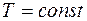
361. Задание {{ 362 }} ТЗ № 362
Все реальные процессы
£ обратимые
R необратимые
£ круговые
£ адиабатные
362. Задание {{ 363 }} ТЗ № 363
В результате циклического процесса газ вернулся в исходное состояние, значит
£ 
£ 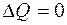
£ 
R 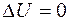
363. Задание {{ 364 }} ТЗ № 364
Цикл Карно состоит из
R двух изотерм и двух адиабат
£ двух изобар и двух адиабат
£ двух изохор и двух адиабат
£ двух изотерм и двух изохор
364. Задание {{ 365 }} ТЗ № 365
КПД идеальной тепловой машины равен
R 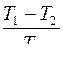
£ 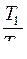
£ 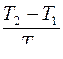
£ 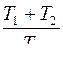
365. Задание {{ 366 }} ТЗ № 366
Энтропия системы – это функция состояния, дифференциал которой равен
R 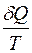
£ 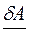
£ 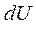
£ 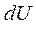
366. Задание {{ 367 }} ТЗ № 367
Изменение энтропии системы при 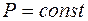
R 
£ 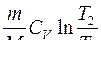
£ 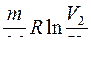
£ 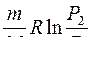
367. Задание {{ 368 }} ТЗ № 368
Изменение энтропии системы при 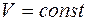
£ 
R 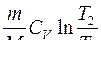
£ 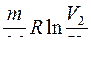
£ 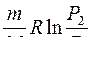
368. Задание {{ 369 }} ТЗ № 369
Изменение энтропии системы при 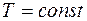
£ 
£ 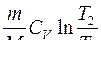
R 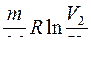
£ 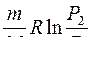
369. Задание {{ 370 }} ТЗ № 370
В замкнутой системе изменение энтропии при обратимом процессе будет
R 0
£ >0
£ <0
£ 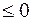
370. Задание {{ 371 }} ТЗ № 371
>0
£ 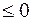
СОДЕРЖАНИЕ И СТРУКТУРА ТЕСТОВЫХ МАТЕРИАЛОВ
Тематическая структура
Тема
Элементы кинематики
Динамика материальной точки и поступательного движения твердых тел
Энергия. Работа. Мощность. Законы сохранения в механике
Механика твердого тела
Неинерциальные системы отсчета
Механика жидкостей
Механические колебания и волны
Специальная теория относительности
Молекулярно-кинетическая теория идеальных газов
Основы термодинамики
Реальные газы, жидкости и твердые тела
СОДЕРЖАНИЕ ТЕСТОВЫХ МАТЕРИАЛОВ
Элементы кинематики
1. Задание {{ 1 }} ТЗ № 1
Путь при равномерном прямолинейном движении определяется по формуле
R 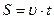
£ 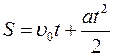
£ 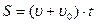
£ 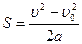
2. Задание {{ 2 }} ТЗ № 2
Путь при равноускоренном прямолинейном движении определяется по формуле
£ 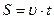
R 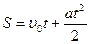
£ 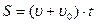
£ 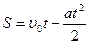
3. Задание {{ 3 }} ТЗ № 3
Путь при равнозамедленном прямолинейном движении определяется по формуле
£ 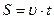
£ 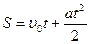
£ 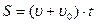
R 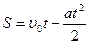
4. Задание {{ 4 }} ТЗ № 4
Мгновенное значение скорости определяется формулой
R 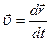
£ 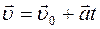
£ 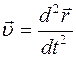
£ 
5. Задание {{ 5 }} ТЗ № 5
Мгновенное значение ускорения определяется формулой
£ 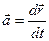
R 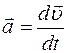
£ 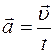
£ 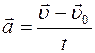
6. Задание {{ 6 }} ТЗ № 6
При равномерном движении материальной точки зависимость скорости от времени имеет вид
R 
£ 
£ 
£ 
7. Задание {{ 7 }} ТЗ № 7
При равноускоренном движении материальной точки зависимость скорости от времени имеет вид
£ 
£ 
R 
£ 
8. Задание {{ 8 }} ТЗ № 8
При равнозамедленном движении материальной точки зависимость скорости от времени имеет вид
£ 
R 
£ 
£ 
9. Задание {{ 10 }} ТЗ № 10
Равномерное прямолинейное движение определяется условием
R 
£ 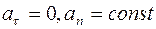
£ 
£ 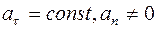
10. Задание {{ 11 }} ТЗ № 11
Равномерное движение по окружности определяется условием
£ 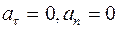
R 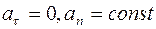
£ 
£ 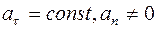
11. Задание {{ 12 }} ТЗ № 12
Равноускоренное прямолинейное движение определяется условием
£ 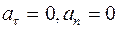
£ 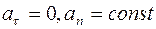
R 
£ 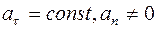
12. Задание {{ 13 }} ТЗ № 13
Равноускоренное движение по окружности определяется условием
£ 
£ 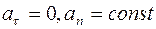
£ 
R 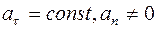
13. Задание {{ 14 }} ТЗ № 14
Связь между линейной и угловой скоростью определяется формулой
R 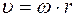
£ 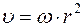
£ 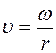
£ 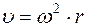
14. Задание {{ 15 }} ТЗ № 15
Связь между тангенциальным и угловым ускорениями определяется формулой
R 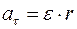
£ 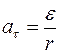
£ 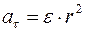
£ 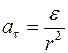
15. Задание {{ 16 }} ТЗ № 16
Связь нормального ускорения с угловой скоростью определяется формулой
R 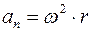
£ 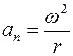
£ 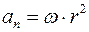
£ 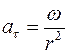
16. Задание {{ 17 }} ТЗ № 17
Автомобиль, трогаясь с места, движется с ускорением 3 м/ 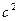 . Через 4 сек. его скорость будет [м/с]
. Через 4 сек. его скорость будет [м/с]
R 12
£ 0.75
£ 24
£ 6
17. Задание {{ 18 }} ТЗ № 18
Скорость тела через 2 сек после начала движения, для которого пройденный путь задается уравнением 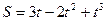 (все величины в СИ), будет равна [м/с]
(все величины в СИ), будет равна [м/с]
£ 12
R 7
£ 14
£ 6
18. Задание {{ 19 }} ТЗ № 19
Зависимость пути от времени для прямолинейно движущегося тела имеет вид 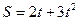 ( все величины даны в СИ). Ускорение тела через 2 сек будет равно [м/
( все величины даны в СИ). Ускорение тела через 2 сек будет равно [м/ 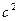 ]
]
R 6
£ 38
£ 30
£ 24
19. Задание {{ 20 }} ТЗ № 20
Зависимость пути от времени для прямолинейно движущегося тела имеет вид 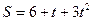 ( все величины даны в СИ). Ускорение тела равно [м/
( все величины даны в СИ). Ускорение тела равно [м/ 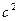 ]
]
£ 1
£ 2
£ 3
R 6
20. Задание {{ 137 }} ТЗ № 137
Зависимость координаты от времени при равномерном прямолинейном движении материальной точки имеет вид
£ 
R 
£ 
£ 
21. Задание {{ 21 }} ТЗ № 21
Угловая скорость тела через 3 сек после начала движения, если угол поворота задается уравнением 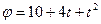 (все величины даны в СИ), будет равна [рад/с]
(все величины даны в СИ), будет равна [рад/с]
R 10
£ 31
£ 22
£ 6
22. Задание {{ 22 }} ТЗ № 22
Угловое ускорение тела через 2 сек после начала движения, если угол поворота задается уравнением 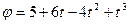 (все величины даны в СИ), будет равно [рад/
(все величины даны в СИ), будет равно [рад/  ]
]
£ 6
£ 8
£ 9
R 4
23. Задание {{ 23 }} ТЗ № 23
От высокой скалы отломился и стал свободно падать камень (g = 10 м/ 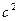 ). Через 3 сек. после начала падения его скорость равна [м/с]
). Через 3 сек. после начала падения его скорость равна [м/с]
£ 3
£ 10
R 30
£ 2
24. Задание {{ 24 }} ТЗ № 24
Две материальные точки движутся по окружностям радиусами 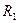 и
и 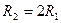 с одинаковыми по модулю скоростями. Их периоды вращения связаны соотношением
с одинаковыми по модулю скоростями. Их периоды вращения связаны соотношением
R 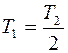
£ 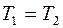
£ 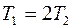
£ 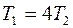
25. Задание {{ 25 }} ТЗ № 25
Зависимость пути от времени для прямолинейно движущегося тела имеет вид  ( все величины даны в СИ). Зависимость скорости от времени имеет вид
( все величины даны в СИ). Зависимость скорости от времени имеет вид
£ 
£ 
R 
£ 
26. Задание {{ 26 }} ТЗ № 26
Зависимость пути от времени для прямолинейно движущегося тела имеет вид  ( все величины даны в СИ). Зависимость ускорения от времени имеет вид
( все величины даны в СИ). Зависимость ускорения от времени имеет вид
R 
£ 
£ 
£ 
27. Задание {{ 27 }} ТЗ № 27
Материальная точка движется по указанной траектории с постоянной по модулю скоростью

Ускорение при этом
£ равно нулю
£ остается постоянным
R увеличивается
£ уменьшается
28. Задание {{ 28 }} ТЗ № 28
Материальная точка движется по указанной траектории с постоянной по модулю скоростью

Ускорение при этом
£ равно нулю
£ остается постоянным
£ увеличивается
R уменьшается
29. Задание {{ 29 }} ТЗ № 29
Материальная точка вращается равномерно по окружности по часовой стрелке.
Ускорение при этом направлено вдоль

£ 1
£ 2
R 3
£ 4
30. Задание {{ 30 }} ТЗ № 30
Материальная точка вращается равномерно по окружности против часовой стрелки. Ускорение при этом направлено вдоль

£ 1
£ 2
R 3
£ 4
31. Задание {{ 31 }} ТЗ № 31
Материальная точка вращается равноускоренно по окружности по часовой стрелке. Ускорение при этом направлено вдоль

£ 1
£ 2
£ 3
R 4
32. Задание {{ 32 }} ТЗ № 32
Материальная точка вращается равнозамедленно по окружности против часовой стрелки. Ускорение при этом направлено вдоль

£ 1
£ 2
£ 3
R 4
33. Задание {{ 33 }} ТЗ № 33
Два тела массами 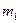 и
и 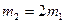 брошены горизонтально с одинаковыми скоростями с высоты h .Времена падения этих тел связаны соотношением
брошены горизонтально с одинаковыми скоростями с высоты h .Времена падения этих тел связаны соотношением
£ 
£ 
R 
£ 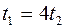
34. Задание {{ 34 }} ТЗ № 34
Два тела массами 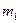 и
и 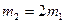 брошены горизонтально с одинаковыми скоростями с высоты h .Дальности падения этих тел связаны соотношением
брошены горизонтально с одинаковыми скоростями с высоты h .Дальности падения этих тел связаны соотношением
£ 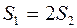
£ 
R 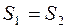
£ 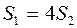
35. Задание {{ 35 }} ТЗ № 35
Период вращения – это
R время, за которое тело совершает один полный оборот
£ число оборотов за единицу времени
£ полное время вращения тела
£ число оборотов за все время вращения тела
36. Задание {{ 36 }} ТЗ № 36
Частота вращения - это
£ время, за которое тело совершает один полный оборот
R число оборотов за единицу времени
£ полное время вращения тела
£ число оборотов за все время вращения тела
37. Задание {{ 37 }} ТЗ № 37
Частота определяется формулой
£ 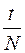
R 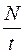
£ 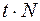
£ 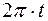
38. Задание {{ 38 }} ТЗ № 38
Зависимость угла поворота от времени для вращающегося тела задается уравнением  (все величины даны в СИ). Угловое ускорение тела через 3 сек. после начала движения будет равна [рад/с
(все величины даны в СИ). Угловое ускорение тела через 3 сек. после начала движения будет равна [рад/с 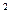 ]
]
£ 4
£ 6
R 2
£ 31
39. Задание {{ 39 }} ТЗ № 39
Тело равномерно вращается по окружности радиусом два метра с угловой скоростью 70 рад/с. Ускорение тела равно [м/ 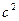 ]
]
£ 140
£ 35
£ 2450
R 9800
40. Задание {{ 40 }} ТЗ № 40
Зависимость угла поворота от времени для вращающегося тела имеет вид 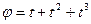 (все величины даны в СИ). Радиус вращения тела 10 см. Тангенциальное ускорение к концу третьей секунды равно [м/
(все величины даны в СИ). Радиус вращения тела 10 см. Тангенциальное ускорение к концу третьей секунды равно [м/ 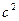 ]
]
R 2
£ 3
£ 18
£ 200
41. Задание {{ 41 }} ТЗ № 41
Зависимость угла поворота от времени для вращающегося тела имеет вид 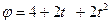 (все величины даны в СИ). Радиус вращения тела 10 см. Нормальное ускорение к концу второй секунды равно [м/
(все величины даны в СИ). Радиус вращения тела 10 см. Нормальное ускорение к концу второй секунды равно [м/ 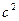 ]
]
R 10
£ 16
£ 100
£ 1000
42. Задание {{ 42 }} ТЗ № 42
Зависимость угла поворота от времени для вращающегося тела имеет вид 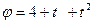 (все величины даны в СИ). Радиус вращения тела 1 м. Ускорение тела к концу первой секунды равно [м/
(все величины даны в СИ). Радиус вращения тела 1 м. Ускорение тела к концу первой секунды равно [м/ 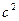 ]
]
£ 2
£ 3
£ 9
R 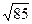
Динамика материальной точки и поступательного движения твердых тел
43. Задание {{ 61 }} ТЗ № 61
При уменьшении расстояния между телами в 5 раз сила тяготения
£ уменьшится в 5 раз
£ увеличится в 5 раз
£ уменьшится в 25 раз
R увеличится в25 раз
44. Задание {{ 62 }} ТЗ № 62
При увеличении масс каждого из двух тел в два раза сила тяготения
£ увеличится в 2 раза
£ уменьшится в 2 раза
R увеличится в 4 раза
£ уменьшится в 4раза
45. Задание {{ 63 }} ТЗ № 63
При увеличении массы одного из тел в 4 раза и увеличении расстояния между ними в 2 раза сила тяготения
£ увеличится в 2 раза
£ увеличится в 4 раза
£ уменьшится в 2 раза
R не изменится
46. Задание {{ 64 }} ТЗ № 64
Космическая ракета удаляется от Земли радиусом R. Сила гравитационного притяжения ракеты Землей уменьшится в 4 раза по сравнению с силой притяжения на земной поверхности на высоте
R R
£ 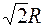
£ 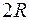
£ 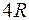
47. Задание {{ 65 }} ТЗ № 65
Мяч массой m брошен вертикально вверх с начальной скоростью 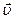 . Если сопротивление воздуха пренебрежимо мало, то изменение импульса мяча за время от начала движения до возвращения в исходную точку равно
. Если сопротивление воздуха пренебрежимо мало, то изменение импульса мяча за время от начала движения до возвращения в исходную точку равно
£ 
£ 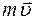
£ 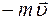
R 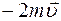
48. Задание {{ 66 }} ТЗ № 66
Тело массой 2 кг движется вдоль оси ОХ. Зависимость координаты от времени имеет вид  ( все величины даны в СИ). В момент времени t =2 с импульс тела равен [кг м/с]
( все величины даны в СИ). В момент времени t =2 с импульс тела равен [кг м/с]
R 46
£ 48
£ 26
£ 86
49. Задание {{ 67 }} ТЗ № 67
Тело движется прямолинейно под действием постоянной силы 5 н. Импульс тела уменьшается от 25 кг м/с до 15 кг м/с за время [с]
£ 1
R 2
£ 3
£ 4
50. Задание {{ 68 }} ТЗ № 68
Тело движется прямолинейно под действием постоянной силы 10 н. Начальный импульс тела равен 50 кг м/с. За 2 сек. он уменьшился и стал равным [кг м/с]
£ 10
£ 20
R 30
£ 40
51. Задание {{ 69 }} ТЗ № 69
Тело движется прямолинейно под действием постоянной силы 4 н и за 2 сек его импульс увеличился и стал равен 20 кг м/с. Первоначальный импульс тела был равен [кг м/с]
£ 4
£ 8
R 12
£ 28
52. Задание {{ 70 }} ТЗ № 70
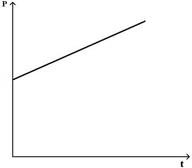 Зависимость импульса от времени прямолинейно движущегося тела представлена на графике. Зависимость равнодействующей силы от времени имеет вид
Зависимость импульса от времени прямолинейно движущегося тела представлена на графике. Зависимость равнодействующей силы от времени имеет вид
£ 
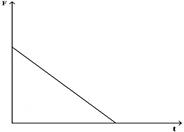
£ 
£ 
R 
53. Задание {{ 71 }} ТЗ № 71
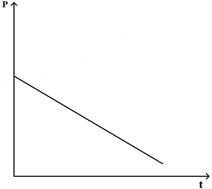 Зависимость импульса от времени прямолинейно движущегося тела представлена на графике. Зависимость равнодействующей силы от времени имеет вид
Зависимость импульса от времени прямолинейно движущегося тела представлена на графике. Зависимость равнодействующей силы от времени имеет вид
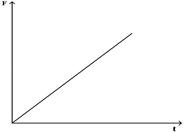
£ 
£ 
R 
£ 
54. Задание {{ 72 }} ТЗ № 72
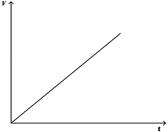
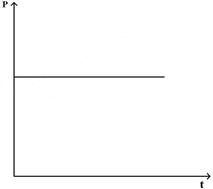 Зависимость импульса от времени прямолинейно движущегося тела представлена на графике. Зависимость равнодействующей силы от времени имеет вид
Зависимость импульса от времени прямолинейно движущегося тела представлена на графике. Зависимость равнодействующей силы от времени имеет вид
£ 
R 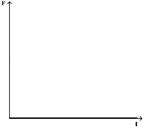
£ 
£ 
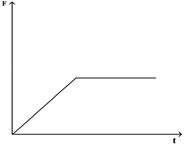
55. Задание {{ 73 }} ТЗ № 73
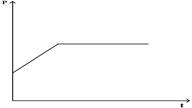 Зависимость импульса от времени для прямолинейно движущегося тела представлена на графике.
Зависимость импульса от времени для прямолинейно движущегося тела представлена на графике.
Зависимость равнодействующей силы от времени имеет вид
R 
£ 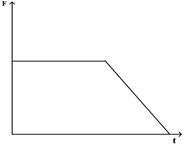
£ 
56. Задание {{ 74 }} ТЗ № 74
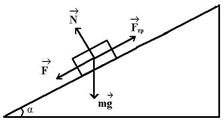
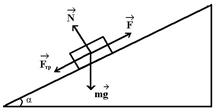 Уравнение движения тела по наклонной плоскости имеет вид
Уравнение движения тела по наклонной плоскости имеет вид 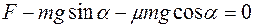 . Данное тело движется по плоскости
. Данное тело движется по плоскости
£ равномерно вниз
R равномерно вверх
£ равноускоренно вниз
£ равноускоренно вверх
57. Задание {{ 75 }} ТЗ № 75
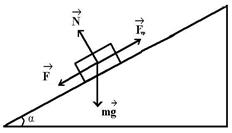 Уравнение движения тела по наклонной
Уравнение движения тела по наклонной
плоскости имеет вид 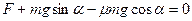 .
.
Данное тело движется по плоскости
R равномерно вниз
£ равномерно вверх
£ равноускоренно вниз
£ равноускоренно вверх
58. Задание {{ 76 }} ТЗ № 76
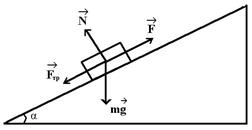 Уравнение движения тела по наклонной плоскости имеет вид
Уравнение движения тела по наклонной плоскости имеет вид 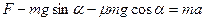 .
.
Данное тело движется по плоскости
£ равномерно вниз
£  Уравнение движения тела по наклонной плоскости
Уравнение движения тела по наклонной плоскости
имеет вид 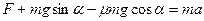 .
.
Данное тело движется по плоскости
£ равномерно вниз
£ равноускоренно вниз
£ равноускоренно вверх
60. Задание {{ 43 }} ТЗ № 43
Сила тяжести имеет вид
£ 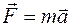
R 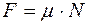
£ 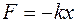
61. Задание {{ 44 }} ТЗ № 44
Сила трения скольжения имеет вид
£ 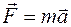
£ 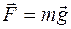
R 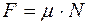
£ 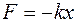
62. Задание {{ 45 }} ТЗ № 45
Сила упругости имеет вид
£ 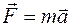
£ 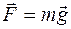
£ 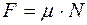
R 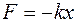
63. Задание {{ 46 }} ТЗ № 46

£ Второй закон Ньютона имеет вид
£ 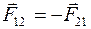
£ 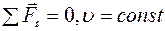
R 
65. Задание {{ 48 }} ТЗ № 48
Третий закон Ньютона имеет вид
£ 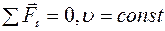
£ 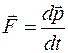
£ 
R 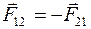
66. Задание {{ 49 }} ТЗ № 49
Импульс материальной точки имеет вид
R 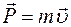
£ 
£ 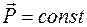
£ 
67. Задание {{ 50 }} ТЗ № 50
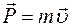
R 
£ 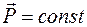
£ 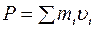
68. Задание {{ 51 }} ТЗ № 51
Закон сохранения импульса системы имеет вид
£ 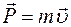
£ 
R 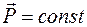
£ 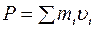
69. Задание {{ 52 }} ТЗ № 52
В ИСО сила 50 н сообщает телу массой 10 кг ускорение [м/ 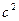 ]
]
R 5
£ 40
£ 60
£ 500
70. Задание {{ 53 }} ТЗ № 53
В ИСО сила 50 н сообщает телу массой 5 кг некоторое ускорение. Масса тела, которому сила в 60 н сообщает такое же ускорение, равна [кг]
£ 4
£ 5
R 6
£ 10
71. Задание {{ 54 }} ТЗ № 54
В ИСО сила 20 н сообщает телу ускорение 5 м/ 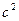 . Сила в 10 н сообщает этому же телу ускорение равное [м/
. Сила в 10 н сообщает этому же телу ускорение равное [м/ 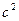 ]
]
£ 2
R 2,5
£ 4
£ 4,5
72. Задание {{ 55 }} ТЗ № 55
увеличится в 4 раза
£ увеличится в 16 раз
£ уменьшится в 4 раза
£ уменьшится в 16 раз
73. Задание {{ 56 }} ТЗ № 56
Под действием силы в 20 н пружина жесткостью 500н/м растянется на [см]
£ 5
£ 10
£ 25
R 4
74. Задание {{ 57 }} ТЗ № 57
Сани с грузом имеют общую массу 500 кг и скользят по горизонтальной дороге. Чтобы уменьшить трение на 20% , надо снять груз массой [кг]
£ 50
R 100
£ 150
£ 200
75. Задание {{ 58 }} ТЗ № 58
Груз массой 2 кг висит на пружине жесткостью 500н/м. Если груз равномерно поднимать вверх, то пружина растянется на [cм]
£ 2
R 4
£ 8
£ 10
76. Задание {{ 59 }} ТЗ № 59
Груз массой 2 кг висит на пружине жесткость, которой 500 н/м. Если груз поднимать с ускорением 2 м/ 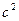 , то пружина растянется на [мм]
, то пружина растянется на [мм]
£ 40
£ 45
R 48
£ 50
77. Задание {{ 60 }} ТЗ № 60
Груз массой 2 кг висит на пружине жесткость, которой 500 н/м. Если груз опускать с ускорением 2 м/ 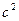 , то пружина растянется на [мм]
, то пружина растянется на [мм]
£ 42
£ 40
R 32
£ 30
Дата: 2019-04-23, просмотров: 359.