|
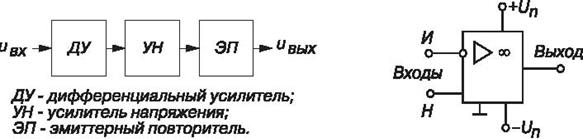
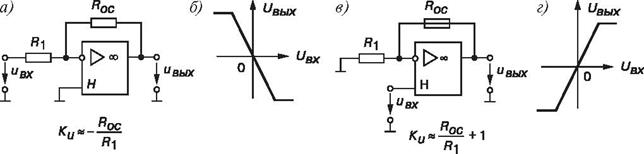
Операционный усилитель имеет два входа: инвертирующий (И) и неинвертирующий (Н). Их название связано с тем, что в первом случае выходное напряжение находится в противофазе с входным, а во втором случае — в фазе с входным напряжением. Для питания ОУ обычно используют два разнополярных источника питания +Un и -Un или один биполярный источник, средняя точка трансформатора которого соединена с общей шиной, относительно которой измеряются напряжения +Un и -Un, равные (±6,3)...(±15) B . Для получения нужных свойств к дополнительным выводам ОУ подключают звенья обратной связи. Подключив звено отрицательной обратной связи (ООС), состоящее из двух резисторов (делителя), например, Roc ≈ 1 МОм и R1 ≈ 5 кОм, между выходом и инвертирующим входом, и соединив вход Н с общей точкой, получим инвертирующий усилитель , статическая амплитудная характеристика которого UВЫХ =f (UВX ) б. Максимальное значение напряжения UВых.max =−Ku (UВX1 −UВX2) ≈ (0,8...0,9)Un , т. е. на 1...3 В меньше напряжения питания Un.
|
Схема неинвертирующего усилителя и его амплитудная характеристика Uвых(Uвх) изображены на рис. в, г. Коэффициент усиления инвертирующего ОУ c ООС Ku.ос приближенно определяется отношением сопротивлений резисторов Roc и R1 звена ООС и не зависит от коэффициента усиления самого ОУ (Ku = 105….106). Без обратных связей ОУ не применяется изза его практически бесконечного значения коэффициента Ku (для идеального ОУ Ku = ∞; Rвх = ∞; Rвых = 0). Основными параметрами ОУ наряду с коэффициентом Кu являются:
· входное сопротивление Rвх ≈104…107 Ом;
· выходное сопротивление Rвых ≈ 102 Ом;
· входное напряжение смещения нуля Uсм (единицы милливольт);
· частота единичного усиления f1 (единицы и десятки мегагерц), т. е. частота, при которой Ku = 1;
· скорость нарастания выходного напряжения (v ≈ 0,1…100 В/мкс) от Uвых = = 0 до U вых = Uвых.max;
· время установления выходного напряжения (tуст = 0,05…2 мкс) от Uвых = 0 до Uвых = U вых.max.
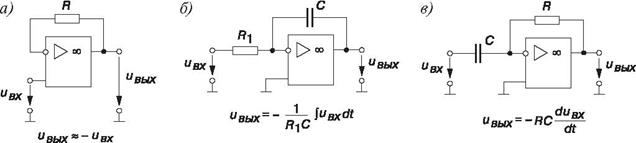
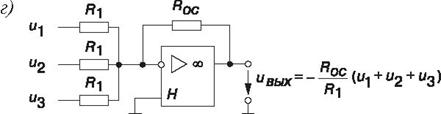
На основе ОУ строят функциональные узлы для выполнения различных математических операций: повторитель (а), интегратор (б), дифференциатор (в), сумматор (г) и др. Кроме этого, операционные усилители часто используют при конструировании компараторов, генераторов гармонических колебаний и сигналов различной формы, избирательных усилителей, аналогоцифровых и цифроаналоговых преобразователей и других устройств.
|
|
Цифровая техника
Основные термины и понятия.
Цифровыми называют устройства, предназначенные для формирования, преобразования и передачи кодовых слов. При этом кодовые слова (коды или числа) в электронных цифровых устройствах представляются в виде последовательностей электрических импульсов (сигналов с двумя уровнями напряжения: высоким и низким), а их преобразования осуществляются арифметическими, логическими, запоминающими и вспомогательными устройствами.
Элементами и узлами цифровых устройств, служащими основой для построения микропроцессоров, микропроцессорных систем, компьютеров, автоматизированных систем управления объектами, технологическими процессами и информационными потоками являются: дешифраторы, сумматоры, триггеры, регистры, счетчики и многие другие.
В современных устройствах цифровой обработки информации используется два класса переменных: числа и логические переменные. Числа несут информацию о количественных характеристиках процесса, объекта, системы, над ними можно производить арифметические действия. Логические переменные определяют состояние системы или принадлежность её к определенному классу состояний.
Главная особенность цифровых устройств (по отношению к аналоговым и импульсным устройствам) состоит в том, что объектами информации являются двоичные числа (кодовые слова) и логические переменные, а не функции времени.
Числа и логические переменные связаны друг с другом при решении задач управления и обработки информации. В вычислительных задачах вначале определяются совокупность и значения входных воздействий на объект управления. Предполагается, что существует математическая модель объекта в виде набора формул, таблиц, графиков и несколько логических условий. При решении задач необходимо вести анализ логических условий с выдачей логических команд. Для решения таких задач необходим специальный математический аппарат и соответствующие устройства.
Устройство в ЭВМ, выполняющее арифметические и логические операции называют арифметико-логическим устройством (АЛУ), а АЛУ, выполняющее также функции управления — центральным процессором.
Арифметические устройства (сумматоры, умножители) предназначены для выполнения арифметических операций над бинарными кодовыми словами. Числа (кодовые слова) в цифровых устройствах обычно представляют в позиционной двоичной системе счисления, осуществляемой по следующему правилу:
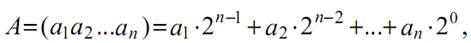
где а1, а2, ., ап — весовые коэффициенты, принимающие значения 1 и 0; п — число разрядов в коде. Например, 26(10) = 11010(2), п = 5.
Код, построенный по этому принципу, принято относить к арифметическим кодам, на которые распространяются арифметические операции сложения, вычитания, умножения и деления.
Число символов в кодовом слове цифрового устройства обычно фиксировано, т. е. кодовые слова имеют одинаковую длину. Если кодовое слово имеет п символов (разрядов), то из них можно составить N = 2n комбинаций кодовых слов. Например, в 32 разрядном вычислительном устройстве можно закодировать 232 = 4 296 967 298 слов.
Для оценки количества цифровой информации используют бит и байт (1 байт = 8 бит). 1 бит — это мера информации, выражающая такое её количество, которое может передать один символ двоичного алфавита при равной вероятности появления каждого символа алфавита:
Так, в 8разрядном слове информационная ёмкость равна 8 битам или 1 байту.
С информационной точки зрения функции арифметического цифрового устройства состоят в преобразовании входного п-разрядного двоичного числа в m-разрядное выходное двоичное слово (число).
В цифровых вычислительных системах наряду с двоичной широко используют также восьмеричную (для кодирования адресов и команд), шестнадцатеричную (цифробуквенную), десятичнодвоичную и другие системы счисления .
Логическими устройствами называют схемные элементы, с помощью которых осуществляется преобразование поступающих на их входы двоичных (бинарных) сигналов и непосредственное выполнение предусмотренных логических операций.
Запоминающими называют такие устройства, которые обладают свойствами длительно сохранять поступающую в них информацию без изменения её содержания и отправлять её по команде в другие устройства.
Вспомогательными являются все прочие устройства, предназначенные для образования надёжных связей между арифметикологическими и запоминающими функциональными узлами и внешними устройствами. К ним относят тактовые генераторы, устройства приёма и распределения данных, таймеры, усилители, повторители, инверторы и др. Функционирование цифровых устройств можно представить следующим образом:
- посредством генератора тактовых импульсов производится синхронизация начала выполнения отдельных операций преобразования входного кодового слова и отводится время выполнения команды (в течение одного или нескольких периодов тактовых импульсов);
- после активизации начала операции осуществляется преобразование всех входных кодовых слов (логических нулей и единиц) в требуемые выходные кодовые слова;
- выходные кодовые слова отправляются на хранение в память цифрового устройства и/или во внешние устройства для выполнения определенных действий.
Операции над кодовыми словами, представленными в виде электрических сигналов, в цифровом устройстве могут выполняться следующими двумя способами:
- последовательное (поразрядное, побитовое) выполнение операций, при котором символы 1 и 0 кодового слова поступают последовательно по времени на единственный вход цифрового устройства и по завершении операции последовательно символ за символом выводятся из него.
- параллельное выполнение операций, при котором символы 1 и 0 кодового слова поступают одновременно на три входа ЦУ и по завершении операции одновременно выводятся из него .
Элементы булевой алгебры
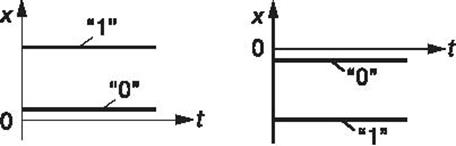
Работа любого логического устройства подчиняется законам формальной логики, которые не допускают уклончивых ответов. Решение логических задач осуществляется с помощью логических элементов, базирующихся на математическом аппарате алгебры логики (булевой алгебры, разработанной английским математиком Джорджем Булем (1815–1864)), в которой все переменные величины (аргументы хi и функции уi) могут принимать только два логических значения: "1" (логическая единица) и "0" (логический ноль). Во многих случаях эти символы простейшего алфавита, состоящего из двух букв, отождествляют с арабскими цифрами 1 и 0, не вкладывая в них смысла количества.
Понятия "1" и "0" являются условными, символизирующими состояния, например, релейного устройства: "включено", "выключено". Как отмечалось, в цифровых электронных устройствах применяют сигналы двух уровней напряжения: положительную потенциальную логику
|
| |
| а) | б) |
в которой символ "1" кодируется высоким потенциалом, а "0" — низким, и отрицательную (рис. б), в которой символ "1" кодируется отрицательным потенциалом, а "0" — близким к нулевому. В данной теме будем использовать способ кодирования, называемый соглашением положительной логики.
В общем случае логическое устройство может иметь п входов и m выходов. Рассматривая входные сигналы х1, х2, ., хп в качестве аргументов, можно соответствующие выходные сигналы представлять в виде функции уi = f(х0, х1, х2, ., хп) с помощью операций алгебры логики.
Функции алгебры логики (ФАЛ), иногда называемые переключательными функциями, представляют в нескольких формах:
- в алгебраической (в виде математического выражения): yi = (x0 / x1) V (x1 / x2);
- в виде таблиц истинности или комбинационных таблиц.
В булевой алгебре выделяют три основные функции: конъюнкция, дизъюнкция, отрицание. Остальные функции являются производными от приведенных выше. Основные логические операции состоят из следующих элементарных преобразований двоичных сигналов:
Логические операции преобразуют по определенным правилам входную информацию, обозначаемую символами Х1, Х2, Х3, ..., Хn, в выходную, которую обозначим буквой F. Условные обозначения основных логических элементов показаны на рисунке 4.45, таблица истинности приведена в таблице 4.3 для двух значений входных сигналов — Х1 и Х2.
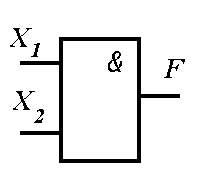
| 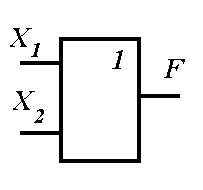
| 
|
| а) | б) | в) |
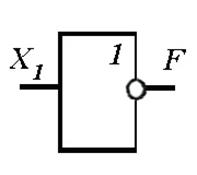
Графические обозначения основных логических элементов (операций):
а — элемент «И», б — элемент «ИЛИ», в — элемент «НЕ»
Рассмотрим основные логические операции.
1. Логическое умножение (конъюнкция), или операция «И», обозначается в формулах булевой алгебры знаками «*» или «^». Символически операция записывается выражениями:
F = Х 1 * Х 2 * Х 3 * … * Хn или F = Х1 ^ Х2 ^ Х3 ^… ^ Хn.
Логика срабатывания этой операции состоит в том, что на выходе ЛЭ будет сигнал «1» только в том случае, если на и X1 ,и Х2,и Х3, и т.д.входы поступят, т.е. если на входах будут все сигналы, предусмотренные в данной операции (все true), то и на выходе будет сигнал (truе). При этом ложное высказывание будет истинным, если истинны все простые высказывания.
2. Логическое сложение (дизъюнкция), она же операция «ИЛИ», обозначается знаками «+», « 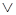 ». Символически операция записывается следующими выражениями:
». Символически операция записывается следующими выражениями:
F = Х1 + Х2 + Х3 + … + Хn; F = Х1 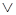 Х2
Х2 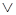 Х3
Х3 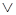 …
… 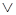 Хn.
Хn.
Логика срабатывания этой операции состоит в том, что на выходе ЛЭ «ИЛИ» будет сигнал «1» в том случае, если на его входы или Х1, или Х2, или Х3 и т.д. поступит хотя бы один сигнал «1» из всех предусмотренных. Другими словами, сложное высказывание будет истинным (truе), если истинно хотя бы одно из простых высказываний, и ложным (false), если ложны (false) все простые высказывания.
3. Логическое отрицание (инверсия), или «НЕ», обозначается чертой над входной (входными) переменной. Символически записывается:
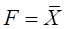
На схемах условное обозначение этой логической операции — кружочек на выходе прямоугольника (рисунок 4.45, в). Смысл этой операции состоит в том, что на выходе этого ЛЭ сигнал будет лишь в том случае, если на входе сигнала нет. Если на входе есть сигнал, то на выходе он отсутствует. Это простое отрицание, которое используется сравнительно редко.
Гораздо чаще используется операция «НЕ» в сочетании с операциями «И» или «ИЛИ». Рассмотрим такие составные операции.
4. Отрицание логического умножения, или операция «И-НЕ». . Символически операция записывается выражениями:
_____________ ______________
F=Х 1 *Х 2 *Х 3 *...*Хn или F=Х1^Х2^Х3^...^Хn .
Логика срабатывания операции «И-НЕ» заключается в том, что сигнал на выходе этого ЛЭ будет в том случае, если отсутствует сигнал хотя бы на одном входе. Эта операция известна также под названием «штрих Шеффера», образует сложное высказывание из простых по следующему правилу: сложное высказывание истинно, если ложно хотя бы одно из простых высказываний, и ложно, если все простые высказывания истинны
На входы ЛЭ при любой логической операции подается вполне определенное количество входных сигналов, поэтому и в символике записи это находит отражение. Например, если на входы подаются два сигнала, то получим «2И-НЕ», если три сигнала, то «3И-НЕ», или символьно:
_____ ________
F = Х1*Х2, F=Х1*Х2*Х3 соответственно и так далее.
5. Отрицание логического сложения, или операция «ИЛИ-НЕ». Символически операция записывается выражениями:
_____________ ______________
F=Х 1 +Х2+Х3+...+Хn или F=Х1VХ2VХ3V... VХn
Смысл этой операции состоит в том, что на выходе этого устройства сигнал будет лишь в том случае, если нет сигналов на его входах. Если появится сигнал хотя бы на одном входе ЛЭ, реализующего операцию «ИЛИ-НЕ», то на выходе сигнала не будет. Операция «ИЛИ-НЕ» называется также «стрелкой Пирса», образует сложное высказывание из простых в соответствии со следующим правилом: сложное высказывание истинно лишь в том случае, когда ложны все образующие его простые высказывания, и ложно, если истинно хотя бы одно из простых высказываний.
На входы ЛЭ при любой логической операции подается вполне определенное количество входных сигналов, поэтому и в символике записи это находит отражение. Например, если на входы подаются два сигнала, то получим: «2ИЛИ-НЕ», если три сигнала, то «3ИЛИ-НЕ», или символьно:
_____ ________
F = Х1+Х2, F=Х1+Х2+Х3 соответственно и так далее.
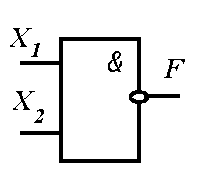
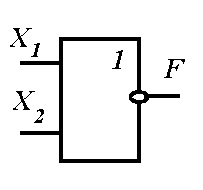
| 
|
| а) | б) |
Графические обозначения составных логических элементов (операций): а — элемент «И-НЕ»; б — элемент «ИЛИ-НЕ»
Таблица логических операций
| X 1 | X 2 | F | |||
| «И» | «ИЛИ» | «2И-НЕ» | «2ИЛИ-НЕ» | ||
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 |
Комбинационные устройства.
В общем случае на вход цифрового устройства поступает n (n ≥ 1) двоичных переменных Х (х1х2...хп), а с выхода снимается m (m ≥1) двоичных переменных F (F1,F2….F m). При этом устройства осуществляют (реализуют) определенную связь (ФАЛ) между входными и выходными переменными.
По способу функционирования цифровые устройства делят на комбинационные и последовательностные.
В комбинационных устройствах (автоматах без памяти) значения F в течение каждого такта работы определяются значениями Х только в этот же такт, и не зависят от того, какие переменные подавались на входы в предыдущие такты, т. е. F = f(Х). Другими словами, эти устройства, состоящие только из логических элементов, лишены памяти: не хранят информацию о прошлом. Входные и выходные сигналы комбинационных устройств могут принимать только два значения: 1 и 0.
В качестве примера можно привести работу логического элемента И-НЕ с двумя входами и одним выходом.
В теоретических рассмотрениях (как и в данной теме) обычно считается, что сигналы на выходе комбинационного устройства (КУ) появляются в тот же момент, когда на вход устройства поступают инициирующие их входные сигналы, т. е. предполагается их быстродействие бесконечным.
В реальных электронных приборах задержка выходного сигнала τ > 0 (τ = 10-9… 10-10 с — естественный физический предел электронных приборов, а в сложных устройствах с последовательным соединением логических элементов задержки суммируются.
Комбинационные узлы и блоки цифровых устройств либо собирают из отдельных микросхем малой степени интеграции (элементов И-НЕ, ИЛИ-НЕ и др.), либо изготавливают в виде систем средней интеграции, либо входят в состав БИС и СБИС. Различные типы комбинационных узлов и блоков широко используются в устройствах ввода-вывода и управления, в операционных запоминающих устройствах современных цифровых систем.
По функциональному назначению можно выделить следующие классы КУ: сумматоры, шифраторы и дешифраторы, цифровые компараторы, мультиплексоры и демультиплексоры, преобразователи кодов, программируемые логические матрицы, перемножители, арифметикологические устройства.
Для построения цифровых систем, кроме комбинационных узлов, требуются последовательностные устройства (автоматы с памятью), значения выходных двоичных переменных F которых определяются как значениями входных переменных Х в течение рассматриваемого такта работы, так и существовавшими переменными в ряде предыдущих тактов. Для этого в последовательностных устройствах, кроме логических, должны быть еще и запоминающие элементы — элементы памяти (ЭП) с множеством входов и выходов, называемые также цепями обратной связи. При этом память устройства может охватывать не бесконечно большое, а лишь конечное число тактов, формируемых генератором тактовых импульсов (ГТИ) Поэтому цифровые устройства с памятью называют конечными автоматами, которыми являются все ЭВМ.
Подобно входным переменным Х и выходным F, переменные, сохраняемые в памяти устройства, тоже двоичные и зависят от значений входных переменных в предыдущих тактах.
Дешифраторы.
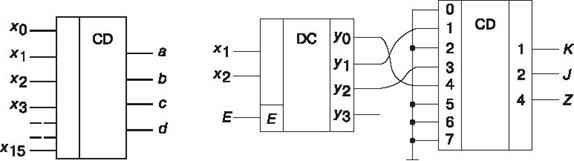
Дешифратор или декодер — комбинационная схема с п входами и m выходами (m > n), преобразующая двоичный входной п-код (кодовое слово) в унитарный. На одном из m выходов дешифратора появляется логическая единица, а именно на том, номер которого равен поданному на вход двоичному числу. На всех остальных выходах дешифратора выходные сигналы равны нулю. Дешифратор используют, когда нужно обращаться к различным цифровым устройствам, и при этом номер устройства — его адрес — представлен двоичным кодом.
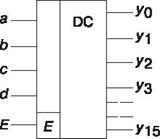
| Условное изображение дешифратора 4-16 (читаемого "четыре в шестнадцать") на схемах представлено на рисунке. Дешифратор DC содержит число выходов, равное числу комбинаций входных переменных, например, при п = 4, m = 2п = 16, от у0= abcd до y15 = abcd. Применяются также неполные дешифраторы с меньшим числом выводов (10 или 12 при четырех переменных на входе, |
тогда ряд комбинаций на входе не используется). Каждый выход полного дешифратора реализует конъюнкцию входных переменных (код адреса) или их инверсий: при наборе abcd (0000), у0 = 1; при a bcd (0111), у7 = 1; при abcd (1111), y15 = 1 и т. д.
Дешифраторы часто имеют разрешающий (управляющий, стробирующий) вход Е. При Е = 1 дешифратор функционирует как обычно, при Е = 0 на всех выводах устанавливается 0 независимо от поступающего кода адреса. Дешифраторы широко используют во многих устройствах, в том числе в качестве преобразователей двоичного кода в десятичный.
Шифратор (CD) или кодер выполняет функцию, обратную дешифратору. Условное изображение шифратора 16-4 на схемах показано на рис. 4.48, а. Классический шифратор имеет n входов и m выходов (m < n), и при подаче сигнала на один из входов (и не более) на выходе узла появляется двоичный код номера возбуждённого выхода. Число входов и выходов такого шифратора связано соотношением n = 2m .
|
| |
| а) | б) |
Области использования шифраторов — отображение в виде двоичного кода номера нажатой кнопки или положения многопозиционного переключателя, а также номера устройства, подавшего сигнал на обслуживание в микропроцессорных системах, входят в состав микросхем контроллеров прерываний, например, КР580ВН59.
Для решения многих конкретных задач необходимо синтезировать преобразователи произвольных кодов.
Эффективно стыкуются друг с другом декодер и кодер, построенные на элементах ИНЕ: первый имеет инверсные выходы, а второй — инверсные входы. Если некоторым входным комбинациям соответствует одна и та же выходная, то соответствующие выходы декодера объединяют на элементе ИЛИ и выход последнего подают на нужный вход кодера.
Проектирование кодовой преобразовательной схемы на паре декодер-кодер оказывается в среднем более выгодным и по числу корпусов, и по быстродействию, чем при проектировании из готовых базовых логических микросхем И-НЕ и ИЛИ-НЕ . Однако потребляемая мощность в этом случае может оказаться больше, чем у схемы из отдельных элементов. Затраты времени инженера на логическое проектирование по схеме декодеркодер неизмеримо меньше, чем затраты на проектирование преобразователя из россыпи.
Компаратор.
Цифровой компаратор предназначен для определения равенства двоичных чисел. Операция поразрядного сравнения заключается в выработке признака равенства (равнозначности) или неравенства (неравнозначности) двух сравниваемых двоичных чисел. Два числа равны при равенстве цифр в одноименных разрядах: аi = bi, где аi — цифра в i-ом разряде одного числа; bi — цифра в i-ом разряде другого числа. Равенство аi = bi имеет место при аi = 1, bi = 1 или при аi = 0, bi = 0. Поэтому логическая функция, выражающая это равенство, равна единице, если единице равно произведение этих цифр или произведение их инверсных значений, т. е.
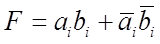 ,
,
а логическая функция, описывающая компаратор, имеет вид
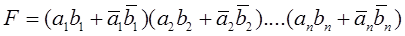
Для построения компаратора только на элементах И-НЕ, запишем её в другой форме, воспользовавшись формулами де Моргана,
F 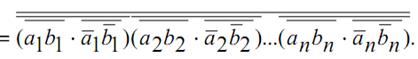
Схема, реализующая это выражение
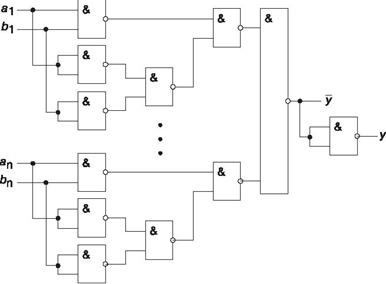
Сумматор.
Сумматор — это узел, в котором выполняется арифметическая операция суммирования цифровых кодов двух двоичных чисел. Известно, что числа в любой позиционной системе счисления складываются поразрядно. Поэтому для сложения двух чисел нужно иметь типовые узлы, реализующие суммирование цифр одного разряда слагаемых с учетом возможного переноса единицы из соседнего младшего разряда. К таким узлам относят одноразрядные комбинационные полусумматоры и сумматоры.
При построении сумматоров на интегральных микросхемах для обеспечения быстродействия и минимального количества однотипных логических элементов необходимо уменьшить число последовательно включенных элементов. Анализ показал, что более экономичной по количеству элементов и быстродействующей является функциональная схема полусумматора, реализующая переключательную функцию: На практике наибольшее распространение получили двоичнокодированные десятичные сумматоры.
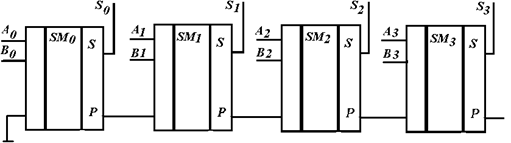
На входы а0, а1, а2, а3 подается двоичный код одной из суммируемых десятичных цифр, на входы b0, b1, b2, b3 — двоичный код второй десятичной цифры, а на вход рi — значение переноса из соседнего младшего разряда. На выходах S0, S1, S2, S3 образуется двоичный код десятичной цифры данного разряда суммы, а на выходе pi+1 — значение переноса в соседний старший разряд.
Для выполнения действий над десятичными цифрами, представленными тетрадами, наиболее широко используют код с избытком 6. При выполнении логических операций в этот код преобразуются числа, хранящиеся в оперативной памяти в коде 8421. Операция вычитания обычно заменяется сложением в дополнительных кодах, т. е. к первоначальной сумме прибавляется код 01102.
Триггеры.
Как отмечалось, состояние конечного автомата предполагает наличие у него внутренней памяти. Число различных состояний автомата зависит от глубины этой памяти. В качестве элементов памяти могут использоваться стандартные модули ПЗУ или логические схемы с обратными связями, в частности, триггеры.
Триггер — устройство, обладающее двумя устойчивыми состояниями и способное переходить из одного состояния в другое под воздействием внешнего управляющего сигнала, превышающего пороговое значение. При отсутствии внешних воздействий триггер может сколь угодно долго находиться в одном из устойчивых состояний. Триггеры могут выполнять функции реле, переключателей, на их основе строят счетчики, распределители и другие устройства.
Различают триггеры асинхронные, которые переключаются в момент подачи входного сигнала, и синхронные (тактируемые), которые переключаются только при подаче синхронизирующих импульсов, а момент перехода связан с определенным уровнем синхросигнала (статические триггеры) или с моментом фронта либо среза синхросигнала (динамические триггеры).
RS-триггер
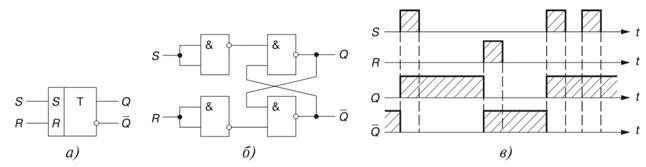
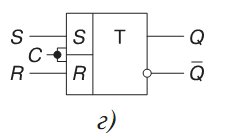
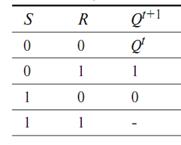
Простейшим триггером является RS-триггер, принцип его действия поясняется таблицей истинности. Триггер имеет два раздельных входа — R (установки нуля на выходе, Q = 0) и S (установки 1 на выходе, Q = 1) и два выхода — прямой Q и инверсный Q . Независимым является один выход Q, так как сигнал Q можно получить с помощью внешнего инвертора.
|
| |
| 
|
|
| |
Рассмотрим таблицу истинности. До поступления сигнала на Sвход сигнал на выходе триггера обозначен Qt. При подаче сигнала 1 на Sвход (S = 1, команда "включить") триггер переходит в состояние Qt+1 = 1. При поступлении сигнала 1 на Rвход (R = 1, команда "выключить") устанавливается Qt+1 = 0. При отсутствии новых команд состояние триггера не изменяется: триггер сохраняет информацию о последней из поступивших команд. Естественно, что команда "включить — выключить" (S = R = 1) является недопустимой: при таком сочетании входных переменных в RS- триггере возникает неопределенность, и это сочетание не используется.
В момент, когда устанавливается S = 1, триггер переходит в состояние Q = 1. При отсутствии входных сигналов состояние триггера не изменяется, а в момент установления R = 1 триггер переключается в состояние Q = 0, в котором пребывает до поступления нового единичного сигнала на Sвход.
RS- триггер может быть построен на различных логических элементах. Показана схема реализации RS- триггера на логических элементах ИНЕ, в которой использована обратная связь (ОС) с выходов триггера на входы логических элементов. Именно наличие ОС отличает триггеры от ранее рассмотренных комбинационных устройств: сигнал ОС позволяет в триггере учитывать его предшествующее состояние.
D-Триггер
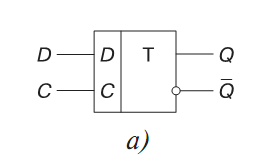
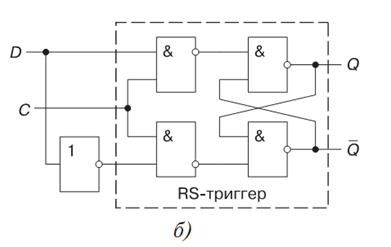
Триггер задержки (D-триггер) имеет один информационный D-вход и тактовый С вход. Реализовать его можно на различных логических элементах, в том числе на основе синхронного RS- триггера, дополненного инвертором.
| 
|
| 
|
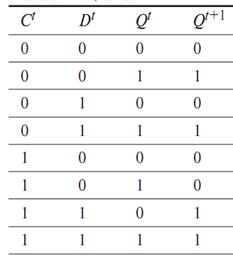
Синхронный D-триггер функционирует в соответствии с таблицей истинности, из которой видно, что при отсутствии синхроимпульса (С = 0) состояние триггера остается неизменным. При условии же С = 1 триггер передает на выход сигнал, поступивший на его вход D в предыдущем такте.
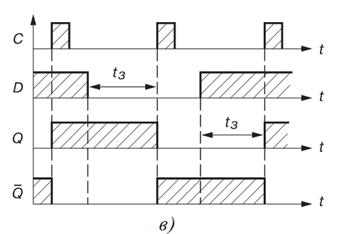
Приведены временные диаграммы D-триггера. Выход Q повторяет состояние D-входа с поступлением очередного тактового импульса на вход С с задержкой tз относительно сменившегося логического состояния на Dвходе.
JK-триггеры
JK-триггеры обычно выполняют тактируемыми. Такой JK-триггер имеет информационные входы J и K, которые по своему воздействию на устройство аналогичны входам S и R тактируемого RS-триггера: при J = 1, K = 0 триггер по тактовому импульсу С устанавливается в состояние Q = 1; при J = 0, K = 1 — переключается в состояние Q = 0, а при J = K = 0 — хранит ранее принятую информацию.
В отличие от тактируемого RS-триггера одновременное присутствие логических 1 на информационных входах не является для JK-триггера запрещенной комбинацией; при J = K = 1 триггер работает в счетном режиме, т. е. переключается каждым тактовым импульсом на входе С.
На рисунке изображена одна из функциональных схем JK-триггера. При J = K = 0 на выходе элементов Э1 и Э2 устанавливаются логические 1, которые для триггеров с инверсными входами являются пассивными сигналами: триггер Т1 и, следовательно, JK-триггер в целом сохраняют прежнее состояние.
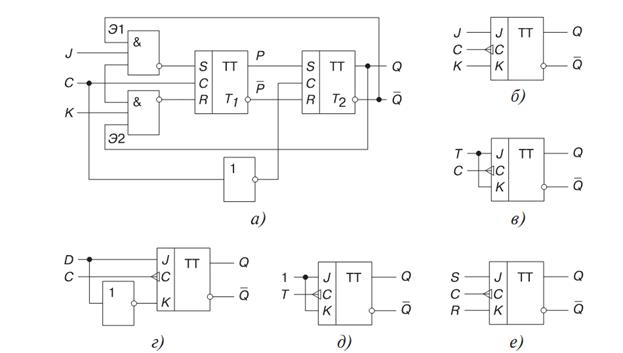
Логическая 1 на одном из входов элемента И-НЕ не определяет 1 на его выходе, и сочетание J = K = 1 никак не влияет на входную логику первой ступени, поэтому JK-триггер работает в счетном режиме. Только при наличии сигналов J = 1, С = 1 и Q = 1 на входе элемента Э1 триггер Т1 переключится в состояние Р = 1. Аналогично логический 0 будет на выходе элемента Э2, когда К = 1, С = 1 и Q = 1.
Таким образом, комбинация J = 1, К = 0 обуславливает по тактовому импульсу С = 1 переключение JK-триггера в целом в состояние Q = 1, а комбинация J = 0, К = 1 — в состояние Q = 0.
Состояние триггера определяется не только уровнями сигналов на информационных входах J и К, но и состоянием Qt, в котором ранее находился JK-триггер.
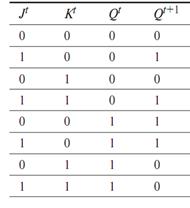
При проектировании сложных логических схем необходимы триггеры различных типов. Поэтому выгоднее изготовить универсальный тип триггера, который можно использовать в разных режимах работы и модификациях. В интегральной схемотехнике наибольшее распространение получили синхронные D и JK-триггеры.
Счетчики.
Счётчик предназначен для счёта поступающих на его вход импульсов, в интервале между которыми он должен хранить информацию об их количестве. Поэтому счётчик состоит из запоминающих ячеек — триггеров обычно D или JKтипа. Между собой ячейки счётчика соединяют таким образом, чтобы каждому числу импульсов соответствовали состояния 1 или 0 определенных ячеек. При этом совокупность единиц и нулей на выходах п ячеек, называемых разрядами счетчика, представляет собой п-разрядное двоичное число, которое однозначно определяет количество прошедших через входы импульсов.
Каждый разряд счётчика может находиться в двух состояниях. Число устойчивых состояний, которое может принимать данный счётчик, называют коэффициентом пересчёта Kсч.
Если с каждым входным импульсом "записанное" в счётчике число увеличивается, то такой счётчик является суммирующим, если же оно уменьшается, то — вычитающим. Счётчик, работающий как на сложение, так и на вычитание, называют реверсивным.
Счётчики, у которых под воздействием входного импульса переключение соответствующих разрядов происходит последовательно друг за другом, называют асинхронными, а когда переключение происходит одновременно — синхронными. Максимальное число N, которое может быть записано в счётчике, равно (2п — 1), где п — число разрядов счётчика.
По способу кодирования последовательных состояний различают двоичные счетчики с коэффициентами пересчёта (обнуления) Kсч = 2п, у которых порядок смены состояний триггеров соответствует последовательности двоичных чисел, и недвоичные, у которых Kсч < 2п (например, десятичные с коэффициентом Kсч = 10 или делители частоты с коэффициентом деления Kсч≠2п).
Счётчики входят в состав разнообразных цифровых устройств: электронных часов, делителей частоты, распределителей импульсов, вычислительных и управляющих устройств. Выпускаемые промышленностью интегральные счётчики представляют собой схемы средней интеграции (например, микросхемы серий К155, К176 и др.); среди них многоразрядные бинарные счётчики на сложение и реверсивные счётчики с установочными входами R и S для всех разрядов, с постоянными и произвольными коэффициентами пересчёта.
ЛИТЕРАТУРА.
1. Касаткин, А.С. Электротехника / А.С. Касаткин, М.В. Немцов. — Москва: Энергоатомиздат, 1983.— 427 с.
2. Кiтуновiч, Ф.Г. Электратэхнiка / Ф.Г. Кiтуновiч. — Мiнск: Вышэйшая школа, 1998. — 429 с.
3. Электротехника / Б.А. Волынский, В.Н. Зейн, В.Е. Шатерников. — Москва: Энергоатомиздат, 1987.
4. Асинхронные машины / под ред. И.П. Копылова. — Москва: Высшая школа, 1977. 328 с.
5. Осин, И.Л. Электрические машины. Синхронные машины / И.Л. Осин, Ю.Г. Шакарян; под ред. И.П. Копылова. — Москва: Высшая школа, 1990. 304 с.
6. Хвостов, В.С. Электрические машины. Машины постоянного тока / В.С. Хвостов; под ред. И.П. Копылова. — Москва: Высшая школа, 1989. — 335 с.
7. Морозов, А.Г. Электротехника, электроника и импульсная техника / А.Г. Морозов. — Москва: Высшая школа, 1987.
8. Галкин, В.И. Промышленная электроника / В.И. Галкин. — Минск: Вышэйшая школа, 1989.
9. Лабораторные работы (практикум) по курсу «Электротехника и электроника» для студентов неэлектрических специальностей: Ч. 3. Электроника / Розум Т.Т. [и др.]. — Минск: БГПА, 1988.
10. Игумнов Д. В., Костюнина Г. П. Основы полупроводниковой электроники. Учебное пособие. — М.: Горячая линия — Телеком, 2005, 392 с.
11. Тотхейм Р. Основы цифровой электроники. — М.: Мир, 1988, 392 с.
12. Электротехника и электроника. Учебник для вузов. Книга 3. Электрические измерения и основы электроники. / Под ред. проф. В. Г. Герасимова. — М.: Энергоатомиздат, 1998, 432 с.
13. ГОСТ 2552982. Диоды полупроводниковые. Термины, определения и буквенные обозначения параметров.
14. ГОСТ 2033284. Тиристоры. Термины, определения и буквенные обозначения параметров.
15. ГОСТ 2000374. Транзисторы биполярные. Термины, определения и буквенные обозначения параметров.
16. ГОСТ 1909573. Транзисторы полевые. Термины, определения и буквенные обозначения параметров.
17. ГОСТ 1948089. Микросхемы интегральные. Термины, определения и буквенные обозначения электрических параметров.
Дата: 2019-04-23, просмотров: 477.