Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Цель работы: познакомиться с основными методами обнаружения и устранения систематических и случайных погрешностей.

Приборы и оборудование: рычажные весы, разновесы, стакан с речным песком, груз, наборы тел одинакового размера (10шт.), штангенциркуль.

Теоретические сведения

Погрешность средства измерения – разность между показаниями средства измерения и истинным значением измеряемой физической величины. Она характеризует точность результатов измерений, производимых используемым средством.

По характеру проявления погрешности делят на три основных вида: систематические, случайные и грубые (промахи).

Систематические погрешности Δ_сист – составляющие погрешности измерений, сохраняющиеся постоянными или закономерно изменяющиеся при многократных измерениях величины в одних и тех же условиях.

Такие погрешности выявляют детальным анализом их возможных источников и уменьшают введением соответствующей поправки, применением более точных приборов, калибровкой приборов с помощью рабочих мер и т.п.

Результаты измерений, содержащие систематическую погрешность, относятся к неисправленным. При измерениях стремятся исключить или учесть влияние систематических погрешностей. Постоянные систематические погрешности обнаруживают только путем сравнения результатов измерений с другими, полученными с использованием более точных методов и средств измерения. В ряде случаев эти погрешности устраняют специальными методами измерений.

Метод замещения – это метод, при котором осуществляется замена измеряемой величины известной величиной, причем так, чтобы в состоянии и действии всех используемых средств измерений не происходило никаких измерений. Для реализации метода необходимо иметь регулируемую меру. Например, при взвешивании по методу Борда, усовершенствованному Д, И, Менделеевым, на чашку весов, предназначенную для взвешивания массы, устанавливают полный комплект гирь и уравновешивают весы произвольным грузом. Затем на чашку с гирями помещают взвешиваемую массу и снимают часть гирь для восстановления равновесия. Суммарное значение массы снятых гирь равно значению взвешиваемой массы. Такой вариант метода замещения позволяет не только исключить погрешность от неравноплечности весов, но и сохранить неизменной их чувствительность при взвешивании различных масс. Метол замещения применяют также при измерении электрического сопротивления при помощи моста и мер сопротивления; измерении силы света при помощи фотометра и эталонных ламп и т.д.

Метод противопоставления – это метод, при котором измерения производятся дважды, причем так, чтобы причина, вызывающая погрешность, оказывала противоположное действие при первом и втором измерениях.

Для определения погрешности от неравноплечности весов при взвешивании этим методом массу взвешивают два раза, меняя ее местами с гирями. Исправленное значение массы (с учетом погрешности) определяется по формуле:

,

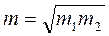где m₁, m₂- значения, полученные при первом и втором взвешиваниях.

Этим методом определяется одновременно и отношение плеч

,

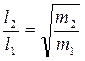которое используется в дальнейшем при обычном взвешивании в качестве поправочного коэффициента.

Случайные погрешности Δ_сл– составляющие погрешности измерений, изменяющиеся случайным образом по значению и знаку при повторных измерениях одной и той же физической величины в одних и тех же условиях. Данные погрешности проявляются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Отметим, что случайная погрешность уменьшается при увеличении количества измерений.

Факторы, определяющие возникновение случайных погрешностей, проявляются нерегулярно, в различных комбинациях и с интенсивностью, которую трудно предвидеть. Случайная погрешность случайно изменяется при повторных измерениях одной и той же физической величины. Для оценки интервала значений погрешностей и вероятности появления определенных значений необходимы многократные измерения и использования математического аппарата теории вероятностей.

Наиболее универсальный способ описания случайных величин заключается в отыскании их интегральных или дифференциальных функций распределения, а также определения по ним математического ожидания случайной величины (она представляет собой оценку истинного значения измеряемой величины), дисперсии результатов измерения, а также среднего квадратичного отклонения (СКО) результатов наблюдений.

Именно среднее квадратичное отклонение σ имеет размерность измеряемой величины и наиболее часто используется в качестве основного параметра, характеризующего рассеивание результатов измерений. В производственной практике часто считается необходимым выполнение следующего условия: допустимое предельное отклонение от заданного номинального размера должно быть на менее интервала 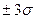. В этом случае в среднем только одно из 370 изделий будет бракованным. Область технологического рассеивания какого-либо размера (параметра) изделия, как правило, подчиняется нормальному закону, и периодически определяемое среднее квадратичное отклонение является показателем изменений в технологическом цикле

Грубые погрешности (промахи) – погрешности, существенно превышающие ожидаемые при данных условиях измерения. Они возникают из-за ошибок оператора или неучтенных внешних воздействий. В случае однократного измерения промах обнаружить нельзя. При многократных наблюдениях грубые погрешности выявляют и исключают в процессе обработки результатов наблюдений.

Итак, если не учитывать промахи, абсолютная погрешность измерения Δ представляет собой сумму систематической и случайной составляющих: Δ= Δ_сист + Δ_сл.

Порядок выполнения работы

Задание №1. Исключение систематических погрешностей методом замещения

1. Подготовьте в тетради таблицу:

Таблица №2

Масса тела m , г	Истинное значение массы тела m и ,г	Абсолютная погрешность Δ, г	Относительная погрешность δ, %

 

2. Уравновесьте весы.

3. Определите массу тела m с точностью до 0,01 г.

4. Освободите весы от гирь и груза.

5. Установите на чашку весов, предназначенную для взвешивания полный комплект гирь.

6. Уравновесите гири произвольным грузом (для этого в стакан насыпьте необходимое количество речного песка).

7. Поместите на чашку с гирями тело.

8. Снимите часть гирь для восстановления равновесия.

9. Найдите суммарное значение массы снятых гирь – оно равно значению взвешиваемой массы m_и..

10. Принимая значение m_и за истинное, определите абсолютную Δ и относительную погрешность δ измерений массы тела.

11. Результаты измерений и вычислений запишите в таблицу_2 .

Задание №2. Исключение систематических погрешностей методом противопоставления

1. Подготовьте в тетради таблицу:

Таблица №3

Масса цилиндра (правая чашка весов) m 1 ,г	Масса цилиндра (левая чашка весов) m 2 ,г	Истинное значение массы цилиндра m , г	Поправочный коэффициент km=l2 / l 1	Масса кубика М, г

 

2. Измерьте массу цилиндра, поместив его сначала на правую чашку весов m₁ .

3. Измерьте массу цилиндра, поместив его  на левую чашку весов m₂ .

4. Рассчитайте истинное значение массы по формуле

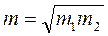
5. Рассчитайте поправочный коэффициент по формуле:

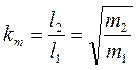
6. Измерьте массу кубика с учетом поправки:

M= k_mM_изм.

7. Результаты измерений и вычислений запишите в таблицу_3.

Задание №3. Изучение способов оценки случайных погрешностей измерений

1. Подготовьте в тетради таблицу:

 Таблица №4

Наименование величины	Номер образца
	№1	№2	№3	№4	№5	№6	№7	№8	№9	№10
Длина a, см
Ширина b, см
Высота c, см
Объем V, см3
Стандартный объем Vст, см3
Δ=׀ V- Vст,׀, см3

 

2. Обозначьте номера образцов.

3. Измерьте основные параметры (a, b, c) образцов с точностью до 0,1 мм, рассчитайте объем образцов.

4. Результаты запишите в таблицу 4.

5. Подчитайте количество разных N результатов определения объема тела.

6.  Подготовьте в тетради таблицу (число столбцов равно N+1):

Таблица №5

Наименование величины	Номера образцов
1	2	3	4	5	6	7	8
Объем V
Количество образцов, имеющих данное значение объема n
1	2	3	4	5	6	7	8
Вероятность P=n/10
Произведение V*P
Математическое ожидание M ( V )=∑ V * P
V2
V2*P
М( V 2 )=∑ V2*P
Дисперсия D(V)
Среднее квадратичное отклонение результатов измерения σ

 

7. Запишите в таблицу 5 различные значения объема измеряемой величины по возрастанию.

8. Укажите номера образцов, имеющих такое значение объема, подсчитайте их.

9. Рассчитайте вероятность P каждой величины.

10. Найдите математическое ожидание M ( V ) по формуле:

M ( V )= V ₁ * P ₁ + V ₂ * P ₂ +…+ V_n * P_n

11. Рассчитайте величину М( V ² ):

М (V²)=V₁²*P₁+V₂²*P₂+…+V_n²*P_n

12. Рассчитайте дисперсию D(V) по формуле:  

                                    D ( V )= М( V ² ) - M ² ( V )

13. Определите значение среднего квадратичного отклонения результатов измерения σ, как

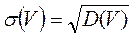
14. Сделайте вывод, какие образцы соответствуют условию, при котором .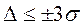

 

Контрольные вопросы:

1. Какие методы обнаружения систематических погрешностей вы знаете?

2. Какая величина используется в качестве основного параметра, характеризующего рассеивание результатов измерений?

Отчет о проделанной работе должен содержать:

наименование; цель; список оборудования; таблицы с результатами измерений и вычислений; формулы величин и их погрешностей; вычисления; вывод; ответ на контрольные вопросы.

 

 

Практическая работа №3