А.С. Михайлов
А.А. Попов
МОДЕЛИРОВАНИЕ систем
Утверждено редакционно-издательским советом СибГТУ
в качестве лабораторного практикума для студентов направлений
09.03.02 «Информационные системы и технологии»
профиль подготовки «Информационные системы и технологии в промышленности»,
09.03.04 «Программная инженерия»
профиль подготовки «разработка программно-информационных систем»
очной, очно-заочной форм обучения
Красноярск 2015
Михайлов, А.С. Моделирование систем: Лабораторный практикум для студентов подготовки 09.03.02 «Информационные системы и технологии» профиль подготовки «Информационные системы и технологии в промышленности», 09.03.04 «Программная инженерия» профиль подготовки «разработка программно-информационных систем»/ А.С. Михайлов, А.А. Попов – Красноярск: СибГТУ, 2015. - 82с.
Лабораторный практикум содержит 5 лабораторных работ по основным темам курса «Моделирование систем». Тематика лабораторных работ имеет профессиональную направленность. В конце каждой лабораторной работы имеются контрольные вопросы для проверки усвоения темы.
Рецензенты:
к. т.н, доцент, СФУ А.С. Кузнецов;
д. т.н, проф., СибГТУ Г.А. Доррер.
© ФГБОУ ВО “Сибирский государственный технологический университет”, 2015
©Михайлов А.С.
©Попов А.А.
Содержание
Введение. 5
1 Основные понятия. 6
2 Основы моделирования в среде AnyLogic. 14
Лабораторная работа № 1. Моделирование упрощенного калькулятора 18
Лабораторная работа № 2. Создание модели сердца «Heart». 27
3 Создание дискретно-событийных моделей. 37
Лабораторная работа № 3. Моделирование работы светофора. 37
4 О Библиотеке Моделирования Процессов. 50
Лабораторная работа № 4 Модель работы станции автосервиса 53
5 Пешеходная библиотека. 64
Лабораторная работа № 5 Модель « Пионерлагерь». 65
Приложение А (справочное) Ключевые слова. 81
Библиографический список. 82
Введение
Практикум предназначен для изучения предмета «Моделирование систем» студентами направлений 09.03.02, 09.03.04 очной, очно-заочной форм обучения, который изучается в 4-5 семестре.
В настоящее время моделирование составляет неотъемлемую часть современной фундаментальной и прикладной науки. Поэтому при изучении данного курса представляется целесообразным использовать современные пакеты прикладных программ, предназначенные для имитационного моделирования.
Лидером среди них является отечественный продукт AnyLogic, сочетающий в себе мощный инструмент объектно-ориентированного моделирования с интерфейсом визуального программирования.
Успешное освоение лабораторного практикума способствует формированию у студента следующих профессиональных компетенций:
для направления 09.03.02
ПК-5 – способность проводить моделирование процессов и систем;
ПК-12 – способность разрабатывать средства реализации информационных технологий (методические, информационные, математические, алгоритмические, технические и программные);
ОПК-2 – способность использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования.
для направления 09.03.04
ПК–12 - способность к формализации в своей предметной области с учетом ограничений используемых методов исследования;
ПК-14 - готовность обосновывать принимаемые проектные решения, осуществлять постановку и выполнение экспериментов по проверке их корректности и эффективности.
Основные понятия
Подобие модели объекту
Объект и модель находятся в отношении сходства, т.е. модель по каким-то признакам должна быть подобна изучаемому объекту. Это явление называют изоморфизмом (от греч. isos – равный и morphe – форма). Различают три вида подобия.
Первый вид подобия – подобное масштабирование. Примеры такого подобия: модели автомобилей, самолетов, кораблей сооружений и т.д.
Второй вид подобия – косвенное подобие (математическая аналогия). Удачный математический аналог из других областей знаний может сильно упростить построение модели и ее анализ. Так, очень многие физические процессы могут быть описаны уравнениями, общий вид которых q = – θ grad x (рисунок 1.1).
Перенос массы вещества – закон Фика:
j = –D · dС/dx,
где D – коэффициент диффузии; С – концентрация;
x – текущая координата.
Перенос тепла – уравнение Фурье:
q = –λ · dT/dx,
где q – тепловой поток; T – температура; λ – коэф
фициент теплопроводности.
Перенос электричества – закон Ома:
i = –c · du/dx,
где i – сила тока; c – характерная проводимость;
u – потенциал.
Рисунок 1.1 – Тройная аналогия процессов переноса
Аналогичны законы Кулона и всемирного тяготения.
Примером также может служить подобие электрических и механических явлений:
· колебание физического маятника:
· пружинного маятника;
· колебательного контура;
Третий вид подобия – условное подобие или подобие по соглашению. Примерами являются когнитивные модели (рисунок 1.2), географические карты, масштабированные чертежи сооружений, зданий, структурные схемы (модели системного анализа). При этом внешне сходство объекта и модели может не соблюдаться.
Рисунок 1.2 - Когнитивная модель потребления промышленной продукции (энергии, металлов и т.п.):
+ – положительные связи (влияния);
– – отрицательные связи (влияния).
Таким образом, объект моделирования и модель могут быть любой природы – материальными или абстрактными. Например, макет самолета – это материальная модель. Схема производства – абстрактная модель. Уравнения физики – это описание абстракций разных явлений материального мира. Модели могут быть и абстракциями других моделей. Наследование (создание одних классов на базе других) в объектно-ориентированном программировании наиболее характерный пример таких построений.
Адекватность модели
Вид и свойства будущей модели определяются целями исследователя, использующего этот инструмент. В модели отражаются свойства объекта, соответствующие этим целям, которые определяют и уровни детализации модели. В первую очередь должны быть определены существенные свойства оригинала, характеризующие его как некую проблему, которую нужно решить с помощью модели.
При этом стоит помнить, что знать все свойства предмета вашего исследования нельзя. К тому же не будем забывать, метод – это инструмент, а универсальных инструментов не бывает. Означает ли это, что моделирование – ненадежный помощник? Нет.
Во-первых, существует принцип множественности моделей. В соответствии с ним можно, а иногда – необходимо построить несколько моделей, позволяющих рассмотреть объект как проблему с различных позиций. К соответствующим решениям (моделям) можно идти, используя разные подходы. Например, создание модели поведения человека будет зависеть от разработки разных целей:
1) добиться антропоморфной кинематики компьютерной модели тела человека;
2) получить модель характерных психических реакций человека;
3) смоделировать реакции различных социальных групп людей.
Во-вторых, существуют специальные процедуры проверки, является ли модель точным представлением реальной системы, т.е., адекватна ли модель системе.
При верификации, т.е. проверке достоверности модели, определяется, правильно ли концептуальная модель (модельные допущения) преобразована в компьютерную программу.
Валидация – это процесс, позволяющий установить, является ли модель точным представлением системы для конкретных целей исследования. Определяющим моментом в этих процедурах является положение: «модель и ее результаты достоверны, если … руководители проекта признают их правильными». В итоге, если модель «адекватна», ее можно использовать для принятия решений относительно системы, которую она представляет, как если бы они принимались на основании экспериментов с реальной системой.
В-третьих, итоговый результат (т.е. «хорошая» или «плохая» модель получится) зависит от личности разработчика. Моделирование, как метод научного познания, предполагает творческий подход к объекту и целям исследования. В этом виде научного производства не обойтись без развитого воображения, умения анализировать и делать обобщения. Хорошие модели – это «минитеории» и их создание требует нестандартного мышления.
Общие сведения
Использование AnyLogic предоставляет уникальную возможность войти в мир моделирования, имея лишь базовую подготовку в области информационных технологий.
Это современная среда разработки моделей на языке Java с русскоязычным графическим интерфейсом и тщательно продуманной контекстной справочной системой. AnyLogic содержит большую библиотеку визуальных компонентов. Разработчик может также создавать и добавлять в среду собственные компоненты. Модели сохраняются как Java-апплеты. В профессиональной версии работает отладчик и можно создавать автономные JAR-файлы. AnyLogic - модели обладают хорошими средствами 2D–3D симуляции, интерактивности и развитыми возможностями проведения экспериментов (в том числе оптимизационных).
После установки программы нужно пройти регистрацию на сайте компании и получить ключ. Регистрация дает возможность получать от группы поддержки помощь в разработке моделей по Интернету, а также обновления программы. Необходимо отметить, что разработчики регулярно обновляют учебную версию AnyLogic Personal Learning Edition, сближая ее возможности с профессиональной версией более ранних релизов.
При запуске AnyLogic отображается начальная страница (рисунок 2.1). После этого можно выбрать пример из обширного списка учебных моделей и посмотреть ее работу.
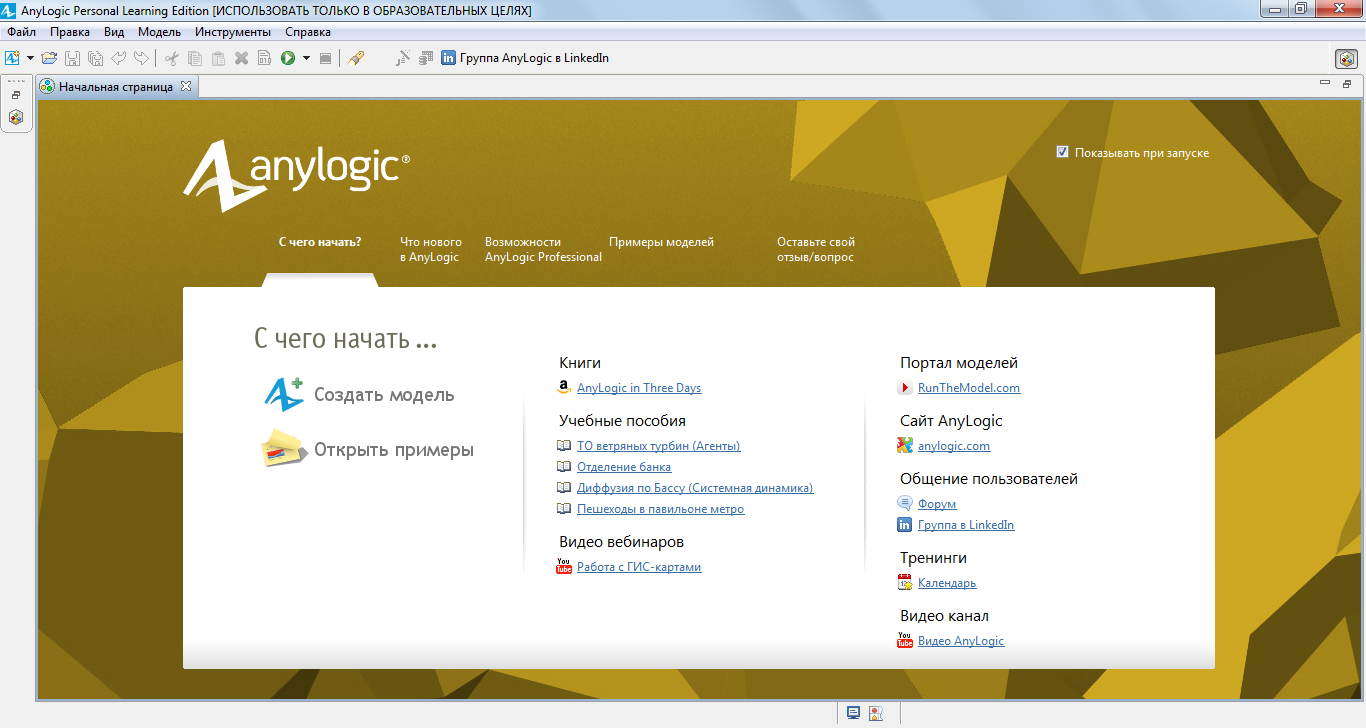
Рисунок 2.1 – Стартовая страница AnyLogic Personal Learning Edition 7
Другой вариант – закрыть стартовую страницу и начать работу «с нуля». Перед этим можно снять флажок у метки «Показывать при запуске», чтобы в следующий раз сразу же начинать работу с моделью.
Содержание работы
1) Последовательно выберем пункты меню Файл/Создать/Модель или щелкнем по пиктограмме палитры инструментов. Открывается диалоговое окно начальных настроек модели (рисунок 2.4).
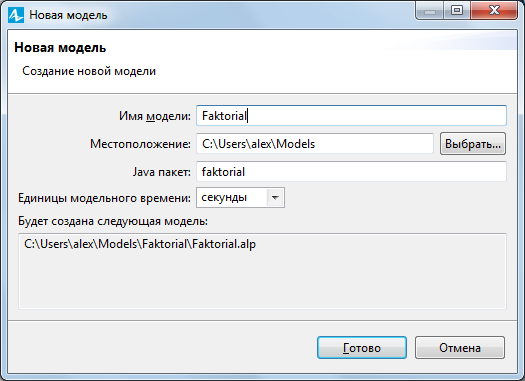
Рисунок - 2.4. Окно начальных настроек
По умолчанию AnyLogic предлагает имя проекта, в виде: Model#, где # – номер, соответствующий порядку создания модели.
Изменим его на Factorial и, если необходимо, выберем другое местоположение, где будут сохраняться все файлы модели. Поскольку используются язык Java, компоненты приложения (классы) собираются в пакеты. Таким образом, в AnyLogic можно создавать несколько моделей с разными именами, хранящих ресурсы в одном пакете. При попытке сохранить модель под новым именем, например, Factorial_1 – пункт меню Файл/Сохранить как – имя пакета по умолчанию останется прежним.
Если его не изменить (например на factorial_1), то появятся две модели с разными именами и общим пакетом. Одновременно работать с ними (загружать оба проекта) будет нельзя.
Нажмем кнопку Готово.
2) Первая переменная будет принимать значение n, набираемое с помощью кнопок. Раскроем закладку палитры элементов. Перетащим в окно графического редактора элемент Переменная, как показано на рисунок 2.6.
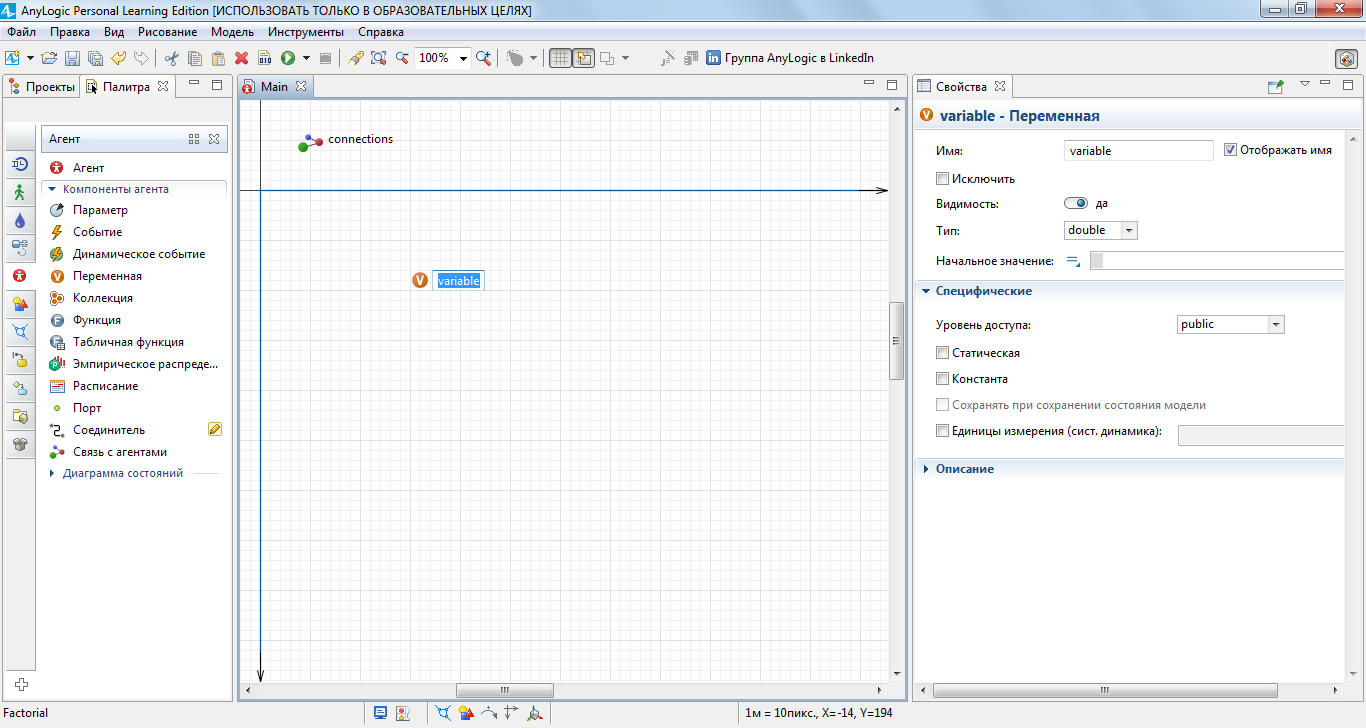
Рисунок - 2.6 Перетаскивание элемента Переменная в окно графического редактора
3) Изменим свойства переменой в соответствии с рисунок 2.7.
Рисунок - 2.7 Панель свойств переменной
4) Изменим имя со стандартного variable на n_Str. Учтем правила языка Java. Так как это объекты, их имена (а также имена методов) должны начинаться со строчной буквы. Всем переменным AnyLogic устанавливает по умолчанию тип double (вещественный) и начальное значение, равное нулю (если его не изменить, в поле Начальное значение не показывается).
В данном случае нужна переменная, которая будет хранить «число», набираемое кнопками, т.е. его изображением на табло должна быть строка (а не сумма) цифр, позиция которых будет соответствовать их разрядам.
Изменим тип переменной на String (строковый) и установим c помощью двух кавычек ее начальное значение («пустая строка»). В противном случае оно всегда будет null (так как это переменная ссылочного типа).
5) Введем в модель вторую переменную, которая будет принимать конечное значение параметра цикла, необходимое для вычисления факториала. Для этого повторим шаг 1. Изменим стандартное имя переменной на n. В свойствах переменной установим тип int (целый).
6) Добавим в модель элемент Текст из группы палитры инструментов Презентация. Он будет отображать на табло введенное кнопками число n. Внесем изменения на панели свойств (рисунок 2.8).
Рисунок 2.8 - Панель свойств элемента Текст (стрелками показаны измененные свойства)
7) Добавим в еще один элемент Текст. Назовем его textFact. Он будет показывать значение факториала на табло. Повторим для него операции шага 6. Выравнивание установим по левому краю.
8) Поместим в поле графического редактора кнопку из группы Элементы управления. Чтобы сразу получить убедительный результат вычислений, пусть это будет кнопка с цифрой «3» (3!=6) (рисунок 2.9).
9) Поместим в поле графического редактора еще одну кнопку. Потянув за угловой маркер, немного увеличим ее размеры. Результатом ее нажатия будет вычисление факториала и вывод результата на табло. Свойства кнопки и вид окна редактора модели показаны на рисунок 2.10.
Рисунок 2.9 - Панель свойств элемента Кнопка (стрелками показаны измененные свойства)
10) Впервые в модели появляется фрагмент кода на языке Java. Это всего лишь две строки. Первая изменяет значение текстовой переменной, вторая вызывает метод setText() элемента (объекта) textNum. При вычислении факториала невозможно напрямую использовать строковое представление числа в переменной n_Str, поэтому в первой строке кода «извлекаем» его с помощью класса-оболочки Integer и присваиваем результат переменной n. Вычисление факториала будем осуществлять с помощью цикла с параметром. В теле кода объявим вспомогательные переменные fact (тип вещественный) и параметр цикла i (целый), пробегающий значения от 1 до n.
Выполнение двух последних строк кода будет приводить к изменению соответствующих текстовых элементов. В textNum появятся значение n, символы «!» и «=». В textFact отобразится значение факториала.
Рисунок 2.11 - Вычисление факториала по щелчку кнопки
11) Запустим модель с помощью кнопки на панели инструментов или клавиши F5. Вначале откроется Окно настроек эксперимента (рисунок 2.11).
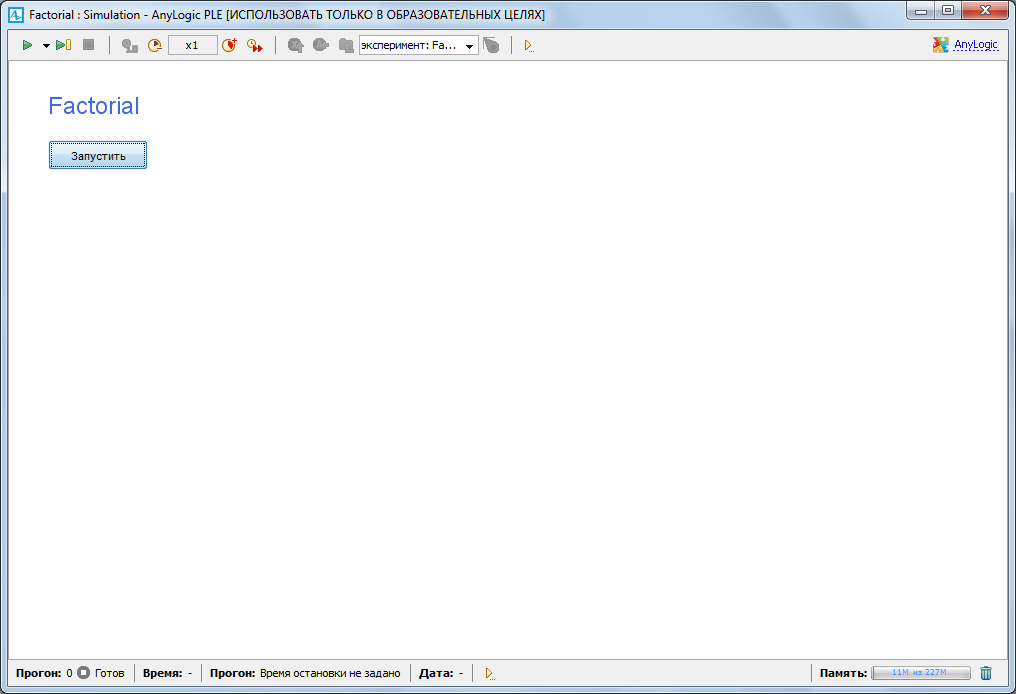
Рисунок 2.11 - Окно настроек эксперимента
Щелчком по кнопке запуска модели попадаем в Окно презентации. Модель работает. Последовательно нажимаем кнопки «3» и «n!». Текстовые элементы отображают корректный результат (рисунок 2.12).
Рисунок 2.12 - Вид окна работающей модели
Дальнейшие действия будут сводиться к добавлению кнопок, оформлению дизайна «калькулятора» и вида готового приложения.
12) Поместим элементы в соответствующие позиции. Цифровые кнопки «размножим» с помощью операций последовательного копирования-вставки уже имеющейся у нас кнопки «3». Они будут наследовать ее свойства, включая размеры и код. Необходимо изменить пункты свойств Имя кнопки, Метка и Действие (код). Так, для кнопки «0», код действий примет вид:
n_Str+=0;
textNum.setText(n_Str);
13) Напишем фрагмент кода для кнопки «С» (Clear):
n_Str="";
textNum.setText("n_Str ");
textFact.setText("");
Щелчок по ней приведет к начальным значениям строковой переменой n_Str и двух текстовых элементов, отображающих ввод n и вывод n!
Состояние модели на данном этапе показано на рисунке 2.13.
Рисунок 2.13 – Вид модели на шаге 13
14) Окончательная стадия разработки модели. Поместим в окно графического редактора элемент Скругленный прямоугольник из палитры Презентация. Он будет выполнять функцию электронного табло калькулятора. Подгоним его размеры под ширину клавиатуры. Чтобы он не закрывал текстовые элементы, щелчком правой клавиши мыши вызовем контекстное меню Порядок–На задний план.
В свойствах Радиус уменьшим радиус углов с 10 до 5 (рисунок 2.14).
Проделаем аналогичные действия с двумя другими прямоугольниками, которые будут имитировать корпус калькулятора. В свойствах первого прямоугольника уберем заливку.
Немного увеличим размер второго прямоугольника.
Настройка приложения. Переместим переменные за пределы область показа, например, влево от оси Y. Выделим мышью все элементы калькулятора и передвинем их немного вниз и влево.
В панели проектов мышью щелкнем по элементу Simulation:Main, затем по frame (рамка). Рядом с окном графического редактора появится закладка Simulation. Для показа калькулятора и работы с ним вместе с необходимыми полями, достаточно области размером 350 точек по горизонтали и 400 по вертикали. Изменим Свойства рамки в соответствии с этими значениями, затем скорректируем другие элементы. В окончательном варианте приложение примет вид, как на рисунке 2.15.
Рисунок 2.14 – Настройка электронного табло
Рисунок 2.15 - Окончательный вариант модели
Цель работы:
· Научиться создавать модели с нуля.
· Создавать графики в презентации модели.
· Создавать слайдеры для управления параметрами модели.
Содержание работы
Мы рассмотрим простейшую математическую модель, описывающую процессы, похожие на биение сердца. Эта модель описана двумя дифференциальными уравнениями первого порядка:
где: х – радиус сердца, х0 – его начальное значение, b – переменная, а ε – параметр eps.
В этой модели мы исследуем характер зависимостей переменных х и b от времени при разных значениях параметра eps, а также построим фазовую диаграмму зависимости радиуса х от переменной b.
1) Для построения нового проекта щелкните кнопку Создать панели инструментов, либо выберите в основном меню Файл / Создать / Модель. В появившемся диалоговом окне установите рабочую папку, наберите heart как имя модели и щелкните Далее. В следующем окне оставьте выбранным по умолчанию Начать создание модели с «нуля» и щелкните Готово. Новый проект под названием heart будет создан.
2) В нашей модели должны присутствовать две переменные состояния – х и b, и два параметра – х0 и eps, где х0 - начальное значение х. Начальное значение переменной b зададим константой.
В модели переменная х определяется дифференциальным уравнением:
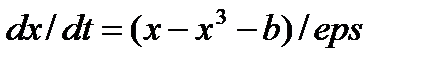
с начальным значением х, равным х0. В AnyLogic можно подобные зависимости задавать именно в таком аналитическом виде. Для того чтобы таким образом определить переменную х, зададим ее в форме накопителя.
Для этого перетащите мышью элемент Накопитель, расположенный во вкладке Системная динамика панели Палитра на диаграмму класса активного объекта Heart. Пиктограмма появится в поле редактора с именем stock. Одновременно внизу вместо окна свойств объекта Heart появится окно свойств выделенного накопителя. В это окно в поле имени Имя вместо предопределенного имени stock введите х и нажмите клавишу <Enter>.
В поле Начальное значение введите x 0, после чего, определим формулу для вычисления х в поле dx / dt следующим образом:
.
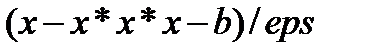Поле Начальное значение будет недоступным. Для того чтобы ввести в это поле формулу, нужно выбрать Режим задания уравнения Произвольный, см. рисунок 2.16.
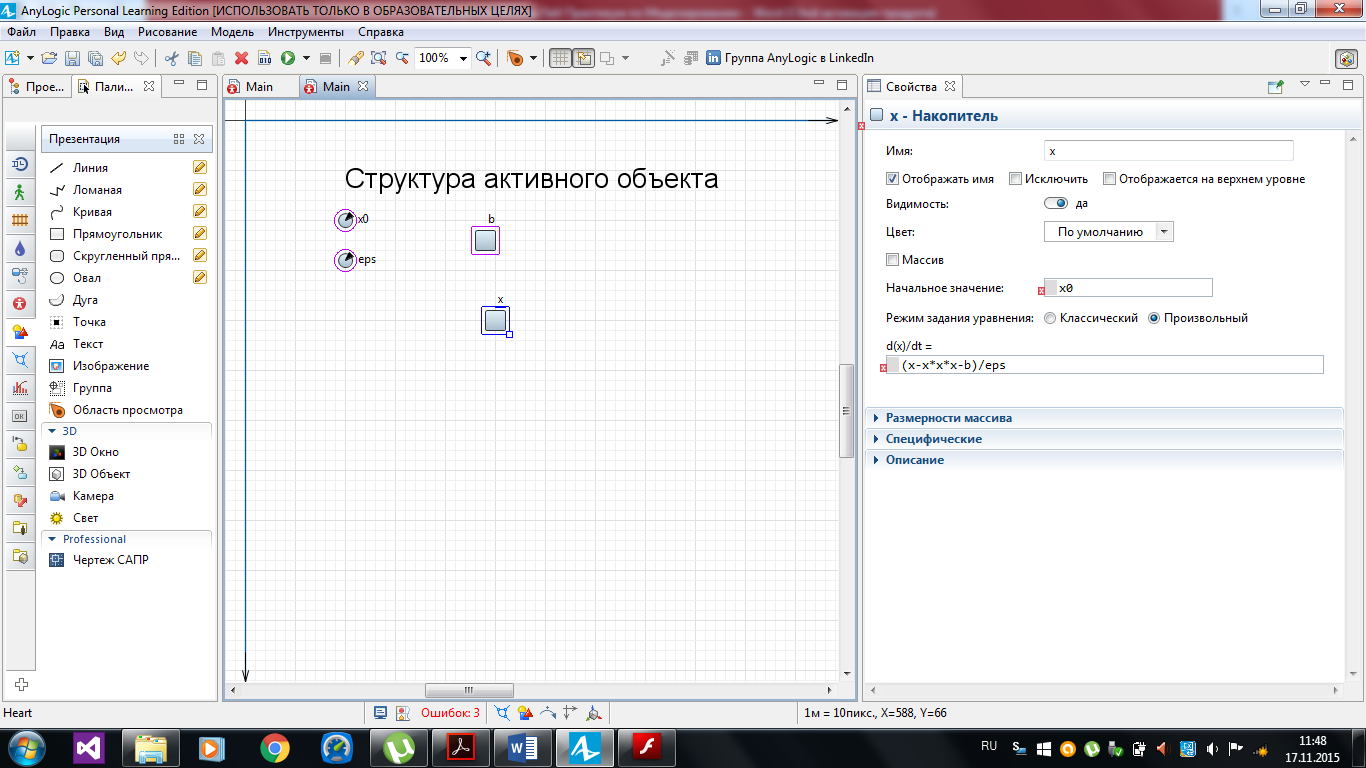
Рисунок 2.16 – Накопитель х
При выделенной пиктограмме накопителя его имя можно перемещать по диаграмме класса. Саму пиктограмму накопителя также можно перемещать при нажатой на ней левой кнопке мыши.
3) Вторая переменная b задана дифференциальным уравнением
db/dt = х – х0. Ее создадим в модели аналогичным образом (рисунок 2.17). Установим начальное значение b равное 0. В поле Начальное значение окна свойств переменной b величину 0 можно не записывать: если это поле пусто, по умолчанию значение переменной считается нулевым.
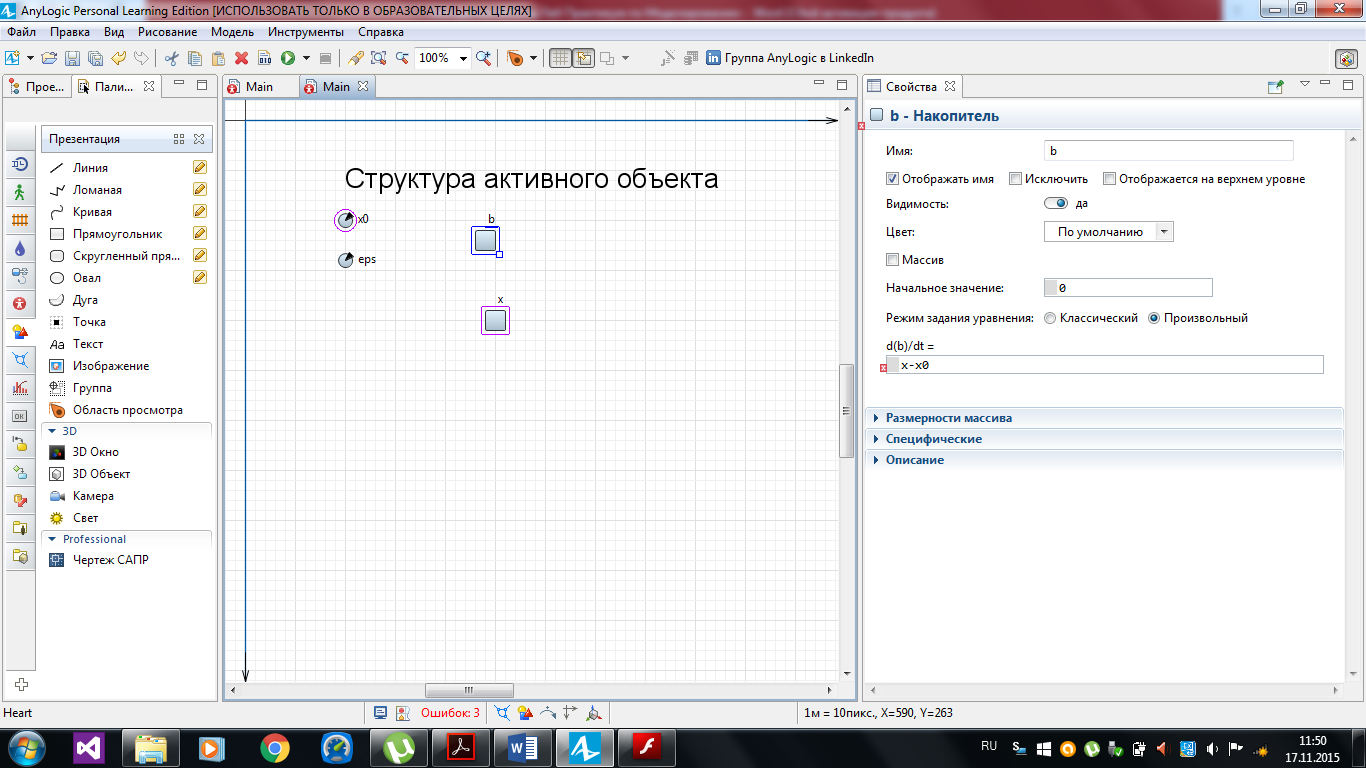
Рисунок 2.17 – Накопитель b
4) На диаграмму класса активного объекта можно помещать текстовые комментарии. Для этого перетащите элемент Текст со вкладки Презентация панели палитр на диаграмму класса, рядом с накопителями. Введите следующий комментарий: Структура активного объекта. Его можно редактировать в поле Текст окна свойств этого комментария.
5) Для проверки правильности синтаксиса (модели можно использовать кнопку Построить модель панели инструментов или нажать клавишу F7. Если щелкнуть на этой кнопке, то выполнится компиляция разрабатываемой модели в программный код на языке Java. Щелкните по кнопке Построить модель. В нашем примере обнаружились ошибки (рисунок 2.18): действительно, нами не определены параметры х0 и eps.
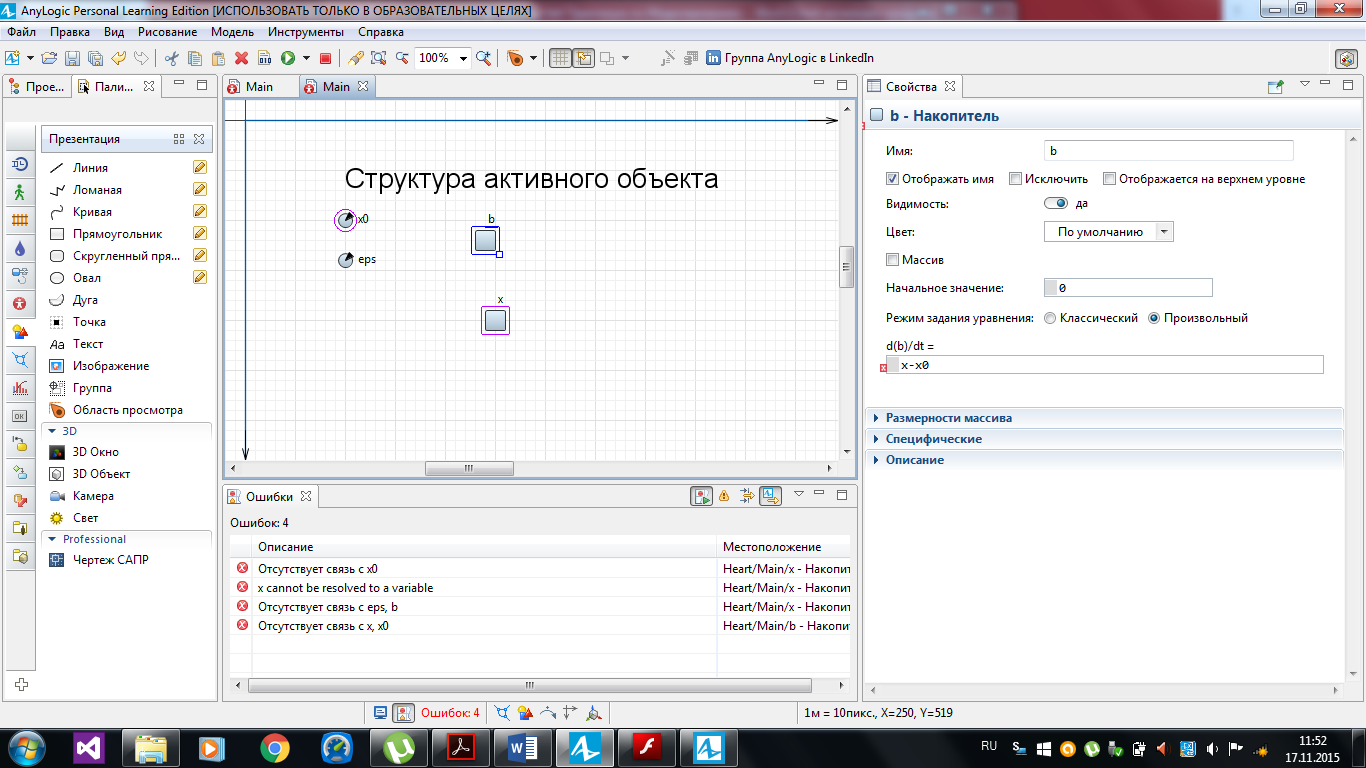
Рисунок 2.18 – Ошибки при запуске
6) На наличие ошибки указывает появившиеся символы [х] в панели Ошибки. Для каждой ошибки показывается ее описание и местоположение - имя элемента модели, при задании которого эта ошибка была допущена. Двойной щелчок мышью по ошибке, в зависимости от того, где она была совершена, приведет к открытию того или иного редактора или панели. Если, например, это графическая ошибка, то будет открыт графический редактор, отображающий диаграмму соответствующего класса активного объекта, в котором будут выделены фигуры, которые были неправильно нарисованы.
7) Для завершения построения модели указанные пропущенные параметры нужно задать. Пусть х0 = 0.5, eps = 0.01. Перетащите мышью пиктограмму Параметр с вкладки Основная панели Палитры на диаграмму класса активного объекта Heart. Назовите его х0, затем на вкладке Основные панели свойств этого параметра введите в поле Значение по умолчанию – 0.5. Остальные поля оставьте без изменения. Переменная eps со значением 0.01 задается так же. Снова выполните проверку синтаксиса: нажмите кнопку Построить модель.
8) Задайте связи, как показано на рисунке 2.19.
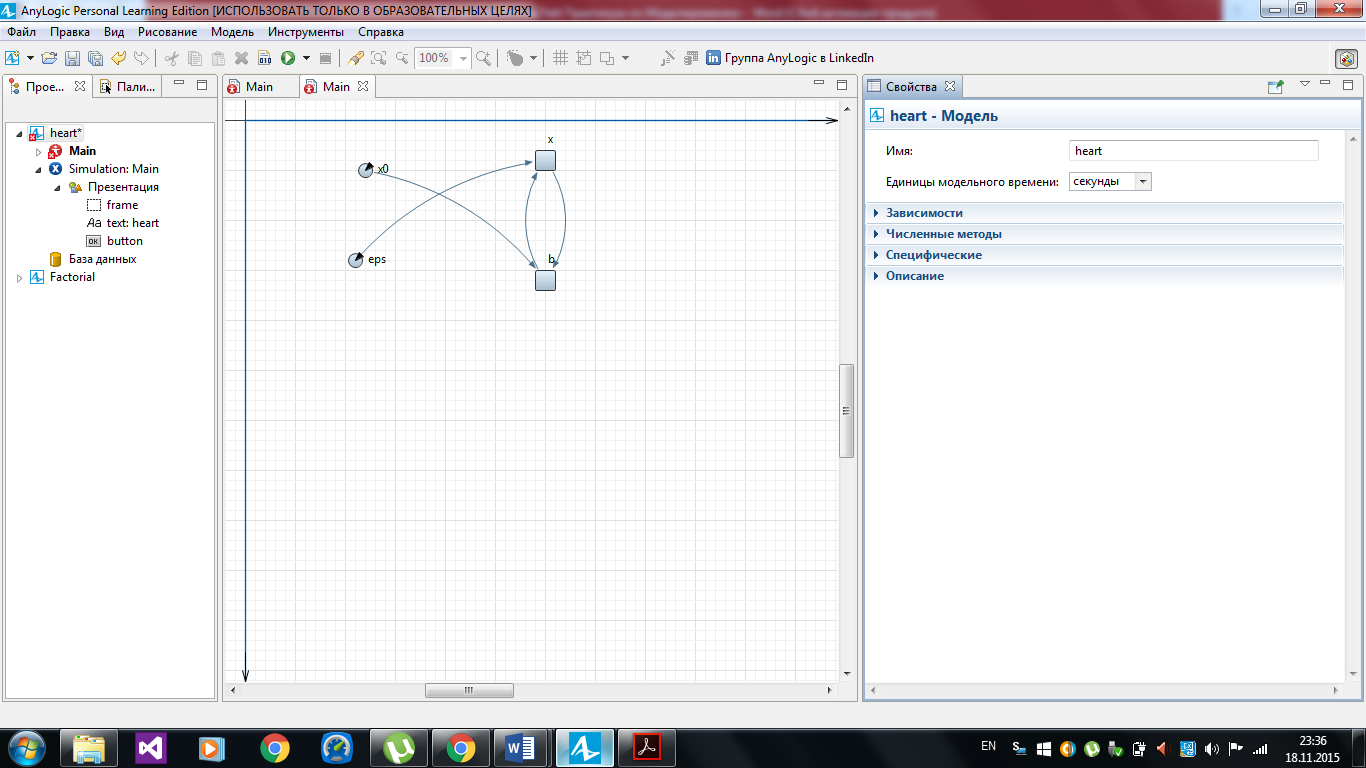
Рисунок 2.19 – Связи переменных
9) Щелкнув на кнопке запуска модели, после компиляции откроется окно презентации эксперимента. Запустив эксперимент, увидим структуру активного объекта: переменные и параметры с их значениями (рисунок 2.20). Переменные b и х в этом окне начнут изменяться в соответствии с определенными для них уравнениями.
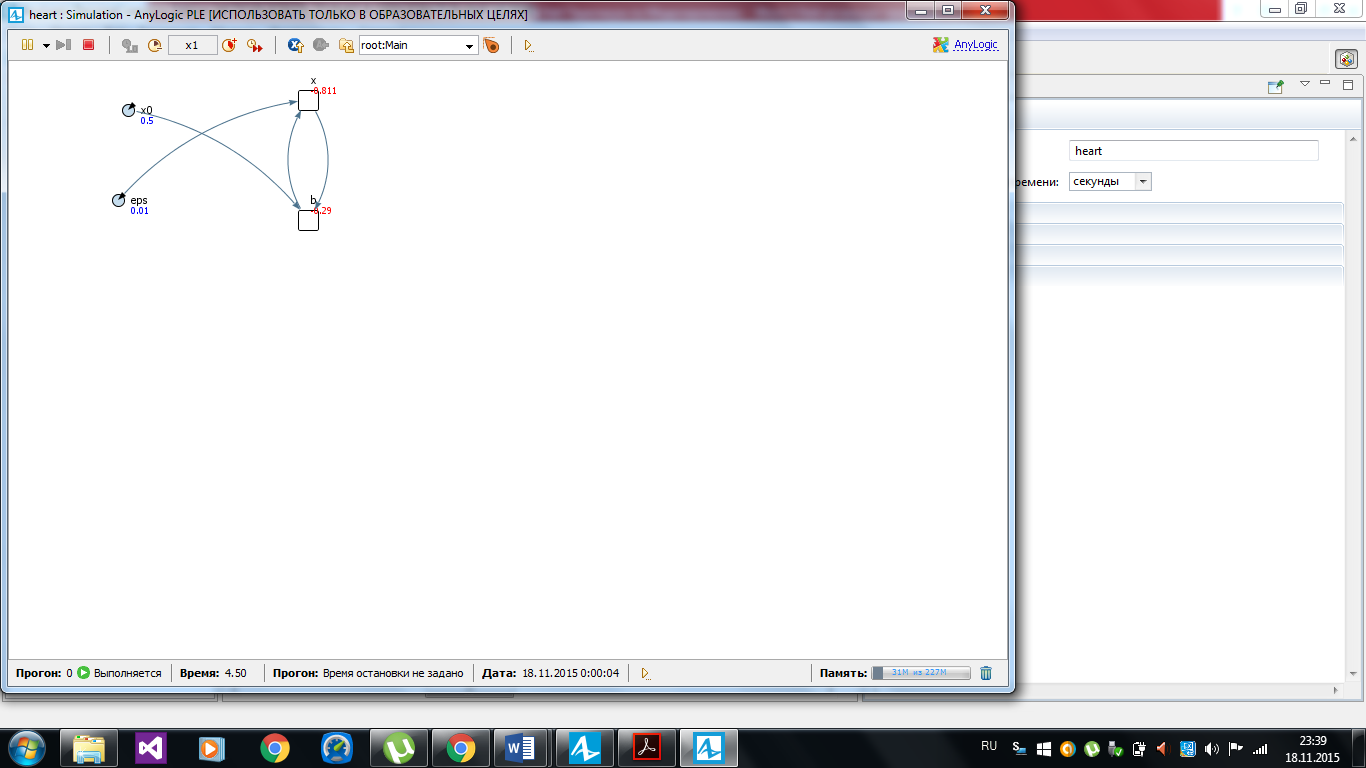
Рисунок 2.20 – Результат запуска модели
10) Системы дифференциальных и алгебраических уравнений, при выполнении модели, решаются одним из встроенных численных методов. Сам метод и необходимая точность решения выбираются автоматически, но можно изменить предварительные установки: во вкладке Проект выбираем нужную модель, в свойствах модели – Численные методы (рисунок 2.21).
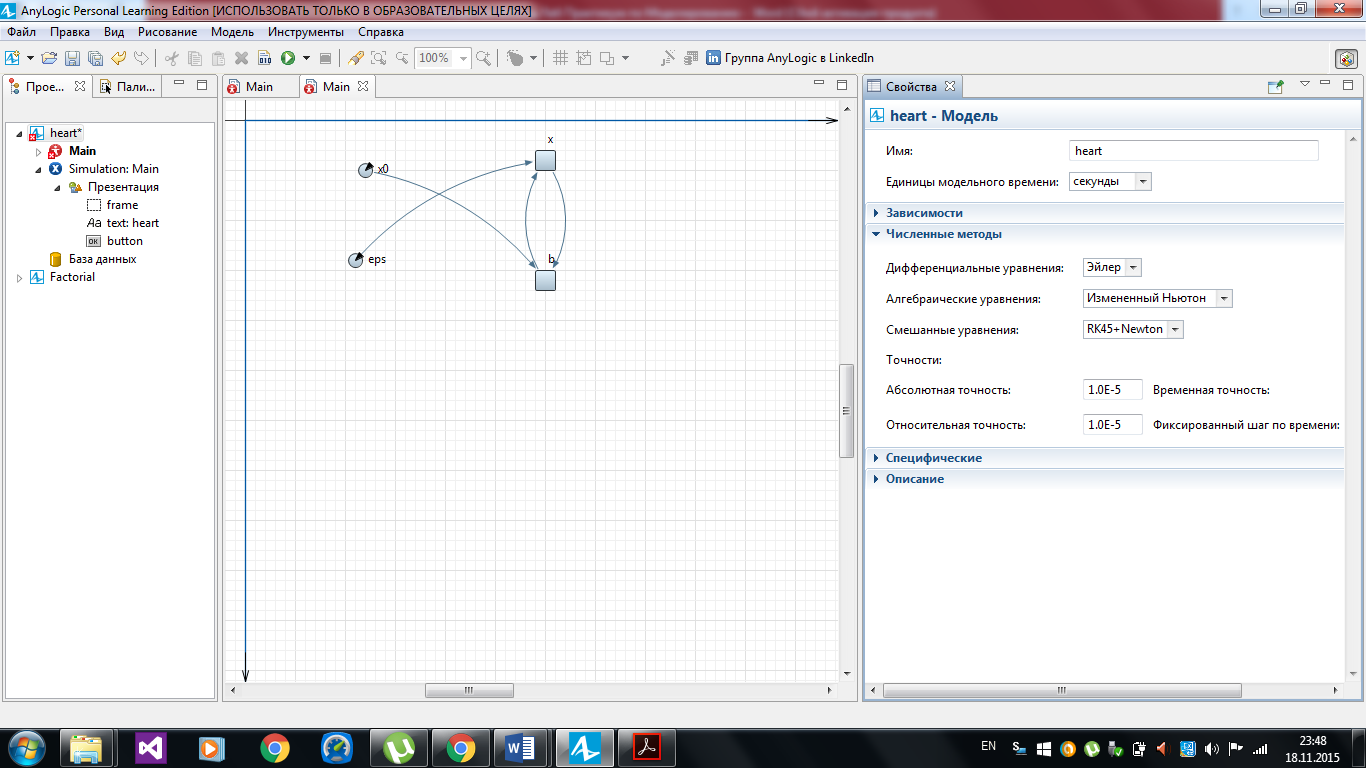
Рисунок 2.21 – Выбор метода и необходимая точность решения
11) AnyLogic позволяет наглядно представить поведение модели, в частности, представить изменения во времени всех ее переменных. Для получения полнофункциональных графиков лучше воспользоваться диаграммами AnyLogic, которые позволяют динамически визуализировать данные, собираемые в результате работы модели. Набор диаграмм схож с тем, что предлагается программой MS Excel.
Построим графики зависимостей переменных b и х от времени и фазовую диаграмму b от х. Перетащите элемент График из палитры Статистика в то место графического редактора, где Вы хотите нарисовать график. Перейдите на страницу Данные панели Свойства (рисунок 2.22).
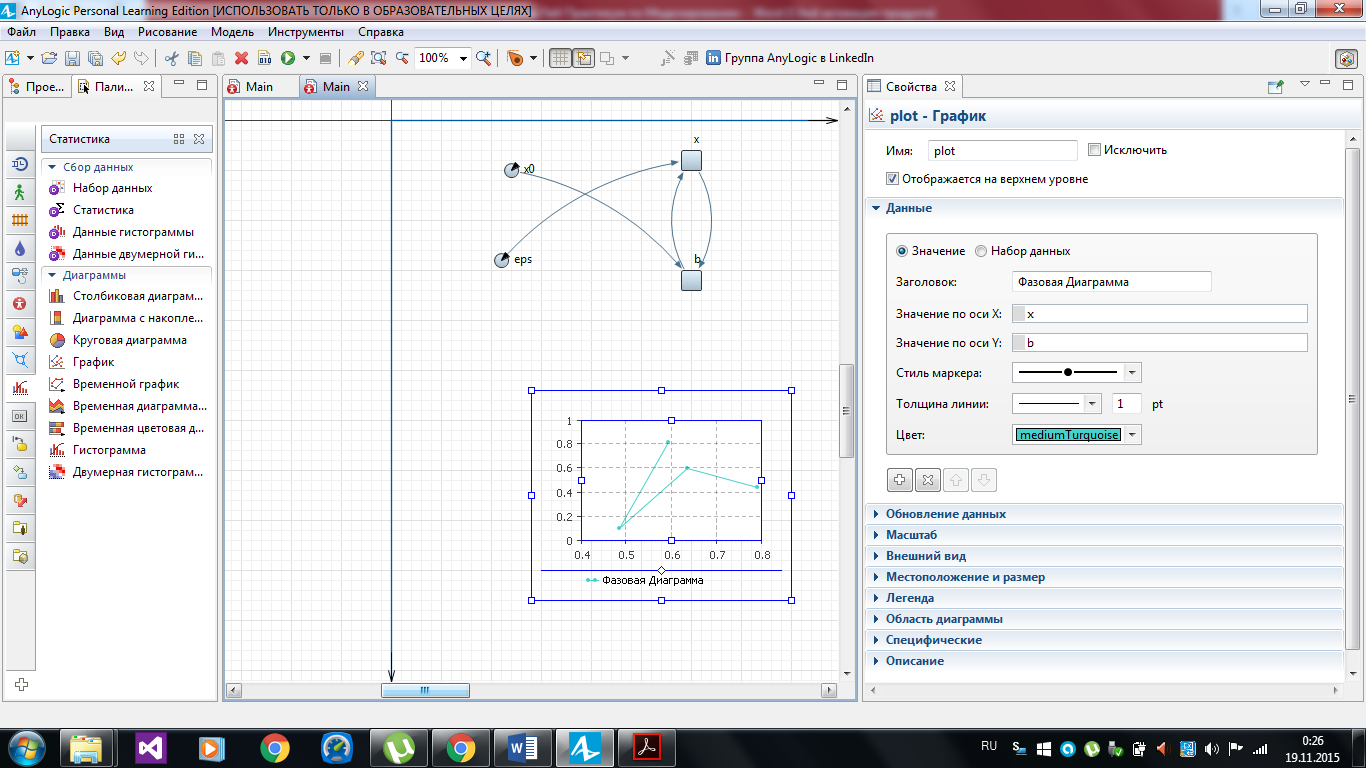
Рисунок 2.22 – Свойства графика
12) Щелкните мышью по кнопке Добавить элемент данных. При этом над кнопкой появится новая секция свойств, задающая настройки нового элемента данных, который будет отображаться на данном графике. В поле Значение по оси Х введите имя переменой х, а в поле Значение по оси Y – имя переменной b. Задайте заголовок Фазовая диаграмма для этого элемента данных в поле Заголовок. Для того чтобы получить гладкую диаграмму нужно уменьшить период обновления данных в поле Период.
13) Аналогично постройте временной график для переменных x и b, разместив их на одном графике. Временной диапазон укажите равным 10
14) Для лучшего понимания динамики модели и наблюдения за процессами, в AnyLogic можно строить анимированные изображения, состоящие из динамических элементов. Графические элементы называются динамическими, поскольку все их параметры - координаты, размер, цвет и даже их видимость – в процессе выполнения модели можно сделать зависимыми от переменных и параметров, которые меняются со временем при выполнении модели.
Остановите выполнение модели и вернитесь на диаграмму класса Heart. Прямо на диаграмме мы будем рисовать презентацию сердца.
15) Перенесите элемент Овал из палитры Презентация, представляющий динамику сердца на диаграмму класса. Статические значения его параметров задайте так: в панели свойств овала на вкладке Основные цвет заливки определите бордовым, цвет линии границы - красным; толщину линии границы установите 2.
Изменение объема сердца представим радиусами овала как функции от переменной х, как показано на рисунке 2.23.
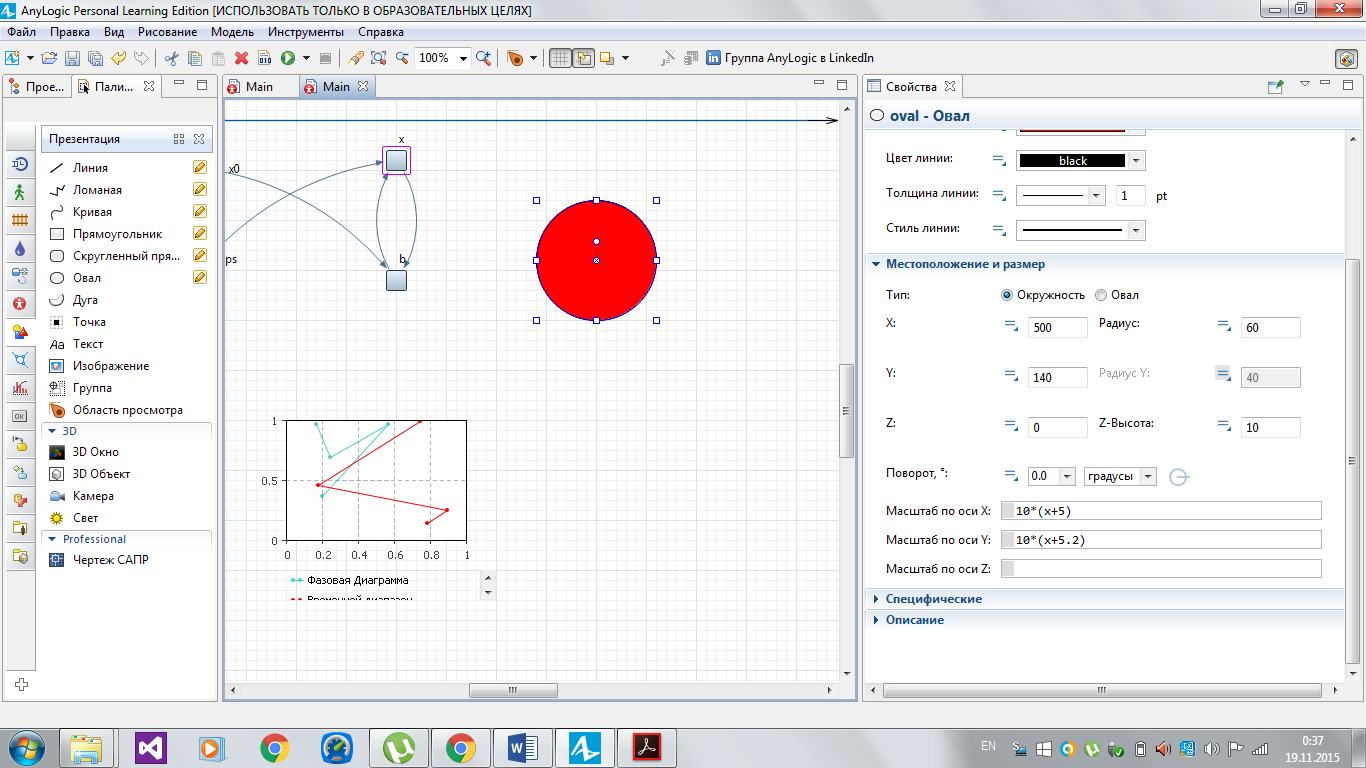
Рисунок 2.23 – Настройки «сердца»
16) В AnyLogic существует элемент управления, позволяющий графически выбирать число из заданного диапазона значений путем перетаскивания рукоятки – бегунок.
Бегунки или их еще называют слайдеры, обычно используются для изменения значений численных переменных и параметров во время выполнения модели.
Перетащите мышью с палитры Элементы управления пиктограмму Бегунок на диаграмму класса Heart между структурой и анимационным овалом. В поле Связать с панели свойств введите имя параметра x0, а минимальное и максимальное значения, которые можно регулировать слайдером, установите 0 и 1. Добавить подписи к слайдеру можно простым нажатием кнопки Добавить метки, рисунок 2.24. Запустите модель и проверьте действие слайдера.
Аналогично сделайте слайдер для параметра eps, установив ограничения от 0.01 до 0.5. (рисунок 2.24)
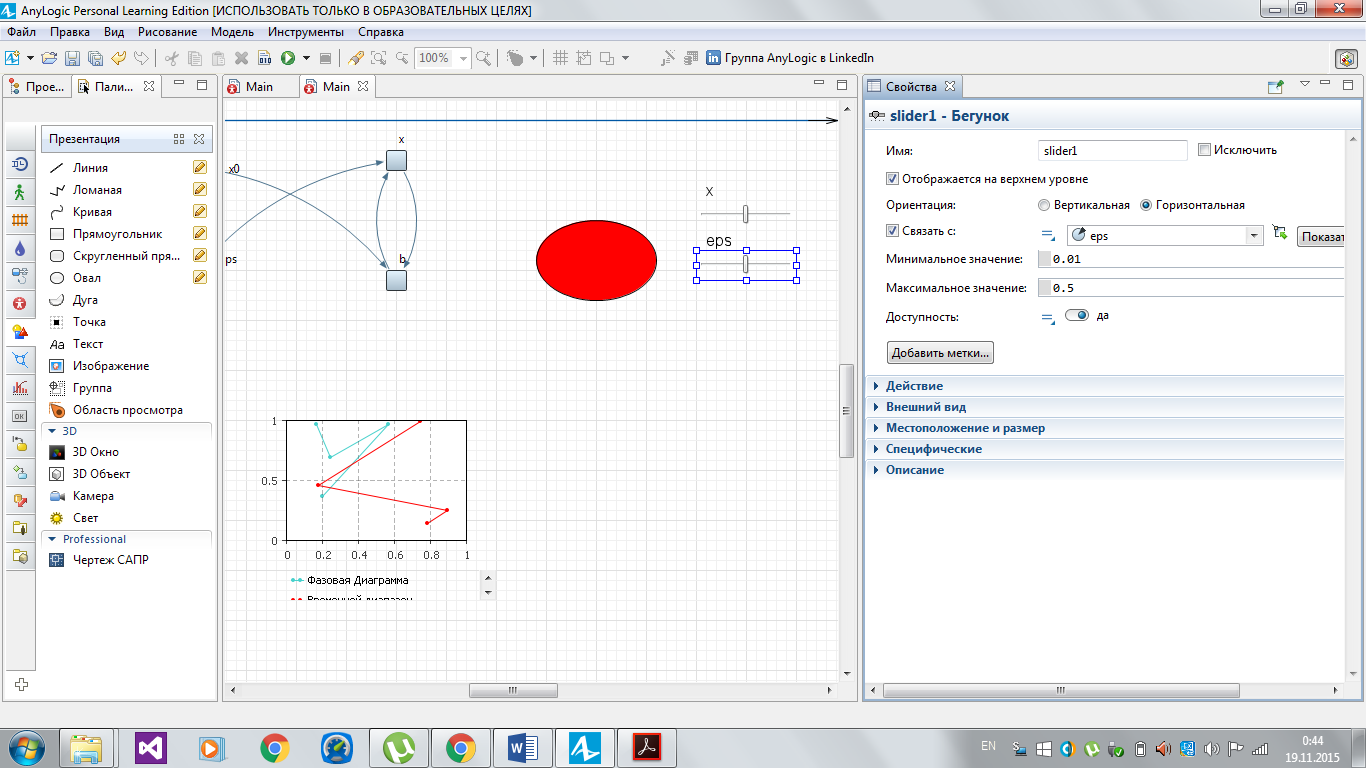
Рисунок 2.24 – Настройки элементов управления
17) В верхнюю часть диаграммы класса Heart введите поясняющий текст. Для этого перетащите мышью пиктограмму Текст с палитры Презентация. В поле Текст введите текст Модель сердца, выберите шрифт Century Gothic, стиль Полужирный, размер 22. Установите также координаты (Х, Y) этого объекта (20,10). В правой верней части презентации добавьте еще одно поле Текст и напиши в нем пояснения как на рисунке 2.25 о содержании нашей модели.
Введите в поле презентации прямоугольники, как показано на рисунке 2.25, и поместите их на задний план, чтобы они выделяли функциональные блоки построенной модели. Для того чтобы фигура была фоном и не закрывала другие изображения, в контекстном меню данного прямоугольника выполните команду Порядок / На задний план.
Сделайте подписи к слайдерам, чтобы было понятно, какими параметрами мы управляем.
Рисунок 2.25 – Внешний вид презентации Main модели.
Контрольные вопросы
1 Как поместить на поле презентации текущее значение времени?
2 Как создать переменную, определяемую дифференциальным уравнением?
3 Как какими параметрами должен иметь связи накопитель?
4 Как выбрать численный метод решения дифференциального уравнения?
5 Как ввести в модель слайдер и связать его с переменной?
6 Как изменить период обновления графика?
7 Как создавать текстовые поля и выводить в них нужные переменные динамически?
Цель занятия
· построение стейтчартов;
· действия при входе и выходе из состояния, иерархические состояния;
· переход по исчерпании таймаута;
· переход при получении сообщения.
Содержание
Построим модель регулируемого пешеходного перехода со светофором, разрешающим или запрещающим движение транспорта.
Описание проблемы
Светофор, регулирующий движение автомобилей на пешеходном переходе, может находиться в следующих состояниях: движение транспорта разрешено (зеленый), приготовиться к запрещающему сигналу (мигающий зеленый), приготовиться к остановке (желтый), движение запрещено (красный) и приготовиться к движению (красный и желтый).
Светофор работает в автоматическом режиме. В каждом состоянии светофор находится определенный постоянный период времени.
Построение модели
Создайте новый проект под названием Svetofor и назовите класс корневого активного объекта Model.
Наша модель будет иметь только один активный объект, представляющий светофор, поэтому корневой объект Model будет единственным активным объектом нашей модели. На диаграмму класса активного объекта Model поместите Начало диаграммы состояний из панели Диаграмма состояний и назовите ее Для_автомобилей, заметьте, что AnyLogic может работать с элементами, набранными кириллицей. Перетащите мышью элемент Состояние под стрелочку начала диаграммы как показано на рисунке 3.1.
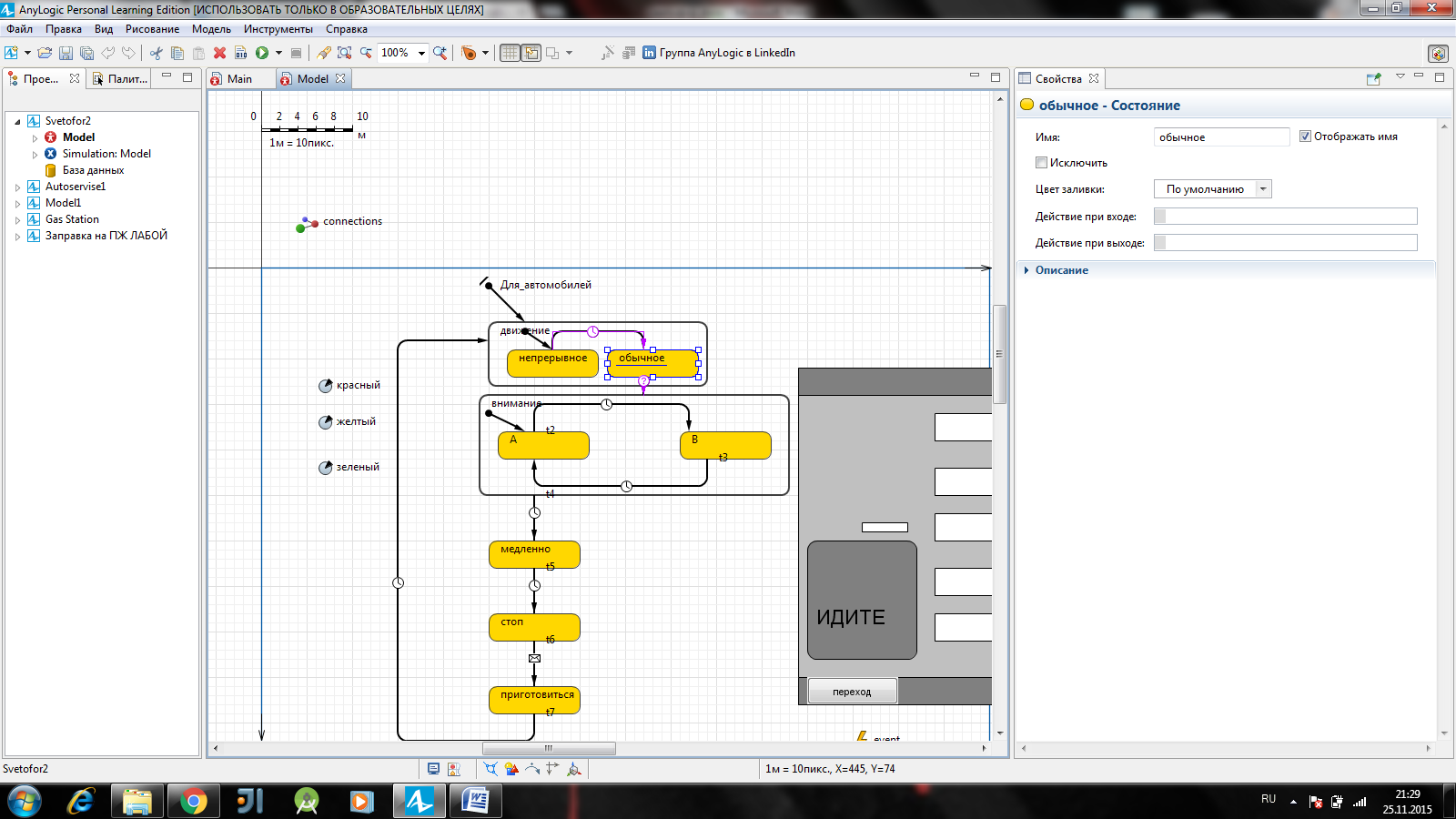
Рисунок 3.1 – указатель начального состояния
Имя состояния, как и все другие его параметры, можно редактировать в окне его свойств. Для того чтобы построить стейтчарт, следует использовать элементы из палитры Диаграмма состояний, рисунок 3.2.
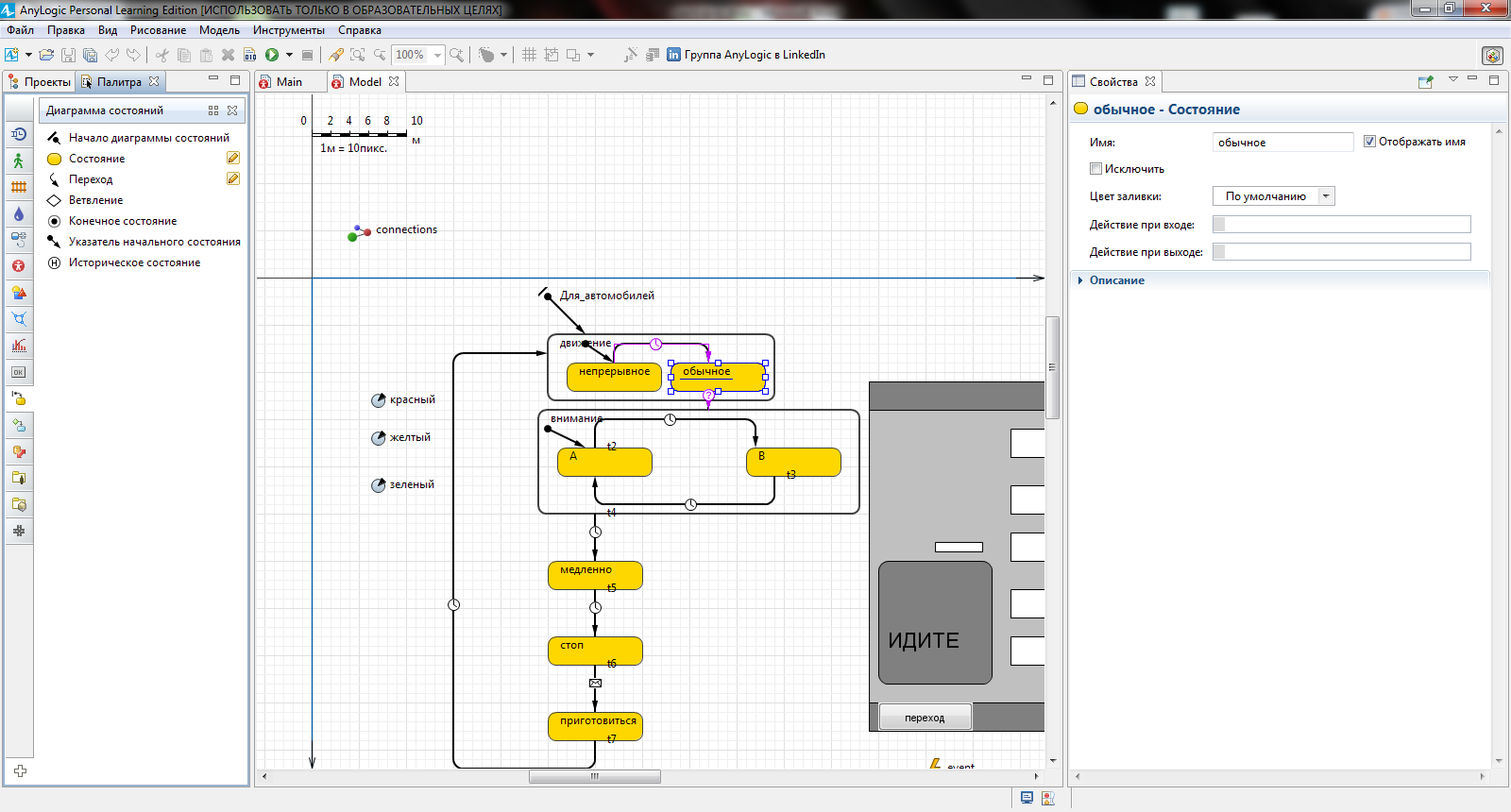
Рисунок 3.2 – Библиотека диаграмм состояния
1. определяет начальное состояние всего стейтчарта.
2. с помощью кнопки рисуются состояния (как простые, так и гиперсостояния).
3. используется для рисования переходов между состояниями.
4. определяет начальное состояние внутри сложного состояния.
5. используется для рисования состояния, являющегося "финальным" в поведении активного объекта.
В соответствии с алгоритмом работы светофора помимо начального состояния в модель нужно ввести дополнительные состояния (рисунок 3.3). Начальное состояние назовите движение – движение автомобилям разрешено (зеленый свет), затем светофор переходит в состояние внимание – внимание (мигающий зеленый), медленно – приготовиться к остановке (желтый свет), остановка транспорта стоп – запрет движения (красный свет) и приготовиться – приготовиться к движению (красный и желтый свет горят одновременно).
Состояние внимание представим гиперсостоянием с парой переключающихся элементарных состояний: в одном из них зеленый горит (состояние А), в другом – нет (состояние В). Для построения гиперсостояния сначала создайте обычное состояние, увеличьте его (растянув мышью) и поместите внутрь другое состояние. Постройте эти состояния и соедините их переходами, как показано на рисунок 3.3.
Зададим условия срабатывания переходов. Переходы в нашем автоматическом светофоре выполняются по таймауту, т. е. по истечении интервала времени, который прошел с момента прихода системы в данное состояние.
1. В состоянии движение светофор находится 10 секунд.
2. Затем 7 секунд зеленый сигнал мигает (состояние внимание).
3. В состоянии медленно 4 секунды горит желтый сигнал.
4. В течение 10 секунд движение запрещено (состояние стоп).
5. 4 секунды светофор находится в состоянии приготовиться.
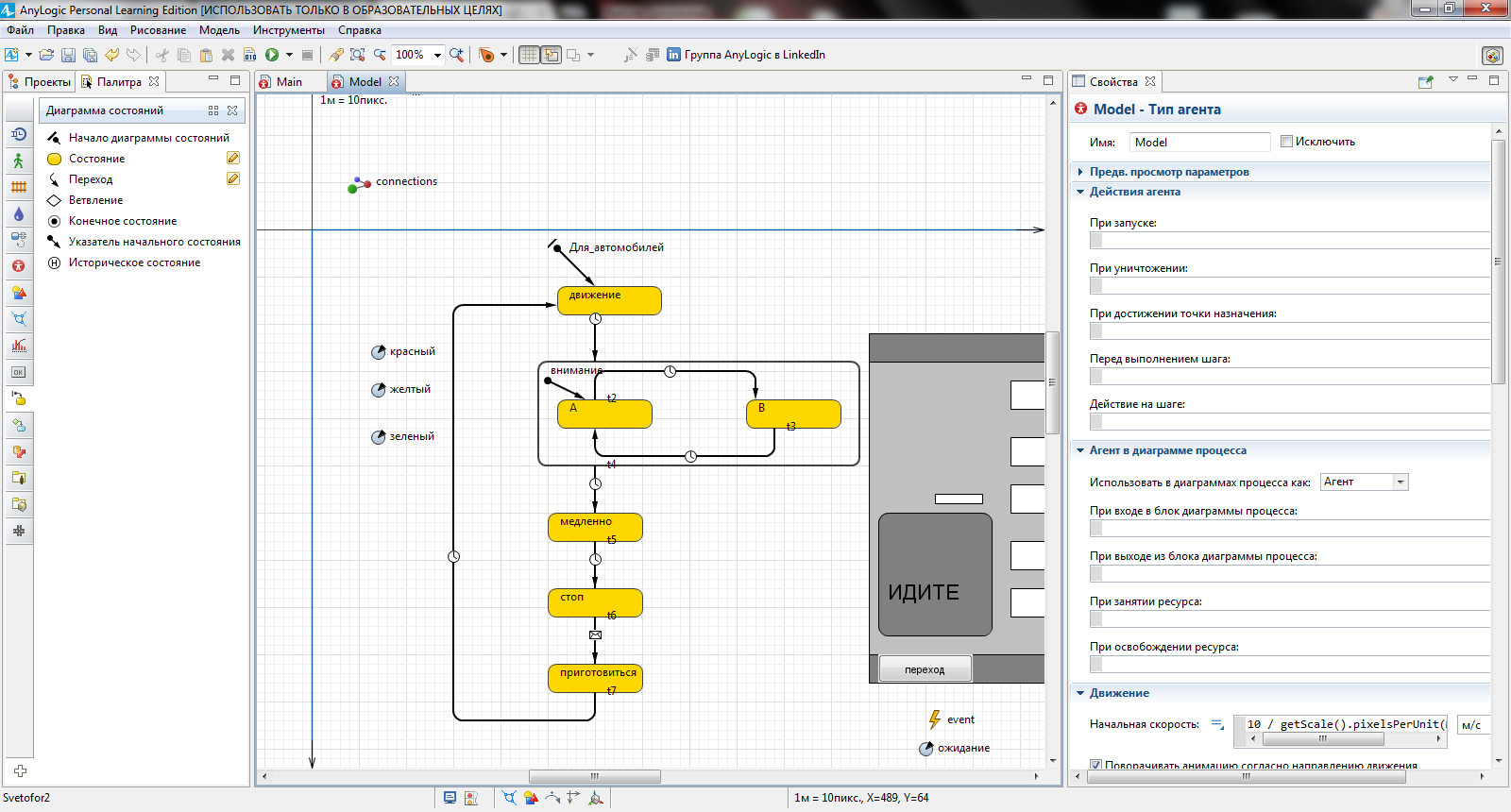
Рисунок 3.3 – Алгоритм автомобильного светофора
В нашей модели единица модельного времени соответствует 1 секунде реального времени.
Для задания условий срабатывания переходов, выделите переход t1, и в поле Происходит оставьте без изменения вариант По таймауту, а в поле По таймауту введите 10 (рисунок 3.4).
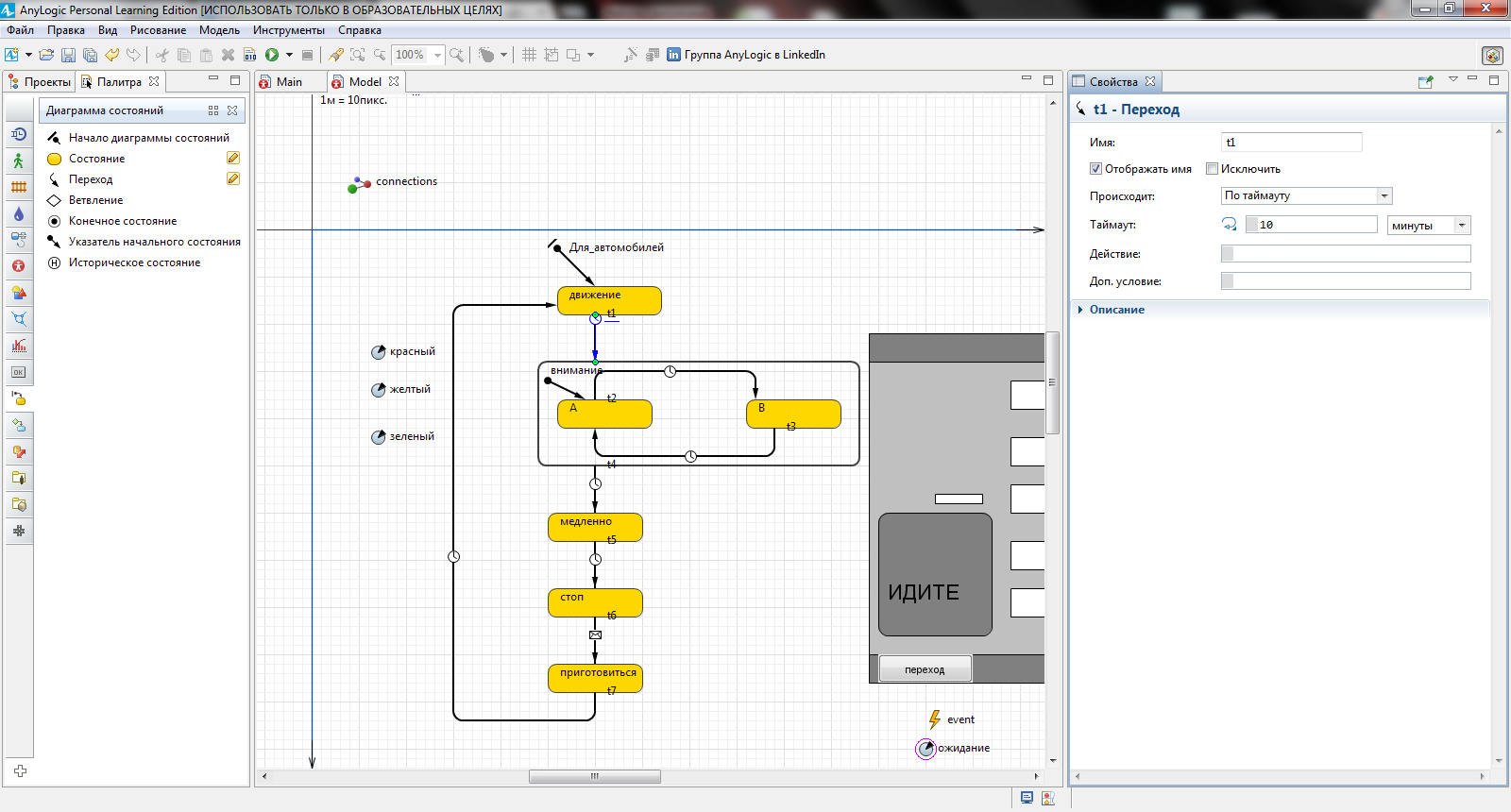
Рисунок 3.4 – свойства перехода t 1
Создайте три параметра логического типа: красный, желтый и зеленый, которые будут принимать истинное значение тогда, когда у светофора горит соответствующий сигнал: красный, желтый или зеленый (рисунок 3.5). Начальные значения этих булевых параметров можно не задавать: по умолчанию они будут равны false.
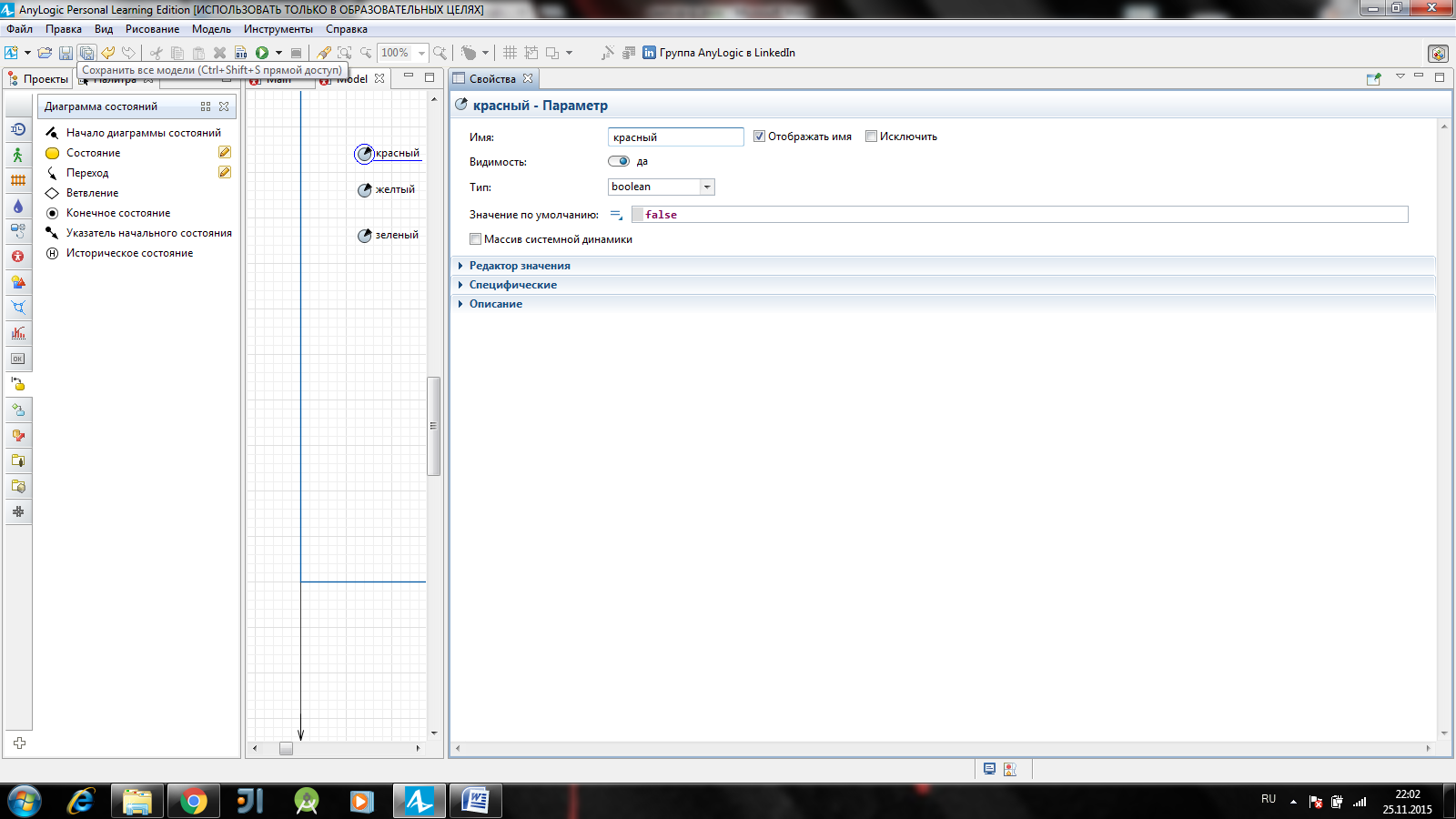
Рисунок 3.5 – настройка параметров
Мы создали стейтчарт именно для управления значениями этих параметров, каждое состояние отвечает за зажигание своего света или их комбинации. Например, в состоянии медленно должен гореть желтый, в состоянии стоп должен загореться красный свет, а в состоянии приготовиться должны гореть красный и желтый одновременно. Запрограммируем эти действия.
1. В свойствах состояния движение в поле Действие при входе запишите зеленый=true;, а в поле Действие при выходе запишите зеленый = false; (рисунок3.6).
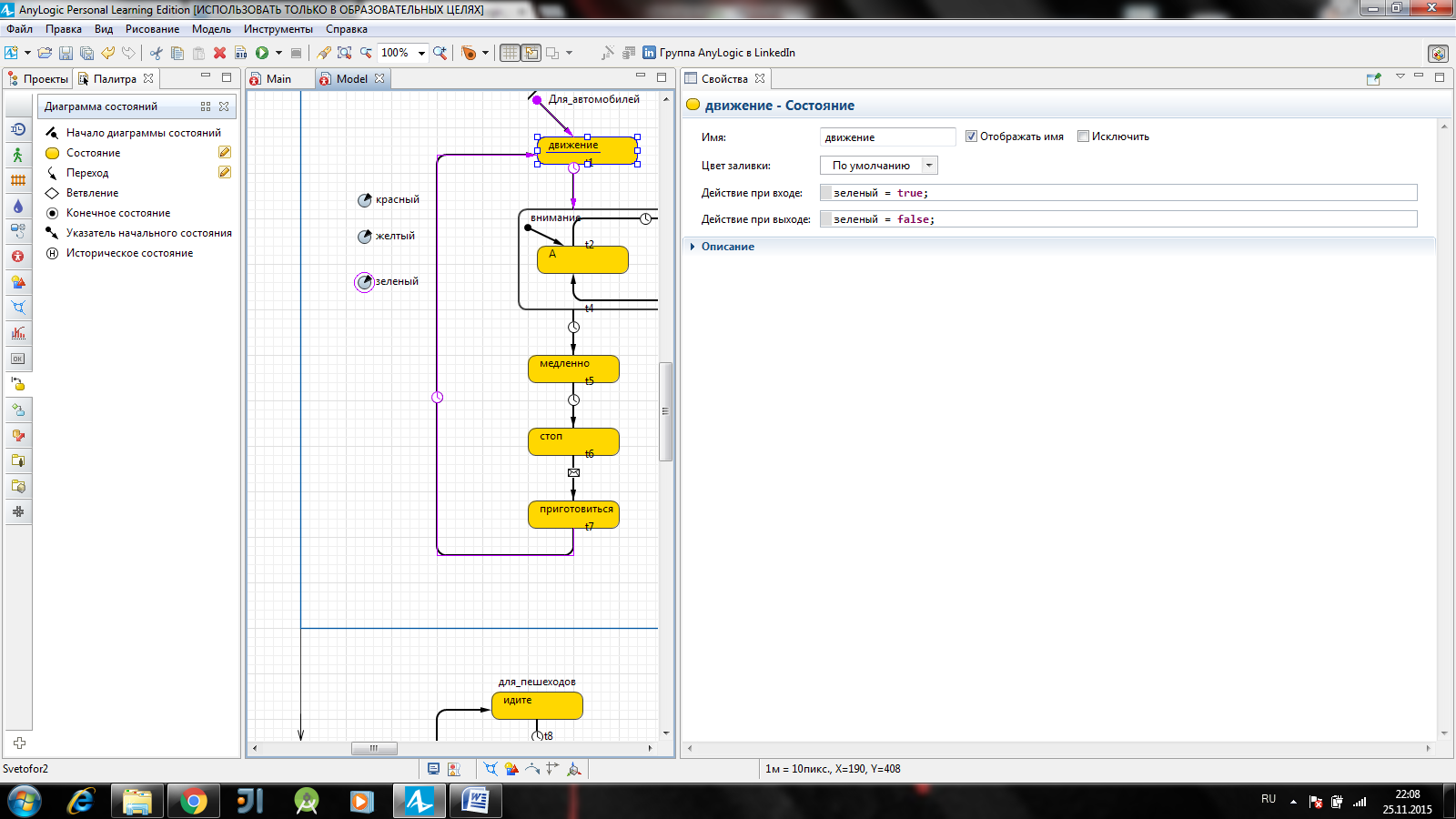
Рисунок 3.6 – настройка состояния «движение»
2. То же самое запишите для гиперсостояния внимание, а у состояния А эти поля нужно оставить пустыми – когда светофор находится в этом состоянии, он не горит.
3. Аналогично, в состоянии медленно нужно включить желтый сигнал, т. е. при входе в это состояние установить параметр желтый в true, а при выходе из этого состояния установить его в false.
4. Для состояния стоп аналогично опишите состояния параметра красный, а для состояния приготовиться оба параметра красный и желтый нужно установить в true при входе, и в false при выходе.
Запустите модель на выполнение. Вы увидите, что параметры зеленый, желтый и красный будут переключаться между значениями true и false в соответствии с алгоритмом переключения светофора.
Презентация модели
Презентация модели рисуется в той же диаграмме (в графическом редакторе), в которой задается и диаграмма моделируемого процесса, (рисунок 3.7). Графические объекты цвета сигналов светофора в презентации имеют динамические параметры, все остальные – статические. Проезжую часть удобно нарисовать с помощью графических примитивов типа Прямоугольник, а светофор с помощью примитива - Ломаная. Сигнальные элементы светофора строятся из трех овалов, повернутых на 45 градусов (поле Поворот вкладки Дополнительные окна свойств овала).
Установим динамическое значение цвета верхнего сигнала светофора (цвет верхнего овала): если переменная красный истинна, то цвет должен быть red (красный), в противном случае его цвет нужно установить gray (серый). Это записывается следующим условным выражением на языке Java:
красный? red: gray
Цвет среднего и нижнего овалов, следует установить в поле их динамических значений соответственно так:
желтый? yellow: gray
зеленый? green: gray
red, yellow, green и gray – предопределенные константы, обозначающие стандартные цвета. Запустите модель и проверьте ее работу.
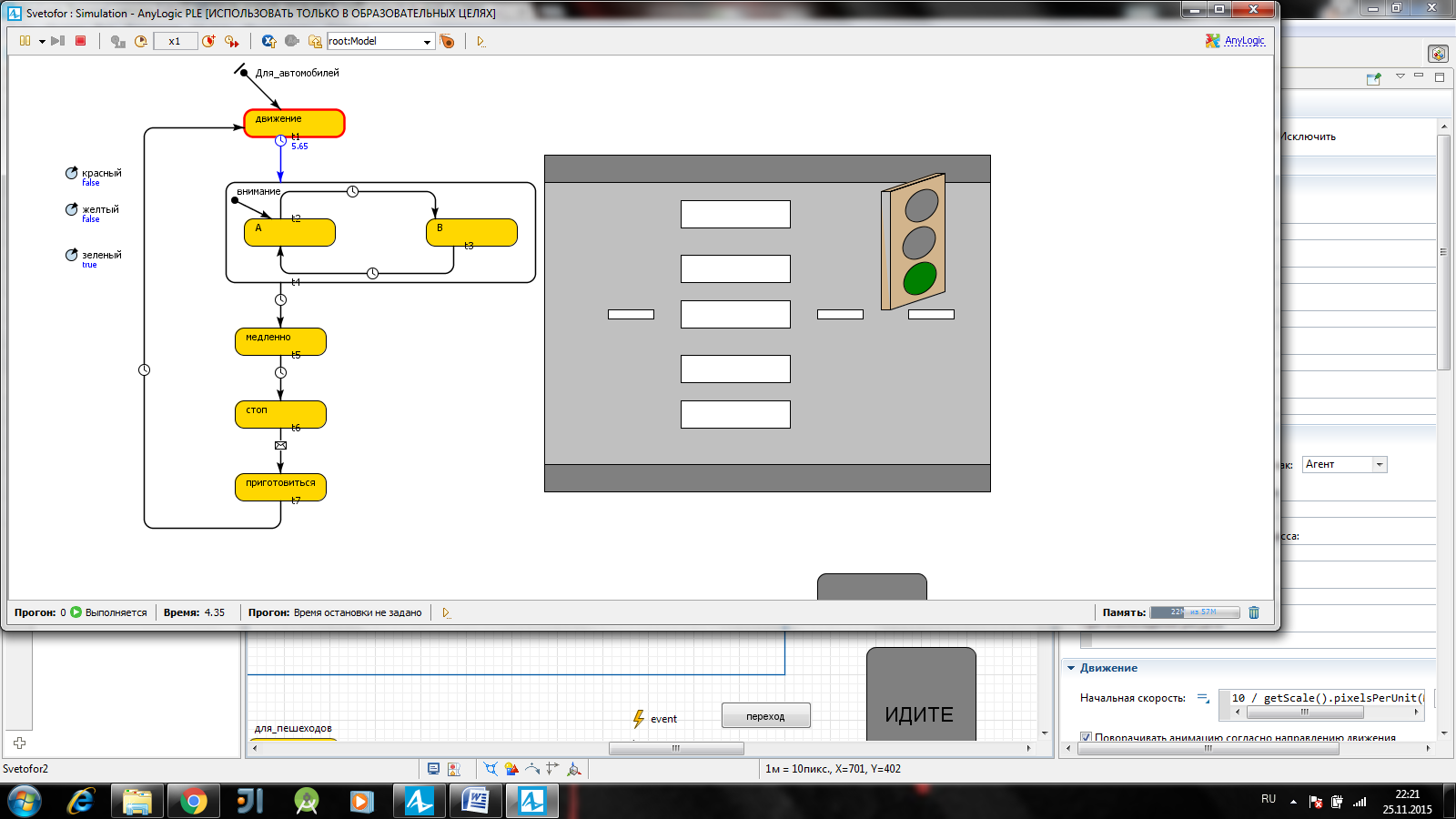
Рисунок 3.7 – модель автомобильного светофора
Содержание работы
Создание рабочего поля сети
Требуется спроектировать модель обслуживания автомобилей в авторемонтном предприятии. Такая модель представляет собой модель СМО, которую можно построить, используя сетевые элементы палитры «Библиотека моделирования процессов».
Для построения модели требуется создать новую модель с нуля.
Предварительно в поле активного класса модели необходимо поместить графическое изображение, которое будет представлять собой план территории авторемонтного предприятия. Чтобы подложить план, нужно использовать элемент Изображение из палитры Презентация. В качестве изображения выбирается файл layout.png, который был нами заготовлен заранее. После загрузки изображения нужно активизировать флажки Исходный размер и Блокировать, для того чтобы при рисовании сети (линий по которым будут двигаться заявка и ресурсы от узла к узлу) мы не могли редактировать план автосервиса (подложку).
Затем следует разместить на плане территории области, которые будут использоваться при моделировании работы СМО.
Эти области показаны на рисунке 4.1.
Чтобы создать эти области, используйте элемент Прямоугольный узел из палитры Разметка пространства. Разместите эти области в соответствии с рисунком 4.1. Присвойте областям идентификаторы с помощь вкладки Свойства вписывая их в поле Имя:
С помощью элемента путь из этой же палитры соедините прямоугольные вершины нашей сети network как показано на рисунке 4.2.
Чтобы смоделировать завершение осмотра автомобиля, нужно разместить точку выхода из автомастерской. Это точка отмечается точечным узлом в палитре Разметка пространства – позиция 7. Разместите точечный узел и присвойте ему имя wihod. Соедините его с нашей сетью network. В структуре проекта автоматически появляется группа графических элементов network , содержащая все точечные и прямоугольные вершины и пути, которые мы нарисовали на подложке с помощью палитры Разметка сети.
| 3 |
| 2 |
| 1 |
| 7 |
| 4 |
| 5 |
| 6 |
1- waitingHall (помещение ожидания для прибывших автомобилей));
2- staffRoom (комната отдыха для ремонтников, проводящих осмотр);
3- storageRoom (комната для хранения инструментов ремонтников);
4- procRoo m (комната осмотра автомобилей);
5- procRoom1 (комната осмотра автомобилей);
6- procRoom2(комната осмотра автомобилей);
7- wihod (выезд отремонтированных автомобилей).
Рисунок 4.1 - План автосервиса
Автомобили пребывают в помещение ожидания свободного ремонтника, затем свободный ремонтник сопровождает автомобиль для осмотра и берет необходимые ему инструменты. Какое-то время ремонтник находятся в одной из ремонтных комнат вместе с автомобилем (происходит ремонт автомобиля), затем ремонтник вместе с инструментом уходит в инструментальную комнату, где оставляет инструмент и затем возвращается в комнату отдыха мастеров. Автомобиль покидает автосервис в точке wihod . Маршруты по которым агенты и ресурсы перемещаются из узла в узел Anylogic выбирает самостоятельно по кратчайшему пути в сети network.
Важно чтобы в любой узел мы могли попасть по сети из любого узла по линиям сети (чтобы сеть была связной).
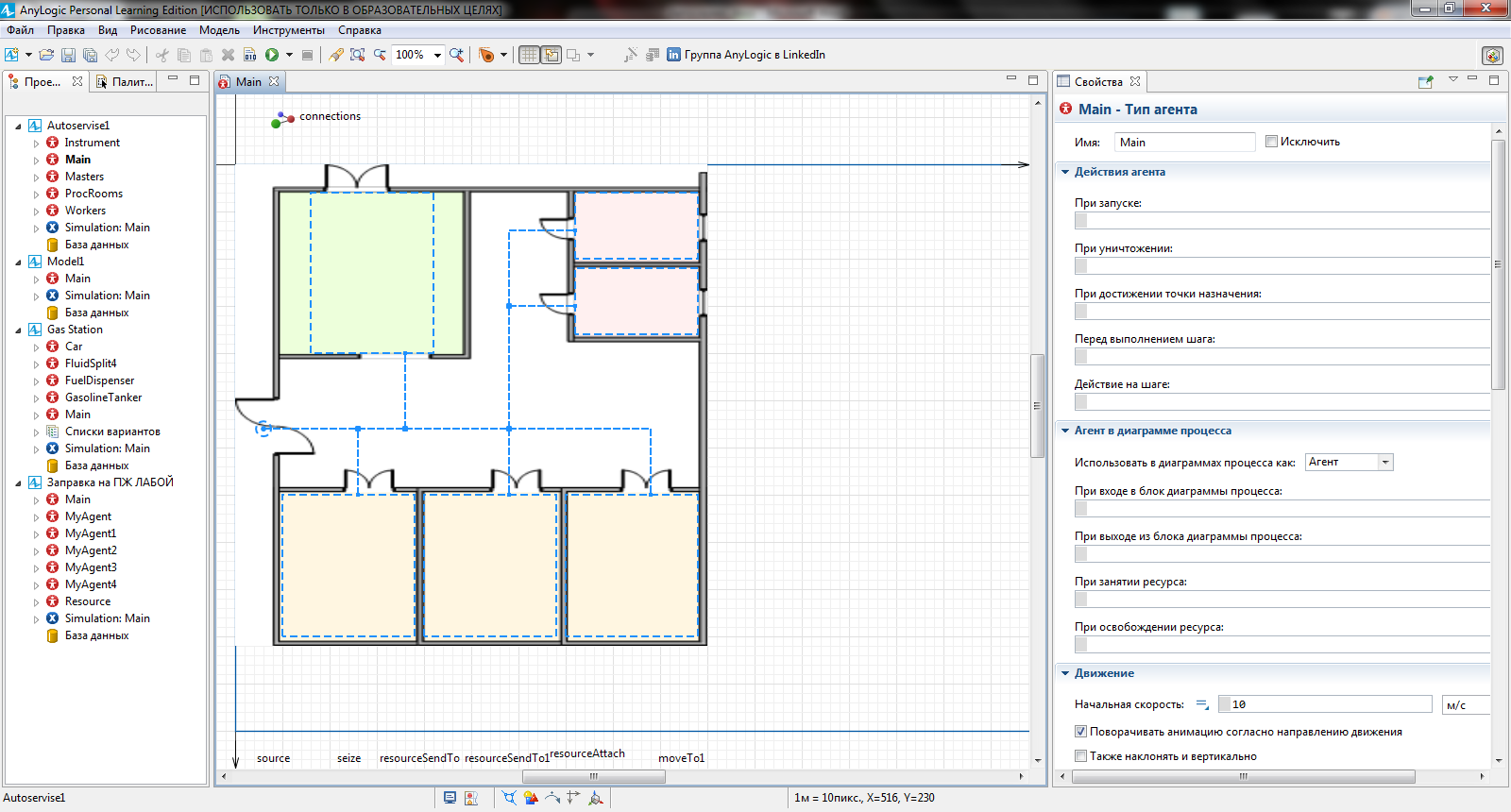
Рисунок 4.2 - Сеть, по которой будут двигаться агенты
Созданная группа обладает идентификатором network.
Проверить правильность создания группы network можно с помощью дерева проекта. Правильно созданная группа будет иметь вид, показанный на рисунке 4.4. Выделяя нужный элемент на дереве можно его удалить, или переименовать с помощью соответствующих команд контекстного меню элемента.
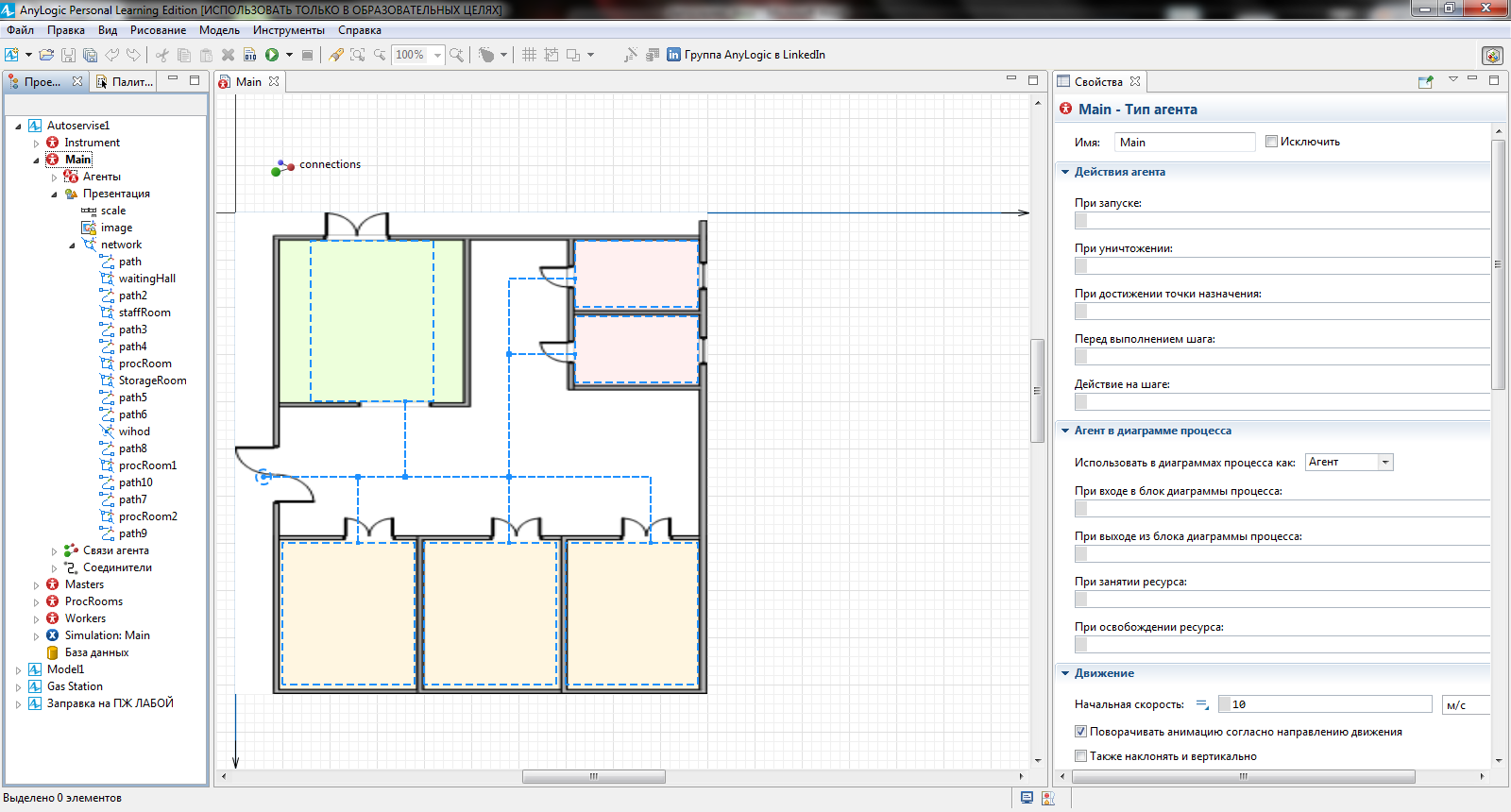
Рисунок 4.3 - Группа network на дереве проекта
Создание ресурсов модели
Следующим шагом построения модели является создание ресурсов с помощью элементов библиотеки Библиотека моделирования процессов: Тип ресурса, ResourcePool .
Перетащите на полигон вкладки Main Тип ресурса , задайте имя нового типа Instrument и выбираем визуализацию во вкладке Склады и контейнерные терминалы объект тележка, и нажимаем кнопку Готово.
Перетащите на полигон вкладки Main Тип ресурса , задайте имя нового типа ресурса Masters и выбираем визуализацию во вкладке Склады и контейнерные терминалы объект Рабочий, и нажимаем кнопку Готово.
Перетащите на полигон вкладки Main Тип агента , задайте имя нового типа Workes и выбираем визуализацию во вкладке Автодорожный транспорт объект lory 2 и нажимаем кнопку Готово.
Перетащите на диаграмму вкладки Main Тип ресурса , задайте имя нового типа ProcRooms, выберете анимация агента «нет» и нажимаем кнопку Готово.
Перейдите во вкладку Main и перетащите с Библиотеки моделирования процессов 3 объекта ResourcePool (эти элементы не будет находиться в логической модели проекта и будут располагаться ниже и отдельно не соединяясь портами с другими элементами. Они будут использоваться для описания ресурсов). Задайте свойства в этих элементах согласно следующих таблиц.
Таблица 4.1 Первый элемент.
| Свойство | Значение |
| Имя | mastera |
| Тип | Движущийся |
| Количество задано | Напрямую |
| Количество ресурсов | 5 |
| При уменьшении количества | Ресурсы сохраняются (конец смены) |
| Новый ресурс | Masters |
| Базовое местоположение (узлы) | staffRoom |
Таблица 4.2 Второй элемент.
| Свойство | Значение |
| Имя | instru |
| Тип | Переносной |
| Количество задано | Напрямую |
| Количество ресурсов | 5 |
| При уменьшении количества | Ресурсы сохраняются (конец смены) |
| Новый ресурс | Instrument |
| Базовое местоположение (узлы) | storageRoom |
Таблица 4.3 Третий элемент.
| Свойство | Значение |
| Имя | procRooms |
| Тип | Статический |
| Количество задано | Напрямую |
| Количество ресурсов | 3 |
| При уменьшении количества | Ресурсы сохраняются (конец смены) |
| Новый ресурс | procRoom |
| Базовое местоположение (узлы) | procRoom procRoom1 procRoom2 |
| Отображать анимацию по умолчанию | true |
Пешеходная библиотека
Пешеходная библиотека AnyLogic является высокоуровневой библиотекой моделирования движения пешеходов в физическом пространстве. Она позволяет моделировать здания, в которых движутся пешеходы (станции метро, стадионы, музеи), а также улицы и другие места большого скопления людей. С помощью Пешеходной библиотеки Вы можете собирать статистику, эффективно визуализировать моделируемый процесс для валидации и представления Вашей модели. Вы можете собирать статистику плотности пешеходов в различных областях модели для того, чтобы убедиться, что сервисы смогут справиться с потенциальным ростом нагрузки, вычислить время пребывания пешеходов в каких-то определенных участках модели, выявить возможные проблемы, которые могут возникнуть при перепланировке интерьера здания, и т.д. В моделях, созданных с помощью объектов Пешеходной библиотеки, пешеходы движутся в непрерывном пространстве, реагируя на различные виды препятствий в виде стен, различных областей и других пешеходов.
Модели движения пешеходов состоят из двух составляющих – среды и поведения. Под средой подразумеваются объекты физической среды - стены, различные области, сервисы, очереди и т.д. Объект среды задается специальным графическим элементом разметки, у которого задаются параметры объекта среды. Ресурсы (сервисы) также являются объектами среды. Поведение пешеходов задается блок-схемой.
Основным объектом библиотеки является пешеход. Пешеход задается с помощью объекта типа Ped. Пешеход “обитает” в заданном физическом пространстве (моделируемой среде) и передвигается согласно заданным правилам. С другой стороны, тип пешехода унаследован от типа агента Agent, поэтому пешеходы перемещаются по блок-схеме так же, как агенты.
Пешеходная библиотека совместима с Библиотекой моделирования процессов AnyLogic. Это позволяет использовать в пешеходных моделях любые объекты Библиотеки моделирования процессов, делая возможным создание сложных моделей, состоящих из блок-схем Библиотеки моделирования процессов и среды Пешеходной библиотеки. Такая совместимость возможна благодаря наличию в Пешеходной библиотеке объектов, превращающих агентов в пешеходов и наоборот.
Блок-схемы пешеходных моделей строятся с помощью объектов, содержащихся в Пешеходной библиотеке. Тип агента Ped является базовым типом для моделирования пешеходов. Как всегда, в библиотеке есть объекты для создания пешеходов и управления потоком пешеходов.
Правила задания потока пешеходов аналогичны правилам задания потока агентов в Библиотеке моделирования процессов. Разница заключается в том, что пешеходы двигаются согласно правилам движения в физическом пространстве и выбирают свой путь, анализируя текущее положение в пространстве.
Содержание
Создадим простейшую модель, моделирующую движение детей/подростков (назовем их условно пионерами) при заселении в начале смены в спортивно-оздоровительный лагерь.
Перед тем, как расселиться по комнатам, пионеры проходят медосмотр. Пионеры, прошедшие медосмотр собираются в зоне ожидания, а затем, получив приглашение, расходятся по комнатам в зависимости от номера отряда. Эта модель демонстрирует, как моделировать поток пешеходов и простейшие сервисы в Пешеходной библиотеке AnyLogic.
Модель
Создайте новую модель Пионерлагерь без использования шаблона. В свойствах модели на вкладке Основные в поле Единицы модельного времени выберите Секунды.
Анимация модели
а) Начнем с анимации модели, для того, чтобы графически задать объекты среды модели. Для этого добавим изображение плана лагеря. Мы не будем рисовать план в графическом редакторе, а просто вставим уже готовое изображение. Для этого откройте закладку Презентация панели Палитра. Перетащите элемент Изображение 
из палитры Презентация на диаграмму класса Main. Задайте свойства изображения в окне Свойства. Щелкните мышью по кнопке Добавить и выберите файл изображения плана лагеря schema.jpg. Вы увидите добавленное изображение в области предварительного просмотра в окне Свойства. Защитите изображение от редактирования, установив флажок Блокировать. Вы не сможете выбрать заблокированную фигуру в графическом редакторе до тех пор, пока Вы не снимете с нее блокировку, рисунок 5.1
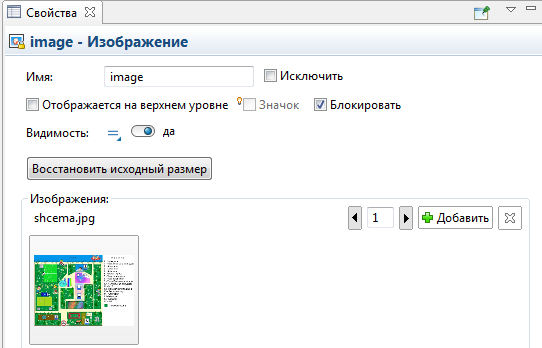
Рисунок 5.1 – окно свойств объекта Изображение
б) Теперь нужно нарисовать на анимации объекты моделируемой среды. Вначале мы нарисуем границы моделируемого нами пространства, играющую роль стен и ограждений. Выберете компонент Стена 
в палитре Пешеходная библиотека и обведите границы интересующей нас части лагеря – газоны, здания и т.д. как показано на рисунке 5.2. Эти линии будут задавать границу моделируемой среды.
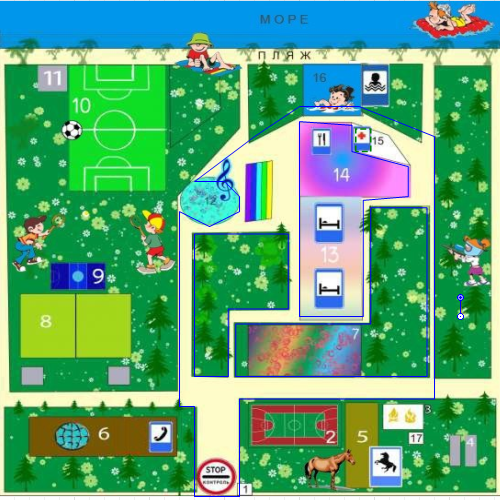
Рисунок 5.2 – границы моделируемой среды
Нарисуйте с помощью элемента Целевая линия 
вход в модель и выход из модели для пионеров, как показано на рисунке 5.3. Назовите их Вход и Вход_в_корпус соответственно. Обе линии должны находиться полностью внутри фигуры, задающей границу моделируемой среды, рисунок 5.3. После того как мы на диаграмму нарисуем первый объект разметки пространства, в структуре нашей модели автоматически появится группа графических объектов group, содержащая все элементы разметки среды (стены и целевые линии, сервисы и т.д.) и в дальнейшем в нее будут попадать все вновь вносимые элементы Разметки пространства из Пешеходной библиотеки.
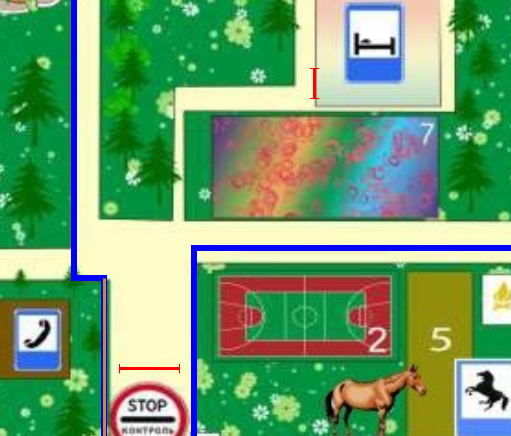
Рисунок 5.3 – расположение целевых линий Вход и Вход_в_корпус
Диаграмма процесса
Теперь создадим диаграмму моделируемого процесса движения пионеров. С помощью диаграммы процесса в моделях пешеходной динамики задается поведение пешеходов. Диаграмма процесса в AnyLogic создается путем добавления объектов библиотеки из палитры на диаграмму класса активного объекта, соединения их портов и изменения значений свойств объектов в соответствии с требованиями модели.
Попадающие в моделируемую систему пешеходы будут последовательно проходить по блокам логической схемы процесса.
Помимо объектов, составляющих логическую схему процесса, модели Пешеходной библиотеки состоят из объектов, моделирующих объекты разметки пространства (стены, различные области, сервисы, очереди и т.д.). Чтобы задать объект среды, Вы должны вначале графически нарисовать его на анимации, а затем сослаться на него в элементе логической схемы активного класса модели и задать необходимые свойства этого объекта.
Добавьте на диаграмму класса Main следующие объекты Пешеходной библиотеки:
PedSource
PedGoTo
PedSink
Разместите объекты так, как показано на рисунке 6.4, и соедините их порты.
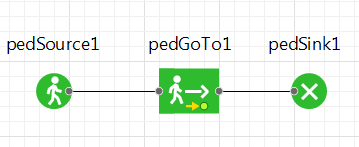
Рисунок 5.4 – объекты диаграммы процесса
Согласно принятым стандартам, блоки в логической схеме процесса обычно располагаются цепочкой слева направо, представляя собой последовательную очередность операций, которые будут производиться над пешеходом.
Теперь необходимо сконфигурировать каждый добавленный нами библиотечный объект.
Объект PedSource создает пешеходов. Обычно он используется в качестве начальной точки логического процесса, формализующей поток пешеходов. В нашем примере он моделирует приход пионеров в лагерь.
Задайте место на рисунке, где будут появляться пионеры. В свойствах компонента pedSourse выберите из списка имя Вход (имя линии, нарисованной нами для этой цели) в поле Целевая линия. Теперь наши пионеры будут появляться в случайно выбранной точке линии Вход.
Интенсивность, пешеходов в ед. времени – установите 250 т.е. пионеры будут прибывать в лагерь с интенсивностью 250 человек в час.
Поставьте галочку напротив пункта Количество прибытий ограничено, и укажите 20 в следующем пункте: Максимальное количество прибытий, т.е. прибудет 20 пионеров.
Поскольку наши пионеры – дети, скорректируем их размер, для этого в поле Диаметр, в метрах введите: uniform(0.45,0.45), а среднюю скорость их перемещения установим в поле Комфортная скорость, в м/с с помощью функции uniform(0.7,1.2).
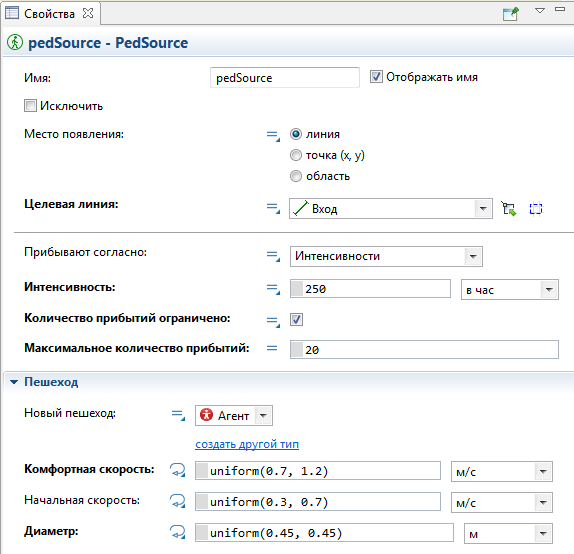
Рисунок 5.5 – окно свойств компонента pedSourse
Следующий объект в созданной нами диаграмме процесса – PedGoTo. Этот объект моделирует перемещение пешеходов из текущего местоположения в другое (заданное параметром этого объекта). С помощью этого объекта мы будем моделировать то, как пионеры перемещаются от входа в ворота лагеря к жилому корпусу.
Задайте то место, куда будут перемещаться пешеходы, достигшие этого блока в диаграмме процесса. Такое место может быть задано линией или точкой, нарисованной на презентации. На данный момент мы хотим, чтобы пионеры, вошедшие в ворота, сразу двигались к жилому корпусу. Поэтому введите Вход_в_корпус (имя линии, нарисованной нами на плане у входа в жилой корпус) в поле Целевая линия, рисунок 5.6. Теперь для того, чтобы покинуть моделируемую среду, пешеходы должны будут вначале дойти до заданной области выхода.
Оставьте заданные по умолчанию свойства объекта PedSink без изменений. Этот объект удаляет поступивших в него пешеходов из моделируемой среды. Обычно объект используется в качестве конечной точки логической диаграммы процесса.
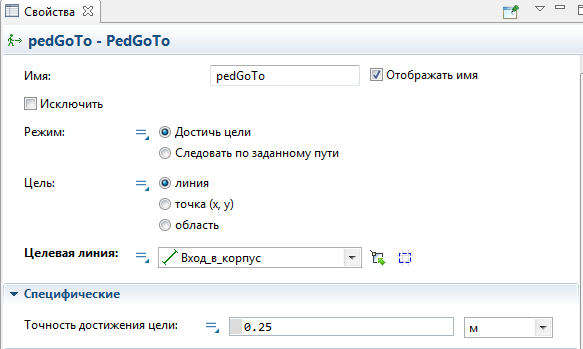
Рисунок 5.6 – окно свойств компонента pedGoTo
Выделите каждый по очереди компонент группы group и установите в окне Свойства переключатель Видимость в положение «Нет» (рисунок 5.7), чтобы не отображать на анимации фигуры, которые использовались для задания моделируемой среды (стен, различных областей, сервисов и т.д.).
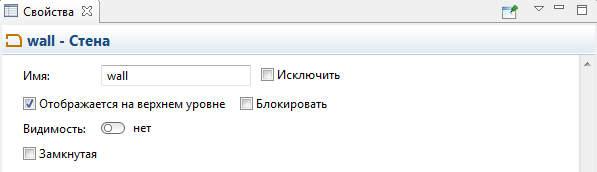
Рисунок 5.7 – свойства одного компонента wall
Запустив модель, мы увидим движение пионеров (в 2D они будут изображаться разноцветными кружками) от ворот лагеря до жилого корпуса. Одновременно можно наблюдать за перемещением агентов по логической схеме диаграммы.
Моделирование медпункта
Построив простейшую пешеходную модель детского оздоровительного лагеря, будем наполнять ее функциональностью. На данном этапе нам нужно смоделировать медпункт, через который должны пройти все пионеры, заселяющиеся в лагерь.
Вытащите компонент Сервис с очередями 
в место где изображен медпункт, сервис назовите Мед_очередь, рисунок 5.8. В окне Свойства этого компонента укажите Количество сервисов – 1, Количество очередей – 1, Тип сервиса – Точечный, рисунок 5.9.
Рисунок 5.8 – графическое изображение сервиса Мед_пункт
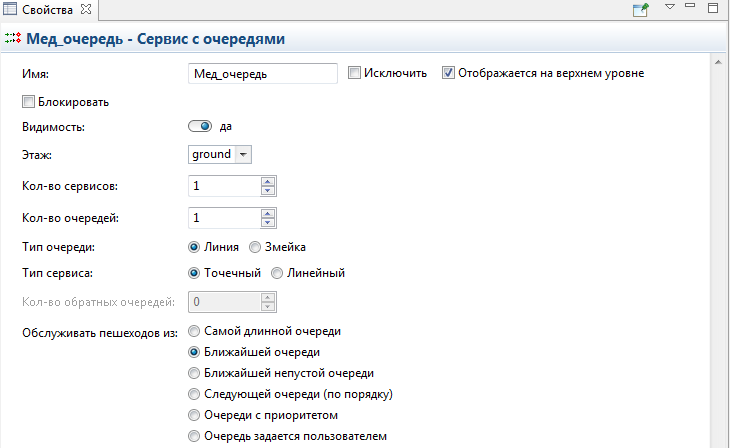
Рисунок 5.9 – параметры компонента Сервис с очередями
Теперь необходимо внести небольшие изменения в диаграмму процесса.
Добавьте в модель объект именем p edService типа PedService и соедините последний, как показано на рисунке 5.10
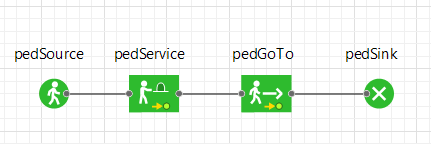
Рисунок 5.10 – диаграмма действий пешеходов
Сервис p edService задает группу одинаковых физических объектов обслуживания (например, несколько турникетов или автоматов по продаже билетов). Объект позволяет задавать очереди и сервисы в любой комбинации и задавать правила выбора сервисов – какую очередь выбрать, какой сервис выбрать, к какой очереди должен обращаться сервис, может ли сервис обслуживать несколько очередей и т.д.).
В окне свойств элемента p edService в поле Сервисы: выбереите из списка имя очереди Мед_очередь, задающего очередь, через который должны пройти пионеры (медпункт).
Укажите Время задержки: uniform(20.0, 60.0), рисунок 5.11. Это значит, что пионеры задержатся в медпункте на время от 20 до 60 секунд.
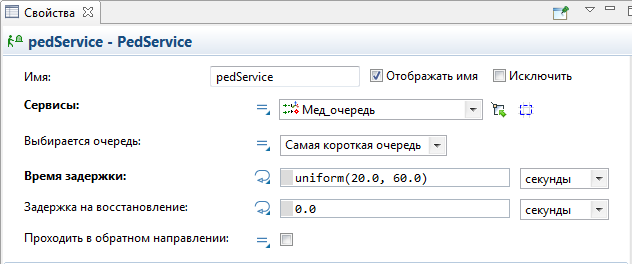
Рисунок 5.11 – настройка параметров pedService
Запустите модель и проследите за ее поведением с помощью анимации. Вы можете увидеть, что теперь пионеры проходят через медпункт, перед которым образуется очередь.
Некоторых пионеров медпункт может не допустить в лагерь, например по причине отсутствия медицинской справки. Чтобы смоделировать эту ситуацию используем объект PedSelectOutput.
Объект PedSelectOutput является блоком принятия решения Пешеходной библиотеки. Пешеход, вошедший в блок PedSelectOutput, будет перенаправляться в один из пяти выходных портов в зависимости от заданных для этих портов коэффициентов предпочтения.
Объект PedSelectOutput будет перенаправлять пионеров без медицинского допуска на выход, а пионеров с допуском – к жилому корпусу.
Добавьте на диаграмму объекты PedSelectOutput и PedGoTo, и соедините их, как показано на рис. 5.12.
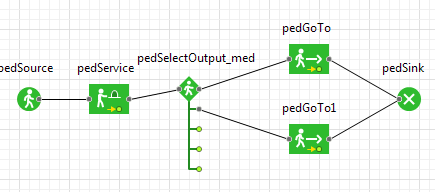
Рисунок 5.12 – логическая схема действий пешеходов
Измените свойства объекта pedSelectOutput:
• Имя: pedSelectOutput_med;
• Поставьте галочку в поле Использовать значение Вероятности;
• Коэффициенты предпочтения для пионеров, имеющих медицинский допуск (Коэфф. предпочтения 1) и не имеющих такового (Коэфф. предпочтения 2) установите 93 и 7, соответственно, рисунок 5.13. То есть, около 7% от общего числа пионеров не пройдет медосмотр.
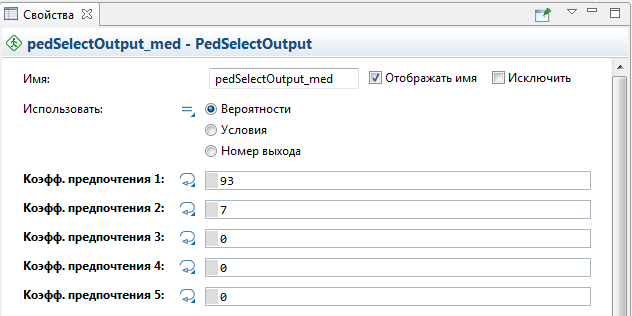
Рисунок 5.13 – окно свойств компонента pedSelectOutput
Измените свойства объектов pedGoTo и pedGoTo1:
· Имя: на_Вход и на_Выход;
· Цель (точка, линия): Вход и Вход_в_корпус.
Запустив модель, мы увидим, что некоторые пионеры не прошли медосмотр и направились к выходу.
Модельное время
В Пешеходной библиотеке, предоставляемой в версиях Anylogic PLE 7, есть ряд ограничений, среди которых ограничение на длительность эксперимента – 1 час. Для того чтобы программа не выдавала ошибку ограничим выполнение модели временем 60 минут.
В панели Проекты, выделите эксперимент Simulation: Main щелчком мыши, перейдите на страницу Модельное время панели Свойства. Здесь задаются установки модельного времени. Для того, чтобы модель останавливалась в заданное время выберите из выпадающего списка Остановить пункт В заданное время. Так как по умолчанию в качестве единиц модельного времени заданы секунды, можно просто установить конечное время 3600 единиц (секунд) в поле Конечное время.
Зададим интервал моделирования с помощью календарных дат, для этого установите флажок Использовать календарь, выберите из выпадающего списка Остановить пункт В заданную дату и установите начальную и конечную дату моделирования с помощью элементов управления Начальная дата и Конечная дата: 30.11.2015 в 10:00:00 и 30.11.2015 в 11:00:00 соответственно, рисунок 5.14.
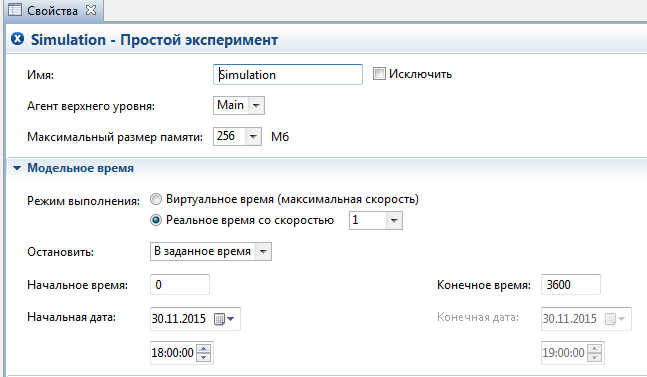
Рисунок 6.14 – модельное время
Проверьте правильность работы модели.
Персонализация пешеходов
Определим новый тип Пешехода, путем перетаскивания соответствующего элемента Пешеходной библиотеки в диаграмму класса Main. Имя пусть остается по умолчанию Pedestrian. В поле Выберите анимацию агента поставим галочку на значение нет. Заведем в нем переменную division типа Color с начальным значением
uniform() < 0.33 ? red : uniform() < 0.66 ? blue : green;.
Мы хотим, чтобы в 2D наши агенты изображались кружками трех цветов и в соответствии переменной division. Для этого на диаграмму класса Pedestrian с помощью палитры Презентация нарисуем круг с радиусом 3 и динамическим значением поля Цвет заливки равным division. А статическое значение этого поля может быть любым.
Окно класса Pedestrian должно выглядеть как на рисунке 5.15
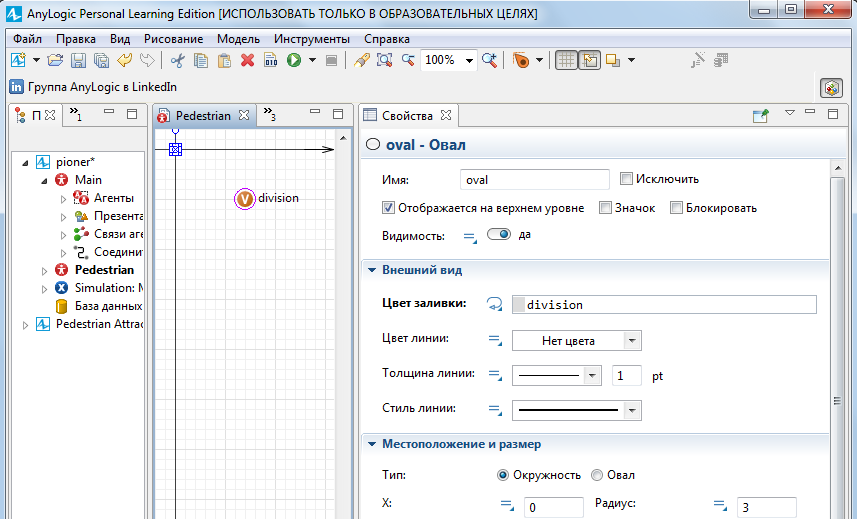
Рисунок 5.15 – Окно класса Pedestrian
Приложение А
(справочное)
Ключевые слова
| Агентное моделирование Активный объект | Объектно-ориентированный подход |
| Аналитическое моделирование | Окно свойств объектов |
| Анимация модели | Окно проекта |
| Аттракторы | Окно ошибок |
| Библиотека моделирования процессов | Окно экспериментов |
| Библиотека моделирования потоков | Оптимизация модели |
| Встроенная база данных | Палитра |
| Гибридные модели | Пешеходная библиотека |
| Детерминированные и стохастические модели | Планирование действий с помощью событий |
| Динамическое событие | Процессный подход |
| Дискретно-событийное моделирование | Подобие модели объекту |
| Задача о думающих философах | Реплицированный объект |
| Железнодорожная библиотека | Сервис с очередями |
| Имитация нескольких параллельных процессов | Система массового обслуживания |
| Интерактивный анализ модели | Справочная система документации Anylogic |
| Коллекции | Статистические модели |
| Математическая модель | Статистический таймер |
| Модель банка | Стейтчарт |
| Модель «Life» | Табличная функция |
| Моделирование динамических систем | Типы экспериментов |
| Модель Франка Баса | Целевая линия |
| Модель системной динамики | Целочисленное программирование |
| Модельное и реальное время | Эмпирическое распределение |
| Модель роста рынка | Элементы управления |
| Непрерывные модели | Язык Java |
Библиографический список
1 Доррер, Г.А. Методы и системы принятия решений: учеб. пособие/ Г.А. Доррер. – Красноярск: ИПЦ СФУ, 2013. – 180с.
2 Доррер, Г.А. Методы моделирования дискретных систем.: учеб. пособие/ Г.А. Доррер. – Красноярск: ИПЦ КГТУ, 2005. -171 с.
3 Карпов, Ю. Имитационное моделирование систем. Введение в моделирование с AnyLogic 5 [Текст] / Ю. Карпов. – СПб.: БХВ-Петербург, 2005. – 400 с.
4 Кузнецов, А.С. Теория вычислительных процессов: учеб./ А.С. Кузнецов, Р.Ю. Царев, А.Н. Князьков. – Красноярск.- Сиб. федер. ун-т, 2015.- 184 с.
5 Осоргин А.Е. AnyLogic 6. Лабораторный практикум/ А.Е.Осоргин. – Изд. 2-е, перераб. и доп. – Самара: ПГК, 2012.-110с.
6 Сьерра, К. Изучаем Java [Текст] / К. Сьерра, Б. Бэйтс; [пер. с англ.]. – М.: Эксмо, 2012. – 720 с.
7 Официальный сайт компании AnyLogic [Электронный ресурс]. – Режим доступа: www.anylogic.ru
8 Советов, Б.Я. Моделирование систем: учебник для вузов / Б.Я. Советов, С.А. Яковлев. – М.: Высшая школа, 2007. – 343 с.
Учебное издание
Александр Сергеевич Михайлов
Анатолий Анатольевич Попов
Лабораторный практикум
Ответственный редактор доц. С.А. Чичиков
Редактор РИЦ Т.А. Полуэктова
___________________________________________________________
Сдано в производство
Формат 60х84 1/16.
Усл. печ. л.
Изд. № 2/11 Тираж 150 экз. Заказ №
___________________________________________________________
Редакционно-издательский центр СибГТУ
660049, г. Красноярск, пр. Мира, 82
Факс (391) 211-97-25
Тел. (391) 227-69-90
А.С. Михайлов
А.А. Попов
МОДЕЛИРОВАНИЕ систем
Утверждено редакционно-издательским советом СибГТУ
в качестве лабораторного практикума для студентов направлений
09.03.02 «Информационные системы и технологии»
профиль подготовки «Информационные системы и технологии в промышленности»,
09.03.04 «Программная инженерия»
профиль подготовки «разработка программно-информационных систем»
очной, очно-заочной форм обучения
Красноярск 2015
Михайлов, А.С. Моделирование систем: Лабораторный практикум для студентов подготовки 09.03.02 «Информационные системы и технологии» профиль подготовки «Информационные системы и технологии в промышленности», 09.03.04 «Программная инженерия» профиль подготовки «разработка программно-информационных систем»/ А.С. Михайлов, А.А. Попов – Красноярск: СибГТУ, 2015. - 82с.
Лабораторный практикум содержит 5 лабораторных работ по основным темам курса «Моделирование систем». Тематика лабораторных работ имеет профессиональную направленность. В конце каждой лабораторной работы имеются контрольные вопросы для проверки усвоения темы.
Рецензенты:
к. т.н, доцент, СФУ А.С. Кузнецов;
д. т.н, проф., СибГТУ Г.А. Доррер.
© ФГБОУ ВО “Сибирский государственный технологический университет”, 2015
©Михайлов А.С.
©Попов А.А.
Содержание
Введение. 5
1 Основные понятия. 6
2 Основы моделирования в среде AnyLogic. 14
Лабораторная работа № 1. Моделирование упрощенного калькулятора 18
Лабораторная работа № 2. Создание модели сердца «Heart». 27
3 Создание дискретно-событийных моделей. 37
Лабораторная работа № 3. Моделирование работы светофора. 37
4 О Библиотеке Моделирования Процессов. 50
Лабораторная работа № 4 Модель работы станции автосервиса 53
5 Пешеходная библиотека. 64
Лабораторная работа № 5 Модель « Пионерлагерь». 65
Приложение А (справочное) Ключевые слова. 81
Библиографический список. 82
Введение
Практикум предназначен для изучения предмета «Моделирование систем» студентами направлений 09.03.02, 09.03.04 очной, очно-заочной форм обучения, который изучается в 4-5 семестре.
В настоящее время моделирование составляет неотъемлемую часть современной фундаментальной и прикладной науки. Поэтому при изучении данного курса представляется целесообразным использовать современные пакеты прикладных программ, предназначенные для имитационного моделирования.
Лидером среди них является отечественный продукт AnyLogic, сочетающий в себе мощный инструмент объектно-ориентированного моделирования с интерфейсом визуального программирования.
Успешное освоение лабораторного практикума способствует формированию у студента следующих профессиональных компетенций:
для направления 09.03.02
ПК-5 – способность проводить моделирование процессов и систем;
ПК-12 – способность разрабатывать средства реализации информационных технологий (методические, информационные, математические, алгоритмические, технические и программные);
ОПК-2 – способность использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования.
для направления 09.03.04
ПК–12 - способность к формализации в своей предметной области с учетом ограничений используемых методов исследования;
ПК-14 - готовность обосновывать принимаемые проектные решения, осуществлять постановку и выполнение экспериментов по проверке их корректности и эффективности.
Основные понятия
Моделирование как научный метод
Моделирование дает предположительную информацию о некоем фрагменте реальности. После определенных проверок она может оказаться истинной или ложной и потребовать построения новых моделей.
В науке, наряду с наблюдением, измерением, экспериментом и сравнением, эта процедура выступает как один из общенаучных методов. Однако моделирование можно рассматривать как особый интегрирующий метод. Его эффективность и универсализм возрастают по мере развития информационных технологий. В силу разных причин объект может быть недоступен (слишком мал или велик, далеко расположен, дорог, прекратил существование, например, в результате аварии). Исключительная польза моделирования заключается в том, что можно экспериментировать не с самой системой, а с его аналогом – моделью.
Моделирование – процесс отражения свойств одного объекта (оригинала) в другом объекте (модели). Это могут быть объекты «как есть» в целом и (или) их отдельные сущности – процессы и явления. Явления – например, поведение животного, состояния погоды – рассматриваются как сложные процессы.
В основу моделирования заложена процедура формализации – перевод свойств объекта на язык понятий предметной области, алгоритмов и математики.
Подобие модели объекту
Объект и модель находятся в отношении сходства, т.е. модель по каким-то признакам должна быть подобна изучаемому объекту. Это явление называют изоморфизмом (от греч. isos – равный и morphe – форма). Различают три вида подобия.
Первый вид подобия – подобное масштабирование. Примеры такого подобия: модели автомобилей, самолетов, кораблей сооружений и т.д.
Второй вид подобия – косвенное подобие (математическая аналогия). Удачный математический аналог из других областей знаний может сильно упростить построение модели и ее анализ. Так, очень многие физические процессы могут быть описаны уравнениями, общий вид которых q = – θ grad x (рисунок 1.1).
Перенос массы вещества – закон Фика:
j = –D · dС/dx,
где D – коэффициент диффузии; С – концентрация;
x – текущая координата.
Перенос тепла – уравнение Фурье:
q = –λ · dT/dx,
где q – тепловой поток; T – температура; λ – коэф
фициент теплопроводности.
Перенос электричества – закон Ома:
i = –c · du/dx,
где i – сила тока; c – характерная проводимость;
u – потенциал.
Рисунок 1.1 – Тройная аналогия процессов переноса
Аналогичны законы Кулона и всемирного тяготения.
Примером также может служить подобие электрических и механических явлений:
· колебание физического маятника:
· пружинного маятника;
· колебательного контура;
Третий вид подобия – условное подобие или подобие по соглашению. Примерами являются когнитивные модели (рисунок 1.2), географические карты, масштабированные чертежи сооружений, зданий, структурные схемы (модели системного анализа). При этом внешне сходство объекта и модели может не соблюдаться.
Рисунок 1.2 - Когнитивная модель потребления промышленной продукции (энергии, металлов и т.п.):
+ – положительные связи (влияния);
– – отрицательные связи (влияния).
Таким образом, объект моделирования и модель могут быть любой природы – материальными или абстрактными. Например, макет самолета – это материальная модель. Схема производства – абстрактная модель. Уравнения физики – это описание абстракций разных явлений материального мира. Модели могут быть и абстракциями других моделей. Наследование (создание одних классов на базе других) в объектно-ориентированном программировании наиболее характерный пример таких построений.
Адекватность модели
Вид и свойства будущей модели определяются целями исследователя, использующего этот инструмент. В модели отражаются свойства объекта, соответствующие этим целям, которые определяют и уровни детализации модели. В первую очередь должны быть определены существенные свойства оригинала, характеризующие его как некую проблему, которую нужно решить с помощью модели.
При этом стоит помнить, что знать все свойства предмета вашего исследования нельзя. К тому же не будем забывать, метод – это инструмент, а универсальных инструментов не бывает. Означает ли это, что моделирование – ненадежный помощник? Нет.
Во-первых, существует принцип множественности моделей. В соответствии с ним можно, а иногда – необходимо построить несколько моделей, позволяющих рассмотреть объект как проблему с различных позиций. К соответствующим решениям (моделям) можно идти, используя разные подходы. Например, создание модели поведения человека будет зависеть от разработки разных целей:
1) добиться антропоморфной кинематики компьютерной модели тела человека;
2) получить модель характерных психических реакций человека;
3) смоделировать реакции различных социальных групп людей.
Во-вторых, существуют специальные процедуры проверки, является ли модель точным представлением реальной системы, т.е., адекватна ли модель системе.
При верификации, т.е. проверке достоверности модели, определяется, правильно ли концептуальная модель (модельные допущения) преобразована в компьютерную программу.
Валидация – это процесс, позволяющий установить, является ли модель точным представлением системы для конкретных целей исследования. Определяющим моментом в этих процедурах является положение: «модель и ее результаты достоверны, если … руководители проекта признают их правильными». В итоге, если модель «адекватна», ее можно использовать для принятия решений относительно системы, которую она представляет, как если бы они принимались на основании экспериментов с реальной системой.
В-третьих, итоговый результат (т.е. «хорошая» или «плохая» модель получится) зависит от личности разработчика. Моделирование, как метод научного познания, предполагает творческий подход к объекту и целям исследования. В этом виде научного производства не обойтись без развитого воображения, умения анализировать и делать обобщения. Хорошие модели – это «минитеории» и их создание требует нестандартного мышления.
Дата: 2019-03-05, просмотров: 349.
