Рассматриваем сечение «2» с расчетными усилиями:
Расчетный изгибающий момент 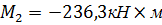
Расчетная продольная сила 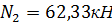
Принимаем породу древесины - сосна.
Сорт древесины - 1-ый.
Ширина досок после острожки b= 21.5см.
Расчетные сопротивления базовых пород древесины (ели, сосны по
табл. 3 СП 64.13330.2011) 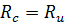 = 16МПа.
= 16МПа.
Коэффициент на породу древесины 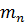 = 1,2.
= 1,2.
Коэффициент условия работы (по температурно-влажностным
условиям) 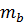 = 1.
= 1.
Расчетное сопротивление сжатию сосны 1-го сорта с учетом
коэффициентов условий работы 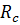 =16
=16 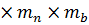 = 16
= 16  1,2
1,2  1= 19,2МПа.
1= 19,2МПа.
Расчетное сопротивление изгибу сосны 1-го сорта с учетом
коэффициентов условий работы 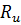 =16
=16 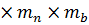 = 16
= 16  1,2
1,2  1= 19,2Мпа
1= 19,2Мпа
Требуемая высота сечения 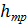 определяется приближенно по величине изгибающего момента, а наличие продольной силы учитывается коэффициентом 0.7:
определяется приближенно по величине изгибающего момента, а наличие продольной силы учитывается коэффициентом 0.7:
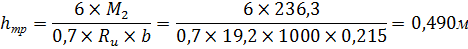
Количество слоев (досок) в сечении 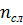 = 48
= 48
Толщина досок после острожки δ= 2см.
Принимаем высоту сечения из 30 слоев (досок): h=48*2 =96см.
Площадь сечения A=b  h= 21.5
h= 21.5  96 = 2064
96 = 2064 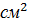
Рассчитываем высоту сечения в опорном сечении.
В опорном сечении расчетная поперечная сила Q = 34,75кН.
Расчетное сопротивление скалыванию базовой породы древесины
1-го сорта (по табл. 3 СП 64.13330.2011) без учета коэффициентов условий
работы 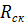 = 1,6МПа.
= 1,6МПа.
Расчетное сопротивление скалыванию сосны 1-го сорта с учетом
коэффициентов условий работы Rск=1,6 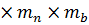 = 1,6
= 1,6  1,2
1,2  1= 1,92МПа.
1= 1,92МПа.
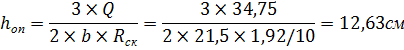
Принимаем количество досок n= 20.
Высота опорного сечения из 20 досок: 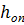 =40см.
=40см.
Площадь опорного сечения: Aоп=b 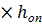 = 21,5
= 21,5  40 = 860
40 = 860 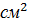
Высоту конькового сечения принимаем такой же: 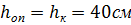
Проверка элементов рамы
Проверка напряжений при сжатии и изгибе.
Сечение 2: эксицентриситет приложения сжимающего усилия:
e= 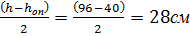
Изгибающий момент в опасном биссектрисном сечении «2»:
M= 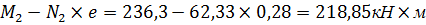
Для сжатой внутренней кромки, выполненной из клееной древесины,
расчетное сопротивление сжатию и изгибу определяется с учетом
коэффициентов 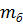 (пункт 5.2.д СП 64.13330.2011) и
(пункт 5.2.д СП 64.13330.2011) и 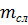 (пункт 5.2.и СП
(пункт 5.2.и СП
64.13330.2011):
Расчетное сопротивление сжатию базовых пород древесины 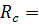 16МПа.
16МПа.
Коэффициент, учитывающий высоту сечения клееного сечения (пункт 5.2.д СП 64.13330.2011) 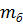 =0,86.
=0,86.
Коэффициент, учитывающий толщину отдельных слоев (досок) в
клееном сечении (пункт 5.2.и СП 64.13330.2011) 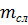 = 1,093.
= 1,093.
Коэффициент, учитывающий уровень ответственности здания γ= 1.
Расчетное сопротивление сжатию сосны 1-го сорта с учетом всех
коэффициентов условий работы
Rc=16 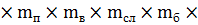 γ =
γ =
=16  1,2
1,2  1
1  1,093
1,093  0,86
0,86  1 = 18,05МПа.
1 = 18,05МПа.
Площадь сечения A=b  h= 21,5
h= 21,5  96 = 2064
96 = 2064 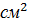
Момент сопротивления сечения:
W= 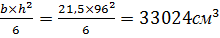
Расчётная длина:
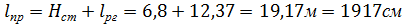
Радиус инерции сечения:
r=0,29  h= 0,29
h= 0,29  96=27,84
96=27,84
Гибкость:
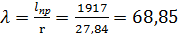 ;
;
Коэффициент, учитывающий переменность высоты сечения полурамы (табл. Е.1 СП 64.13330.2011):
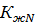 =0.07+0.93
=0.07+0.93 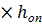 /h= 0,07+0,93
/h= 0,07+0,93  40/96= 0,457
40/96= 0,457
Коэффициент продольного изгиба:
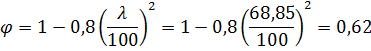
С учетом коэффициента, учитывающего переменность высоты сечения коэффициент продольного изгиба будет:
φ= 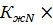 φ= 0,457
φ= 0,457 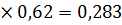
Коэффициент, учитывающий дополнительный момент от действия продольной сжимающей силы:
ξ=1-N/(φ 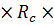 A)= 1-
A)= 1- 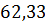 /(0,283
/(0,283  18,05
18,05  2064) =1-
2064) =1- 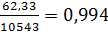
Изгибающий момент с учетом деформаций от продольной силы:
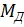 = M/ξ=
= M/ξ= 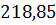 /0,994 =220,17кН
/0,994 =220,17кН 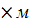
Проверка напряжений сжатия внутренней кромки карнизного узла:
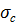 = N/A+Mд/W=
= N/A+Mд/W= 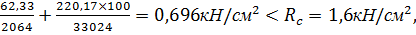 следовательно, прочность обеспечена.
следовательно, прочность обеспечена.
Расчетное сопротивление растяжению базовых пород древесины (ель, сосна по табл. 3 СП 64.13330.2011) 1-го сорта для клееных элементов 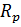 = 12МПа.
= 12МПа.
Расчетное сопротивление растяжению сосны 1-го сорта для клееных элементов с учетом коэффициентов условий работы
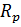 =12
=12 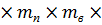 γ = 12
γ = 12  1,2
1,2  1
1  1 = 14,4МПа.
1 = 14,4МПа.
Проверка напряжений растяжения наружной кромки карнизного узла:
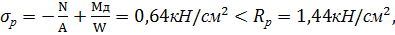 следовательно прочность обеспечена.
следовательно прочность обеспечена.
Проверка устойчивости плоской формы деформирования полурамы
Рама закреплена из плоскости по наружным кромкам с помощью стеновых панелей, панелей покрытия, поперечных сжатых связей. Внутренняя кромка не закреплена. Расчетная длина растянутой зоны равна длине полурамы, т.к. по всей длине отсутствуют сечения с нулевыми моментами: 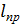 = 1917см.
= 1917см.
Площадь биссектрисного сечения: A=b  h= 21,5
h= 21,5  96 =2064
96 =2064 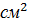
Момент сопротивления: W= 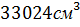
Радиус инерции из плоскости рамы:
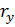 =0,29
=0,29  b= 0,29
b= 0,29  21,5 =6,235см
21,5 =6,235см
Гибкость:
λy= 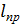 /
/ 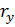 = 1317/6,235 =195,2
= 1317/6,235 =195,2
Коэффициент устойчивости при сжатии:
φy=3000/λ²= 3000/ 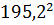 = 0,032
= 0,032
Коэффициент, зависящий от формы эпюры изгибающего момента на расчетной длине (по табл. Е.2 СП 64.13330.2011) kф= 1,13.
Коэффициент устойчивости при изгибе:
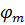 =(140
=(140 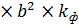 )/(
)/( 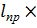 h)= (140
h)= (140 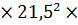 1,13)/(1917
1,13)/(1917  96) = 0,397
96) = 0,397
Коэффициенты 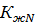 и
и 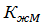 учитывают закрепление растянутой кромки из плоскости. При количестве закреплений более четырех оно считается сплошным.
учитывают закрепление растянутой кромки из плоскости. При количестве закреплений более четырех оно считается сплошным.
Угол β= 52º
Центральный угол ломаной части 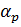 =2
=2  β= 104º.
β= 104º.
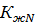 =0,75+0,06
=0,75+0,06  (
( 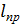 /h)²+0,6
/h)²+0,6 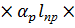 /h=
/h=
=0,75+0,06 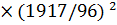 + 0,6
+ 0,6  1,815
1,815  1917/96 =46,42
1917/96 =46,42
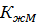 =0,142
=0,142 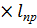 /h+1,76
/h+1,76  h/
h/ 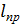 +1,4
+1,4 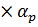 = =0,142
= =0,142  1917/96+1,76
1917/96+1,76  96/1917+1,4
96/1917+1,4  1,815 =5,46
1,815 =5,46
Проверка устойчивости полурамы:
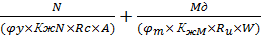 =
= 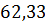 /(
/( 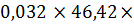 18,05/10
18,05/10 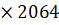 )+220,17
)+220,17  100/(
100/( 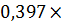 5,46
5,46  18,05/1 0
18,05/1 0 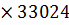 ) = 0,182
) = 0,182 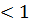
Условие выполняется, следовательно устойчивость полурамы обеспечена.
Расчёт узлов
Опорный узел
Усилия, действующие в узле: 
Расчетная продольная сила в сечении «1» N=56,76кН.
Расчетная поперечная сила в сечении «1» Q= 34,75кН.
Материал – сосна 1-го сорта.
Ширина сечения b = 21.5см.
Проверка прочности на смятие торца стойки.
Высота сечения: 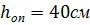
Площадь сечения:F=b 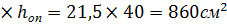
Расчётное сопротивление смятию: 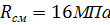
Коэффициент 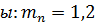 ;
; 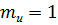 ;
; 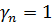 .
.
Расчётное сопротивление смятию с учётом коэффициентов:
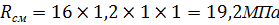
Напряжение смятия:
σ= 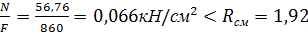 – условие выполняется.
– условие выполняется.
Проверка напряжения смятия поперек волокон по площади примыкания стойки к упорной вертикальной диафрагме
Расчётное сопротивление смятию поперек волокон 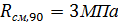
Расчётное сопротивление смятию поперек волокон с учётом коэффициентов:
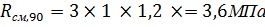
Требуемая высота диафрагмы:
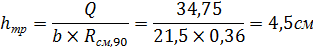
Принимаем 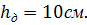
Площадь смятия стойки: 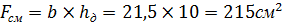
Напряжения смятия поперек волокон по площади примыкания стойки к упорной вертикальной диафрагме:
σ= 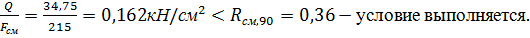
Рассчитываем упорную вертикальную диафрагму на изгиб как балку пролетом b, частично защемлённую на опорах, с учётом пластического перераспределения моментов.
Изгибающий момент:
M= 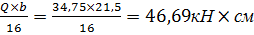
Расчётное сопротивление стали класса С245 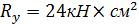
Требуемый момент сопротивления:
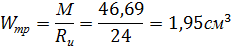
Этому моменту сопротивления должен быть равен момент сопротивления сечения упорной диафрагмы определяемый по формуле:
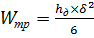 ,
,
тогда толщина диафрагмы:
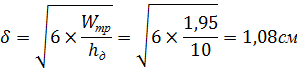
Принимаем 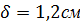
Боковые пластины принимаем той же толщины. Площадь 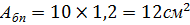
Момент сопротивления W= 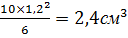
N= 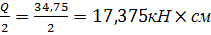
σ= 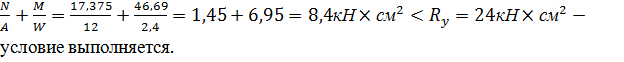
Башмак крепим к фундаменту двумя анкерными болтами, работающими на срез и растяжение. Сжимающее усилие передаем непосредственно на фундамент.
Изгибающий момент, передаваемый от башмака на опорный лист:
М= 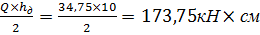
Длина опорной плоскости башмака l=32,5см.
Ширина свеса опорной плоскости башмака b=9,3см.
W= 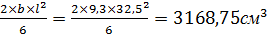
Сминающие напряжения под башмаком:
σ= 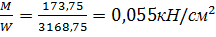
Материал фундамента – бетон класса В10, с призменной прочностью 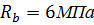 .
.
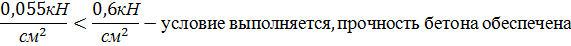
Анкерные болты принимаем из стали 09Г2С диаметром 22мм.
Площадь болта брутто 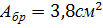
Площадь болта нетто 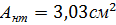
Для того, чтобы срез воспринимался полным сечением болта, устанавливаем под гайками шайбы толщиной 10мм. Усилия в болтах:
Растягивающее усилие:
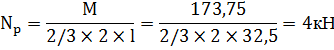
Срезающее усилие:
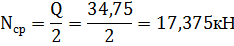
Напряжения растяжения в сечении болта ослабленного резьбой:(в переделах нарезки резьбы)
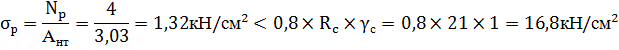
Коэффициент условия работы γс= 1.
Коэффициент учитывающий неравномерную работу болтов – 0,8.
Напряжения среза:
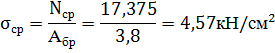
Расчётное сопротивление болта срезу 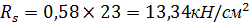
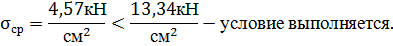
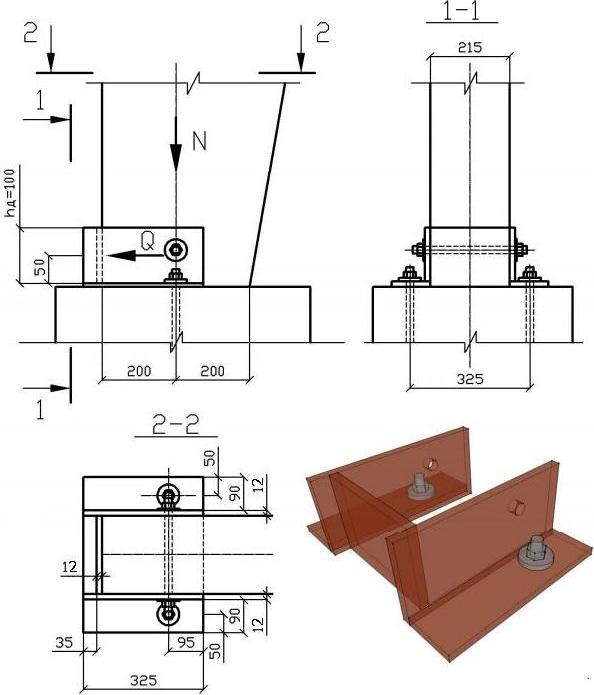
Рисунок 5 – Опорный узел
Коньковый узел
Коньковый узел выполняется с использованием деревянных накладок и болтов. На накладки действует поперечная сила от односторонней нагрузки.
Поперечная сила от односторонней снеговой нагрузки 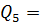 33,96кН.
33,96кН.
Толщина накладки а=12,5см
Высота сечения 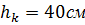
Материал - сосна 1-ого сорта
Коэффициент 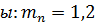 ;
; 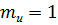
Толщина слоя(доски) клееного сечения 2см.
Коэффициент, учитывающий толщину слоев для клееных элементов 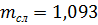 .
.
Коэффициент, учитывающий толщину слоев для клееных элементов 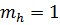 .
.
Усилие, передающееся на первый, ближайший к коньку ряд болтов:
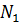 =
= 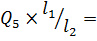 33,96
33,96 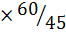 =41,38кН,где
=41,38кН,где
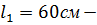 расстояние от конька до второго ряда болтов
расстояние от конька до второго ряда болтов
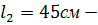 расстояние между болтами
расстояние между болтами
Усилие, передающееся на второй ряд болтов:
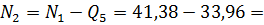 7,42кН
7,42кН
Принимаем болты диаметром 24мм.
Несущая способность в одном срезе болта при изгибе:
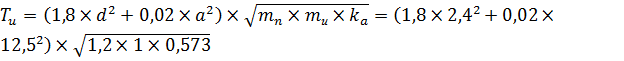 =11,118кН,
=11,118кН,
но не более
2,5 
Угол наклона ригеля 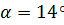 ; 90
; 90 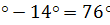
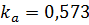 (по табл.21. СП 64.13330.2011)
(по табл.21. СП 64.13330.2011)
При смятии древесины:
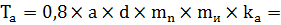
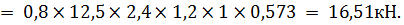
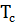 =0,8
=0,8  b
b 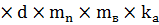 =
=
=0,8  21,5
21,5  2,4
2,4  1,2
1,2  1
1  0,573 = 28,38кН.
0,573 = 28,38кН.
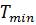 = 11,118кН.
= 11,118кН.
Число срезов болтов в первом ряду nср= 2.
Число двухсрезных болтов в первом ряду
n1=N1/(Tmin  nср)= 41,38/(11,118
nср)= 41,38/(11,118  2) = 1,86
2) = 1,86
Принимаем n1= 2 болта.
Во втором ряду
n2=N2/(Tmin  nср)= 7,42/(11,118
nср)= 7,42/(11,118  2) = 0,334.
2) = 0,334.
Принимаем n2=1 болт.
Смятие торцов полурамы под углом α=14° к продольным волокнам:
Σ = N/(b  hоп) = 34,75/(21,5
hоп) = 34,75/(21,5  40) = 0,04кН/см2 .
40) = 0,04кН/см2 .
Rсм/(1+(Rсм/Rсм90-1)  sin³α) = 16/(1+(16/3-1)
sin³α) = 16/(1+(16/3-1)  sin314) = 14,37МПа.
sin314) = 14,37МПа.
Проверяем накладки на изгиб
M=Q  (l1-l2)= 33,96
(l1-l2)= 33,96  (60-45) =509,4кН
(60-45) =509,4кН  см
см
Высота накладки hн= 30см.
Момент сопротивления накладки
Wнт=2  ан
ан  h2н/6= 2
h2н/6= 2  12,5
12,5  302 /6 = 3750см3 .
302 /6 = 3750см3 .
Напряжение в накладке
σ=M/Wнт= 509,4/3750 = 0,136кН/см2 .
Расчетное сопротивление древесины накладки на изгиб Rи= 14МПа.
Расчетное сопротивление древесины накладки на изгиб с учетом коэффициентов
Rи  mп
mп  mв= 14
mв= 14  1,2
1,2  1 = 16,8МПа.
1 = 16,8МПа.
Так как напряжение в накладке
σ= 0,136кН/см2 < 1,68кН/см2 = Rи  mп
mп  mв, следовательно прочность обеспечена.
mв, следовательно прочность обеспечена.
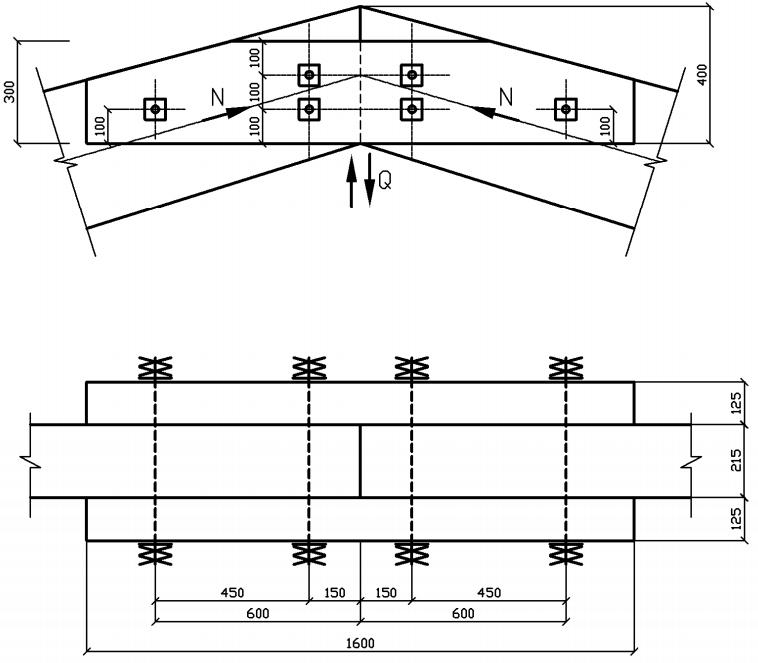
Рисунок 6 – Коньковый узел
Заключение
В ходе курсового проекта я ознакомился с расчётом деревянных конструкций и научился рассчитывать кровельные ограждающие конструкции, рабочий настил, прогоны, клеефанерную панель покрытия, а также трехшарнирную раму из клееной древесины.
Список литературы
1 СП 20.13330.2016 «Нагрузки и воздействия». Актуализированная редакция СНиП 2.01.07- 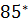 – М.;Минрегион России,2016;
– М.;Минрегион России,2016;
2 СП 64.13330.2011 «Деревянные конструкции». Актуализированная редакция СНиП ӀӀ-25-80– М.;Минрегион России,2011;
2 Дымолазов М.А «Деревянные конструкции. Клееные трёхшарнирные рамы. Конструирование и расчёт» - Казань: Изд-во Казанск. гос. архитект.-строит. ун-та, 2016 г, 89 с.
3 Гринь И.М «Строительные конструкции из дерева и синтетических материалов», 1975 г, 233 с.
Дата: 2019-03-05, просмотров: 417.