Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Под временем эффективной влагозащиты элемента РЭС понимают то время, в течение которого через защитную оболочку из полимерного материала пройдет критическое для данной изоляции количество влаги. Величина критического количества влаги q_кр определяется объемом изоляции V_из, коэффициентом растворимости влаги в изоляции h_из и величиной критической влажности N_кр.

 

Q_кр=V_изh_изN_кр.                                              (70)

 

Самое сложное в данном расчете - это определить N_кр. Зная N_кр, можно рассчитать срок эффективной защиты от влаги элемента РЭС в оболочке из полимерного материала.

Для определения величины N_кр представим элементы РЭС в виде физической модели, объясняющей поведение элемента в условиях повышенной влажности окружающей среды

(рис. 18 ) 1 – элемент; 2 - оболочка из полимера; 3 - электрический вывод; 4 - дефект в оболочке; I - поток влаги через оболочку; II - поток влаги в месте вывода; III - поток влаги через дефект в оболочке I, II, III - возможные пути проникновения влаги).

 

 

Рис. 18

 

По воздействию пара (воды) на функциональное ядро элемента, микромодуля или ИС все элементы разделяют на три типа.

1. Элементы, у которых внутренний объем заполнен газом, т.е. гидроизоляция не контактирует с поверхностью функционального узла.

2. Элементы, внутренний объем которых заполнен электроизолирующей жидкостью, т.е. непосредственного контакта нет.

3. Элементы, у которых есть хороший непосредственный контакт герметика с функциональным узлом.

 

В первом случае диффузия влаги приводит к увеличению влажности во внутреннем объеме с адсорбцией влаги.

Во втором случае возможно образование раствора или эмульсии. В случае помещения элемента в условия повышенной влажности проникновение влаги в диэлектрик может подчиняться тем же закономерностям. Влага будет проникать к функциональному ядру через дефектную часть оболочки. Если предположить, что:

а) диэлектрик оболочки изотропен;

б) скорость адсорбции со стороны окружающей среды выше скорости диффузии в оболочке;

в) коэффициент диффузии не зависит от концентрации влаги;

г) температура в процессе диффузии постоянна, тогда скорость диффузии через герметизирующую оболочку подчиняется эмпирическому уравнению

 

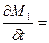Ð 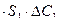,                                                 (71)

 

где M₁ - масса продифундировавшей влаги за время t; D₁ - коэффициент диффузии через материал оболочки; S₁ - площадь бездефектной оболочки; C₁ - концентрация влаги.

Скорость проникновения влаги через неплотные соединения (II) можно определить по эмпирическому уравнению

 

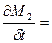Ð_S 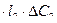,                                   (72)

 

где M₂ - масса влаги, прошедшей через поверхность раздела за время t; Ð_s - коэффициент поверхностной диффузии вдоль поверхности раздела герметик – токовывод; l₂ - периметр электрического вывода; DС₂ - градиент концентрации влаги вдоль вывода.

Если считать, что элементы проходят контроль после изготовления и не могут иметь дефектных мест в оболочке, можно исключить случай проникновения влаги по дефектам и записать, что количество влаги, проникающей через функциональный элемент, равно

 

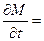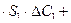Ð₁ Ð 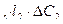.                                      (73)

 

Последнее выражение можно считать математической моделью поведения радиодетали во влажной среде, так как с количеством проникающей влаги коррелируются все параметры функционального ядра.

При расчете времени эффективной влагозащиты изделия следует дифференцируемо рассматривать два случая:

1. Защита невлагоёмкого изделия.

2. Защита изделия, имеющего влагоёмкие элементы (например, бумага).

Дело в том, что водяные пары, проникающие под оболочку невлагоёмкого изделия, целиком идут на увеличение парциального давления в замкнутом объеме между оболочкой и невлагоёмким изделием. При наличии влагоемкой составляющей водяные пары в первый момент времени поглощаются этой составляющей и до определенного момента не вызывают ухудшения электрических характеристик элемента.

 

Вопросы для самоконтроля

 

1. Назовите основные стадии процесса влагообмена.

2. В чём заключается сущность первого и второго законов Фика?

3. Что понимают под временем эффективной влагозащиты элемента РЭС?

4. Расскажите методику расчёта влагозащиты?

5. На какие три типа делятся элементы в зависимости от воздействия воды на функциональное ядро элемента?

6. Какие два случая следует рассматривать при расчёте времени эффективной влагозащиты?

 

Лекция №8. Способы влагозащиты полимерными материалами

Известные способы защиты от влаги можно классифицировать в зависимости от условий.

Так, например, по условиям работы изделия подразделяют на четыре основные группы.

Защита от внешнего воздействия окружающей среды при малом уровне относительной влажности (не превышающей 65-75 %), небольших колебаниях температуры (от -20 до +40 °С) и кратковременных механических воздействиях. Защита от повышенной влажности (95-98 %) при температуре от -40 до +50 °С и внешних механических воздействиях при эксплуатации в полевых условиях на подвижных объектах.

Защита от повышенной (95-98 %) влажности и одновременного действия перепадов температуры (от -60 до +100 °С) при повышенных внешних механических воздействиях в период эксплуатации на кораблях, самолетах.

Защита от повышенной (95-98%) влажности при обильной ее конденсации, при одновременном циклическом действии больших перепадов температур (от -60 до +100 °С) при повышенных механических воздействиях.

 

8.1. Герметизация. Способы герметизации

 

Предотвратить действие большинства упомянутых дестабилизирующих факторов помогает прием выполнения РЭС, называемый герметизацией.

Она бывает:

q пылезащитной;

q водозащитной;

q влагозащитной;

q вакуум-плотной.

Пылезащитная герметизация предназначена для защиты узлов, блоков и аппаратов от проникновения в них пыли. Для защиты от проникающей способности мелкодисперсной пыли достаточно большие швы защищаемой конструкции должны быть очень плотными.

Водозащитная герметизация предохраняет аппараты от попадания воды, находящейся под небольшим давлением.

Влагозащитная герметизация предохраняет радиоаппаратуру от попадания влажного воздуха.

Вакуум-плотная герметизация предполагает хорошую защиту не только от влажного воздуха, но и от агрессивных (сухих) газов. Такая защита является наиболее сложной и дорогой.

Герметизация может быть обеспечена одним из следующих способов:

· защитой изделия от влаги с помощью изоляционных материалов;

· защитой изделия с помощью непроницаемых для газов и влаги оболочек (герметичных корпусов).

 

Вопросы для самоконтроля

 

1. По каким условиям работы можно классифицировать способы влагозащиты?

2. Что называется герметизацией? Виды герметизации?

3. Какие способы герметизации существуют?

 

Лекция №9. Нестационарный тепловой режим

простейших моделей РЭС

 

Если температурное поле меняется во времени, т.е. является функцией времени, то протекающие в таких условиях тепловые процессы называются нестационарными. Нестационарность тепловых процессов обусловливается изменением энтальпии тела, т.е. его теплосодержанием, в конечном счете, нестационарность тепловых процессов связана с явлением прогрева (охлаждения) тела.

Пусть тело внесено в среду с более высокой температурой. Сразу же между телом и средой возникает процесс теплообмена, и тело начинает нагреваться (рис.19).

 

Рис. 19

 

Сначала нагреваются поверхностные слои (t_n), но постепенно процесс нагрева распространяется и в глубь тела (t₀). Если рассматривать зависимость температуры от времени, то видно, что температура поверхности и температура в центре тела достигает температуры среды по прошествии длительного времени, а сам ход процесса следует сложной зависимости и может быть представлен экспериментальным законом (рис. 19).

 

                                    Ф  

 

 

tК

t

                 

 

Рис. 20

 

При нестационарном режиме интенсивность подвода тепла в системе среда - тело тоже непостоянна во времени. О характере изменения этой величины можно судить по рис. 20.

Из рисунка видно, что по мере прогрева тела интенсивность передачи теплоты постоянно уменьшается и в пределе становится равной 0. Площадь, заключенная между осями и кривой, определяет полное количество теплоты, переданное за время нагревания тела. Эта теплота аккумулируется телом и идёт на повышение его энтальпии. Аналогичным образом протекает процесс охлаждения тела. При этом его энтальпия уменьшается, а выделенная теплота передается в окружающую среду. Скорость изменения энтальпии прямо пропорциональна способности материала проводить теплоту и обратно пропорциональна его способности удерживать теплоту (аккумулирующие способности). Поэтому в целом скорость теплового процесса при нестационарном режиме определяется значением коэффициента температуропроводности

 

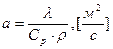.                                                    (74)

 

Подобный характер зависимости температуры от времени справедлив лишь для твердых тел. При нагреве жидких или газообразных тел сразу возникает конвекция, которая способствует выравниванию температур. В этом случае говорят лишь о средней температуре. Решить задачу нестационарной теплопроводности - это значит найти зависимость изменения температуры и количества переданной теплоты во времени для любой точки тела. Такие зависимости могут быть получены путем решения дифференциального уравнения теплопроводности.

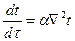.                                                 (75)

 

Аналитическая теория ставит своей целью получение общего решения. Такие решения получаются достаточно сложными даже для тел простой формы.

Любой процесс нагревания или охлаждения можно разделить на три режима.

1. Начало - его характерной особенностью является распространение температурных возмущений во всех направлениях и с разной скоростью и захват всё новых и новых слоев тела. Скорость изменения температуры в разных точках различна. Поле температур сильно зависит от начального состояния, и поэтому первый режим характеризует начальную стадию развития процесса.

2. С течением времени влияние начальных неравновесностей сглаживается и относительная скорость изменения температуры во всех точках тела становится постоянной. Это режим упорядоченного процесса. Он подчиняется простому экспоненциальному закону и носит название регулярного режима.

3. Наступает по прошествии длительного времени. Он характеризуется постоянством температуры во времени и носит название стационарного теплового режима.

Наиболее часто задача о нестационарном поле РЭС может быть сформулирована следующим образом:

1. В некоторый момент времени РЭС подключили к системе электропитания. Под влиянием источников тепла температурное поле меняется во времени. Требуется определить степень перегрева различных точек в различные моменты времени

 

 

Рис. 21: 1 - функциональное ядро; 2 – зазор; 3 - корпус

2. Нестационарный тепловой режим аппарата при подаче энергии периодическим импульсом представлен на рис. 22.

 

 

 

 

-------- среднее значение

_____ на самом деле

Рис. 22

 

В этом случае зависимость перегрева от времени носит периодический характер. Колебание температуры происходит около некоторого среднего значения, которое тоже изменяется во времени.

3. Тепловой режим РЭС изменяется вследствие изменения во времени температуры среды окружающей аппарат. Во всех этих случаях на практике пользуются приближёнными методами анализа.

 

9.1.Приближенные расчеты нестационарных

температурных полей

 

Эти расчеты базируются на теории регулярного теплового режима, созданной академиком Кондратьевым, главное положение в которой формулируется так: температурное поле тела или системы тел входит в стадию регулярного режима с самого начала рассматриваемого процесса.

Одной из важных характеристик системы является тепловая инерция. Её характеризует время t_1,2, в течение которого температура перегрева изменяется от V₁ до V₂.

 

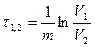,                                                        (76)

 

где m – темп нагревания (охлаждения) системы.

На протяжении этой стадии m остаётся неизменным для данного тела и не зависит от времени и выбора точек внутри тел.

m занимает центральное место в теории регулярного режима. На протяжении этой стадии m остается неизменным для данного тела и не зависит от времени и выбора точек внутри тела.

Практически m можно определить из соотношения

 

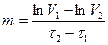.                                         (77)

 

Здесь V₁ > V₂  и t₂>t₁, V₁=t₁-t₂ и V₂=t₂-t₁.

Для определения t_1,2  следует задать величину абсолютного значения разности

V₂ = t₂-t_c.                                                      (78)

 

Эта величина должна лежать за пределами требуемой точности расчета температур.

Например:

1) Блок, имеющий начальную температуру t₁, помещен в среду с иной температурой (t_c ¹ t₁). Тогда время t_1,2, необходимое для достижения температуры t₂, определяется по формуле

 

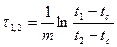.                                      (79)

2) Блок до стационарной температуры (V_jCТ) в некоторой     точке разогревается под влиянием источников энергии от температуры V_j. Найти время t достижения требуемой величины Dj=( V_jCТ)-V_j.

 

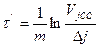.                                           (80)

 

Поскольку V_jCТ есть не что иное как t^`_i – t_j, то пользуясь выражением (14), можно записать:

 

V_jСТ=Ф×R_j, или V_jСТ= 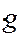Ф_iR_ij,                    (81)

 

i,j – характеристики изотермической поверхности.

Вид теплового коэффициента R для разных случаев теплообмена и тел разной конфигурации мы уже рассмотрели.

Рассчитаем нестационарное температурное поле системы с источником энергии.

А) Рассмотрим систему тел с источниками энергии, общая мощность которых Ф, достигается после их включения.

Темп регулярного режима m. Рассмотрение проведем в точке j и будем считать, что известны начальный (V_j0) и установившийся перегревы [(V_j)_СТ] в этой точке. Стационарную температуру будем характеризовать с помощью теплового коэффициента R_j; тогда можно воспользоваться (81). Пусть регуляризация температурного поля в точке j наступает с начального момента времени t = 0. Требуется определить нестационарное температурное поле в точке j. Для этого необходимо воспользоваться еще одним положением теории регулярного теплового режима, согласно которому температура V_j в любой точке тела j с источниками энергии связана с помощью источников Ф соотношением

 

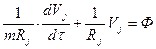.                                         (82)

 

Пусть V_j-(V_j)_СТ=Е_j, а V_j=E_j+(V_j)_CT.

Тогда из (81) и (82), разделив на Ф правую и левую части получившегося уравнения, имеем

 

а)                                   ;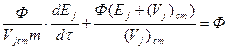

б)                                  ;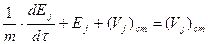

в)                                                                                                             (83)

 

После интегрирования (83) получаем

 

V_j-(V_j)_СТ=A₁×e^-mt                                              (84)

 

где А₁ – постоянная интегрирования, ее можно определить из начального условия

A₁=[Vj-(V_j)_СТ]_t=0= Vj₀-(V_j)_СТ.                     (85)

 

Подставив (85) в (84) можно, записать

 

Vj-(V_j)_СТ=[Vj₀-(V_j)_СТ] ×e^-mt ,                        (86)

или

V_j=V_j0×e^-mt +(V_j)_СТ×(1- e^-mt) .                    (87)

 

Если начальное поле температур равномерно и температура тела равна температуре

среды, то V_j0=0, а (87) принимает вид

 

V_j=(V_j)_СТ×(1- e^-mt),                                       (88)

или, учитывая (81):

V_j=R_j×Ф× (1- e^-mt),                                             (89)

т.е. задача сводится к определению теплового коэффициента R_j и темпа охлаждения системы (изменения m) в среде с постоянной температурой.

Б) Предположим теперь, что в момент времени t₁ источники энергии отключены и система тел начинает охлаждаться в среде с той же температурой t_c. К этому времени t₁ перегрев в точке j согласно (88)

 

V_j1=(V_j)_СТ×(1- e^-mt1).                                     (90)

 

Он сразу же начнет изменяться. Допустим, это изменение будет происходить по экспоненциальному закону (т.е. сразу же наступает регулярный режим), тогда перегрев V_j2 в момент времени t₂³t₁

 

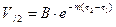.                                       (91)

 

В – постоянная интегрирования - может быть определена из (89) при условии

V_j2=V_j1.                                                                  (92)

Тогда t₂=t₁.

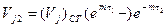.                          (93)

 

Таким образом, мы провели расчет изменения во времени температуры системы при включении и выключении источников энергии.

Следует иметь в виду, что предложенный метод расчета является приближенным. Степень приближения зависит от многих факторов (стационарного и начального полей, условия охлаждения и др.).

Графический характер зависимости V=f(t) для выражений (90) и (93) приведен на рис. 23.

 

 

Рис. 23

 

Вопросы для самоконтроля

 

1. Какой тепловой режим называется нестационарным?

2. Что значит решить задачу нестационарной теплопроводности?

3. На какие три режима можно разделить процесс нагревания или охлаждения?

4. Каким образом могут быть сформулированы задачи о нестационарном поле РЭС?

5. На какой теории базируются расчёты нестационарных температурных полей?

 

 

Лекция №10. Стационарный тепловой режим

 простейших моделей РЭС

Сложности, возникающие при решении задач, связанных с нестационарным ходом процесса, вынуждают полагать процесс стационарным (не изменяющимся во времени), однако и в этом случае есть свои сложности.

РЭС представляет собой систему многих тел с внутренними источниками тепла, которые формируют температурное поле аппарата. Его вид зависит от мощности и распределения источников тепла, конструкции и режимов работы аппарата, систем охлаждения, геометрических параметров, физических свойств материала, условий эксплуатации и т.д.

При изучении стационарного режима РЭС задача формулируется следующим образом: надо найти температуру t_j области j в зависимости от суммарной мощности источников Ф:

 

t_j=f(Ф).                                        (94)

 

Эта температура является аддитивной функцией температуры среды (t_c) и температуры перегрева V_j, возникающего в результате действия всех источников тепла в аппарате. Влияние источников тепла на тепловой режим области j будет выражаться формулой

 

V_j=t_i-t_c=V_j(Ф).                              (95)

 

Зависимость температуры перегрева V_j от суммарной мощности Ф всех источников, действующих в аппарате, называется тепловой характеристикой j-й области аппарата. Совокупность таких областей образует систему многих тел с сосредоточенными источниками тепловой энергии. Анализ температурных полей таких систем является сложной задачей. Для её решения всё многообразие конструкций РЭС подразделяется на две группы.

Характерной особенностью модели является разделение всех поверхностей модели на отдельные условно изометрические участки. Например, при определении среднеповерхностной температуры условной зоны условно-изотермическими считаются такие участки, как поверхность корпуса, вся поверхность нагретой зоны, состоящей из поверхностей элементов и части шасси, не занятой им.

 

 

 

 

Рис. 24

На рис. 24,а, показан разрез РЭС и значения температур, измеренных в разных точках корпуса, шасси и элементной базы.

На рис. 24,б представлена тепловая модель аппарата, на основании которой определяются среднеповерхностные температуры, при этом сложный по форме контур заменен на прямоугольник, поверхность которого изотермическая. Такое допущение применяется к корпусу. Задача упрощается настолько, что математическое описание теплообмена становится возможным и сравнительно несложным.

Вторая группа: нагретая зона РЭС представляет собой неоднородную систему многих тел, представленных в виде однородного тела, свойства этого тела характеризуются эффективными значениями коэффициента теплопроводности и теплоёмкости. Внутри этого анизотропного тела по объему распределены источники энергии. Совокупность таких тел образует систему тел. Рассмотрим систему тел с источниками тепла, в которых происходит теплообмен между ними, а также и с окружающей средой. Допустим, что эта система тел омывается жидкостью или газом (рис. 25 где t_l>t₂>t₃>t_c; t_l, t₂, t₃ -среднеповерхностные температуры тел).

 

 

 

Рис. 25

 

Рис. 25

В соответствии с законом сохранения энергии можно записать систему

Ф₁=Ф_1с+Ф₁₂+Ф₁₃ ;

Ф₁₂=Ф_2с+Ф₂₃;                                            (96)

Ф_3с=Ф₂₃+Ф₁₃.

 

Фij - тепловой поток от i-го тела к j-му.

Тепловые потоки можно выразить через температурные (t_i-t_j) напоры и тепловые проводимости s_ij:

 

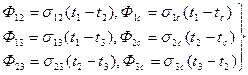.                              (97)

 

Подставим (97) в (96).

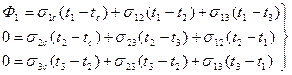.                   (98)

 

Для системы из N тел

 

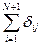(t_j -t_i) = Ф_j,                                                          (99)

 

где d_ij - тепловая проводимость от i-го тела к j-му; t_i,t_j – температуры тел i и j.

Особенности экспериментального исследования тепловых режимов и, в частности замер температуры с помощью термопар, предполагают измерения не температуры тела (среды), а температуры перегрева тела над средой V_j = t_j – t_c.

Перепишем выражение (97):

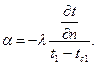                                      (100)

 

Из сравнения систем (100) и (97) видно, что последняя проще. Ее также можно представить в общем виде:

 

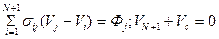.                                    (101)

Это уравнение теплового баланса системы тел.

 

10.1. Принцип суперпозиции

 

Если мощность источников тепла, коэффициенты теплопроводности отдельных частей системы и коэффициенты теплообмена не зависят от температуры, то в точке j системы стационарная температура зависит от мощности источников.

 

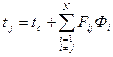,                                      (102)

 

где t_c - температура внешней среды; F_ij - тепловые коэффициенты; N - число областей системы; Ф_i - мощности источников в i-ой части системы.

Записанное уравнение является принципом суперпозиции, который гласит, что температура i-го элемента равна сумме температуры t_c среды и алгебраических сумм перегревов, возникающих за счет действия всех источников тепла. В этом случае исследование стационарного температурного поля линейных систем с источниками энергии сводится к определению коэффициентов F_ij. Их можно находить экспериментально, теоретическим путем или с помощью аналоговых методов.

Экспериментальный метод заключается в следующем: в некоторой точке j (точка наблюдения системы) помещается температурный зонд (термопара). Определяем зависимость t_j-t_i=f(Ф_j), а потом из уравнения (102) для точки j следует, что эта зависимость будет иметь вид

 

t_j-t_i=F_ijФ_i ,                                                  (103)

 

т.е., зная Ф_i, t_j и t_c, вычисляем F_ij.

Аналитический метод определения тепловых коэффициентов сводится к решению системы уравнений баланса, тепловой энергии или теплопроводности в каждом конкретном случае. Задача по расчету тепловых режимов может быть упрощена за счет специальных конструкций элементов РЭC. Некоторые специальные виды РЭС содержат много одинаковых в конструктивном отношении элементов, повторяющихся в трех измерениях. В этом случае можно использовать прием перехода от реальной неоднородной системы тел к однородному, или, точнее, квазиоднородному, телу. Если нагретая зона состоит из конструктивных одинаковых элементов, распределенных в пространстве в определенной последовательности, то говорят, что система этих нагретых тел обладает дальним порядком, т.е. в любом направлении геометрические и физические свойства периодически повторяются. В этой системе можно выделить элементарный объем, многократным повторением которого можно получить исходную систему. Это называется элементарной ячейкой. Поскольку эффективные коэффициенты теплопроводности и некоторые геометрические размеры такой ячейки и всей системы с дальним порядком совпадают, то можно определить эффективные коэффициенты теплопроводности системы по элементарной ячейке.

Метод определения эффективной теплопроводности можно применить к системе, в которой наблюдается нарушение дальнего порядка (например, не все конструктивные элементы одинаковы в геометрическом отношении, нарушается периодичность их расположения и т.д.). В такой системе можно перераспределить элементы и снова получить систему с дальним порядком. При этом вместо реальных конструктивных элементов следует брать их определенные размеры. Это системы с ближним порядком. Большинство реальных нагретых зон РЭС являются системой с ближним порядком. Использование изложенных приемов позволяет перейти от сложной системы твердых тел с различными физическими и геометрическими параметрами к однородному анизотропному телу.

 

10.2. Принцип местного влияния

 

Этот принцип используется при анализе температурных полей. Он позволяет определить, на каком расстоянии от области, занятой источником тепловой энергии, конфигурация этой области практически не влияет на характер температурного поля в теле  (рис 26).

Изотермические поверхности

ОбластьV

 

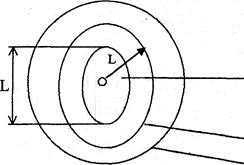
Рис. 26

Этот принцип впервые разработан Дульневым. Было показано, что если источник занимает область V и равномерно распределен по всей области, то за пределами круга радиуса L (наибольший определяющий размер) и с центром в геометрическом центре зоны характер температурного поля такой же, когда весь тепловой поток расположен в центре области.

Пример: рассмотрим температурное поле группы   элементов, расположенных на плате внутри РЭС и являющихся источником тепловой энергии. Они вызовут такое же повышение температуры в отдельных частях аппарата, как равномерно распределенный на плате источник той же мощности. Однако вблизи элементов температурное поле в значительной мере зависит от размеров и конфигурации самих элементов.

Учет двух принципов позволяет сформировать для РЭС сложной конструкции следующие выводы:

1) температурный фон в точке j практически не зависит от форм и размеров удаленных от этой точки деталей, способа монтажа на платах и шасси, а также характера распределения мощностей источников;

2) наведенный перегрев в точке j определяется суммарной мощностью всех источников тепла, действующих в РЭС, за исключением j-го источника. На основании вышеизложенного запишем

t_jф=t_c+F_jф(Ф-Ф_j),

где Ф - суммарная мощность всех источников; t_jф - температурный фон в точке j; t_c - температура среды; Ф_j - мощность источников, действующих в рассматриваемом теле.

 

Вопросы для самоконтроля

 

1. Какой тепловой режим называют стационарным?
2. Как формулируется задача при изучении стационарного режима РЭС?
3. В чём заключается принцип суперпозиции?
4. Перечислите методы определения коэффициентов стационарного температурного поля.
5. Где используется принцип местного влияния и в чём он заключается?
6. Какие выводы можно сформировать с учётом двух принципов?

 

Лекция №11. Тепловые режимы и способы

обеспечения тепловых режимов РЭС

 

11.1. Методы оценки тепловых режимов

 

В настоящее время существует большое количество методов обеспечения тепловых режимов РЭС, которые можно условно разделить на две группы:

1) методы приближенной оценки;

2) экспериментальные аналоговые методы исследования.

Приближенные аналитические методы исследования приводят к системе формул, позволяющих получить информацию о тепловом поле проектируемой системы. Преимущество этого метода перед другими в том, что результат получается в общем виде. Необходимо только указать границы применения полученных формул и хотя бы ориентировочно оценить их точность. Как правило, при разработке методов расчета приходится использовать различные приближенные зависимости, границы которых подразумеваются указанными.

Экспериментальные и аналоговые методы исследования, а также использование ЭВМ позволяют получить информацию о температурном поле конкретной конструкции при заданном режиме ее эксплуатации. Результат имеет частный характер.

Последовательное изучение указанными методами тепловых режимов РЭС в зависимости от изменения тех или иных конструктивных или эксплуатационных параметров дает возможность получить результат опять-таки для группы частных случаев. Возникает весьма сложная задача обобщения полученных результатов, т.е. составление эмпирических формул по данным частным исследованиям.

Эта задача может быть решена различными методами, один из которых - коэффициентный метод, разработанный Дульневым.

Использование различных РЭС показало, что их тепловые режимы обладают высокой стабильностью, т.е. зависят от некоторых общих параметров (габаритных размеров, коэффициента заполнения отдельных блоков и т.д.). Для оценки влияния определяющих параметров на тепловой режим РЭС можно построить весьма грубую модель процесса, которую можно математически описать наиболее простым способом с использованием небольшого числа основных параметров. Эти параметры зависят от других, не учтенных в моделях параметров, причем последние могут изменяться в определенных пределах, диктуемых практическими запросами.

При коэффициентном методе расчета все группы параметров поочередно фиксируются и изучается влияние на тепловой режим только одного параметра. Поясним это на примере.

Пусть главный параметр y зависит от нескольких переменных x₁, x₂,…,x_n:

y = f(x₁, x₂,…,x_i,…,x_n).                                         (104)

 

Тогда, фиксируя все переменные, кроме x_i, находим зависимость y_i = f(x_i). Такую же операцию производим и с остальными аргументами.

Рассмотрим отношение

 

,                                                    (105)

где y₀ – значение функции у при всех фиксированных аргументах ( 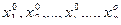), назовем это значение "нулевым" (базовым).

Обычно аргументы 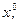 выбираются для какой-либо конкретной типичной конструкции аппарата при определенных наиболее часто встречающихся условиях по эксплуатации.

При выполнении некоторых условий справедливо следующее выражение:

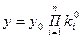,                                 (106)

где 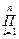 - символ произведения сомножителей 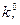; n – число параметров.

Это соотношение выполняется для условий:

а) если у – линейная функция аргументов;

б) если у – нелинейная функция, тогда в окрестностях нулевой точки она должна быть приблизительно линейна и приращение функции должны быть малы по сравнению с ее значениями в нулевой точке.

 

11.1. Способы обеспечения тепловых режимов

 

Многообразие РЭС можно разделить на 2 группы:

1) аппараты с деталями на шасси;

2) аппараты кассетной конструкции.

Аппараты первой группы разделяют на приборы с негерметичными или пылевлагозащитными корпусами и устройства с герметичными корпусами.

 

Способы охлаждения негерметичных аппаратов

 

Конструкции в пылевлагозащищенных корпусах с незначительным тепловыделением допускают отсутствие, каких – либо, специальных устройств для охлаждения. В этих аппаратах перенос выделяемой энергии от теплорассеивающих элементов корпусу и далее в окружающую среду происходит за счет конвекции и теплового излучения, а также при наличии хорошего контакта между шасси корпусом - за счет теплопроводности (рис.27,а).

 

 

 

                      а)                                      б)

 

Рис. 27

На рисунке стрелочками показаны тепловые потоки.

В аппаратах, имеющих перфорации в верхних и нижних частях корпуса, а также шасси происходит интенсивный обмен с окружающей средой за счет вентиляции (рис. 27,б). Выделяемая внутри аппарата тепловая энергия уносится через аппарат снизу вверх воздухом, а также за счет конвекции и излучения наружными поверхностями корпуса.

Конструкции с принудительной вентиляцией применяются, когда тепловыделение элементов в аппаратах достаточно велико. Для создания организованного продува охлаждающего воздуха в противоположных стенках корпуса выполняются вводящие и выводящие устройства (зазоры, щели). Какие-либо отверстия в корпусе, кроме подводящих или отводящих, например, в средней части, приводят к перерасходу воздуха и лишнему расходу энергии на вентилятор (рис. 28).

 

 

 

Рис. 28

 

Для аппаратов с деталями на шасси возможны следующие способы охлаждения:

1. При небольших рассеиваемых мощностях, аппараты в герметичном корпусе не имеют специальных устройств охлаждения. Теплообмен с окружающей средой осуществляется за счет естественной конвекции и теплового излучения (рис. 27,а).

2. Герметичные аппараты со значительным тепловыделением. Усиление теплообмена создается принудительной циркуляцией воздуха внутри корпуса. Принудительная вентиляция повышает теплоотдачу от теплорассеивающих поверхностей к корпусу и далее в окружающую среду, тем самым понижая температуру внутри аппарата (рис. 29).

 

 

 

 

Рис. 29

 

Устройства с микроминиатюрными и миниатюрными компонентами выполняются в виде конструкций ряда плат с установленными модулями и микромодулями, электрически связанными печатным монтажом. Платы объединяются в кассеты, которые весьма удобны в эксплуатации. Кассеты могут размещаться в блоках горизонтально или вертикально в один или несколько рядов. Аппараты на объекте можно установить отдельно друг от друга, и тогда они представляют собой одноблочное устройство, или могут группироваться вместе, образуя многоблочные конструкции (стойки, контейнеры). Способы охлаждения аппаратов кассетной конструкции, наиболее часто встречающиеся в практике радиоконструирования:

1. Аппараты в герметичном корпусе с небольшим тепловыделением плат, не имеющие специальных устройств охлаждения. В таких конструкциях воздушные промежутки между платами весьма малы, поэтому естественная конвекция воздуха внутри конструкции между платами практически отсутствует и телепередача от внутренних поверхностей к корпусу происходит за счет теплопроводности воздуха и плат, а от корпуса тепловой поток рассеивается конвекцией и тепловым излучением (рис. 30).

 

 

 

Рис. 30

2. Естественная вентиляция в аппаратах кассетной конструкции в негерметичном корпусе осуществляется через перфорации между платами. Платы установлены вертикально. При этом рассеиваемый платами тепловой поток уносится протекающим снизу вверх воздухом. Часть тепла отдается в окружающую среду через поверхность корпуса вследствие конвекции и теплового излучения (рис. 31).

 

Рис. 31

 

3. Повышенное тепловыделение плат требует более интенсивного отвода тепла. При этом воздух, поступающий в аппарат, распределяется между платами специальным воздухораспределителем, который из конструктивных соображений размещается на задней поверхности корпуса. Значительная доля рассеиваемого тепла уносится охлаждающим воздухом, а остальная часть передается корпусом в окружающую среду (рис. 32).

 

 

 

Рис. 32

Расчет тепловых режимов РЭС

 

11.2.1. Тепловой режим блока с крупными деталями на шасси

 

На рис. 33 изображен тепловой режим аппарата в герметичном кожухе (а - вид спереди , б - вид сверху).

 

 

 

а)

 

 

б)

 

 

Рис. 33

Используя основные закономерности теории теплообмена, можно записать уравнения:

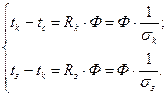                                     (107)

 

Следовательно, при известной температуре среды температура корпуса однозначно определяется мощностью и тепловой проводимостью.

t_k=f(t_c, Ф, s_k);                                (108)

 

t_з=f(t_k, Ф, s_з).                                (109)

 

Для аппарата одного конструктивного исполнения тепловая проводимость зависит от свойств среды, окружающей аппарат, тепло- воспринимаемости поверхности и других параметров. Если рассматривать различные формы аппаратов, то тепловая проводимость будет еще зависеть от геометрических размеров (L,h) и от давления (p) , тогда можно записать:

 

t_k-t_c=V_k=f(p,t_c,t₁,L₂,h,x,Ф).                                    (110)

Известно, что с достаточной для практических расчетов точностью тепловая проводимость s_k любого реального аппарата равна тепловой проводимости куба с равновеликой поверхностью. Следовательно, параметры L₁, L₂, h можно заменить S_k (поверхностью корпуса) и сторона такого куба равна

 

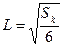.                                              (111)

 

Кроме того, мощность источников тепла можно отнести к поверхности и определить как удельный тепловой поток

 

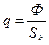.                                          (112)

 

Перепишем (110):

 

V_k=f(q,S_k,t_c,x,p).                                        (113)

 

Используя коэффициентный метод расчета, будем искать зависимость между V_k и определяющими ее параметрами в виде

V_k= V_k0k_x(x=q,S_k,t_c,x,p),                           (114)

 

где         k_x= V_kx/V_k0; k_x – поправочный коэффициент;              (115)

 

 

V_k0= V_k0(q₀,S_k0,x,p₀).                                 (116)

 

Здесь V_k0 – температура перегрева кожуха при базовых значениях всех параметров; V_kx – значение температуры перегрева кожуха при базовых значениях всех параметров, кроме х. Знак 0 характеризует базовые параметры.

Зависимость k_x  от соответствующих х приводятся в литературе в виде графиков для определенного диапазона изменения исходных параметров. Эти диапазоны могут быть определены, например, из стандартов. Так, например, реальный интервал изменения Р будет 5-1520 мм рт.ст., температура среды – до 60 ⁰С и т.д.

Для удобства вычислений

 

V_k0×k_q=V_qk=f(q_k).                                       (117)

 

Учитывая все изложенное выше, запишем для температуры перегрева корпуса РЭС

 

V_k=V_qk×k_sk×k_tc×k_x×k_p.                                    (118)

 

Как следует из зависимости (107), после определения температуры перегрева корпуса можно переходить к расчету перепада температур между нагретой зоной и корпусом Dt_зк. Здесь s будет являться не только функцией геометрических размеров корпуса, но и функцией геометрии воздушных зазоров, функцией геометрии шасси.

 

Dt_зк= Dt_зк (Ф, L₁, L₂, h, t_k, h₁, h₃, l, x_n, p^*),            (119)

 

где h₁, h₃ – размеры воздушных зазоров, между деталями и корпусом, причем для простоты считаем, что h₁=h₃; e_n – приведенная степень черноты; t_k – температура корпуса, равна V_k+t_c, l –определяющий размер шасси, равный 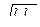(l_1,l₂ размеры реального шасси), т.е. шасси представляется квадратом, равновеликим реальному шасси;     p^*  - давление воздуха внутри корпуса аппарата.

Учтя некоторые особенности, запишем

 

Dt_зк=f(q_з,l,h,t_k,x_n,p*,k_з,h₁/l),                            (120)

 

где k_з – коэффициент заполнения аппарата, т.е. отношение реального объема нагретой зоны к полному объему аппарата; h₁/l – приведенная величина зазора h₁=(h-h₂)/2; x_n – приведенная степень черноты, для 2 тел.

Расчетная формула будет иметь вид

 

Dt_зк=Dt_зк×k_l×k_h×k_кз×k_h1/l×k_p*×k_xn×k_tk.             (121)

 

Погрешность расчета теплового режима аппарата по приведенной методике составляет 25 % по отношению к эксперименту.

 

11.2.2. Алгоритм расчета

 

Дано: L_1, L₂, h; расположение шасси, коэффициент заполнения k_з, степень черноты всей поверхности одинакова x, p, t_c, Ф – рассеиваемая аппаратом мощность.

Необходимо определить температуру корпуса t_k.

Решение:

1. Найдем площадь поверхности:

S_k=2(hL₂+hL₁+L₁×L₂).                           (122)

 

2. Определим удельный тепловой поток:

 

q_k=Ф/S_k.                                     (123)

 

3. Рассчитаем определяющий размер:

 

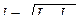.                                    (124)

 

4. Найдем приведенную высоту нагретой зоны:

 

h₂=k_з×h.                                     (125)

 

5. Определим величину зазора и приведенную величину зазора h₁/l:

h₁=0.5(h-h₂).                               (126)

 

6. Вычислим площадь поверхности нагретой зоны. Поскольку шасси плотно заполняет объем корпуса, запишем:

 

S_з=2(h₂L₂+h₂×L₁+L₁×L₂).                       (127)

 

7. Рассчитаем удельный поток нагретой зоны:

 

q_з=Ф/S_k.                                     (128)

 

8. Определим приведенную степень черноты для 2 поверхностей:

 

x_n=x₁×x₂.                                       (129)

 

9. Используя значения q_k,t_c,x,S_k и p, по графикам находим значения коэффициентов V_qk, k_tc,k_x, k_Sk и k_p.

 

10. Определим температуру перегрева корпуса V_k:

 

V_k=V_qk× k_Sk×k_tc×k_x××k_p.                            (130)

 

11. Рассчитаем температуру корпуса аппарата:

t_k = t_c + V_k.                                    (131)

 

 

11.2.3. РЭС в перфорированном корпусе

 

Для снижения температуры в РЭС широко применяется метод перфорирования корпуса и шасси. Процесс теплопередачи в таком аппарате более сложный, чем в предыдущем случае. Выделяемая энергия рассеивается конвекцией и излучением наружными поверхностями корпуса, а также протекающим через аппарат воздухом. Движение воздуха вызвано разностью температур, а следовательно, давлений внутри и снаружи аппарата и в нагретых и холодных частях корпуса. Температура перегрева нагретой зоны зависит от следующих параметров:

 

V_з=f(Ф,h₁,h₂,S₁,S₂,S_ш,S_k1,S_k2,S_зл,S_з1,S_з2,x,t_c).           (132)

 

S₁, S₂ - площадь части поверхности нагретой зоны верхней и нижней крышек корпуса; S_ш - площадь шасси; Sз₁,з₂ - площадь части поверхности нагретой зоны, расположенной в верхнем и нижнем отсеках корпуса; S_зл - площадь поверхности условной нагретой зоны; S_k1, S_k2 - площади отверстий верхней и нижней крышек корпуса

1. Три параметра S₁,S₂,S_ш, можно заменить одним S (приведенная площадь отверстий):

 

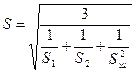.                                      (133)

 

2. При любом смещении шасси его тем не менее можно считать расположенным посередине. Тогда расстояние от шасси до середины верхних и нижних отверстий в кожухе

 

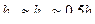,                                             (134)

 

3. Поверхности нагретой зоны верхнего и нижнего отсеков полагают всегда равными:

 

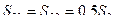,                            (135)

 

S₃ – реальная поверхность нагретой зоны.

 

4. Площади внутренних поверхностей отсеков 1 и 2 тоже равны:

 

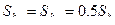,                                        (136)

 

S_k – площадь внутренней поверхности кожуха.

С учетом этих допущений температуру перегрева нагретой зоны можно считать функцией 8 параметров

 

V_з=V_з(Ф,h,S,S_k,S_з,S_зл,x,t_c).                                   (126)

 

Если ввести понятия:

k_з взамен S_зл, S_з/ S_зл вместо S_з, взамен S_k 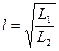, вместо h 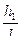, вместо S ,

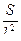то

V_з= V_з(q,l, 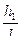, ,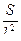k_з, S_з/ S_зл,x, t_c),                                    (138)

а расчетное уравнение

 

V_з=V_q×k_l×k_h×k_з×k_k×k_s×k_x×k_t.                           (139)

 

Погрешность расчета составляет 25 % по отношению к эксперименту. Эта методика в применении к аппаратам с перфорированным корпусом позволяет определить лишь V_з. Температура кожуха аппарата может быть оценена по эмпирической формуле

V_з= 0.3 V_з  .                                          (140)

 

11.2.4. Принудительная вентиляция РЭС

 

Может быть организована по замкнутому и незамкнутому циклам. В первом случае перемещение воздуха происходит по замкнутому каналу из труб, которым к герметическому корпусу РЭС присоединен вентилятор. Внутри корпуса размещены шасси, которые занимают практически все сечение аппарата и делят его объем на 2 отсека, в которых движется воздух. Благодаря такой конструкции и некоторым специальным конструктивным приемам воздух движется параллельно большой стороне шасси. Поскольку корпус герметичный, температура его перегрева V_k может быть определена по формуле (118). Разность температур между нагретой зоной и корпусом является функцией таких параметров:

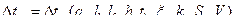.                              (141)

 

Запишем для сравнения формулу (120):

 

Dt_зк=f(q_з,l,h,t_k,x_n,p*,k_з,h₁/l).

 

Из сравнения видно, что в случае принудительной вентиляции в герметичном кожухе перепад температур не зависит от внешнего давления воздуха p , от величины зазора между нагретой зоной и корпусом (h₁/l), но зависит от величины сечения этого зазора. В этом случае необходимы точные данные о сечении канала продувки воздуха (l₁,l₂), площади поверхности реальной нагретой зоны, равна: (S поверхности детали + S шасси) и V – средней скорости вынужденного потока воздуха.

 

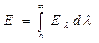,                                                     (142)

 

где F – площадь сечения канала продувки ;

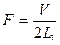 (м²),                                (143)

 

V – объем пустого аппарата (м³); G_v – объемная производительность вентилятора (м³/с); L₁ – длина канала продувки (м).

 

Алгоритм расчета

 

Исходные данные для расчета средней поверхностной температуры t_з нагретой зоны аппарата: L_1, L₂, h, коэффициент заполнения k_з, степень черноты поверхностей x, температура корпуса t_k, поверхность нагретой зоны S, производительность вентилятора G_v, мощности источников тепла Ф.

Необходимо определить температуру нагретой зоны t_з.

Расчет:

1. По (112) находим q.

2. Из (143) определим F.

3. Рассчитаем V (скорость вынужденного потока воздуха).

4. Вычислим x_n (приведенная степень черноты).

5. Найдем значение коэффициента поверхности нагретой зоны:

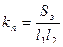.                                                       (144)

6. Определим значение функций по графикам:

k_t=f(t_k); k_v=f(V); k_l1=f(l₁); k_l2=f(l₂);

 

k_e=f(x_n); k_k=f(k_з); k_h=f(h); k_s=f(k_n).

7. Рассчитаем перегрев зоны относительно корпуса по формуле

 

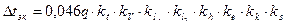.                  (145)

 

8. Найдем температуру нагретой зоны:

 

t_з = t_k + Dt_зк.

 

11.2.6. Принудительная вентиляция многооблочной РЭС

 

Многоблочная РЭС представляет собой конструкцию, в которой несколько блоков расположены один над другим и имеют общий корпус типа шкафа. Такое объединение блоков называется радиоэлектронной стойкой шкафного типа. На шасси монтируются радиодетали. Конструкции вентилируемых стоек, как правило, симметричны относительно вертикальной плоскости, проходящей через середины лицевой и задней стенок корпуса стойки.

Для расчета средних температур нагретой зоны необходимы данные: 1) геометрические размеры корпуса, 2) геометрические параметры нагретой зоны, определяемые конструкцией аппарата, 3) суммарные мощности источников тепла Ф_i, действующие в i-й зоне, 4) температура среды t_c , 5) V_{ск I}  - перегрев воздуха, входящего в i-й отсек, 6) G_p – массовый расход воздуха. Тогда перегрев i-ой нагретой зоны можно определить по формуле

 

V_зi=V_фi×k_вх×k_G×k_t×k_Fi×k_Sзлi×k_Sзi×k_Sзнi  ,             (146)

 

k_Fi – площадь сечения канала прохода воздуха в нагретой зоне; k_Sзлi - площадь измеряемой поверхности нагретой зоны; k_Sзi – площадь теплоотдающей поверхности нагретой зоны (равна сумме теплоотдающих поверхностей радиодеталей шасси); k_Sзнi – площадь наружной части шкафа в пределах i-го (не первого) блока, необходимо учитывать перегрев воздуха в предыдущих блоках.

 

Vвх_i+1 = Vвх +Фi/(10³G_p).                            (147)

 

10³ – теплоемкость воздуха при постоянном давлении.