Моментом силы относительно точки называется вектор, приложенный в этой точке, равный по величине произведению величины силы на кратчайшее расстояние от точки до линии действия силы, называемое плечом, направленный перпендикулярно к плоскости, проходящей через точку и силу, по правилу правого винта, т. е. в ту сторону, откуда совершаемый силой поворот тела, относительно точки виден против хода часовой стрелки. (рис.4)

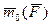
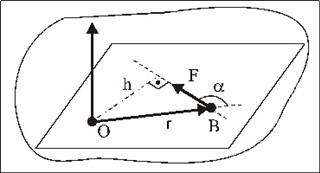
Рис.4.

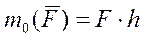(3.1)

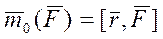Введем в рассмотрение радиус-вектор 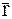, определяющий положение точки B – точки приложения силы .

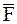                (3.2)

В случае плоской системы сил величину момента силы относительно точки, лежащей в плоскости действия сил, можно рассматривать как алгебраическую величину, равную взятому со знаком плюс или минус произведению модуля силы на плечо:

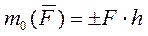                                                                               (3.3)

При этом величина момента берется со знаком плюс, если сила стремится осуществить поворот тела относительно точки против хода часовой стрелки и со знаком минус в противоположном случае.

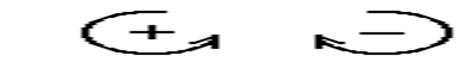
Глава 2. Кинематика

Часть 1. Кинематика материальной точки.

§ 1. Векторный способ задания движения МТ.

Уравнение движения МТ.

Движение МТ при векторном способе задания движения определяется радиус-вектором этой МТ — 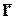, который является функцией времени (уравнение движения):        

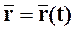.                         (1.1)

Эта функция должна быть однозначной, непрерывной и дважды дифференцируемой. Размерность модуля радиус-вектора в системе СИ: .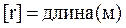

На рис. 1 изображены: точка О - произвольно выбранный, условно неподвижный полюс, точка В - положение МТ в момент времени t, 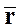- радиус-вектор МТ.

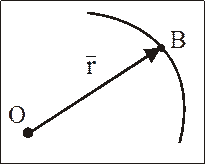
Рис. 1

Траектория МТ

    Определение: Траекторией МТ называется геометрическое место ее последовательных положений в пространстве с течением времени.

    При векторном способе задания движения траекторией МТ является годограф радиус-вектора.

    Годографом любого вектора с неподвижным началом называется кривая, которую описывает конец этого вектора.

Скорость МТ

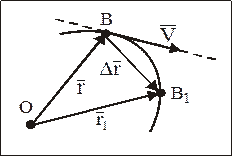
Рис. 2

На рис. 2 изображены: точка В – положение МТ в момент времени t, определяемое радиус-вектором 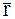, точка В₁ – положение МТ в момент времени t₁, определяемое радиус-вектором .

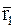Пусть Dt = t₁ – t – приращение времени, а 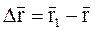 – приращение радиус-вектора, тогда

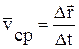называется средней скоростью МТ за промежуток времени Δt, направление которой совпадает с хордой ВВ₁.

Определение : Скоростью МТ в момент времени t называется предельное отношение 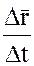 при : .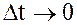

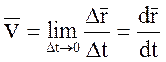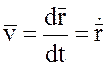.                                   (1.2)

Направление скорости МТ определяется предельным положением приращения радиус-вектора D 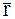 при Dt®0 (В₁®В) и, следовательно, совпадает с направлением касательной к траектории в точке В (рис.2).

    Размерность модуля скорости в системе СИ: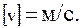

Ускорение МТ

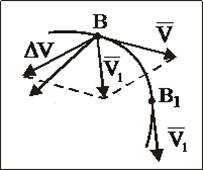
Рис. 3

На рис. 3 изображены: 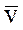- скорость МТ в момент времени t,  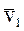– скорость МТ в момент времени t₁.

    Пусть Dt = t₁ – t – приращение времени, а 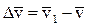 – приращение скорости, тогда  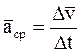называется средним ускорением МТ за промежуток времени Dt.

Определение : Ускорением МТ в момент времени t называется предельное отношение 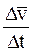 при .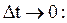

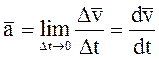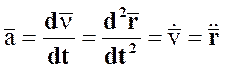.                         (1.3)

Направление ускорения МТ определяется предельным положением приращения скорости 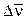 при Dt®0 (В₁®В) и, следовательно,  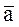направлено в сторону вогнутости траектории (рис. 3).

Размерность модуля ускорения в системе СИ: .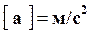

Глава 3. ДИНАМИКА

Часть 1. Динамика МТ