ЛЕКЦИЯ 2
ГОРНАЯ ПОРОДА — СПЛОШНАЯ СРЕДА
Под понятием «сплошная среда» понимается модель такого тела, которое, хотя и состоит из отдельных атомов, молекул, частиц, но занимает пространство непрерывным, сплошным образом, без разрыва сплошности. Горная порода, строго говоря, является дискретной системой. Поэтому лучшей моделью горной породы являлась бы модель, статистически описывающая взаимодействие различных частиц, входящих в её состав, с учетом физического типа взаимодействия между этими частицами. Такая модель горной породы в настоящее время не построена.
Поскольку размеры структурных элементов, входящих в горную породу (минералы, поры), много меньше любого рассматриваемого массива горной породы, то для описания закономерностей изменения напряженно-деформированного состояния используются методы механики сплошной среды: рассматриваются напряжения и деформации в бесконечно малой области и, используя аппарат дифференциального и интегрального исчислений, переходят к рассмотрению напряжений и деформаций в теле большого объема.
Напряженно-деформированное состояние горных пород
Напряженное состояние в «точке». Прежде всего поясним, что под «точкой» мы понимаем физически бесконечно малый объём горной породы. В дальнейшем этот объём мы часто будем представлять в виде куба, параллелепипеда.
При действии на горную породу механических усилий, в ней возникает напряженное состояние, которое характеризуется вектором напряжений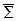 
. Численное значение напряжения определяется отношением F / S , где S —площадка внутри тела, на которую действует сила F. Под площадкой S понимается величина макроскопическая, но физически бесконечно малая.
Напряженное состояние в «точке» считается определенным, т.е. известным, если известна величина модуля вектора напряжений и направление его действия.
Для более детального описания напряженного состояния в «точке»в механике сплошной среды вводится понятие нормального s и касательного t напряжений. Из рис. 1 легко уяснить себе, что они представляют собой в двумерном случае, т.е. на плоскости.
Определяя нормальное напряжение s , следует помнить, что в этом случае направление действия силы F совпадает с направлением единичного нормального вектора ns к площадке S; при определении касательного напряжения t сила F действует в плоскости площадки S, т.е. действует по направлению единичного вектора nt , лежащего в плоскости площадки S (перпендикулярно нормали).
 |
Суммарное действие нормального и касательного напряжений определяет направление действия вектора напряжений и его модуль S:
S = ns.s + nt·t,
S = (s2+ t2)0,5.
Напряженное состояние в «точке» 0 на площадке S определено, если
известен вектор напряжения S или известны составляющие напряжения ,
т.е. напряжения s и t.
В трехмерном пространстве связь между составляющими напряжениями и компонентами вектора напряжений (проекции вектора напряжений Sx, Sy, Sz на оси координат X , Y , Z ) имеет следующий вид:
Sx = nx.sx + ny.txy + nz.txz,
Sy = nx.tyx + ny.sy + nz.tyz,
Sz = nx.tzx + ny.tzy + nz.sz.
 |
Здесь nx, ny, nz есть единичные вектора, направленные по направлению соответствующих осей, sx, sy, sz- нормальные напряжения, txy, tyz, tyz, tzx, tzy —касательные напряжения.
Из рис. 2 можно выяснить направление действия составляющих напряжений и порядок формирования нижних индексов: sx, sy , sz —нормальные напряжения, действующие на площадках Dx, Dy, Dz, перпендикулярных соответствующим координатным осям. Первый индекс в обозначении касательного напряжения указывает на принадлежность к соответствующей площадке, а второй — направление действия напряжения. Например, напряжение tzy действует на площадке Dz и направлено параллельно оси Y.
Суммарное действие составляющих напряжений Sx, Sy, Sz определяет величину модуля вектора напряжений и направление его действия
S = (Sx2 + Sy2 + Sz2)0.5.
S = nx.Sx + ny.Sy + nz.Sz.
Девять составляющих напряжений определяет тензор напряжений Tн, который имеет вид матрицы
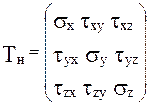
Между касательными напряжениями выполняются следующие равенства
txy = tyx; tzx = txz; tyz = tzy.
Нормальные составляющие напряжения стремятся сократить (при сжатии), либо увеличить (при растяжении) линейные размеры деформируемого тела (стремятся изменить объем «точки», всего тела), касательные же составляющие напряжения стремятся сместить одну часть тела относительно другой (стремятся вызвать изменение формы «точки», тела), произвести сдвиговое разрушение тела.
Одноосное растяжение:
s1 = s2 = 0, s3 < 0 и e1 = e2 = - ne3.
Чистый сдвиг:
s1 = - s3 = t, s2 = 0 и e1 = - e3 = g/2, e2 = 0.
4. Осесимметричное трехосное сжатие (нагружение Кармана):
s1 > s2 = s3 > 0 и e1 > 0, e2 = e3 < 0.
5. Радиальное сжатие (нагружение Бёкера):
s1 = s2 > s3 > 0 и e1 = e2 > 0, e3 < 0.
Инвариан тная вели чина
Вид напряженного состояния
Таблица 4. Значения углов вида и параметров
Инвариан тная вели чина
Вид напряженного состояния
При рассмотрении деформирования образцов горных пород, находящихся в различных напряженных состояниях, необходимо обращать внимание на изменение формы образца gi, которое вызывается интенсивностью касательных напряжений ti и изменения объёма образцов ev = 3eср под действием всестороннего давления sср. Изменения формы и объёма совсем не обязательно должны описываться одинаковыми законами.
Сдвиг является основным видом сопротивления горной породы разрушению при её сложном нагружении, поэтому в дальнейшем мы будем использовать чаще величины ti и gi, чем si и ei.
ЛЕКЦИЯ 2
ГОРНАЯ ПОРОДА — СПЛОШНАЯ СРЕДА
Под понятием «сплошная среда» понимается модель такого тела, которое, хотя и состоит из отдельных атомов, молекул, частиц, но занимает пространство непрерывным, сплошным образом, без разрыва сплошности. Горная порода, строго говоря, является дискретной системой. Поэтому лучшей моделью горной породы являлась бы модель, статистически описывающая взаимодействие различных частиц, входящих в её состав, с учетом физического типа взаимодействия между этими частицами. Такая модель горной породы в настоящее время не построена.
Поскольку размеры структурных элементов, входящих в горную породу (минералы, поры), много меньше любого рассматриваемого массива горной породы, то для описания закономерностей изменения напряженно-деформированного состояния используются методы механики сплошной среды: рассматриваются напряжения и деформации в бесконечно малой области и, используя аппарат дифференциального и интегрального исчислений, переходят к рассмотрению напряжений и деформаций в теле большого объема.
Напряженно-деформированное состояние горных пород
Напряженное состояние в «точке». Прежде всего поясним, что под «точкой» мы понимаем физически бесконечно малый объём горной породы. В дальнейшем этот объём мы часто будем представлять в виде куба, параллелепипеда.
При действии на горную породу механических усилий, в ней возникает напряженное состояние, которое характеризуется вектором напряжений . Численное значение напряжения определяется отношением F / S , где S —площадка внутри тела, на которую действует сила F. Под площадкой S понимается величина макроскопическая, но физически бесконечно малая.
Напряженное состояние в «точке» считается определенным, т.е. известным, если известна величина модуля вектора напряжений и направление его действия.
Для более детального описания напряженного состояния в «точке»в механике сплошной среды вводится понятие нормального s и касательного t напряжений. Из рис. 1 легко уяснить себе, что они представляют собой в двумерном случае, т.е. на плоскости.
Определяя нормальное напряжение s , следует помнить, что в этом случае направление действия силы F совпадает с направлением единичного нормального вектора ns к площадке S; при определении касательного напряжения t сила F действует в плоскости площадки S, т.е. действует по направлению единичного вектора nt , лежащего в плоскости площадки S (перпендикулярно нормали).
| |
Суммарное действие нормального и касательного напряжений определяет направление действия вектора напряжений и его модуль S:
S = ns.s + nt·t,
S = (s2+ t2)0,5.
Напряженное состояние в «точке» 0 на площадке S определено, если
известен вектор напряжения S или известны составляющие напряжения ,
т.е. напряжения s и t.
В трехмерном пространстве связь между составляющими напряжениями и компонентами вектора напряжений (проекции вектора напряжений Sx, Sy, Sz на оси координат X , Y , Z ) имеет следующий вид:
Sx = nx.sx + ny.txy + nz.txz,
Sy = nx.tyx + ny.sy + nz.tyz,
Sz = nx.tzx + ny.tzy + nz.sz.
| |
Здесь nx, ny, nz есть единичные вектора, направленные по направлению соответствующих осей, sx, sy, sz- нормальные напряжения, txy, tyz, tyz, tzx, tzy —касательные напряжения.
Из рис. 2 можно выяснить направление действия составляющих напряжений и порядок формирования нижних индексов: sx, sy , sz —нормальные напряжения, действующие на площадках Dx, Dy, Dz, перпендикулярных соответствующим координатным осям. Первый индекс в обозначении касательного напряжения указывает на принадлежность к соответствующей площадке, а второй — направление действия напряжения. Например, напряжение tzy действует на площадке Dz и направлено параллельно оси Y.
Суммарное действие составляющих напряжений Sx, Sy, Sz определяет величину модуля вектора напряжений и направление его действия
S = (Sx2 + Sy2 + Sz2)0.5.
S = nx.Sx + ny.Sy + nz.Sz.
Девять составляющих напряжений определяет тензор напряжений Tн, который имеет вид матрицы
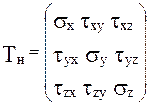
Между касательными напряжениями выполняются следующие равенства
txy = tyx; tzx = txz; tyz = tzy.
Нормальные составляющие напряжения стремятся сократить (при сжатии), либо увеличить (при растяжении) линейные размеры деформируемого тела (стремятся изменить объем «точки», всего тела), касательные же составляющие напряжения стремятся сместить одну часть тела относительно другой (стремятся вызвать изменение формы «точки», тела), произвести сдвиговое разрушение тела.
Напряженное состояние в точке определено, если известны компоненты тензора напряжений.
Тензор напряжений имеет следующие инварианты (invarient - неизменный), т.е. такие алгебраические комбинации компонентов, которые не меняют своих значений при повороте осей тензора (осей координат):
I1(Tн) = sx + sy + sz,
I2(Tн) = sx.sy + sy.sz + sz.sx - txy2 - txz2 - tyz2,
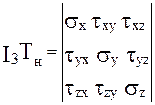
Величина
sср = I1(Tн)/3 = (sx + sy + sz) / 3
определяет среднее нормальное (гидростатическое) напряжение в «точке» и вызывает изменение объёма этой «точки».
Напряженное состояние в «точке» можно представить в виде суммы двух напряженных состояний, описываемых шаровым тензором и тензором-девиатором:
Tн = Tнш + Tнд.
Шаровым тензором называется тензор вида
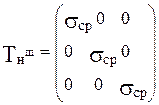
он вызывает изменение только объёма «точки».
Тензор-девиатор Tнд определяет величину отклонения от гидростатического состояния и имеет следующие компоненты:
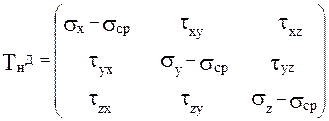
Легко убедиться в том, что первый инвариант тензора-девиатора равен нулю:
(sx -sср) + (sy - sср) + (sz - sср) = 0.
Это означает, что объёмные деформации, вызываемые тензором-девиатором, равны нулю. Касательные напряжения тензора-девиатора вызывают изменения формы «точки».
Произвольное напряженное состояние, в котором находится тело, можно представить в виде суммы двух напряженных состояний: первое представляет собой гидростатическое сжатие тела напряжением sср, а второе напряженное состояние наложено на первое и представляет собой состояние сдвига, обеспечиваемое тензором-девиатором напряжений.
Напряженное состояние в точке определено, если известны компоненты тензора напряжений Tнш и тензора-девиатора напряжений Tнд.
В механике сплошной среды показывается, что любой тензор напряжений может быть приведен к самому простому виду:
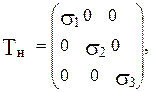
где s1, s2, s3 - главные нормальные напряжения. Они перпендикулярны друг другу и между ними выполняется неравенство s1 > s2 > s3.
Шаровой тензор напряжений и тензор-девиатор напряжений, выраженные через главные нормальные напряжения, имеют вид:
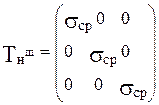
где sср = (s1 + s2 + s3) / 3 и
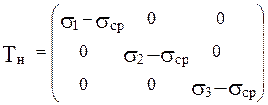
Главные касательные напряжения тензора напряжений Tн выражаются через главные нормальные напряжения
t1 = (s2-s3)/2, t2 = (s1-s3)/2, t3 = (s1-s2)/2,
векторы которых лежат на трех парах взаимно перпендикулярных плоскостей, делящих пополам углы между главными осями тензора напряжений.
Величина главных касательных напряжений тензора напряжений Tн совпадает с величиной главных касательных напряжений тензора-девиатора напряжений Tнд. В справедливости этого легко убедиться, выразив главные касательные напряжения тензора-девиатора через главные нормальные напряжения s 1 - s ср , s 2 - s ср , s 3 - s ср:
t1д = [(s2 - sср) - (s3 - sср)] / 2 = (s2 - s3)/2 = t1,
t2д = [(s1 - sср) - (s3 - sср)] / 2 = (s1 - s3)/2 = t2,
t3д = [(s1 - sср) - (s2 - sср)] / 2 = (s1 - s2)/2 = t3.
В механике сплошной среды большую роль играет первый инвариант тензора напряжений I1(Tн) и второй инвариант девиатора напряжений I2(Tнд). Через главные нормальные напряжения они имеют следующий вид:
I1(Tн) = (s1 + s2 + s3),
I2(Tнд) = [(s1-s2)2 + (s2-s3)2 + (s1-s3)2] / 6.
Через второй инвариант девиатора напряжений вводится понятие интенсивности напряжений:
— интенсивность нормальных напряжений
si = [3.I2(Tнд)]0,5, ( 1 )
—интенсивность касательных напряжений
ti = [I2(Tнд)]0,5. ( 2 )
Через главные нормальные напряжения величины si, ti выражаются следующим образом:
si = [(s1-s2)2 + (s2-s3)2 + (s3-s1)2]0.5 / 20.5 ,
ti = [(s1-s2)2 + (s2-s3)2 + (s3-s1)2]0.5 / 60.5 .
Напряженное состояние в любой точке деформируемого тела определено, если в любой точке этого тела известны значения среднего нормального напряжения sср и интенсивности касательного напряжения ti.
Угол вида напряженного состояния, параметр Лоде. Для характеристики напряженного состояния используются еще две инвариантные характеристики, которые определяются через третий инвариант девиатора напряжений I3(Tнд) = (s1-sср)(s2-sср)(s3-sср):
— угол вида напряженного состояния j(s):
tg j(s) = (s1 —s2)30.5 / (s1 + s2 —2s3),
— параметр Лоде m(s):
m(s) = (2s2 —s1 —s3) / (s1 —s3).
Величины j(s) и m(s) связаны друг с другом соотношением
m(s) = 30.5 ctg (j(s) + p/3).
Величина параметров j(s) и m(s) изменяется в пределах
p/3 ³ j(s) ³ 0, -1≤ m(s) ≤ +1.
Напряженные состояния являются подобными, когда параметры j(s) и m(s) этих состояний равны. Если в процессе нагружения параметр Лоде m(s) остается постоянным, то нагружение считается простым.
Вектор перемещения (вектор деформации) и деформированное состояние в точке. Приложение к твердому телу напряжений и его деформирование приводит к возникновению в теле поля перемещений: каждая точка тела перемещается из одного положения в другое. Такое перемещение точки под действием сил из начального положения в конечное характеризуется вектором перемещения (вектором деформации) U. В векторном виде вектор деформации представим следующим образом:
U = r ' — r,
где r ', r - радиус-векторы, характеризующие положение рассматриваемой
 |
точки после и до приложения сил, соответственно. Вектор U имеет следующие проекции на оси координат X, Y, Z, соответственно: u, v, w.
Полное перемещение деформируемых точек в трехмерном пространстве выражается формулой d = (u2 + v2 + w2)0,5 и является непрерывной функцией координат.
Деформированное состояние в «точке», также как и напряженное состояние, описывается тензором, отвечающим за изменение геометрии рассматриваемой «точки»: изменение её объёма и формы.
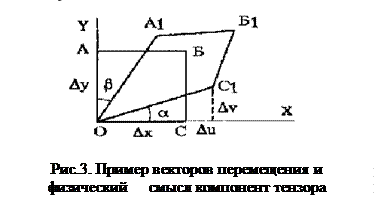
Представим «точку» в виде элементарного куба. Рассмотрим одну грань куба, лежащую в плоскости YX (Рис. 3). До механического нагружения «точки» грань куба ОАБС имеет следующие размеры: ОА = Dy, ОС = Dx. После деформации отрезки ОА, ОС изменят не только свои размеры, но и направления. По этой причине деформация «точки»слагается из линейных (ex, ey, ez) и сдвиговых (угловых) (gxy, gxz, gyx, gyz, gzx, gzy) деформаций. Соответственно этому и тензор деформаций состоит из линейных и сдвиговых компонент:
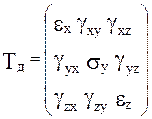
Деформация, соответствующая нормальным напряжениям тензора напряжения, выражается через относительное изменение линейного размера тела l. Линейная деформация может быть абсолютной и в этом случае она опреде-ляется формулой
( lк - lн) = Dl,
где lк —линейный размер тела после деформирования, lн —начальный линейный размер тела, и относительной
e = Dl / lн.
Принято считать относительную линейную деформацию положительной, если она происходит при сжатии, и отрицательной - при растяжении тела.
Линейная относительная деформация, происходящая по направлению действия силы, называется продольной, а перпендикулярно действию силы — поперечной.
Сторона ОС деформируемой «точки» кубика преобразуется в отрезок ОС1, проекция которого на ось X равна величине (Dx + Du), где Du = (du/dx)Dx, Dx >> Du. Отсюда следует, что относительная линейная деформация отрезка ОС, измеряемая в направлении оси X, определится следующим выражением
ex = {Dx —[Dx + (‑Du)]} / Dx = du /dx.
Числитель в написанной формуле обозначает абсолютную деформацию стороны ОС куба. Знак «минус» перед величиной Du обозначает, что рассматривается деформация растяжения тела (при сжатии тела в этой формуле берется знак «плюс».
Линейная относительная деформация элементарного куба в направлении осей Y, Z обозначаются аналогичным образом: ey, ez. Величина этих деформаций выражается через компоненты вектора перемещения v , w:
ey = dv / dy, ez = dw / dz,
Угловые (сдвиговые) деформации в теле возникают при действии касательных напряжений. Сдвиговая деформация физически представляет собой величину изменения прямого угла между гранями элементарного куба при его деформировании. Если рассмотреть, например, одну грань куба, находящуюся в плоскости YX (Рис. 3), то величина угла a, определяющего отклонение направления отрезка ОС1 от его первоначального направления ОС, определится проекциями Du и Dv
tg a = Dv / (Dx + Du) » dv /dx,
т.е. угловая деформация gxy выражается как градиент смещения
gxy = dv /dx.
(Первая буква индекса обозначает ось, от которой происходит движение, вторая буква — к какой оси осуществляется поворот).
Угол b характеризует изменение направления отрезка ОА. Величина угла b определяет угловую деформацию gyx и выражается через проекции отрезка ОА1 на оси X (проекция u) и Y (проекция v):
gyx = tg b = Du / (Dy + Dv) » du /dy.
Суммарное изменение первоначально прямого угла между отрезками ОС и ОА определяется углом y = a + b.
Совместное искажение первоначально прямых углов описывается суммой
tg a + tg b » tg(a+b) = tg y = dv /dx + du/dy
или
gxy = gyx = tg(a+b)/2 = y/2.
Если появление очень малых углов a и b интерпретировать как вращение тела, то угол поворота каждой из рассматриваемых сторон будет равен величине y/2.
Связь между компонентами вектора смещения и компонентами тензора деформации определяется геометрическими уравнениями (уравнения Коши):
ex = du / dx, ey = dv / dy, ez = dw / dz,
gxz = dw / dx + du / dz, gxy = dv / dx + du / dy, gyz = dw / dy + dv / dz.
Физический смысл геометрических уравнений (уравнений Коши) заключается в том, что деформируемое тело является сплошным до, во время и после деформирования. Другими словами, деформирование тела происходит без разрыва вектора перемещения U и, естественно, без разрыва его проекций u, v, w на оси координат.
Тензор деформации Tд , так же как тензор напряжений, имеет три инварианта I1(Tд), I2(Tд), I3(Tд), аналогичные по строению инвариантам тензора напряжений:
I1(Tд) = ex + ey + ez,
I2(Tд) = ex.ey + ey.ez + ez.ex - gxy2 - gxz2 - gyz2,
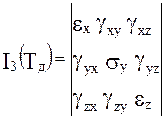
Тензору напряжений, выраженному через главные нормальные напряжения s1, s2, s3, соответствует тензор деформации Tд вида
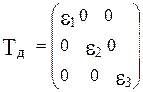
где e1, e2, e3 —есть главные линейные деформации; своим появлением они обязаны действию главных нормальных напряжений.
Разности g1 = e2 —e3 , g2 = e3 —e1, g3 = e1 —e2 определяют величину главных сдвигов.
Как и в случае с тензором напряженного состояния, тензор деформации можно разложить на два тензора, отвечающих за изменение объёма и формы «точки»:
Tд = TдШ + TдД,
где TдШ —шаровой тензор, имеющий вид:
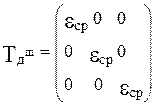
TдД —тензор-девиатор, имеющий вид:
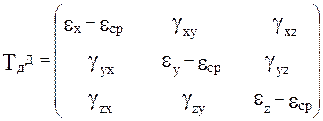
где eср = (ez+ ey+ ex) /3 — средняя линейная относительная деформация. Шаровый тензор определяет изменение объема «точки», а тензор-девиатор отвечает за изменение формы «точки».
Величина
ev = ez + ey + ex
характеризует относительное изменение объёма DV/V элементарного куба, «точки». Этот вывод следует из следующего мысленного опыта. Если к «точке», имеющей форму куба, приложить три взаимно равных сжимающих напряжения, то «точка» будет находиться в состоянии гидростатического сжатия: P = sx = sy = sz, а касательные напряжения в ней будут равны нулю. Приложенные нормальные напряжения вызовут укорочение ребер куба, а значит и уменьшение его объёма. Если первоначальную длину ребра куба принять равной единице, то относительное изменение объёма такого куба ev будет равно следующей величине:
ev = DV / V = [(начальный объём)-(полученный объём)]/(начальный объём) =
[1 - (1‑ex)(1‑ey)(1‑ez)] / 1.
Если не принимать во внимание величины второго и третьего порядка малости (т.е. произведения типа ezey, exezey), то легко получается окончательная формула
ev = ez + ey + ex.
Разделив правую и левую части этого равенства на число 3, получим связь между средней линейной относительной деформацией и относительной объемной деформацией
eср = ev / 3.
Первый инвариант тензора девиатора, т.е. величина
ex - eср + ey - eср + ez - eср
тождественно равна нулю. Физически это означает, что сумма диагональных напряжений тензора девиатора не вызывает изменения объёма деформируемой точки.
Шаровой тензор деформаций Tдш, выраженный через главные линейные деформации, имеет вид:
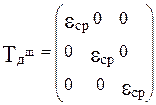
где eср = (e1 + e2 + e3) / 3 , а тензор-девиатор Tдд деформаций задается матрицей следующего содержания:
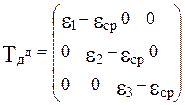
В механике сплошной среды (в теории пластичности) большое значение имеет второй инвариант девиатора деформаций
I2(Tдд) = [(e1 - e2)2 + (e2 - e3)2 + (e3 - e1)2] / 6,
который является суммарной характеристикой изменения формы деформируемого тела. Через второй инвариант девиатора деформаций I2(Tдд) выражаются интенсивность линейных деформаций ei и интенсивность деформаций сдвига gi:
ei = 2×I2(Тдд) / ×3,
gi = 2×I2(Тдд).
Через главные линейные деформации приведенные величины выражаются следующим образом:
ei = ×2.[ (e1 - e2)2 + (e2 - e3)2 + (e3 - e1)2 ]0.5 / 3 , ( 3 )
gi = (2/3)0,5.[ (e1 - e2)2 + (e2 - e3)2 + (e3 - e1)2 ]0.5. ( 4 )
Резюме: Деформация тела заключается в изменении формы, вызванном
Дата: 2019-03-05, просмотров: 215.
