План лекции
1. Общие понятия
2. Фильтры нижних частот
3. Фильтры верхних частот
4. Полосовые фильтры
5. Многозвенные фильтры
6. Проблема согласования фильтров и нагрузки
1. Общие понятия
Электрическими фильтрами называют электронные устройства, избирательно пропускающие спектр входного сигнала.
Необходимость такого рода устройств обоснована тем, что реальные электрические сигналы представляют собой набор спектральных составляющих, которые могут подлежать различной обработке (например, по различным каналам). В виду этого, спектр входного сигнала часто преобразуют, с выделением из него определённых частей (верхней, нижней, или некоторой полосы).
Принцип действия электрического фильтра основывается на частотных зависимостях индуктивного и ёмкостного сопротивлений в цепях переменного тока, известных из курса общей электротехники:
 |
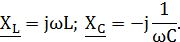
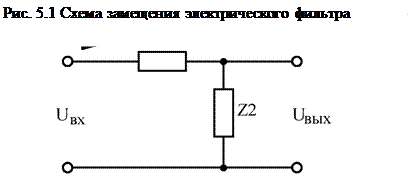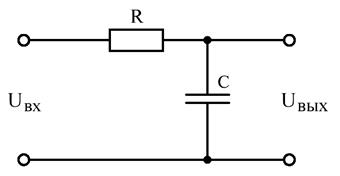
Любой электрический фильтр можно представить в виде четырёхполюсника, изображённого на рис. 5.1.
Тогда выходное напряжение будет равно:
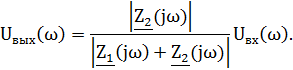
Значит, коэффициент передачи фильтра будет равен:
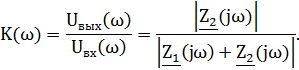
На практике для фильтров принято использовать логарифмический коэффициент передачи, определяемый по формуле:
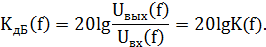
При этом частоту f также откладывают в логарифмическом масштабе, что упрощает работу с такими АЧХ, называемых ЛАЧХ, в практической электронике.
ЛАЧХ электрического фильтра наглядно показывает те области спектра, что передаются без подавления, а также те из них, что будут подавлены и не поступят на его выход.
2. Фильтры нижних частот
Простейший фильтр нижних частот представлен на рис. 5.2. Его коэффициент передачи рассчитывается так:
 |
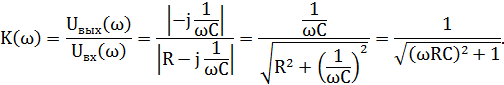
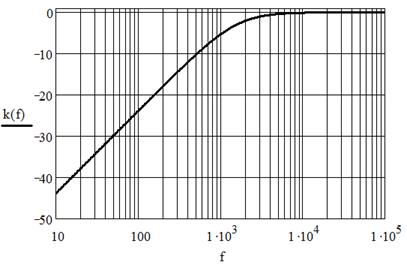
На рис. 5.3 показана ЛАЧХ такого фильтра при R = 100 Ом и С = 1 мкФ.
Видно, что на низких частотах коэффициент передачи равен 0 дБ, то есть, ослабление сигнала отсутствует, но с повышением частоты он резко уменьшается, делая сигнал практически незаметным в остальном спектре.
Частотой среза называют частоту fср, которой соответствует уменьшение уровня сигнала, равное – 3 дБ. По рис. 5.3 видно, что для данного фильтра частота среза имеет порядок 2 кГц.
ФНЧ можно также получить с помощью RL-цепи (см. рис. 5.4). Студентам рекомендуется самим проделать соответствующие преобразования, чтобы доказать это.
 |
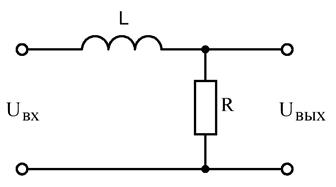
Работу ФНЧ можно объяснить и качественно. Так, для ёмкостного ФНЧ, на очень малых частотах получим большое ёмкостное сопротивление, поскольку XC = 1/(ωC). Тогда его можно уподобить обрыву и всё входное напряжение будет передано на выход. Для высоких частот, напротив, ёмкостное сопротивление будет небольшим, так что выход окажется короткозамкнутым и напряжение на нём будет стремиться к нулю.
Аналогичным образом можно проанализировать и индуктивный ФНЧ, что рекомендуется сделать студенту самостоятельно.
3. Фильтры верхних частот
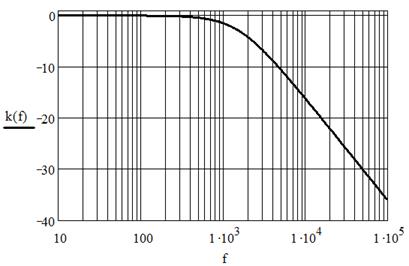
Простейший фильтр верхних частот (ФВЧ) представлен на рис. 5.5. Его коэффициент передачи рассчитывается так:
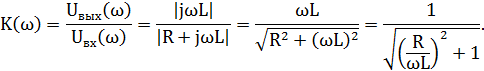
На рис. 5.6 показана ЛАЧХ такого фильтра при R = 100 Ом и L = 10 мГн.
Видно, что на низких частотах коэффициент передачи очень мал, так что сигнал подавлен и не присутствует в спектре, а с повышением частоты его коэффициент ослабления быстро достигает 0 дБ.
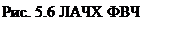
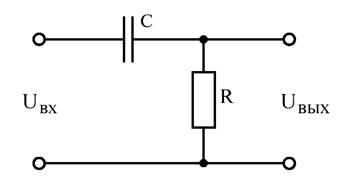
ФВЧ можно также получить с помощью RС-цепи (см. рис. 5.7). Студентам рекомендуется самим проделать соответствующие преобразования, чтобы доказать это.
Работу ФВЧ можно объяснить и качественно. Так, для индуктивного ФВЧ, на очень малых частотах получим малое индуктивное сопротивление, поскольку XL = ωL. Тогда его можно уподобить короткому замыканию и напряжение на выходе будет равно нулю. Для высоких частот, напротив, индуктивное сопротивление будет большим, так выход окажется оборванным и напряжение на нём будет таким же, как и на входе.
Аналогичным образом можно проанализировать и ёмкостный ФВЧ, что рекомендуется сделать студенту самостоятельно.
Итак, ФНЧ передаёт на выход спектральные составляющие входного сигнала, пока частота его меньше определённой частоты, называемой частотой среза (f < fср), и не пропускает спектральные составляющие при противоположном условии (f > fср).
ФВЧ передаёт на выход спектральные составляющие входного сигнала, пока частота его больше определённой частоты, называемой частотой среза (f > fср), и не пропускает спектральные составляющие при противоположном условии (f < fср).
 |
4. Полосовые фильтры
Предназначены для выделения определённой полосы частот, в пределах которой спектр входного сигнала передаётся без подавления (при выполнении условия fср1 < f < fср2). Для всех остальных частот (f < fср1 либо f > fср2) коэффициент передачи фильтра должен быть малым.
Полосовой RC-фильтр показан на рис. 5.8. Он состоит из ФВЧ и ФНЧ, включённых последовательно.
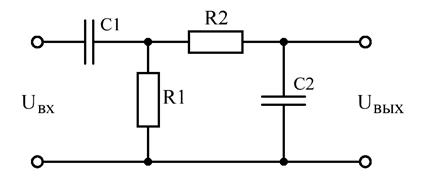
Когда частота сигнала очень мала (f < fср1), то ёмкостное сопротивление XC1 велико и всё напряжение для этих частот приложено к сопротивлению XC1. Когда же частота велика (f > fср2), то сопротивление XC1 пренебрежимо мало, так что C1 можно считать коротким замыканием, но при этом становится малым и сопротивление XC2, что приводит к короткому замыканию выхода и равенства нулю коэффициента передачи фильтра.
На рис. 5.9 показана ЛАЧХ такого фильтра для следующих величин: R1 = 1 кОм, С1 = 1 мкФ, R2 = 50 Ом, С2 = 0,2 мкФ. Видно, что частоты среза такого фильтра имеют порядок 200 Гц и 10 кГц.
 |
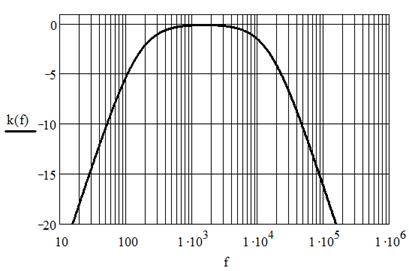5. Многозвенные фильтры
Многозвенные фильтры представляют собой несколько фильтров, включённых последовательно. Можно доказать, что этим можно добиться увеличения скорости спада (или возрастания) затухания для входного сигнала, то есть изменение коэффициента передачи будет происходить резче, что будет благоприятно сказываться на спектре выходного сигнала.
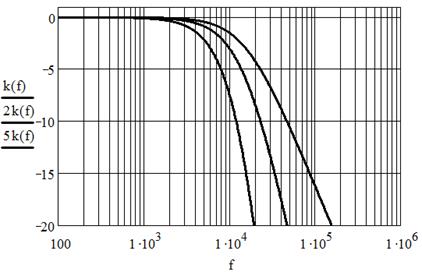
На рис. 5.10 показаны ЛАЧХ для 1, 2-х и 5-ти звенного ФНЧ (см. рис. 5.2) со следующими параметрами: R = 50 Ом, С = 0,2 мкФ.
Из рис. 5.10 видно, что с увеличением количества звеньев, ЛАЧХ становится круче и спектр выходного сигнала может быть преобразован с большей точностью.
При расчёте многозвенных фильтров складывают ЛАЧХ однозвенных фильтров, то есть применяют формулу: kn дБ = nkдБ.
Можно показать, что при применении многозвенных фильтров частота его среза изменяется по отношению к частоте среза однозвенного фильтра. Покажем это на примере емкостного ФНЧ.
Как было показано ранее, АЧХ такого фильтра определяется по формуле:
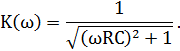
Тогда АЧХ для n-звенного фильтра будет равна:
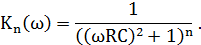
Как и ранее, коэффициент передачи для частоты среза должен быть равен 0,71. Получим следующее уранение для определения частоты среза n-звенного фильтра.
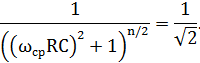
Решая это уравнение получим:
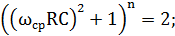
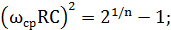
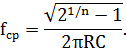
Это означает, что при n→∞, частота среза будет стремить к нулю.
6. Проблема согласования фильтров с нагрузкой
Все рассмотренные выше фильтры имели указанные ЛАЧХ в предположении того, что они работали в режиме холостого хода. Однако на практике электрические фильтры бывают соединены с нагрузкой, по которой протекает ток. Это приводит к тому, что сопротивление нагрузки будет в той или иной степени шунтировать сам фильтр, снижая, таким образом, напряжение на нем.
Рассмотрим для примера емкостный ФНЧ, показанный на рис. 5.2. Определим АЧХ такого фильтра при подключении к нему сопротивления нагрузки Rн. Для простоты будем считать, сопротивление нагрузки имеет активный характер.
Воспользовавшись полученными ранее выражениями, запишем:
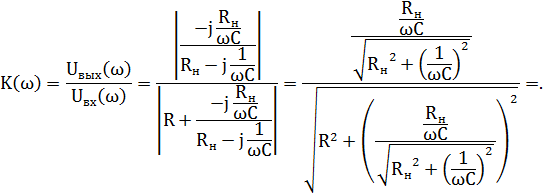
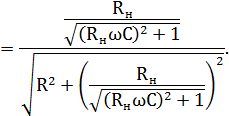
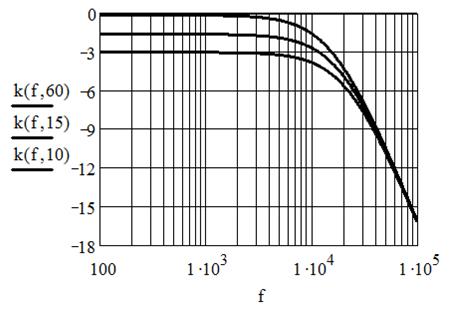Видно, что величина коэффициента передачи теперь будет зависеть не только от частоты, но и от величины сопротивления нагрузки (то есть, фактически, от тока нагрузки). Рассчитанные по этой формуле кривые ЛАЧХ показаны на рис. 5.11 для фильтра с R = 10 Ом, С = 1 мкФ и сопротивлений нагрузки 60, 15 и 10 Ом.
Рис 5.11 ЛАЧХ ФНЧ, рассчитанные для различных значений сопротивлений нагрузки.
Видно, что с увеличением тока нагрузки все большая часть входного напряжения прикладывается к сопротивлению R, уменьшая, таким образом, напряжение на выходе фильтра. Так, например, для Rн = 15 Ом, это уменьшение составляет величину – 1,5 дБ.
Значит, для эффективной работы данного фильтра должно выполняться условие:
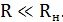
Но тогда возникает проблема согласования этих сопротивлений с емкостным сопротивлением конденсатора. Если частота среза такого фильтра должна определяться только значениями R и C, то нагрузка не должна шунтировать емкостное сопротивление. А это означает, что для них должно выполняться следующее соотношение:
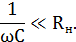
Это условие должно выполняться для возможно меньших значений частот, поскольку с увеличением частоты выполнить его становится проще.
Рассмотрим емкостный ФВЧ, изображенный на рис. 4.7. Его ЛАЧХ будет определяться так:
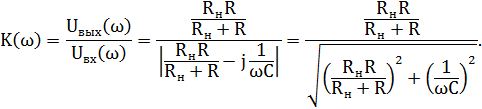
Видно, что этот фильтр будет работать эффективно при противоположном условии
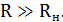
Но в этом случае частота среза такого фильтра будет определяться уже значением сопротивления нагрузки, поскольку ЛАЧХ будет иметь в этом приближении следующую зависимость:
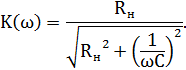
Значит, для эффективной работы такого фильтра необходим стабильный ток нагрузки.
Если же задаться условием
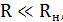
то частоту среза будет определять величина R и величина тока нагрузки не будет иметь на нее влияние, но при этом величина емкости конденсатора может оказаться довольно значительной, поскольку для верхних частот следует соблюсти условие
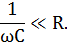
Очевидно, что чем меньше величина R, тем больше должна быть емкость конденсатора ФВЧ, что его емкостное сопротивление соответствовало приведенному выше требованию. Например, для R = 10 Ом и f = 100 Гц, емкость конденсатора должна быть порядка
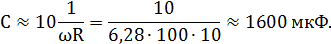
С другой стороны, также должно выполняться условие:
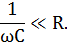
Это условие аналогично рассмотренному ранее, для ФНЧ.
Дата: 2019-03-05, просмотров: 597.
