Таблица 3.3.1
Исходные данные для построения контрольных карт
| № п.п | X1 | X2 | X3 | X4 | X5 | Xср | R |
| 1 | 2,37 | 2,37 | 2,26 | 2,47 | 2,62 | 2,42 | 0,36 |
| 2 | 2,27 | 2,36 | 2,32 | 2,43 | 2,54 | 2,39 | 0,27 |
| 3 | 2,42 | 2,53 | 2,25 | 2,31 | 2,53 | 2,41 | 0,29 |
| 4 | 2,53 | 2,39 | 2,36 | 2,38 | 2,41 | 2,41 | 0,16 |
| 5 | 2,52 | 2,38 | 2,40 | 2,41 | 2,40 | 2,42 | 0,14 |
| 6 | 2,57 | 2,35 | 2,40 | 2,46 | 2,45 | 2,45 | 0,22 |
| 7 | 2,18 | 2,60 | 2,37 | 2,41 | 2,40 | 2,39 | 0,42 |
| 8 | 2,38 | 2,49 | 2,62 | 2,31 | 2,29 | 2,42 | 0,32 |
| 9 | 2,51 | 2,64 | 2,23 | 2,59 | 2,22 | 2,44 | 0,42 |
| 10 | 2,29 | 2,33 | 2,33 | 2,45 | 2,48 | 2,38 | 0,19 |
| 11 | 2,33 | 2,57 | 2,14 | 2,41 | 2,44 | 2,38 | 0,42 |
| 12 | 2,23 | 2,24 | 2,54 | 2,48 | 2,46 | 2,39 | 0,31 |
| 13 | 2,22 | 2,45 | 2,27 | 2,49 | 2,42 | 2,37 | 0,27 |
| 14 | 2,30 | 2,49 | 2,33 | 2,34 | 2,30 | 2,35 | 0,19 |
| 15 | 2,32 | 2,59 | 2,48 | 2,31 | 2,52 | 2,44 | 0,28 |
| 16 | 2,19 | 2,39 | 2,45 | 2,51 | 2,37 | 2,38 | 0,32 |
| 17 | 2,34 | 2,35 | 2,49 | 2,28 | 2,32 | 2,35 | 0,21 |
| 18 | 2,36 | 2,47 | 2,46 | 2,24 | 2,32 | 2,37 | 0,22 |
| 19 | 2,41 | 2,36 | 2,26 | 2,47 | 2,36 | 2,37 | 0,21 |
| 20 | 2,36 | 2,48 | 2,29 | 2,46 | 2,35 | 2,39 | 0,19 |
| 2,40 | 0,27 |
1) Расчет среднего арифметического, размаха, общего среднего арифметического и общего размаха:
Хср=2,40; Rср=0,27.
2) Расчет контрольных границ для карты среднего арифметического:
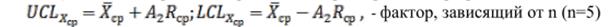
UCLxср=2,40+0,577×0,27 = 2,56
LCLxср=2,40-0,577×0,27 = 2,24
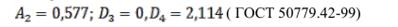
3) Расчет контрольных границ для карты размаха:
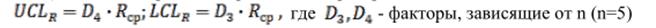
UCLR = 2,144*0,27=0,57
LCLR= 0
4) Контрольные карты имеют следующий вид:
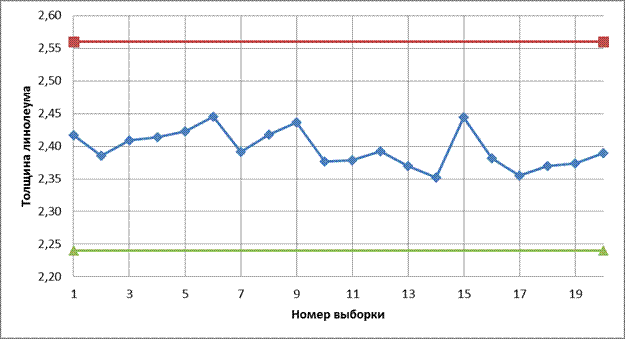
Рис. 3.3.1 Контрольные карты средних
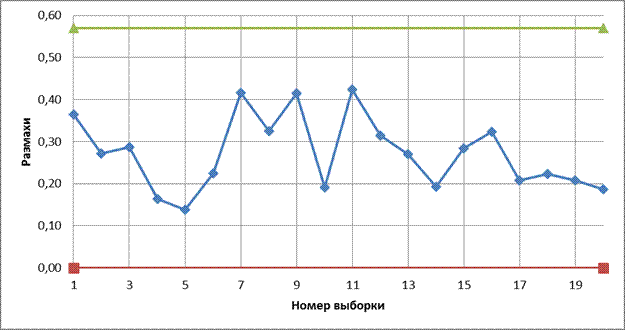
Рис. 3.3.2 Контрольные карты размахов.
Вывод: В построенных картах отсутствует выход результатов за контрольные границы (нет выбросов), периодичность, приближение к центральной линии и линейный тренд, не нарушается случайность распределения точек, т.е. технологический процесс находится в статистически управляемом режиме. Полученные Х и R принять за стандартные значения и использовать при последующем контроле.
Контроль толщины линолеума при помощи np – карты (по альтернативному признаку)
Поскольку задано число дефектов для выборки из 50 изделий и n=const, выбирается биноминальная модель и np контрольная карта. Исходные данные (таблица 3.4.1):
Таблица 3.4.1
| np | np | ||
| 1 | 1 | 16 | 0 |
| 2 | 3 | 17 | 1 |
| 3 | 4 | 18 | 3 |
| 4 | 2 | 19 | 2 |
| 5 | 1 | 20 | 4 |
| 6 | 3 | 21 | 3 |
| 7 | 0 | 22 | 2 |
| 8 | 0 | 23 | 0 |
| 9 | 2 | 24 | 2 |
| 10 | 4 | 25 | 1 |
| 11 | 3 | 26 | 3 |
| 12 | 1 | 27 | 0 |
| 13 | 3 | 28 | 4 |
| 14 | 4 | 29 | 1 |
| 15 | 2 | 30 | 3 |
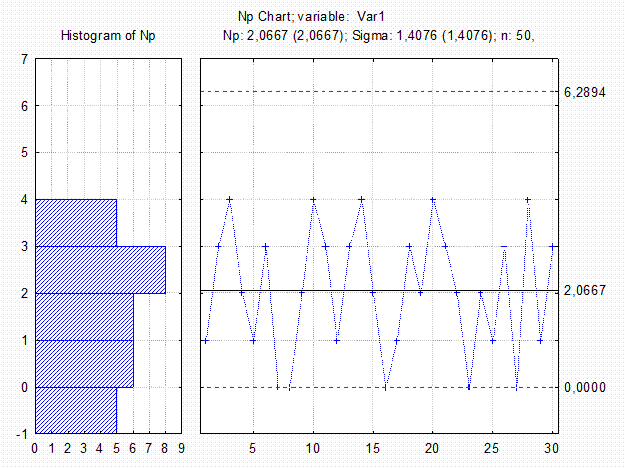 Рис.3.4.1 Контрольная np-карта и гистограмма.
Рис.3.4.1 Контрольная np-карта и гистограмма.
Вывод: Так как выбросы отсутствуют и распределение точек приблизительно симметрично и случайно, то полученное значение 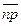 можно принять как стандартное и использовать для дальнейшего контроля.
можно принять как стандартное и использовать для дальнейшего контроля.
Проверка на выбросы
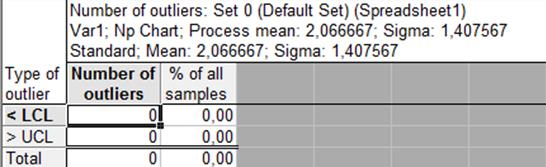
Рис. 3.4.2 Проверка на выбросы np-карты.
Вывод: в нашем случае число значений размаха, находящихся ниже LCL и выше UCL равно нулю.
Гистограмма
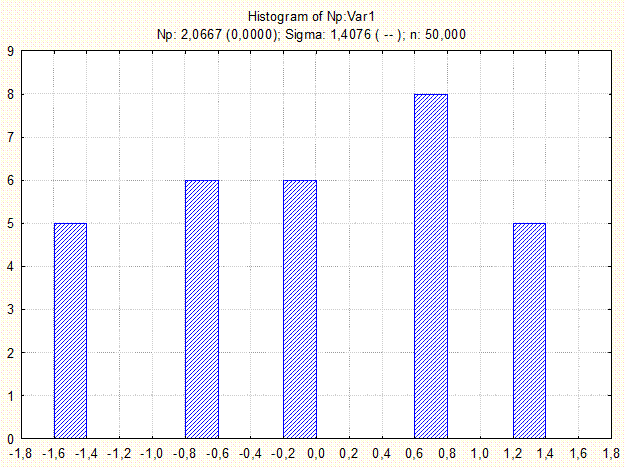
Рис. 3.4.3 Гистограмма для np-карты.
Оперативная характеристика
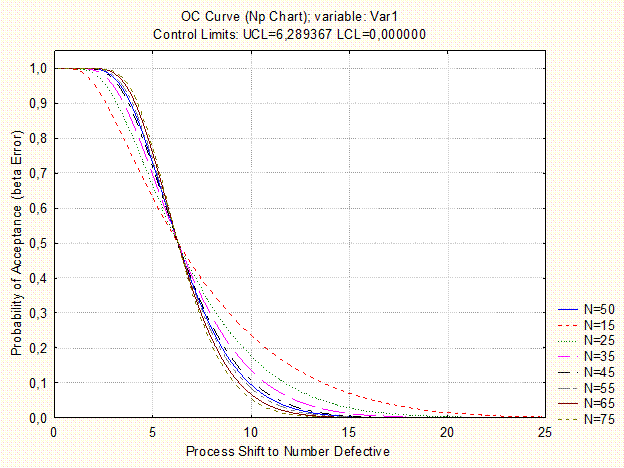 Рис.3.4.4 Оперативная характеристика np-карты.
Рис.3.4.4 Оперативная характеристика np-карты.
Вывод: из графика видно, что чем меньше уровень выборки (N), тем меньше вероятность
Проверка нарушения случайности распределения:
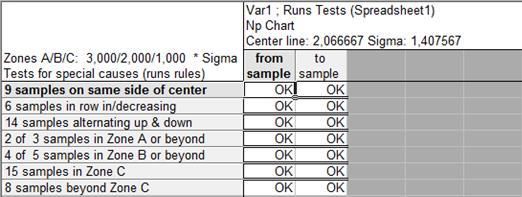
Рис.3.4.5 Проверка нарушений случайности распределения np-карты.
Вывод: нарушений случайности распределения не обнаружено.
Описание контрольной карты (до корректировки)
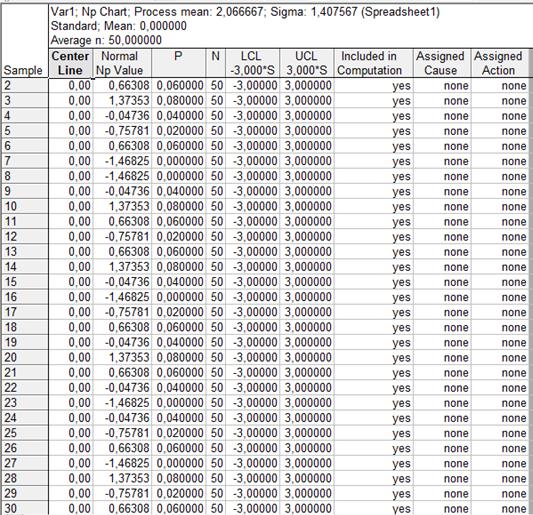
Рис.3.4.6 Описание контрольной np-карты (до корректировки).
Вывод: все полученные значения кроме 30-ого заключены в пределах 6 σ (от LCL=-3; до UCL=3).
1). Расчет параметров контрольной карты: m=30
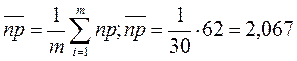
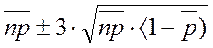
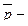 средняя доля дефектов
средняя доля дефектов
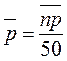 ;
; 
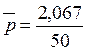 = 0,041
= 0,041
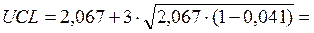 6,289
6,289
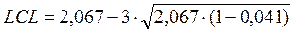 =0
=0
2) Контрольная карта имеет вид:
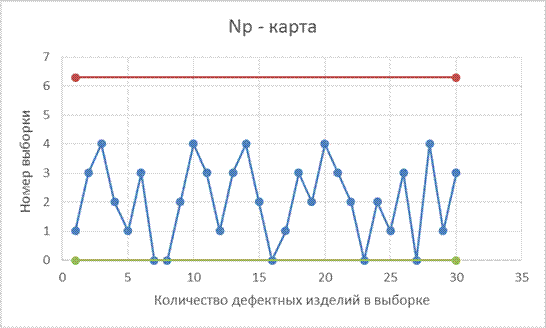
Вывод: Т.к. выбросы отсутствуют и распределение точек приблизительно симметрично и случайно, то полученное значение 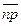 можно принять как стандартное и использовать для дальнейшего контроля.
можно принять как стандартное и использовать для дальнейшего контроля.
Дата: 2019-03-05, просмотров: 344.