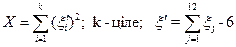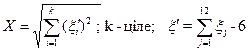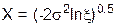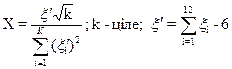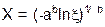Державний вищий навчальний заклад

Української державної академії
Залізничного транспорту
Факультет „ інфраструктура залізничного транспорту ”
Кафедра „АТЗ та ОТ”
С.О.Радковський, А.М.Трунаєв, С.С.Хілобокова
Методичні вказівки
До лабораторних робіт
З дисципліни
«системний аналіз складних систем управління»
Частина 2
Донецьк 2012
Методичні вказівки розглянуті і затверджені на засіданні кафедри «Автоматика, телемеханіка, зв’язок та обчислювальна техніка». Протокол № 9 від 05.06.2012р.
Рекомендовано до друку на засіданні методичної комісії факультету «Інфраструктура залізничного транспорту».
Протокол № 8 від 21.06.2012р.
Укладачі:
С.О.Радковський
А.М.Трунаєв
С.С.Хілобокова
Рецензенти:
к.т.н., доцент В.П.Мороз УкрДАЗТ
к.е.н., доцент А.М.Кремліна ДонІЗТ
ЛАБОРАТОРНА РОБОТА № 4
Тема: Обчислення статистичних показників емпіричного масиву даних та їх графічна інтерпретація.
Мета: Обробка вибірки одновимірних випадкових величин (емпіричного масиву даних), обчислення статистичних показників масиву і їх графічна інтерпретація, визначення теоретичного закону розподілу вибірки випадкових величин.
Обробка одновимірних випадкових величин
Порядок обробки одновимірних випадкових величин наступний:
- побудова варіаційного ряду вибірки одномірної випадкової величини (упорядкування вибірки об'ємом 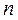 від
від 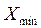 до
до 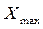 );
);
- визначення орієнтовного значення з округленням в меншу сторону кількості інтервалів групування 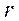 за формулою:
за формулою:
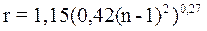 ; (4.1)
; (4.1)
- обчислення ширини інтервалів групування 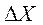 :
:
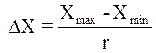 ; (4.2)
; (4.2)
- побудова таблиці 4.1 підрахунку частот, частостей і формування зовнішнього вигляду емпіричного розподілу в інтервалах групування 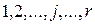 .
.
Таблиця 4.1 - Обробка вибірки одновимірних випадкових величин
| Вибірка випадкових величин
| Номер інтервалу групування | Початок-кінець інтервалу групування (карману)
| Середина інтервалу групування
| Зустрічальність частот
| Частість | |
В інтервалі
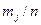
| Накопичена
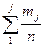
| |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
РАЗОМ: 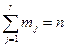
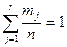 (сума частот що зустрічаються по кожному інтервалу групування повинна дорівнювати одиниці).
(сума частот що зустрічаються по кожному інтервалу групування повинна дорівнювати одиниці).
- керуючись даними таблиці 4.1 виконується побудова графічних характеристик емпіричного розподілу (побудова гістограм).
Гістограма і полігон частот
Нехай 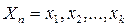 – вибірка обсягу
– вибірка обсягу 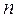 , що містить
, що містить 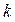 різних варіантів, з генеральної сукупності випадкової величини
різних варіантів, з генеральної сукупності випадкової величини 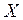 з невідомою щільністю ймовірностей
з невідомою щільністю ймовірностей 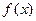 . Наближенням (оцінкою) невідомої щільності ймовірностей можуть служити гістограма або полігон відносних частот. Гістограма і полігон відносних частот призначені для геометричного зображення групованого варіаційного ряду.
. Наближенням (оцінкою) невідомої щільності ймовірностей можуть служити гістограма або полігон відносних частот. Гістограма і полігон відносних частот призначені для геометричного зображення групованого варіаційного ряду.
Гістограма відносних частот представляється у вигляді прямокутників які примикають один до одного з основою
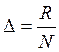 , (4.11)
, (4.11)
рівними ширині інтервалів угруповань, і висотами
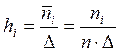 . (4.12)
. (4.12)
Для гістограми відносних частот площа ступінчастої фігури відповідає сумі ймовірностей і дорівнює 1. Площа будь-якого прямокутника гістограми дорівнює ймовірності попадання значень аналізованої випадкової величини в інтервал, відповідний основі прямокутника.
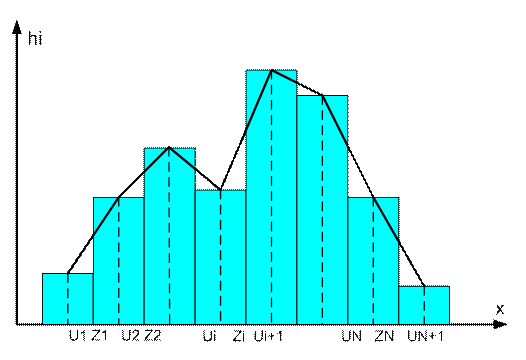
Рисунок 4.1 – Гістограма і полігон відносних частот
Полігоном відносних частот називається ламана, що з'єднує точки 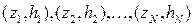 (рис. 4.1), де
(рис. 4.1), де 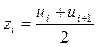 – середини інтервалів і-х угруповань;
– середини інтервалів і-х угруповань; 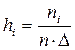 – висоти прямокутників гістограми.
– висоти прямокутників гістограми.
При збільшенні обсягу вибірки та зменшенні довжин інтервалів гістограма і полігон відносних частот наближаються до графіка невідомої функції f(x) – щільності ймовірності генеральної сукупності. По виду гістограми або полігону частот можна висунути гіпотезу про вид розподілу генеральної сукупності (рисунок 4.2).
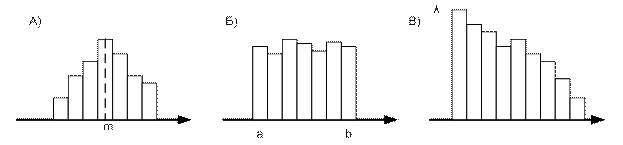
Рисунок 4.2 – Види гістограм
Наприклад, якщо гістограма має вид, представлений на рис. 4.2а, то можна припустити, що генеральна сукупність має нормальний закон розподілу з щільністю ймовірностей
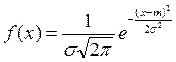 . (4.13)
. (4.13)
Якщо гістограма має вид рис. 4.2,б, що характеризує рівномірний розподіл з щільністю ймовірностей
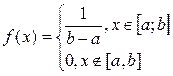 . (4.14)
. (4.14)
Якщо гістограма має вид рис. 4.2,в, що характеризує показовий розподіл з щільністю ймовірностей;
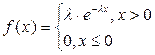 . (4.15)
. (4.15)
Порядок виконання роботи
Налаштувати табличний процесор Excel для роботи з даними. Для цього переконатися в наявності вкладки Аналіз даних у списку падаючого меню кнопки рядка меню Сервіс. В іншому випадку зробити підключення Пакета аналізу. Для цього встановити відповідний прапорець у вікні Надбудови, що відкривається після вибору вкладки Надбудови кнопки рядка меню Сервіс. (Excel 2003).
При використанні Excel 2007 на панелі швидкого доступу необхідно вибрати закладку Дані, за допомогою правої кнопки маніпулятора «миша» вибрати в контекстному меню пункт Настройка панелі швидкого доступу. У даному пункті вибираємо пункт Надбудови в якому вибираємо Пакет аналізу і натискаємо Перейти. В меню Настройки встановлюємо галочку навпроти Пакета аналізу і натискаємо ОК. Після цього в Панелі швидкого доступу з'являється кнопка Аналіз даних.
Вибрати з файлу завдання (видається викладачем) числові дані свого варіанту. З метою отримання варіаційного ряду провести сортування введених випадкових величин за зростанням. Для цього необхідно виділити лівою кнопкою маніпулятора «миша» область сортованих даних. Далі скористатися кнопкою рядка меню Дані, вкладка Сортування (можливий швидкий доступ до даного інструменту при натисканні на кнопку панелі інструментів Стандартна).
Для визначення основних статистичних характеристик необхідно:
1) Вибрати пункт в списку вікна Інструменти аналізу (кнопка Описова статистика рядка меню Сервіс, вкладка Аналіз даних).
2) У вікні Описова статистика в поле з назвою Вхідний інтервал ввести ВХІДНІ ДАНІ. Далі, встановити перемикач Групування в положення – по стовпцях.
3) Вказати ПАРАМЕТРИ ВИВЕДЕННЯ, для чого встановити відповідний пункт Вихідний інтервал. Заповнити поле вихідного інтервалу – область, в якій буде розташовуватися підсумкова таблиця. Для цього вказується номер комірки, в якій буде розташовуватися лівий верхній кут таблиці (поза зоною розрахункової таблиці 4.1).
Далі, встановити прапорець у вікні Підсумкова статистика.
4) Натисненням кнопки ОК вивести таблицю основних статистичних характеристик.
Для заповнення таблиці 4.1 необхідно:
1) Визначити кількість інтервалів групування r і обчислити ширину інтервалів групування X.
2) Використовуючи наявні дані визначити інтервал групування 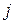 , початок (
, початок ( 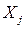 ) і кінець (
) і кінець ( 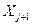 ) інтервалу групування, середину інтервалу групування (
) інтервалу групування, середину інтервалу групування ( 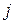 ), зустрічальність частот
), зустрічальність частот 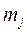 і частість в інтервалі і накопичену частість. Заповнити відповідні стовпчики таблиці 4.1.
і частість в інтервалі і накопичену частість. Заповнити відповідні стовпчики таблиці 4.1.
3) Провести перевірку правильності обчислень, підсумувавши вміст стовпця 5 (Зустрічальність частот). Для цього скористаєтеся кнопкою підсумовування, попередньо виділивши область даних, що підлягає підсумовування. Результат, який виведено в нижній комірці, повинен бути дорівнювати обсягу введеної вибірки.
Аналогічним чином виконується підсумовування вмісту стовпця 6 (частота в інтервалі) результат повинен дорівнювати одиниці. В іншому випадку необхідно визначити і усунути причину невідповідності.
Вибрати пункт Гістограма в списку вікна Інструменти аналізу (кнопка рядка меню Сервіс, вкладка Аналіз даних):
1) У вікні Гістограма в поле з назвою Вхідний інтервал ввести ВХІДНІ ДАНІ.
2) У вікні Гістограма в поле з назвою Інтервал карманів ввести дані стовпця 6 таблиці 1.1.
3) Вказати ПАРАМЕТРИ ВИВЕДЕННЯ, для чого встановити відповідний пункт Вихідний інтервал. Заповнити поле вихідного інтервалу (поза зоною розрахункової таблиці 4.1). Далі, встановити прапорець у вікні Парето, Інтегральний відсоток і Вивід графіка. Натисканням кнопки ОК вивести таблицю частот, частостей емпіричного розподілу, гістограму.
Порівняти отримані дані з даними розрахункової таблиці 4.1.
Для побудови гістограм Густині розподілу ймовірності, Емпіричною функції, Діаграми Парето використовуйте вкладку Діаграма кнопка рядка меню Вставка або кнопку Майстер діаграм панелі інструментів Стандартна.
За зовнішнім виглядом гістограми емпіричної ймовірності, використовуючи графіки теоретичних густин розподілу ймовірностей, що наведені в методичних вказівках, визначити, якому теоретичному закону відповідає зазначена гістограма.
Роздрукувати отримані результати і представити їх в складі звіту про виконання лабораторної роботи. У звіті привести висновки про виконану роботу.
Приклад виконання лабораторної роботи в Excel наведено в додатках.
Зміст звіту
4.5.1 Короткі теоретичні відомості по темі лабораторної роботи.
4.5.2 Розрахунок параметрів в Excel за формулами наведеними в теоретичному матеріалі.
4.5.3 Роздруківку електронної таблиці Excel виконану для свого варіанту (приклад наведено у Додатку В).
4.5.4 Графіки залежності відповідно до завдання.
4. 6 Контрольні питання
4.6.1 Наведіть порядок обробки одновимірних випадкових величин.
4.6.2 Яке призначення мають гістограма і полігон відносних частот?
4.6.3 Які основні статистичні характеристики вибірки Ви знаєте, приведіть визначення і формули.
Література
4.7.1 Вентцель Е.С. Теория вероятностей [Текст]. Е.С. Вентцель М: Наука., 1969.- 576 с.
4.7.2 Шторм Р. Теория вероятностей. Математическая статистика [Текст]. Статистический контроль качества. Р.Шторм − М.: Изд-во «Мир», 1970.- 368 с.
4.7.3 Гмурман В.Е. Теория вероятностей и математическая статистика [Текст]: Учебное пособие для вузов. В.Е. Гмурман– 8-е издание, М.: Высшая школа, 2003. – 479 с.
4.7.4 Гмурман В.Е. Руководство к решению задач по теории вероятностей и статистике [Текст]: Учебное пособие для вузов. В.Е. Гмурман – М.: Высшая школа, 2002. – 405 с.
ЛАБОРАТОРНА РОБОТА № 5
Тема: Параметричне оцінювання та критерії згоди
Мета: оцінка параметрів і перевірка гіпотези про відповідність емпіричних даних передбачуваному теоретичному розподілу.
Теоретичні відомості.
5.1.1 Загальна постановка задачі.
У математичній статистиці часто виділяють особливий розділ, в якому розглядається перевірка гіпотез. Статистична перевірка гіпотез застосовується для того, щоб використовувати отриману за вибіркою інформацію для судження про закон розподілу генеральної сукупності. Зазвичай статистична гіпотеза перевіряється за допомогою критеріїв згоди, які дозволяють оцінити відповідність того чи іншого теоретичного закону розподілу деякого емпіричного ряду розподілу.
Критерії згоди повинні дати відповідь на питання, чи можна прийняти для даного емпіричного розподілу модель, відображену деяким теоретичним законам розподілу. У математичній статистиці близькість емпіричних і теоретичних розподілів оцінюють за допомогою критеріїв згоди, які розроблені багатьма вченими. Одні з них оцінюють вірогідність розбіжності між емпіричними і теоретичними даними (критерії згоди Пірсона та Колмогорова), інші конкретно відповідають на питання про можливість збігу даного емпіричного розподілу і вибраного теоретичного закону (критерії згоди Романовського і Ястремського).
5.1.2. Методи параметричної оцінки законів розподілу.
Для визначення чисельних значень параметрів передбачуваних розподілів застосовуються методи: лінійного оцінювання, імовірнісних сіток, квантилів, максимального правдоподібності і моментів.
Найбільш простим і поширеним є метод моментів, який полягає в тому, що початкові і центральні моменти теоретичного розподілу, що залежать від невідомих параметрів цього розподілу, прирівнюються до статистичних моментів. При цьому статистичні початкові і центральні моменти відповідно 1-го і 2-го порядків визначаються за формулами
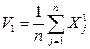 ;
; 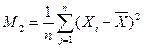 . (5.1)
. (5.1)
Формули взаємозв'язку аналітичних моментів з невідомими параметрами теоретичних розподілів наведені в таблиці Б1. Додатку Б. У результаті вирішується система рівнянь, що зв'язує параметри з моментами, звідки визначаються оцінки відповідних параметрів.
5.1.3. Критерій хі-квадрат Пірсона.
Відомий англійський статистик К. Пірсон в 1900 році запропонував для оцінки розбіжності між емпіричними і теоретичними частотами критерій, який заснований на визначенні величини хі-квадрат (χ2).
Критерій – Пірсона є найбільш простим і поширеним і заснований на виразах
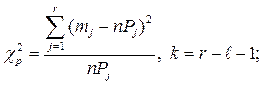 (5.2)
(5.2)
де 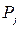 – теоретичні значення ймовірності розподілу в інтервалі групування r;
– теоретичні значення ймовірності розподілу в інтервалі групування r;
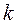 – число ступенів свободи при кількості обчислених параметрів розподілу –
– число ступенів свободи при кількості обчислених параметрів розподілу – 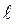 .
.
По заданому значенню рівня значимості (0,2 ... 0,005) і підрахованому 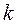 з таблиць критерію Пірсона (файл лаб_5.xls) визначається значення
з таблиць критерію Пірсона (файл лаб_5.xls) визначається значення 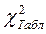 .
.
Для прийняття гіпотези про згоду емпіричних даних з теоретичним необхідно, щоб
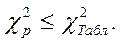 (5.3)
(5.3)
1.4. Критерій Романовського.
Романовський В.І. запропонував використовувати критерій хі-квадрат в іншому вигляді. Значення критерію обчислюється за формулою:
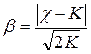 , (5.4)
, (5.4)
де 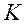 - число ступенів свободи.
- число ступенів свободи.
У тому випадку, якщо 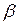 за абсолютним значенням менше 3, то розбіжність між емпіричним і теоретичним розподілами вважається несуттєвою і прийнятий закон розподілу можна прийняти в якості моделі емпіричного розподілу. Якщо ж вираз
за абсолютним значенням менше 3, то розбіжність між емпіричним і теоретичним розподілами вважається несуттєвою і прийнятий закон розподілу можна прийняти в якості моделі емпіричного розподілу. Якщо ж вираз 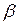 більше 3, то розбіжність між розподілами істотна.
більше 3, то розбіжність між розподілами істотна.
Ставлення Романовського ґрунтується на тому, що математичне сподівання χ дорівнює числу, а дисперсія – подвоєному числу ступенів свободи (2 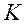 ). В цьому випадку імовірність відхилення величини хі-квадрат на
). В цьому випадку імовірність відхилення величини хі-квадрат на 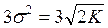 близька до одиниці.
близька до одиниці.
Зміст звіту
5.3.1 Короткі теоретичні відомості по темі лабораторної роботи.
5.3.2 Розрахунок параметрів в Excel за формулами, що наведені в теоретичному матеріалі та в прикладі.
5.3.3 Роздруківку електронної таблиці Excel, що виконана для варіанту за завданням (приклад наведено у додатку Г).
5.3.4 Графік залежності відповідно до прикладу.
5.4 Контрольні питання
5.4.1 Для чого проводиться статистична перевірка гіпотез про закон розподілу генеральної сукупності?
5.4.2 Які Ви знаєте критерії згоди і для чого вони застосовуються?
5.4.3 Яке призначення критерію хі-квадрат Пірсона і для чого застосовується?
5.4.4 Яке призначення критерію Романовського і для чого застосовується?
5.4.5 Які теоретичні закони розподілу Ви знаєте? Охарактеризуйте графіки їх теоретичних густин розподілу ймовірностей.
Література
5.5.1 Вентцель Е.С.. Теория вероятностей. М: Наука., 1969.- 576 с.
5.5.2 Шторм Р. Теория вероятностей. Математическая статистика. Статистический контроль качества. − М.: Изд-во «Мир», 1970.- 368 с.
5.5.3 Быкадоров Р.В. Критерии согласия при статистических исследованиях процесса ткачества. .ИГТА, 2002 – 28 с.
5.5.4 Гмурман В.Е. Теория вероятностей и математическая статистика: Учебное пособие для вузов. – 8-е издание, М.: Высшая школа, 2003. – 479 с.
ЛАБОРАТОРНА РОБОТА №6
Тема: Моделювання дискретних і безперервних випадкових величин.
Мета - генерування величин із заданим законом розподілу, яка відображає випадкові фактори, що впливають на поведінку складних систем
Теоретичні відомості
В процесі аналізу і проектування імітаційних моделей стохастичних систем виникає необхідність завдання різних випадкових впливів або імітування стохастичних процесів. Подібні ситуації зумовлюють необхідність програмної генерації випадкових чисел з деяким законом розподілу. Нехай потрібно отримати (змоделювати) реалізацію випадкової величини X з щільністю розподілу 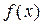 . Дане завдання вирішується шляхом моделювання випадкової величини
. Дане завдання вирішується шляхом моделювання випадкової величини 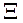 , рівномірно розподіленої на інтервалі [0; 1), і перетворення послідовності випадкових чисел
, рівномірно розподіленої на інтервалі [0; 1), і перетворення послідовності випадкових чисел 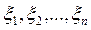 в послідовність
в послідовність 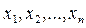 . У загальному випадку перетворення можна реалізувати за допомогою деякої функції
. У загальному випадку перетворення можна реалізувати за допомогою деякої функції
X=ψ(Ξ), (6.1)
що зв'язує випадкові числа з рівномірним розподілом з випадковими числами з заданим законом розподілу. Перетворення (6.1) може бути виконано різними методами.
6.1.1 Метод зворотних функцій.
Нехай потрібно отримати значення випадкової величини 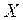 , розподіленої в інтервалі
, розподіленої в інтервалі 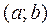 з щільністю ймовірності
з щільністю ймовірності 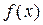 .
.
Стандартний метод моделювання заснований на тому, що інтегральна функція розподілу 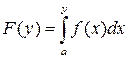 будь якої безперервної випадкової величини рівномірно розподілена в інтервалі
будь якої безперервної випадкової величини рівномірно розподілена в інтервалі 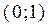 , тобто для будь випадкової величини
, тобто для будь випадкової величини 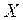 з щільністю розподілу
з щільністю розподілу 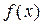 випадкова величина рівномірно розподілена на інтервалі
випадкова величина рівномірно розподілена на інтервалі 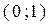 .
.
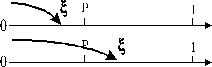
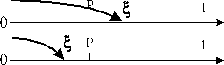
Тоді випадкову величину 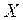 з довільною густиною розподілу
з довільною густиною розподілу 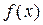 (див. рис. 6.1) можна розрахувати за наступним алгоритмом:
(див. рис. 6.1) можна розрахувати за наступним алгоритмом:
1. Необхідно згенерувати випадкову величину 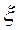 (значення випадкової величини
(значення випадкової величини 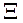 ), рівномірно розподілену в інтервалі
), рівномірно розподілену в інтервалі 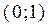 .
.
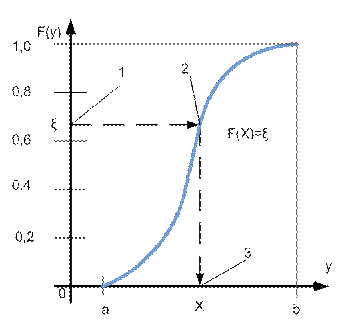
Рисунок 6.1 - Графічне зображення методу зворотних функцій
2. Прирівняти генероване випадкове число відомої функції розподілу 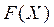 і отримати рівняння
і отримати рівняння
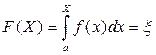 .
.
3. Вирішуючи рівняння 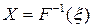 , знаходимо шукане значення
, знаходимо шукане значення 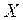 .
.
Такий спосіб отримання випадкових величин називається методом зворотних функцій.
6.1.2 Моделювання неперервних величин.
Стандартний метод моделювання (метод зворотних функцій) заснований на співвідношенні функції розподілу 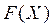 неперервної випадкової величини
неперервної випадкової величини 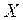 , щільності розподілу ймовірності
, щільності розподілу ймовірності 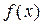 і рівномірно розподілених
і рівномірно розподілених 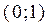 випадкових чисел r формулою
випадкових чисел r формулою
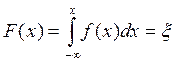 .
.
Тому, отримання випадкової величини 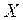 полягає в обчисленні виразу
полягає в обчисленні виразу 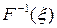 - функції, зворотної по відношенню до
- функції, зворотної по відношенню до 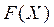 шляхом інтегрування, де це можливо, щільності
шляхом інтегрування, де це можливо, щільності 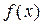 , рис. 6.1.
, рис. 6.1.
Для показового розподілу з щільністю
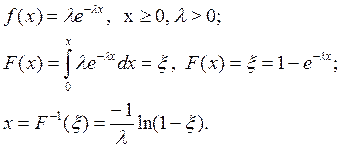
Зворотні функції безперервних випадкових величин основних розподілів наведені в таблиці 6.1.
6.1.3 Методи моделювання дискретних величин.
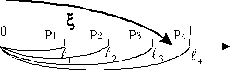
Для моделювання дискретної випадкової величини Х, при довільному законі розподілу (таблиця 6.1) її можливі значення 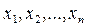 розташовують у порядку зменшення відповідних ймовірностей, тобто
розташовують у порядку зменшення відповідних ймовірностей, тобто 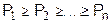 , причому, як повна група подій. В результаті порівняння випадкового числа з довжинами сусідніх відрізків, наприклад
, причому, як повна група подій. В результаті порівняння випадкового числа з довжинами сусідніх відрізків, наприклад 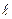 2<ξ≤
2<ξ≤ 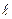 , формулюється висновок про те, яке значення прийняла дискретна випадкова величина, в нашому випадку
, формулюється висновок про те, яке значення прийняла дискретна випадкова величина, в нашому випадку 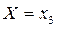 . Якщо
. Якщо 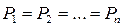 - випадок дискретного рівномірного розподілу, то
- випадок дискретного рівномірного розподілу, то 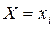 , де i = 1 + ЦЧ (
, де i = 1 + ЦЧ ( 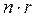 ), Цч - ціла частина добутку
), Цч - ціла частина добутку 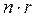 .
.
Моделювання розподілу Пуассона (закон рідких подій) з параметром 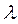 ґрунтується на твердженні, що величини
ґрунтується на твердженні, що величини 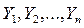 незалежні і мають експоненційний розподіл з математичним очікуванням, рівним 1. При цьому ціле невід'ємне число
незалежні і мають експоненційний розподіл з математичним очікуванням, рівним 1. При цьому ціле невід'ємне число 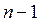 підпорядковується розподілу Пуассона, якщо
підпорядковується розподілу Пуассона, якщо
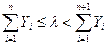 , де
, де 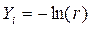 чи
чи 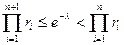 .
.
Біномінальний розподіл з параметрами - числом 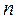 -незалежних випробувань і незмінною ймовірністю
-незалежних випробувань і незмінною ймовірністю 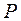 моделюється наступним чином: формується
моделюється наступним чином: формується 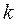 -послідовностей з
-послідовностей з 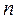 -незалежних випробувань випадкових чисел
-незалежних випробувань випадкових чисел 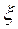 , які порівнюють із заданою вірогідністю
, які порівнюють із заданою вірогідністю 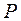 . Число ж випадків виконання умови
. Число ж випадків виконання умови 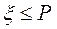 в кожному випробуванні і приймають за послідовність випадкових величин
в кожному випробуванні і приймають за послідовність випадкових величин 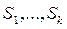 розподілених по біномінальному закону.
розподілених по біномінальному закону.
Таблиця 6.1-Алгорітми моделювання величин
| № | Найменування розподілу, (параметри) |
Алгоритми моделювання величини X | ||
| 1 | 2 | 3 | ||
| 1 | Ряд розподілу дискретної величини X (Pi) |
| ||
| 2 | Пуассона, (а) |
| ||
| 3 | Біноминальне (Бернуллі), (n,P) | 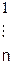
| 
| 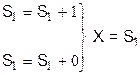
|
| 
| 
| ||
| 4 | Рівномірне, (a,b) |
| ||
| 5 | Показове, ( 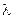 ) [експоненційне] ) [експоненційне]
|
| ||
| 6 | Нормальне, (m, 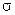 ) [Гаусса] ) [Гаусса]
|
| ||
| 7 | Логарифмічно нормальне, (g, 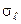 ) )
|
| ||
| 8 | Гамма, ( 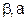 ) )
|
| ||
| 1 | 2 | 3 | ||
| 9 | 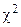 , (k) [хі-квадрат] , (k) [хі-квадрат]
|
| ||
| 10 | 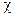 , (k) [хи] , (k) [хи]
|
| ||
| 11 | Релея, ( 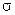 ) )
|
| ||
| 12 | Стьюдента, (k) |
| ||
| 13 | Вейбулла, (a,b) |
| ||
6.2. Порядок виконання роботи:
6.2.1 Налаштувати табличний процесор Excel для роботи з даними. Для цього переконатися в наявності вкладки Аналіз даних у списку спадаючого меню кнопки рядка меню Сервіс. В іншому випадку зробити підключення Пакета аналізу. Для цього встановити відповідний прапорець у вікні Списку надбудов, що відкривається після вибору вкладки Надбудови кнопки рядка меню Сервіс.
6.2.2 Відповідно до виданого завданням (файл лаб_6.xls) помістити в осередки значення параметрів безперервних і дискретних розподілів. У вихідних даних вибрати діапазон відповідно для рівномірного розподілу (0, 1) і для нормального розподілу (-3, 3) розподілення випадкових чисел. Для цього встановити курсор у відповідній комірці і в рядку меню Сервіс вибрати вкладку Аналіз даних, інструмент аналізу - Генерація випадкових чисел.
6.2.3 У вікні Генерація випадкових чисел в поле з назвою Число змінних ввести - 1; в поле з назвою Кількість випадкових чисел - 40; в поле з назвою Розподіл - Рівномірний (Нормальне). В підвікно з назвою Параметри для Рівномірного - між 0 і 1 (для Нормального - середнє 0, стандартне відхилення 1); в поле з назвою Випадкове розсіювання - (будь-яке число в інтервалі 1 ... 32767); в підвікно з назвою Параметри виводу визначити початкову адресу виведення даних. Після закінчення вибору параметрів полів - натиснути клавішу ОК.
6.2.4 Аналогічно пункту 2.3 виконати моделювання для розподілів - Рівномірного, Нормального, Пуассона, біноміального. Для розподілів - експоненційного, Лог-нормального, Релея і Вейбулла, використовуючи алгоритми моделювання (таблиця 6.1) виконати програмування осередків. Далі, використовуючи метод протягування заповнити стовпці.
6.2.5 При моделюванні дискретного розподілу слід враховувати, що воно характеризується значенням і відповідним йому значенням вірогідності (задати самостійно). Діапазон повинен складатися з двох стовпців: лівого, що містить число і правого, що містить ймовірність появи цього числа. Сума ймовірностей повинна дорівнювати 1. Результати моделювання дискретного розподілу помістити у відповідний стовпець. Для цього у вікні Генерація випадкових чисел в поле з назвою Число змінних ввести - 1; в поле з назвою Число випадкових чисел - 40; в поле з назвою Розподіл - Дискретне. В під вікно (обкладинку) з назвою Параметри для дискретного розподілу виберіть вхідний інтервал значень ймовірностей, який відповідає стовпцях 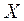 і
і 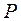 (провести спільну вибірку даних стовпців).
(провести спільну вибірку даних стовпців).
6.2.6 Запрограмувати обчислення середнього арифметичного і стандартного відхилення за стовпцями.
6.2.7 Для кожного змодельованого масиву побудувати гістограми розподілу частот.
6.2.8 Оформити звіт по лабораторній роботі. У складі звіту до лабораторної роботи повинні бути присутніми: таблиця результатів моделювання заданих розподілів (роздруківка випадкових величин для 5 табличних рядків), розрахункові значення середніх арифметичного і квадратичного відхилення, гістограми розподілу частот, висновки про виконану роботу.
Зміст звіту
6.3.1 Короткі теоретичні відомості по темі лабораторної роботи.
6.3.2 Роздруківка електронної таблиці Excel, виконана для свого варіанту (приклад показано у додатку Д).
6.3.3 Гістограми змодельованих розподілів із зазначенням виду.
6.4. Варіанти завдання для моделювання
Вихідні дані для моделювання випадкових величин знаходяться у файлі завдання до лабораторної роботи і видаються викладачем під час занять.
6.5. контрольні питання
6.5.1 Які способи моделювання випадкових величин ви знаєте?
6.5.2 У чому полягає сутність методу зворотних функцій?
5.3 Наведіть і охарактеризуйте метод моделювання безперервних величин.
6.5.4 Наведіть і охарактеризуйте метод моделювання дискретних величин.
6.5.5 Які закони розподілу неперервних випадкових величин ви знаєте?
5.6 Які закони розподілу дискретних випадкових величин ви знаєте?
6.5.7 Які алгоритми моделювання дискретних і безперервних величин ви знаєте, приведіть та охарактеризуйте кожен з них
Література
6.6.1 Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1977. – 366 с.
6.6.2 Гмурман В.Е. Руководство к решению задач по теории вероятности и математической статистике. – М.: Высшая школа, 1979. – 334 с.
Методичні вказівки
До лабораторних робіт
З дисципліни
«системний аналіз складних систем управління»
Частина 2
Донецьк 2012
Трунаєв Андрій Михайлович,
Методичні вказівки
До лабораторних робіт
З дисципліни
«системний аналіз складних систем управління»
Частина 2
Технічні редактори Григор’єва Л.В.,
Чупахіна Н.А.
| Підписано до друку 18.09.2012. Формат 60×84/16. Папір писальний. Гарн. Times New Roman. Друк на ксероксі Умов.друк.арк. 1,5. Наклад 30 прим. Зам. № . |
| Донецький інститут залізничного транспорту Надруковано в редакційно-видавничому відділі ДонІЗТ Свідоцтво про внесення до Держ. реєстру від 22.06.2004р., серія ДК №1851 83018, м. Донецьк – 18, вул.Горна,6. |
Зміст
| Лабораторна робота № 4 ………………………………… | ||
| 4.1. | Обробка одновимірних випадкових величин …............... | |
| 4.2. | Визначення основних статистичних характеристик вибірки ……………………………………………………. | |
| 4.3. | Гістограма і полігон частот ……………………………… | |
| 4.4. | Порядок виконання роботи ……………………………… | |
| 4.5. | Зміст звіту ………………………………………………… | |
| 4.6. | Контрольні питання ……………………………………… | |
| 4.7. | Література ………………………………………………… | |
| Лабораторна робота № 5 ………………………………… | ||
| 5.1. | Теоретичні відомості …………………………………….. | |
| 5.2. | Порядок виконання роботи ...……………………………. | |
| 5.3. | Зміст звіту ………………………………………………… | |
| 5.4. | Контрольні питання ……………………………………… | |
| 5.5. | Література ………………………………………………… | |
| Лабораторна робота №6 …………………………………. | ||
| 6.1. | Теоретичні відомості …………………………………….. | |
| 6.2. | Порядок виконання роботи ……………………………... | |
| 6.3. | Зміст звіту ………………………………………………… | |
| 6.4. | Варіанти завдання для моделювання …………………… | |
| 6.5. | Контрольні питання ……………………………………… | |
| 6.6. | Література ………………………………………………… | |
| Додатки …………………………………………………… |
державний вищий навчальний заклад

Дата: 2019-03-05, просмотров: 937.
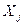
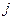
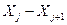
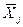
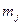
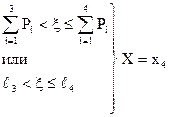
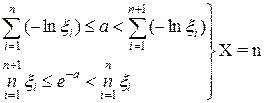
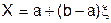
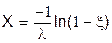
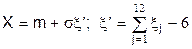
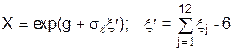
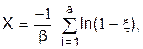 a – ціле
a – ціле