РАСШИРЕНИЕ КЛЮЧА ( Key Expansion )
K = (10, 2, 6, 8)
| 1010 | 0110 |
| 0010 | 1000 |
| W1 | 1010 | 0010 |
| W2 | 0110 | 1000 |
;
;
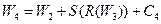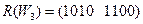
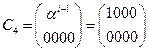W2 =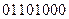 
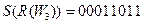
C4 =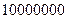 
____________
W4 =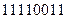 
| W3 | 1100 | 1010 |
| W4 | 1111 | 0011 |
;
;
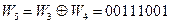
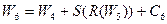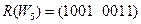
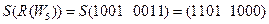
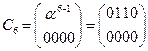W4 =11110011
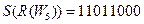
C6 = 01100000
____________
W6 = 01001011
| W5 | 0011 | 1001 |
| W6 | 0100 | 1011 |
; 
; 
;
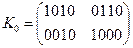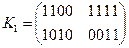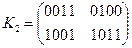ШИФРОВАНИЕ
· 
· 
· 
· 
· 
· 
· 
· 
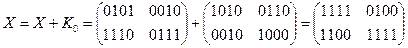
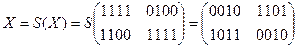
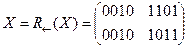
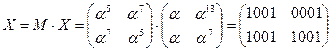
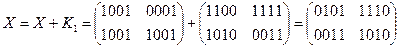
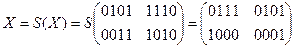
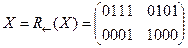
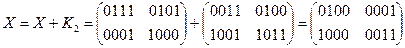
Зашифрованный текст: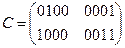 
ДЕШИФРОВАНИЕ
· 
· 
· 
· 
· 
· 
· 
· 
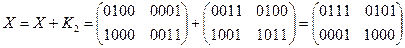
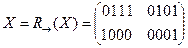
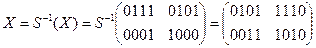
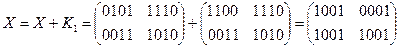
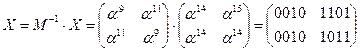
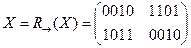
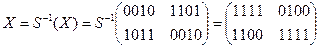
Расшифрованный текст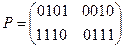 
соответствует исходному.
Пример выполнения Задания2. .
Алгоритм шифрования RSA. Цифровая подпись
Группа 2091, вариант №7.
|
| открытый ключ | шифро- текст | |
| № | n=p*q | e | c |
| 7 | |||
667
17
219
Расшифровать текст C = 219.
Открытый ключ n = p*q = 667.
e = 17
Подбираем простые числа p и q. Получаем следующее представление n:
n = p*q = 667 = 23 * 29.
Найдем значение функции Эйлера:
j(n) = (p-1)(q-1) = 22*28 = 616.
В соответствии с алгоритмом шифрования RSA число е выбирается так, чтобы значения j(n) и e были взаимно простыми. Числа 638 и 17 являются взаимно простыми: у них нет общего делителя кроме единицы. Таким образом, число e выбрано корректно.
(638, 17) = 1
Чтобы расшифровать сообщение, необходимо найти секретный ключ d. Для этого нужно решить сравнение I степени:
ed º 1 mod j(n)
17d º 1 mod 616
Для решения сравнения воспользуемся алгоритмом Евклида:
17 = 616*0 +17
616 = 17*36 + 4
17 = 4*4 + 1
4 = 1*4 + 0
| n | -2 | -1 | 0 | 1 | 2 | 3 |
| qn | 0 | 36 | 4 | 4 | ||
| Pn | 0 | 1 | - | - | - | - |
| Qn | 1 | 0 | 1 | 36 | 145 | - |
d = (-1)k-1Qk-1 mod j(n) = 145 mod 616 = 145
Дешифрование
Открытый текст M = Cd mod n
M = 219145 mod 667 = 52
Открытый текст M = 52.
Шифрование
C = Me mod 667 = 5217 mod 667 = 219
Подпись
Открытый ключ e = 17
Открытый ключ n = 667
Секретный ключ d = 145
Возвести открытый текст (его хэш) в степень d по модулю n, получаем подпись.
sign = 52 ^ 145 mod 667 = 634
Проверка подписи
Получатель получает сообщение с подписью, подпись возводит в степень e по модулю n.
634 ^ 17 mod 667 = 52
При проверке получено сообщение (хэш сообщения), следовательно верификация сообщения пройдена успешно.
Пример выполнения Задания2
Алгоритм шифрования RSA. Цифровая подпись
Выработка собственных секретных ключей.
, 
, 
, 
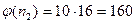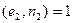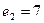
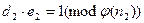
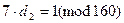
| -2 | -1 | 0 | 1 | 2 | 3 |
| - | - | 0 | 22 | 1 | 6 |
| 1 | 0 | 1 | 22 | 23 | 160 |
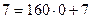
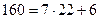
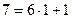
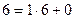
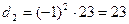
Дешифровка посланного сообщения.
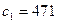
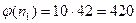
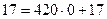
| -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| - | - | 0 | 24 | 1 | 2 | 2 | 2 |
| 1 | 0 | 1 | 24 | 25 | 74 | 173 | 420 |
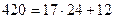
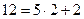
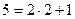
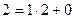
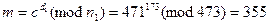
3. Выработка общего ключа (алгоритм Диффи-Хеллмана).
GF(19)
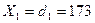
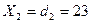
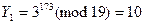
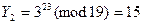
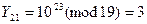
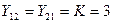
Верификация расшифрованного сообщения.
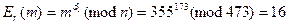
Итоговое (расшифрованное, верифицированное) сообщение: (355, 16).
Пример выполнения Задания3.
Алгоритм Диффи-Хеллмана
Открытый элемент Р задан в таблице 3 – графа 2. Найти примитивный элемент поля. Считая, что секретный ключ каждого участника равен номеру студента в списке группы i , вычислить ключ обмена для участника с номером 35 – i по алгоритму Диффи-Хэллмана.
Вариант № 7, группа 2091 (№ 1)
Номер в списке группы i = 7
Номер группы k = 1
P = 43
Открытый элемент P = 43. Найти примитивный элемент поля. Секретный ключ каждого участника i = 7, вычислить ключ обмена для участника с номером 35.
GF(43) = <0, 1, 2, 3, …, 40, 41, 42>
Найдем примитивный элемент поля GF(43).
Требуется найти такое число, принадлежащее интервалу [2,42], которое при возведении в 42-ю степень по модулю 43 будет давать в результате единицу. Если же единица будет получена раньше, чем при возведении в 42-ю степень, результаты возведения в степень начнут повторяться, и через выбранный элемент не удастся представить все элементы поля. Исходя из таких соображений, получаем несложный алгоритм нахождения примитивных элементов поля GF(43).
Алгоритм нахождения примитивных элементов поля GF(43).
int _tmain(int argc, _TCHAR* argv[])
{
long int mem, i, j, num, deg, modul, res;
unsigned char mas[44];
deg = 0; modul = 43; mem = 2;
while (mem < 42)
{
num = mem; deg = 0;
while (deg != 42)
{
res = 1; deg = 0;
for (i = 0; i < 42; i++) mas[i] = 0;
do
{
res = res*num; res = res % modul;
deg++; mas[deg] = res;
}
while(res != 1);
num++;
}
std::cout << num-1 << std::endl;
for (i = 0; i < 42; i++)
{
for (j = 0; j < 42; j++)
{
if ((i != j) && (mas[j] == mas[i]))
std::cout << "Wrong" << std::endl;
}
mem = num;
}
}
return 0;
}
В результате выполнения программы получим следующие значения:
3, 5, 12, 18, 19, 20, 26, 28, 29, 30, 33, 34
Выберем значение α = 20. Найдем элементы поля.
| α = 20 α2 = 13 α3 = 2 α4 = 40 α5 = 26 α6 = 4 α7 = 37 α8 = 9 α9 = 8 α10 = 31 α11 = 18 | α12 = 16 α13 = 19 α14 = 36 α15 = 32 α16 = 38 α17 = 29 α18 = 21 α19 = 33 α20 = 15 α21 = 42 α22 = 23 | α23 = 30 α24 = 41 α25 = 3 α26 = 17 α27 = 39 α28 = 6 α29 = 34 α30 = 35 α31 = 12 α32 = 25 α33 = 27 | α34 = 24 α35 = 7 α36 = 11 α37 = 5 α38 = 14 α39 = 22 α40 = 10 α41 = 28 α42 = 1 |
Секретный ключ участника А: XA = 7.
Секретный ключ участника B: YB = 35-7 = 28.
Открытый ключ участника А: 
Открытый ключ участника B: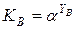 
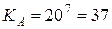
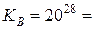15 * 208 = 6
Обменный ключ участника А: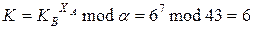 
Обменный ключ участника B: 
Значения обменного ключа для А и В совпадают.
Обменный ключ: K = 6
Пример выполнения Задания3. Алгоритм Диффи-Хеллмана
Открытый элемент Р задан в таблице 3 – графа 2. Найти примитивный элемент поля. Считая, что секретный ключ каждого участника равен номеру студента в списке группы i , вычислить ключ обмена для участника с номером 35 – i по алгоритму Диффи-Хэллмана.
Вариант № 15, группа 2091 (№ 1)
Номер в списке группы i = 15
Номер группы k = 1
P = 37
Открытый элемент P = 37. Найти примитивный элемент поля. Секретный ключ каждого участника i = 15, вычислить ключ обмена для участника с номером 35-15 = 20.
GF(37) = <0, 1, 2, 3, …, 35, 36, 37>
Найдем примитивный элемент поля GF(37).
Требуется найти такое число, принадлежащее интервалу [2,37], которое при возведении в 37-ю степень по модулю 37 будет давать в результате единицу. Если же единица будет получена раньше, чем при возведении в 36-ю степень, результаты возведения в степень начнут повторяться, и через выбранный элемент не удастся представить все элементы поля. Исходя из таких соображений, получаем несложный алгоритм нахождения примитивных элементов поля GF(37).
Алгоритм нахождения примитивных элементов поля GF(37).
int _tmain(int argc, _TCHAR* argv[])
{
long int mem, i, j, num, deg, modul, res;
unsigned char mas[38];
deg = 0; modul = 37; mem = 2;
while (mem < 36)
{
num = mem; deg = 0;
while (deg != 36)
{
res = 1; deg = 0;
for (i = 0; i < 36; i++) mas[i] = 0;
do
{
res = res*num; res = res % modul;
deg++; mas[deg] = res;
}
while(res != 1);
num++;
}
std::cout << num-1 << std::endl;
for (i = 0; i < 36; i++)
{
for (j = 0; j < 36; j++)
{
if ((i != j) && (mas[j] == mas[i]))
std::cout << "Wrong" << std::endl;
}
mem = num;
}
}
}
В результате выполнения программы получим следующие значения:
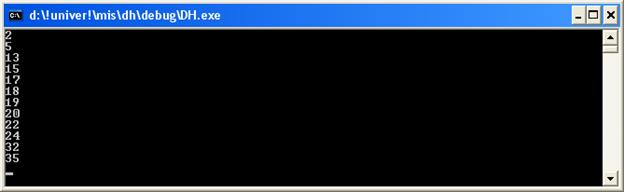
2, 5, 13, 15, 17, 18, 19, 20, 22, 24, 32, 35
Выберем значение α = 2.
Секретный ключ участника А: XA = 15.
Секретный ключ участника B: YB = 35-15 = 20.
Открытый ключ участника А: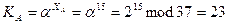 
Открытый ключ участника B: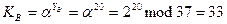 
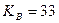
Обменный ключ участника А: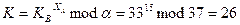 
Обменный ключ участника B: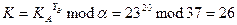 
Значения обменного ключа для А и В совпадают.
Обменный ключ: K = 26
Пример выполнения Задания4. Традиционное шифрование
Вариант № 7, группа 2091 (№ 1)
Номер в списке группы i = 7
Номер группы k = 1
| № | P | Открытый текст | способ |
| 7 | 43 | Повадки волчьи, а душа заячья | Хилла, цифирь Петра 1 |
Задание
Зашифровать поговорку, выбранную из списка в соответствии с номером студента в группе:
1. С помощью способов, указанных в таблице
2. С помощью ключа, где в качестве ключа используем
a. константу c = 3
b. следующую в списке поговорку, используя алфавит
Z33 = (А….Я, е=ё + пробел).
c. псевдослучайную последовательность, сгенерированную линейным рекуррентным генератором. Зашифровать 7 первых символов, используя алфавит Z32 и равномерный код. ПСП (псевдослучайная последовательность) генерируется матрицей 5*5.
Полученное сообщение подписать, используя алгоритм Эль-Гамаля. В качестве хэш-функции использовать сумму пятиразрядных блоков по модулю 2.
1.1 Цифирь Петра Первого (аналог)
| а | б | в | г | д | е | ё | ж | з | и | й |
| я | ты | они | она | от | кому | ему | им | сейчас | потом | иногда |
| к | л | м | н | о | п | р | с | т | у | ф |
| когда | всегда | часто | редко | метко | редко | криво | прямо | мы | нам | налево |
| х | ц | ч | ш | щ | ъ | ы | ь | э | ю | я |
| направо | вперед | назад | вбок | вниз | вверх | бегом | шагом | быстро | четко | туда |
Повадки волчьи, а душа заячья
Жирным шрифтом выделены фрагменты, которые не несут смысловой нагрузки в шифре. Остальной текст может быть расшифрован согласно таблице выше.
редко но метко они или я и от меня но когда лето потом зима
они метко всегда назад стреляли шагом потом уходили
я пришел
от нам повезло вбок я получил
сейчас я туда назад шагом снова туда пойду
Способ Хилла
Будем использовать следующий алфавит.
| а | б | в | г | д | е | ж | з | и | й | к |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| л | м | н | о | п | р | с | т | у | ф | х |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| ц | ч | ш | щ | ъ | ы | ь | э | ю | я | _ |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
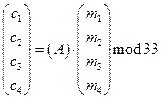Пусть 
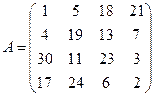
Например:
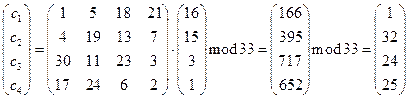
Разобьем поговорку на блоки по четыре буквы:
| ПОВА | ДКИ_ | ВОЛЧ | ЬИ_А | _ДУШ | А_ЗА | ЯЧЬЯ |
| (16 15 3 1) | (5 11 9 33) | (3 15 12 24) | (27 9 33 1) | (33 5 20 25) | (1 33 8 1) | (32 24 27 32) |
| (1 32 24 25) | (24 16 16 7) | (6 27 9 3) | (27 22 21 17) | (19 2 29 26) | (1 16 18 1) | (23 4 27 26) |
| АЯЧШ | ЧППЖ | ЕЬИВ | ЬХФР | ТБЪЩ | АПТА | ЦГЬЩ |
Итак, после преобразования по методу Хилла, получаем:
ПОВАДКИ_ВОЛЧЬИ_А_ДУША_ЗАЯЧЬЯ = АЯЧШЧППЖЕЬИВЬХФРТБЪЩАПТАЦГЬЩ
Шифрование с помощью пароля
c = 3
Алфавит
абвгдеёжзийклмнопрстуфхцчшщъыьэюя_
Исходный текст:
Повадки_волчьи,_а_душа_заячья
После шифрования получим:
Тсегжнлвесоьэл,вгвжцыгвкгбьэб
С помощью текста
В качестве пароля взять следующую в списке поговорку.
Пароль:
По хозяину и собаке честь
Алфавит
Z33 = (А….Я, е=ё + пробел).
абвгдежзи й к л м н о п р с т у ф х ц ч ш щ ъ ы ь э ю я _
012345678 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
Пароль
По_хозяину_и_собаке_честьПо_хозяину и собаке честь
Исходный текст:
Повадки_волчьи_а_душа_заячья
Зашифрованный текст:
Юьбхтсжзпакяыщнб_ошччдштъейю
Расчеты:
п + п = (15 + 15) mod 33 = 30 = ю
о + о = (14 + 14) mod 33 = 28 = ь
_ + в = (32 + 2) mod 33 = 1 = б
х + а = (21 + 0) mod 33 = 21 = х
о + д = (14 + 4) mod 33 = 18 = т
з + к = (7 + 10) mod 33 = 17 = с
я + и = (31 + 8) mod 33 = 6 = ж
и + _ = (8 + 32) mod 33 = 7 = з
н + в = (13 + 2) mod 33 = 15 = п
у + о = (19 + 14) mod 33 = 0 = а
_ + л = (32 + 11) mod 33 = 10 = к
и + ч = (8 + 23) mod 33 = 31 = я
_ + ь = (32 + 28) mod 33 = 27 = ы
с + и = (17 + 8) mod 33 = 25 = щ
о + _ = (14 + 32) mod 33 = 13 = н
а + б = (0 + 1) mod 33 = 1 = б
а + _ = (0 + 32) mod 33 = 32 = _
к + д = (10 + 4) mod 33 = 14 = о
е + у = (5 + 19) mod 33 = 24 = ш
_ + ш = (32 + 24) mod 33 = 23 = ч
ч + а = (23 + 0) mod 33 = 23 = ч
е + _ = (5 + 32) mod 33 = 4 = д
с + з = (17+ 7) mod 33 = 24 = ш
т + а = т
ь + я = (28+ 31) mod 33 = 26 = ъ
п + ч = (15+ 23) mod 33 = 5 = е
о + ь = (14 + 28) mod 33 = 9 = й
_ + я = ю
После шифрования получаем:
Юьбхтсжзпакяыщнб_ошччдштъейю
Дата: 2019-03-05, просмотров: 253.
