Задания на лабораторные работы
Задание 1
Зашифровать и расшифровать открытый текст с помощью упрощенного алгоритма VS-AES. Выполнить 2 итерации. Параметрами алгоритма являются:
· Многочлены для ByteSub :
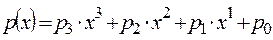 и
и 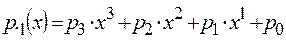
· с коэффициентами из GF(2), которые можно задать двоичным вектором.
Например, многочлен 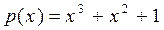 можно задать двоичным вектором (1 1 0 1) или десятичным числом “13 ”, соответствующим этому вектору.
можно задать двоичным вектором (1 1 0 1) или десятичным числом “13 ”, соответствующим этому вектору.
· Многочлен первой степени для MixColumn c коэффициентами из 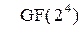
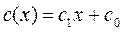 , задаваемый двумя числами из
, задаваемый двумя числами из 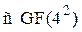 .
.
Например, пара чисел (3.8) соответствует многочлену
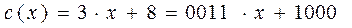
· Ключ К, состоящий из четырех полубайтов, выраженных десятичными числами.
Например, К = 12 1 4 14 = 1100 0001 0100 1110 (16 бит).
· Открытый текст того же формата,
Например: Р = 1 5 6 11 = 0001 0101 0110 1011.
В приведенных арифметических выражениях вся арифметика в 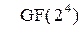 . Параметром задания является номер в списке группы i и номер группы k = 1 или 2 или 3. Многочлены
. Параметром задания является номер в списке группы i и номер группы k = 1 или 2 или 3. Многочлены 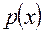 и
и 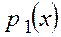 и
и 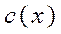 заданы в таблице 1 десятичными числами.
заданы в таблице 1 десятичными числами.
Ключ 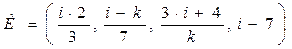 .
.
Открытый текст 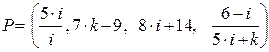 .
.
Задание начать с построения поля. Далее – сгенерировать цикловые ключи, вывести их на печать. Затем сгенерировать S - box и Mixcolumn и обратные к ним преобразования для всех элементов поля (в виде таблицы). Все шаги алгоритма оформить в виде двух состояний – вход-выход.
Задание 2.
В таблице 2 приведены открытые ключи собеседника по секретной переписке с помощью алгоритма RSA и его секретное зашифрованное сообщение. Требуется:
1. Выработать свои секретные ключи.
2. Расшифровать посланное секретное сообщение.
3. Выработать общий ключ для обеспечения секретности на основе открытого ключа.
4. Послать абоненту расшифрованное верифицированное сообщение (т.е. сообщение и его цифровая подпись)
Задание 3.
Открытый элемент Р задан в табл. 3 – графа 2. Найти примитивный элемент поля. Считая, что секретный ключ каждого участника равен номеру студента в списке группы i , вычислить ключ обмена для участника с номером 35 – i по алгоритму Диффи – Хэллмана
Задание 4
Зашифровать поговорку, выбранную из списка в соответствии с номером студента в группе различными спопобами:
1. спомощью способов, указанных в таблице3. графа 2;
2. С помощью ключа (пароля), где в качестве ключа используем:
1. константу с=3;
2. следующую в списке поговорку, используя алфавит Z33 = (А….Я, е=ё + пробел);
3. псевдослучайную последовательность, сгенерированную линейным рекуррентным генератором. Зашифровать 7 первых символов, используя алфавит Z32 и равномерный код. ПСП генерируется матрицей 5*5.
Полученное сообщение подписать, используя алгоритм Эль - Гамаля. В качестве хэш-функции использовать сумму пятиразрядных блоков по модулю 2
Примеры выполнения задания
Пример выполнения Задания1. Упрощенный алгоритм Rijndael,.
Построение поля
Вариант № 7, группа 2091 (№ 1)
Номер в списке группы i = 7
Номер группы k = 1
В приведенных арифметических выражениях вся арифметика в GF(24).
За неприводимый многочлен возьмем P(x) = x4+x+1.
Тогда за примитивный элемент можно взять a = x.
Элементы поля
| a | 0010 | 2 | x | a6 | 1100 | 12 | x3+x2 | a11 | 1110 | x3+x2+x | 14 |
| a2 | 0100 | 4 | x2 | a7 | 1011 | 11 | x3+x+1 | a12 | 1111 | x3+x2+x+1 | 15 |
| a3 | 1000 | 8 | x3 | a8 | 0101 | 5 | x2+1 | a13 | 1101 | x3+x2+1 | 13 |
| a4 | 0011 | 3 | x+1 | a9 | 1010 | 10 | x3+x | a14 | 1001 | x3+1 | 9 |
| a5 | 0110 | 6 | x2+x | a10 | 0111 | 7 | x2+x+1 | a15 | 0001 | 1 | 1 |
Обратные элементы
| a-1 | a14 | a-6 | a9 | a-11 | a4 |
| a-2 | a13 | a-7 | a8 | a-12 | a3 |
| a-3--3 | a12 | a-8 | a7 | a-13 | a2 |
| a-434 | a11 | a-9 | a6 | a-14 | a |
| a35-5 | a10 | a-10 | a5 | a-15 | a15 |
Многочлены для ByteSub
| № | P(x) | P1(x) | C(x) |
| 7 | 7 | 6 | 1, 13 |
p(x) = 710 = 01112 = x2 + x + 1 = a10
p1(x) = 610 = 01102 = x2 + x = a5
Многочлен для MixColumn
c(x) = x + 13 = 0001 * x + 1101
Ключ К
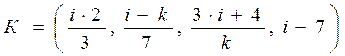
i * 2 / 3 = 7 * 2 / 3 = a10 * a * a-4 = a11 * a11 = a15 * a7 = a7 = 10112
(i – k) / 7 = (7 - 1) / 7 = (0111 + 0001) * a-10 = 0110 * a5 = a5 * a5 = a10 = 01112
(3 * i + 4) / k = (3 * 7 + 4) / 1 = (a4 * a10 + 0010) = a14 + 0010 = 1001 + 0010 = 10112
i – 7 = 7 – 7 = 0
K = (1011 0111 1011 0000)
Открытый текст P
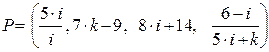
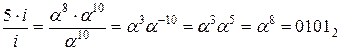
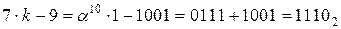
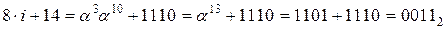
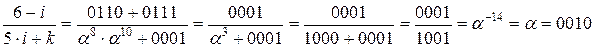
P = (0101 1110 0011 0010)
S преобразование и обратное для всех элементов
p(x) = 710 = 01112 = x2 + x + 1 = a10
p1(x) = 610 = 01102 = x2 + x = a5
S(x) = x-1 p + p1
S(0) = a5 = 0110
S(a) = a-1 a10 + a5 = a14 a10 + 0110 = a9 + 0110 = 1010 + 0110 = 1100
S(a2) = a-2 a10 + a5 = a13 a10 + 0110 = a8 + 0110 = 0101 + 0110 = 0011
S(a3) = a-3 a10 + a5 = a12 a10 + 0110 = a7 + 0110 = 1011 + 0110 = 1101
S(a4) = a-4 a10 + a5 = a11 a10 + 0110 = a6 + 0110 = 1100 + 0110 = 1010
S(a5) = a-5 a10 + a5 = a10 a10 + 0110 = a5 + 0110 = 0110 + 0110 = 0000
S(a6) = a-6 a10 + a5 = a9 a10 + 0110 = a4 + 0110 = 0011 + 0110 = 0101
S(a7) = a-7 a10 + a5 = a8 a10 + 0110 = a3 + 0110 = 1000 + 0110 = 1110
S(a8) = a-8 a10 + a5 = a7 a10 + 0110 = a2 + 0110 = 0100 + 0110 = 0010
S(a9) = a-9 a10 + a5 = a6 a10 + 0110 = a1 + 0110 = 0010 + 0110 = 0100
S(a10) = a-10 a10 + a5 = a5 a10 + 0110 = 0001 + 0110 = 0111
S(a11) = a-11 a10 + a5 = a4 a10 + 0110 = a14 + 0110 = 1001 + 0110 = 1111
S(a12) = a-12 a10 + a5 = a3 a10 + 0110 = a13 + 0110 = 1101 + 0110 = 1011
S(a13) = a-13 a10 + a5 = a2 a10 + 0110 = a12 + 0110 = 1111 + 0110 = 1001
S(a14) = a-14 a10 + a5 = a1 a10 + 0110 = a11 + 0110 = 1110 + 0110 = 1000
S(a15) = a-15 a10 + a5 = a15 a10 + 0110 = a10 + 0110 = 0111 + 0110 = 0001
Обратные преобразования
| S-1(0110) = 0 = 0000 S-1(1100) = a = 0010 S-1(0011) = a2 = 0100 S-1(1101) = a3 = 1000 S-1(1010) = a4 = 0011 S-1(0000) = a5 = 0110 S-1(0101) = a6 = 1100 S-1(1110) = a7 = 1011 | S-1(0010) = a8 = 0101 S-1(0100) = a9 = 1010 S-1(0111) = a10 = 0111 S-1(1111) = a11 = 1110 S-1(1011) = a12 = 1111 S-1(1001) = a13 = 1101 S-1(1000) = a14 = 1001 S-1(0001) = a15 = 0001 |
Шифрование
0) 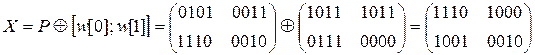
1.1) SubBytes
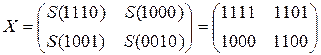
1.2) ShiftRow
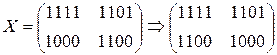
1.3) MixColumn
c(x) = x + 13 = 0001 * x + 1101
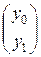 =
= 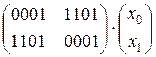
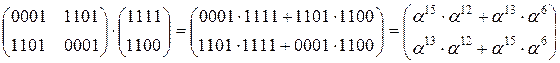 =
=
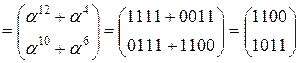
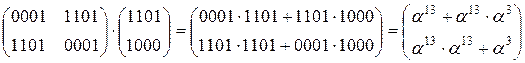 =
=
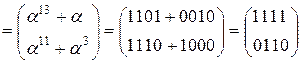
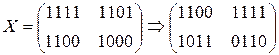
1.4) AddRoundKey
W[2] = 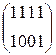 W[3] =
W[3] = 
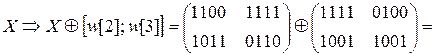
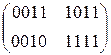
2.1) SubBytes
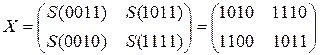
2.2) ShiftRow
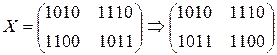
2.3) AddRoundKey
W[4] = 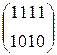 W[5] =
W[5] = 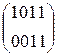
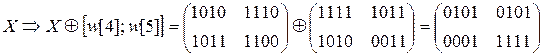
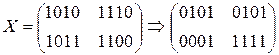
Зашифрованный текст
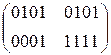 С = (5, 1, 5, 15)
С = (5, 1, 5, 15)
Расшифровка
0) x = x + k2
1.1) x = r -> (x)
1.2) x = s-1 (x)
1.3) x = x + k1
1.4) x = m-1 x
2.1) x = r -> (x)
2.2) x = s-1 (x)
2.3) x = x + k0
0) 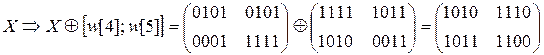
1.1) ShiftRow >
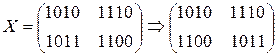
SubBytes
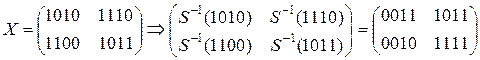
AddRoundKey
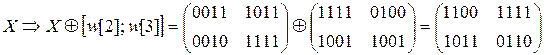
1.4) MixColumn
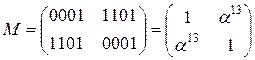
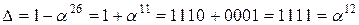
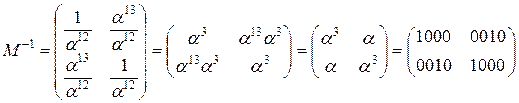
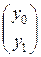 =
= 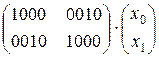
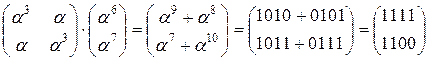
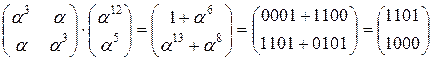
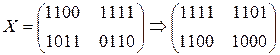
2.1) ShiftRow >
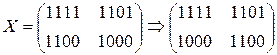
2.2) SubBytes
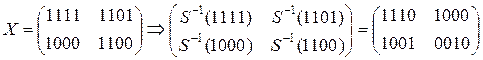
2.3) AddRoundKey
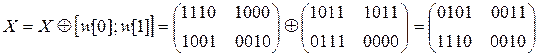
P = (0101 1110 0011 0010)
После шифровки и расшифровки был получен исходный открытый текст.
Пример выполнения Задания1. Упрощенный алгоритм Rijndael,.
ПОСТРОЕНИЕ ПОЛЯ
В приведенных арифметических выражениях вся арифметика в GF(24).
Неприводимый многочлен P(x) = x4+x+1.
Примитивный элемент a = x.
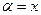
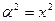
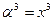
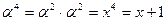
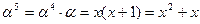
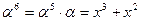
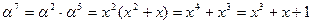
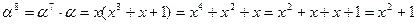
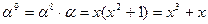
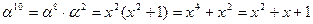
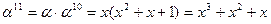
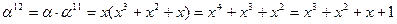
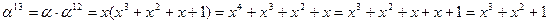
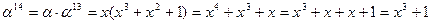
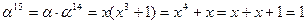
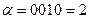
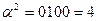
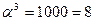
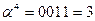
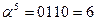
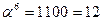
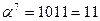
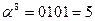
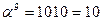
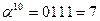
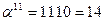
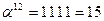
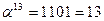
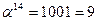
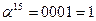
Обратные элементы:
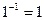
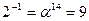
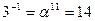
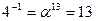
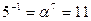
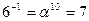
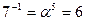
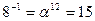
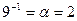
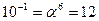
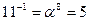
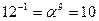
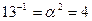
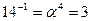
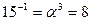
ПАРАМЕТРЫ АЛГОРИТМА
i = 15, k = 1
Многочлены для ByteSub :
p1(x) = 12 = 1100 = x3 + x2
p0(x) = 4 = 0100 = x2
Многочлен для MixColumn :
с(x) = 6x + 11 = 0110*x + 1011
Открытый ключ К:
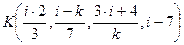
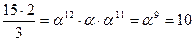
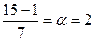
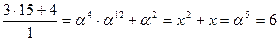
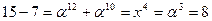
K = (10, 2, 6, 8)
| 1010 | 0110 |
| 0010 | 1000 |
Открытый текст:
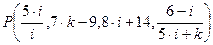
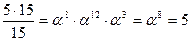
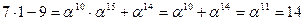
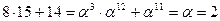
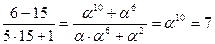
P = (5, 14, 2, 7)
| 0101 | 0010 |
| 1110 | 0111 |
S - box и обратное преобразование:
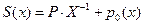
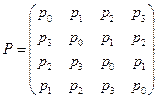 =
= 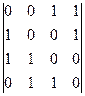
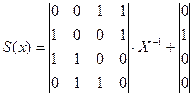

Обратное преобразование:
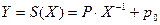 ;
;
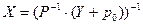 ;
;
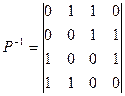 ; S -1:
; S -1: 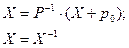
7
Матрица М:
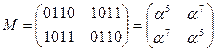
Матрица 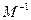 :
:
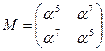
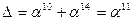
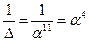
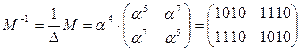
| x | x-1 | S(x) | S-1(x) | ||
| 0 | 0000 | 0 | 0000 | 0100 | 0010 |
| α | 0010 | 2 | 1001 | 1110 | 1111 |
| α2 | 0100 | 4 | 1101 | 1101 | 1001 |
| α3 | 1000 | 8 | 1111 | 0100 | 0011 |
| α4 | 0011 | 3 | 1110 | 1000 | 0001 |
| α5 | 0110 | 6 | 0111 | 0010 | 1111 |
| α6 | 1100 | 12 | 1010 | 1011 | 1110 |
| α7 | 1011 | 11 | 0101 | 1011 | 1100 |
| α8 | 0101 | 5 | 1011 | 0111 | 1110 |
| α9 | 1010 | 10 | 1100 | 0001 | 0111 |
| α10 | 0111 | 7 | 0110 | 1110 | 0101 |
| α11 | 1110 | 14 | 0011 | 0101 | 0010 |
| α12 | 1111 | 15 | 1000 | 0010 | 0010 |
| α13 | 1101 | 13 | 0100 | 0111 | 0100 |
| α14 | 1001 | 9 | 0010 | 1101 | 1010 |
| α15 | 0001 | 1 | 0001 | 1000 | 1010 |
ШИФРОВАНИЕ
· 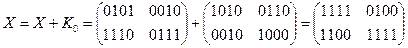
· 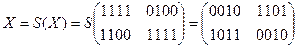
· 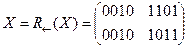
· 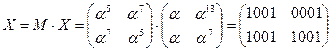
· 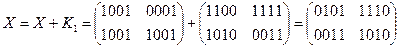
· 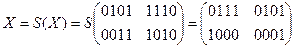
· 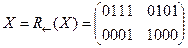
· 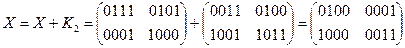
Зашифрованный текст: 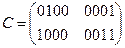
ДЕШИФРОВАНИЕ
· 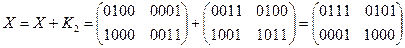
· 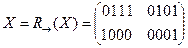
· 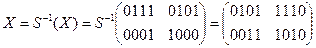
· 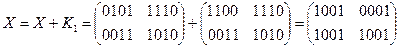
· 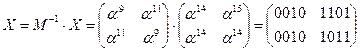
· 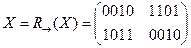
· 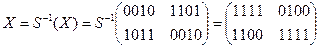
· 
Расшифрованный текст 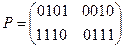 соответствует исходному.
соответствует исходному.
Пример выполнения Задания2. .
Алгоритм шифрования RSA. Цифровая подпись
Группа 2091, вариант №7.
|
| открытый ключ | шифро- текст | |
| № | n=p*q | e | c |
| 7 | |||
667
17
219
Расшифровать текст C = 219.
Открытый ключ n = p*q = 667.
e = 17
Подбираем простые числа p и q. Получаем следующее представление n:
n = p*q = 667 = 23 * 29.
Найдем значение функции Эйлера:
j(n) = (p-1)(q-1) = 22*28 = 616.
В соответствии с алгоритмом шифрования RSA число е выбирается так, чтобы значения j(n) и e были взаимно простыми. Числа 638 и 17 являются взаимно простыми: у них нет общего делителя кроме единицы. Таким образом, число e выбрано корректно.
(638, 17) = 1
Чтобы расшифровать сообщение, необходимо найти секретный ключ d. Для этого нужно решить сравнение I степени:
ed º 1 mod j(n)
17d º 1 mod 616
Для решения сравнения воспользуемся алгоритмом Евклида:
17 = 616*0 +17
616 = 17*36 + 4
17 = 4*4 + 1
4 = 1*4 + 0
| n | -2 | -1 | 0 | 1 | 2 | 3 |
| qn | 0 | 36 | 4 | 4 | ||
| Pn | 0 | 1 | - | - | - | - |
| Qn | 1 | 0 | 1 | 36 | 145 | - |
d = (-1)k-1Qk-1 mod j(n) = 145 mod 616 = 145
Дешифрование
Открытый текст M = Cd mod n
M = 219145 mod 667 = 52
Открытый текст M = 52.
Шифрование
C = Me mod 667 = 5217 mod 667 = 219
Подпись
Открытый ключ e = 17
Открытый ключ n = 667
Секретный ключ d = 145
Возвести открытый текст (его хэш) в степень d по модулю n, получаем подпись.
sign = 52 ^ 145 mod 667 = 634
Проверка подписи
Получатель получает сообщение с подписью, подпись возводит в степень e по модулю n.
634 ^ 17 mod 667 = 52
При проверке получено сообщение (хэш сообщения), следовательно верификация сообщения пройдена успешно.
Пример выполнения Задания2
Алгоритм шифрования RSA. Цифровая подпись
Пример выполнения Задания3.
Алгоритм Диффи-Хеллмана
Открытый элемент Р задан в таблице 3 – графа 2. Найти примитивный элемент поля. Считая, что секретный ключ каждого участника равен номеру студента в списке группы i , вычислить ключ обмена для участника с номером 35 – i по алгоритму Диффи-Хэллмана.
Вариант № 7, группа 2091 (№ 1)
Номер в списке группы i = 7
Номер группы k = 1
P = 43
Открытый элемент P = 43. Найти примитивный элемент поля. Секретный ключ каждого участника i = 7, вычислить ключ обмена для участника с номером 35.
GF(43) = <0, 1, 2, 3, …, 40, 41, 42>
Найдем примитивный элемент поля GF(43).
Требуется найти такое число, принадлежащее интервалу [2,42], которое при возведении в 42-ю степень по модулю 43 будет давать в результате единицу. Если же единица будет получена раньше, чем при возведении в 42-ю степень, результаты возведения в степень начнут повторяться, и через выбранный элемент не удастся представить все элементы поля. Исходя из таких соображений, получаем несложный алгоритм нахождения примитивных элементов поля GF(43).
Алгоритм нахождения примитивных элементов поля GF(43).
int _tmain(int argc, _TCHAR* argv[])
{
long int mem, i, j, num, deg, modul, res;
unsigned char mas[44];
deg = 0; modul = 43; mem = 2;
while (mem < 42)
{
num = mem; deg = 0;
while (deg != 42)
{
res = 1; deg = 0;
for (i = 0; i < 42; i++) mas[i] = 0;
do
{
res = res*num; res = res % modul;
deg++; mas[deg] = res;
}
while(res != 1);
num++;
}
std::cout << num-1 << std::endl;
for (i = 0; i < 42; i++)
{
for (j = 0; j < 42; j++)
{
if ((i != j) && (mas[j] == mas[i]))
std::cout << "Wrong" << std::endl;
}
mem = num;
}
}
return 0;
}
В результате выполнения программы получим следующие значения:
3, 5, 12, 18, 19, 20, 26, 28, 29, 30, 33, 34
Выберем значение α = 20. Найдем элементы поля.
| α = 20 α2 = 13 α3 = 2 α4 = 40 α5 = 26 α6 = 4 α7 = 37 α8 = 9 α9 = 8 α10 = 31 α11 = 18 | α12 = 16 α13 = 19 α14 = 36 α15 = 32 α16 = 38 α17 = 29 α18 = 21 α19 = 33 α20 = 15 α21 = 42 α22 = 23 | α23 = 30 α24 = 41 α25 = 3 α26 = 17 α27 = 39 α28 = 6 α29 = 34 α30 = 35 α31 = 12 α32 = 25 α33 = 27 | α34 = 24 α35 = 7 α36 = 11 α37 = 5 α38 = 14 α39 = 22 α40 = 10 α41 = 28 α42 = 1 |
Секретный ключ участника А: XA = 7.
Секретный ключ участника B: YB = 35-7 = 28.
Открытый ключ участника А: 
Открытый ключ участника B: 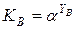
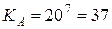
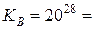 15 * 208 = 6
15 * 208 = 6
Обменный ключ участника А: 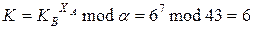
Обменный ключ участника B: 
Значения обменного ключа для А и В совпадают.
Обменный ключ: K = 6
Пример выполнения Задания3. Алгоритм Диффи-Хеллмана
Открытый элемент Р задан в таблице 3 – графа 2. Найти примитивный элемент поля. Считая, что секретный ключ каждого участника равен номеру студента в списке группы i , вычислить ключ обмена для участника с номером 35 – i по алгоритму Диффи-Хэллмана.
Вариант № 15, группа 2091 (№ 1)
Номер в списке группы i = 15
Номер группы k = 1
P = 37
Открытый элемент P = 37. Найти примитивный элемент поля. Секретный ключ каждого участника i = 15, вычислить ключ обмена для участника с номером 35-15 = 20.
GF(37) = <0, 1, 2, 3, …, 35, 36, 37>
Найдем примитивный элемент поля GF(37).
Требуется найти такое число, принадлежащее интервалу [2,37], которое при возведении в 37-ю степень по модулю 37 будет давать в результате единицу. Если же единица будет получена раньше, чем при возведении в 36-ю степень, результаты возведения в степень начнут повторяться, и через выбранный элемент не удастся представить все элементы поля. Исходя из таких соображений, получаем несложный алгоритм нахождения примитивных элементов поля GF(37).
Алгоритм нахождения примитивных элементов поля GF(37).
int _tmain(int argc, _TCHAR* argv[])
{
long int mem, i, j, num, deg, modul, res;
unsigned char mas[38];
deg = 0; modul = 37; mem = 2;
while (mem < 36)
{
num = mem; deg = 0;
while (deg != 36)
{
res = 1; deg = 0;
for (i = 0; i < 36; i++) mas[i] = 0;
do
{
res = res*num; res = res % modul;
deg++; mas[deg] = res;
}
while(res != 1);
num++;
}
std::cout << num-1 << std::endl;
for (i = 0; i < 36; i++)
{
for (j = 0; j < 36; j++)
{
if ((i != j) && (mas[j] == mas[i]))
std::cout << "Wrong" << std::endl;
}
mem = num;
}
}
}
В результате выполнения программы получим следующие значения:
2, 5, 13, 15, 17, 18, 19, 20, 22, 24, 32, 35
Выберем значение α = 2.
Секретный ключ участника А: XA = 15.
Секретный ключ участника B: YB = 35-15 = 20.
Открытый ключ участника А: 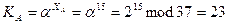
Открытый ключ участника B: 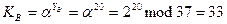

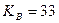
Обменный ключ участника А: 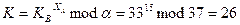
Обменный ключ участника B: 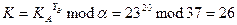
Значения обменного ключа для А и В совпадают.
Обменный ключ: K = 26
Пример выполнения Задания4. Традиционное шифрование
Вариант № 7, группа 2091 (№ 1)
Номер в списке группы i = 7
Номер группы k = 1
| № | P | Открытый текст | способ |
| 7 | 43 | Повадки волчьи, а душа заячья | Хилла, цифирь Петра 1 |
Задание
Зашифровать поговорку, выбранную из списка в соответствии с номером студента в группе:
1. С помощью способов, указанных в таблице
2. С помощью ключа, где в качестве ключа используем
a. константу c = 3
b. следующую в списке поговорку, используя алфавит
Z33 = (А….Я, е=ё + пробел).
c. псевдослучайную последовательность, сгенерированную линейным рекуррентным генератором. Зашифровать 7 первых символов, используя алфавит Z32 и равномерный код. ПСП (псевдослучайная последовательность) генерируется матрицей 5*5.
Полученное сообщение подписать, используя алгоритм Эль-Гамаля. В качестве хэш-функции использовать сумму пятиразрядных блоков по модулю 2.
1.1 Цифирь Петра Первого (аналог)
| а | б | в | г | д | е | ё | ж | з | и | й |
| я | ты | они | она | от | кому | ему | им | сейчас | потом | иногда |
| к | л | м | н | о | п | р | с | т | у | ф |
| когда | всегда | часто | редко | метко | редко | криво | прямо | мы | нам | налево |
| х | ц | ч | ш | щ | ъ | ы | ь | э | ю | я |
| направо | вперед | назад | вбок | вниз | вверх | бегом | шагом | быстро | четко | туда |
Повадки волчьи, а душа заячья
Жирным шрифтом выделены фрагменты, которые не несут смысловой нагрузки в шифре. Остальной текст может быть расшифрован согласно таблице выше.
редко но метко они или я и от меня но когда лето потом зима
они метко всегда назад стреляли шагом потом уходили
я пришел
от нам повезло вбок я получил
сейчас я туда назад шагом снова туда пойду
Способ Хилла
Будем использовать следующий алфавит.
| а | б | в | г | д | е | ж | з | и | й | к |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| л | м | н | о | п | р | с | т | у | ф | х |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| ц | ч | ш | щ | ъ | ы | ь | э | ю | я | _ |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
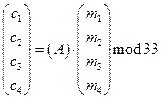 Пусть
Пусть 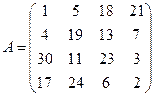
Например:
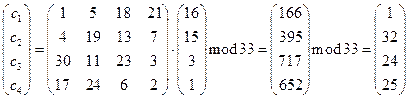
Разобьем поговорку на блоки по четыре буквы:
| ПОВА | ДКИ_ | ВОЛЧ | ЬИ_А | _ДУШ | А_ЗА | ЯЧЬЯ |
| (16 15 3 1) | (5 11 9 33) | (3 15 12 24) | (27 9 33 1) | (33 5 20 25) | (1 33 8 1) | (32 24 27 32) |
| (1 32 24 25) | (24 16 16 7) | (6 27 9 3) | (27 22 21 17) | (19 2 29 26) | (1 16 18 1) | (23 4 27 26) |
| АЯЧШ | ЧППЖ | ЕЬИВ | ЬХФР | ТБЪЩ | АПТА | ЦГЬЩ |
Итак, после преобразования по методу Хилла, получаем:
ПОВАДКИ_ВОЛЧЬИ_А_ДУША_ЗАЯЧЬЯ = АЯЧШЧППЖЕЬИВЬХФРТБЪЩАПТАЦГЬЩ
Шифрование с помощью пароля
c = 3
Алфавит
абвгдеёжзийклмнопрстуфхцчшщъыьэюя_
Исходный текст:
Повадки_волчьи,_а_душа_заячья
После шифрования получим:
Тсегжнлвесоьэл,вгвжцыгвкгбьэб
С помощью текста
В качестве пароля взять следующую в списке поговорку.
Пароль:
По хозяину и собаке честь
Алфавит
Z33 = (А….Я, е=ё + пробел).
абвгдежзи й к л м н о п р с т у ф х ц ч ш щ ъ ы ь э ю я _
012345678 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
Пароль
По_хозяину_и_собаке_честьПо_хозяину и собаке честь
Исходный текст:
Повадки_волчьи_а_душа_заячья
Зашифрованный текст:
Юьбхтсжзпакяыщнб_ошччдштъейю
Расчеты:
п + п = (15 + 15) mod 33 = 30 = ю
о + о = (14 + 14) mod 33 = 28 = ь
_ + в = (32 + 2) mod 33 = 1 = б
х + а = (21 + 0) mod 33 = 21 = х
о + д = (14 + 4) mod 33 = 18 = т
з + к = (7 + 10) mod 33 = 17 = с
я + и = (31 + 8) mod 33 = 6 = ж
и + _ = (8 + 32) mod 33 = 7 = з
н + в = (13 + 2) mod 33 = 15 = п
у + о = (19 + 14) mod 33 = 0 = а
_ + л = (32 + 11) mod 33 = 10 = к
и + ч = (8 + 23) mod 33 = 31 = я
_ + ь = (32 + 28) mod 33 = 27 = ы
с + и = (17 + 8) mod 33 = 25 = щ
о + _ = (14 + 32) mod 33 = 13 = н
а + б = (0 + 1) mod 33 = 1 = б
а + _ = (0 + 32) mod 33 = 32 = _
к + д = (10 + 4) mod 33 = 14 = о
е + у = (5 + 19) mod 33 = 24 = ш
_ + ш = (32 + 24) mod 33 = 23 = ч
ч + а = (23 + 0) mod 33 = 23 = ч
е + _ = (5 + 32) mod 33 = 4 = д
с + з = (17+ 7) mod 33 = 24 = ш
т + а = т
ь + я = (28+ 31) mod 33 = 26 = ъ
п + ч = (15+ 23) mod 33 = 5 = е
о + ь = (14 + 28) mod 33 = 9 = й
_ + я = ю
После шифрования получаем:
Юьбхтсжзпакяыщнб_ошччдштъейю
Подпись сообщения
Запишем полученное сообщение в виде матрицы:
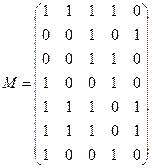 ;
;
Подпишем полученное сообщение М. Возьмем p=23 и примитивный элемент поля GF(23) g=5, выберем xa=5, тогда открытый ключ 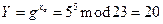 .
.
Значение хэш-функции:
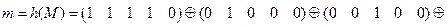
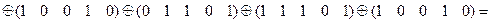
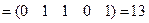 ;
;
Возьмем случайное число k= 3;
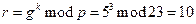 ;
; 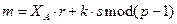 ;
;
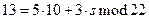
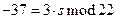
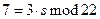
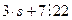
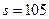
Проверим полученную подпись:
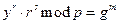
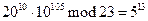
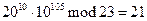
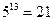
Итак, получим цифровую подпись сообщения (r,s) = (10, 105)=(10, 9)=(Л, К).
отправить нужно сообщение ЯЕЖУОЮУЛК.
С помощью способов, указанных в таблице требуется зашифровать поговорку: «Не пойман не вор не уличена не гулена».
4 Тарабарская грамота.
| Б | - | Щ | З | - | Ф | |
| В | - | Ш | К | - | Т | |
| Г | - | Ч | Л | - | С | |
| Д | - | Ц | М | - | Р | |
| Ж | - | Х | Н | - | П |
| Исходный текст | Не пойман не вор не уличена не гулена |
| Шифрованный текст | Пе нойрап пе шом пе усигепа пе чусепа |
5 Шифрование с помощью ключа:
5.1 ключ к онстанта С=3.
| А | (0+3)(mod 32)=3 | Г |
| Б | (1+3)(mod 32)=4 | Д |
| В | (2+3)(mod 32)=5 | Е |
| Г | (3+3)(mod 32)=6 | Ж |
| Д | (4+3)(mod 32)=7 | З |
| Е | (5+3)(mod 32)=8 | И |
| Ж | (6+3)(mod 32)=9 | Й |
| З | (7+3)(mod 32)=10 | К |
| И | (8+3)(mod 32)=11 | Л |
| Й | (9+3)(mod 32)=12 | М |
| К | (10+3)(mod 32)=13 | Н |
| Л | (11+3)(mod 32)=14 | О |
| М | (12+3)(mod 32)=15 | П |
| Н | (13+3)(mod 32)=16 | Р |
| О | (14+3)(mod 32)=17 | С |
| П | (15+3)(mod 32)=18 | Т |
| Р | (16+3)(mod 32)=19 | У |
| С | (17+3)(mod 32)=20 | Ф |
| Т | (18+3)(mod 32)=21 | Х |
| У | (19+3)(mod 32)=22 | Ц |
| Ф | (20+3)(mod 32)=23 | Ч |
| Х | (21+3)(mod 32)=24 | Ш |
| Ц | (22+3)(mod 32)=25 | Щ |
| Ч | (23+3)(mod 32)=26 | Ь |
| Ш | (24+3)(mod 32)=27 | Ы |
| Щ | (25+3)(mod 32)=28 | Ъ |
| Ь | (26+3)(mod 32)=29 | Э |
| Ы | (27+3)(mod 32)=30 | Ю |
| Ъ | (28+3)(mod 32)=31 | Я |
| Э | (29+3)(mod 32)=0 | A |
| Ю | (30+3)(mod 32)=1 | Б |
| Я | (31+3)(mod 32)=2 | В |
| Исходный текст | НЕПОЙМАННЕВОРНЕУЛИЧЕНАНЕГУЛЕНА |
| Шифрованный текст | РИТСМПГРРИЕСУРИЦОЛЬИРГРИЖЦОИРГ |
5.2. С помощью ключа К=НЕ РОБЕЙ ВОРОБЕЙ ДЕРЖИСЬ ОРЛОМ
| Н | Е | П | О | Й | М | А | Н | Н | Е | В | О | Р | Н | Е | ||||
| 13 | 5 | 32 | 15 | 14 | 9 | 12 | 0 | 13 | 32 | 13 | 5 | 32 | 2 | 14 | 16 | 32 | 13 | 5 |
| Н | Е | Р | О | Б | Е | Й | В | О | Р | О | Б | Е | Й | Д | Е | |||
| 13 | 5 | 32 | 16 | 14 | 1 | 5 | 9 | 32 | 2 | 14 | 16 | 14 | 1 | 5 | 9 | 32 | 4 | 5 |
| 26 | 10 | 31 | 31 | 28 | 10 | 17 | 9 | 12 | 1 | 27 | 21 | 13 | 3 | 19 | 25 | 31 | 17 | 10 |
| Ь | К | Я | Я | Ъ | К | С | Й | М | Б | Ы | Х | Н | Г | У | Щ | Я | С | К |
| У | Л | И | Ч | Е | Н | А | Н | Е | Г | У | Л | Е | Н | А | ||||
| 32 | 19 | 11 | 8 | 23 | 5 | 13 | 0 | 32 | 13 | 5 | 32 | 3 | 19 | 11 | 5 | 13 | 0 | |
| Р | Ж | И | С | Ь | О | Р | Л | О | М | Н | Е | Р | О | Б | Е | |||
| 16 | 6 | 8 | 17 | 26 | 32 | 14 | 16 | 11 | 14 | 12 | 13 | 5 | 32 | 16 | 14 | 1 | 5 | |
| 15 | 25 | 19 | 25 | 16 | 4 | 27 | 16 | 10 | 27 | 17 | 12 | 8 | 18 | 27 | 19 | 14 | 5 | |
| П | Щ | У | Щ | Р | Д | Ы | Р | К | Ы | С | М | И | Т | Ы | У | О | Е |
| Исходный текст | НЕ ПОЙМАН НЕ ВОР НЕ УЛИЧЕНА НЕ ГУЛЕНА |
| Шифрованный текст | ЬКЯЯЪКСЙМБЫХНГУЩЯСКПЩУЩРДЫРКЫСМИТЫУОЕ |
Шифрование с помощью ПСП.
Поле 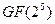 .
. 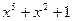 - примитивный многочлен.
- примитивный многочлен.
Матрица, соответствующая примитивному многочлену: 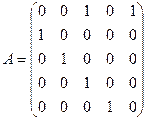 .
.
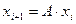 ;
;
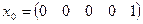 ;
; 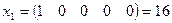 ;
;
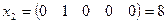 ;
; 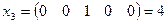 ;
;
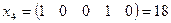 ;
; 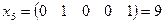 ;
;
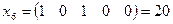 ;
; 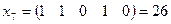 ;
;
| Н | Е | П | О | Й | М | |
| 13 | 5 | 32 | 15 | 14 | 9 | 12 |
| 16 | 8 | 4 | 18 | 9 | 20 | 26 |
| 29 | 13 | 3 | 0 | 25 | 29 | 5 |
| Э | Н | Г | А | Щ | Э | Е |
| 11101 | 01101 | 00011 | 00000 | 11001 | 11101 | 00101 |
| Исходный текст | НЕ ПОЙМ |
| Шифрованный текст | ЭНГАЩЭЕ |
Метод Хилла
Зашифровать поговорку «сухой по мокрому не тужит».
| А | 1 |
| Б | 2 |
| В | 3 |
| Г | 4 |
| Д | 5 |
| Е | 6 |
| Ж | 7 |
| З | 8 |
| И | 9 |
| Й | 10 |
| К | 11 |
| Л | 12 |
| М | 13 |
| Н | 14 |
| О | 15 |
| П | 16 |
| Р | 17 |
| С | 18 |
| Т | 19 |
| У | 20 |
| Ф | 21 |
| Х | 22 |
| Ц | 23 |
| Ч | 24 |
| Ш | 25 |
| Щ | 26 |
| Ь | 27 |
| Ы | 28 |
| Ъ | 29 |
| Э | 30 |
| Ю | 31 |
| Я | 32 |
| _ | 33 |
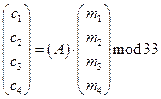 ;
;
Пусть 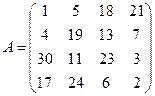 ;
;
Пример: 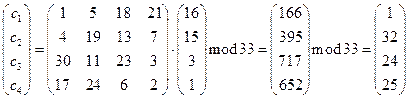
Разобьем поговорку на блоки по 4 буквы:
| СУХО | Й_ПО | МОКР | ОМУ_ | НЕ_Т | УЖИТ |
| (18 20 22 15) | (10 33 16 15) | (13 15 11 17) | (15 13 20 33) | (14 6 33 19) | (20 7 9 19) |
| (4 18 24 24) | (19 23 20 32) | (16 5 1 21) | (11 6 30 27) | (14 6 15 24) | (22 1 17 6) |
| ГСЧЧ | ТЦУЯ | ПДАФ | КЕЭЬ | НЕОЧ | ХАРЕ |
Итак, после преобразования по методу Хилла:
СУХОЙ_ПО_МОКРОМУ_НЕ_ТУЖИТ = ГСЧЧТЦУЯПДАФКЕЭЬНЕОЧХАРЕ
Цифирь Петра Первого
| А | ИР |
| Б | ГО |
| В | МО |
| Г | НЕ |
| Д | ЖЕ |
| Е | БЕ |
| Ж | РУ |
| З | КА |
| И | РА |
| Й | НД |
| К | АШ |
| Л | ТЕ |
| М | ЛЕ |
| Н | ДИ |
| О | ОК |
| П | ОМ |
| Р | ПА |
| С | НИ |
| Т | МА |
| У | РШ |
| Ф | ТК |
| Х | КИ |
| Ц | ТА |
| Ч | РО |
| Ш | СС |
| Щ | ИЯ |
| Ь | ГЫ |
| Ы | ВЬ |
| Ъ | СЭ |
| Э | ЮК |
| Ю | ЮЯ |
| Я | ЭМ |
| _ | ФУ |
СУХОЙ_ПО_МОКРОМУ_НЕ_ТУЖИТ = НИРШКИОКНДФУОМОКФУЛЕОКПАОКЛЕРШФУДИБЕФУМАРШРУРАМА
8 Шифрование с помощью ключа.
8.1 Ключ С = 3
С: (18+3) mod 33 = 21
У: (20+3) mod 33 = 23
Х: (22+3) mod 33 = 25
О: (15+3) mod 33 = 18
Й: (10+3) mod 33 = 13
_: (33+3) mod 33 = 3
П: (16+3) mod 33 = 19
М: (13+3) mod 33 = 16
К: (11+3) mod 33 = 14
Р: (17+3) mod 33 = 20
Н: (14+3) mod 33 = 17
Е: (6+3) mod 33 = 9
Т: (19+3) mod 33 = 21
Ж: (7+3) mod 33 = 10
И: (9+3) mod 33 = 12
СУХОЙ_ПО_МОКРОМУ_НЕ_ТУЖИТ = ФЦШСМВТСВПСНУСПЦВРИВХЦЙЛХ
8.1 2 Ключ = «Пуст мешок стоять не будет»
| P | K | C | ||||||
| А | 0 | 00000 | С | 10000 | П | 01110 | 11110 | Я |
| Б | 1 | 00001 | У | 10010 | У | 10010 | 00000 | А |
| В | 2 | 00010 | Х | 10100 | С | 10000 | 00100 | Д |
| Г | 3 | 00011 | О | 01101 | Т | 10001 | 11100 | Э |
| Д | 4 | 00100 | Й | 01000 | _ | 11111 | 10111 | Ш |
| Е | 5 | 00101 | _ | 11111 | М | 01011 | 10100 | Х |
| Ж | 6 | 00110 | П | 01110 | Е | 00101 | 01011 | М |
| З | 7 | 00111 | О | 01101 | Ш | 10111 | 11010 | Ы |
| И | 8 | 01000 | _ | 11111 | О | 01101 | 10010 | У |
| К | 9 | 01001 | М | 01011 | К | 01001 | 00010 | В |
| Л | 10 | 01010 | О | 01101 | _ | 11111 | 10010 | У |
| М | 11 | 01011 | К | 01001 | С | 10000 | 11001 | Ъ |
| Н | 12 | 01100 | Р | 01111 | Т | 10001 | 11110 | Я |
| О | 13 | 01101 | О | 01101 | О | 01101 | 00000 | А |
| П | 14 | 01110 | М | 01011 | Я | 11110 | 10101 | Ц |
| Р | 15 | 01111 | У | 10010 | Т | 10001 | 00011 | Г |
| С | 16 | 10000 | _ | 11111 | Ь | 11011 | 00100 | Д |
| Т | 17 | 10001 | Н | 01100 | _ | 11111 | 10011 | Ф |
| У | 18 | 10010 | Е | 00101 | Н | 01100 | 01001 | К |
| Ф | 19 | 10011 | _ | 11111 | Е | 00101 | 11010 | Ы |
| Х | 20 | 10100 | Т | 10001 | _ | 11111 | 01110 | П |
| Ц | 21 | 10101 | У | 10010 | Б | 00001 | 10011 | Ф |
| Ч | 22 | 10110 | Ж | 00110 | У | 10010 | 10100 | Х |
| Ш | 23 | 10111 | И | 01000 | Д | 00100 | 01100 | Н |
| Щ | 24 | 11000 | Т | 10001 | Е | 00101 | 10100 | Х |
| Ъ | 25 | 11001 | ||||||
| Ы | 26 | 11010 | ||||||
| Ь | 27 | 11011 | ||||||
| Э | 28 | 11100 | ||||||
| Ю | 29 | 11101 | ||||||
| Я | 30 | 11110 | ||||||
| _ | 31 | 11111 |
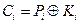 ;
;
СУХОЙ_ПО_МОКРОМУ_НЕ_ТУЖИТ = ЯАДЭШХМЫУВУЪЯАЦГДФКЫПФХНХ
ПРИЛОЖЕНИЕ
Табл.1 Выбор полиномов для
Задания 1.
| № В списке № | P ( x ) | P 1 ( x ) | C ( x ) |
| 1 | 10 | 6 | 4,6 |
| 2 | 11 | 5 | 7,3 |
| 3 | 12 | 4 | 5,8 |
| 4 | 13 | 3 | 11,2 |
| 5 | 14 | 2 | 13,4 |
| 6 | 15 | 1 | 6,2 |
| 7 | 7 | 6 | 1,13 |
| 8 | 11 | 5 | 5,6 |
| 9 | 12 | 4 | 11,3 |
| 10 | 13 | 3 | 14,6 |
| 11 | 14 | 2 | 2,9 |
| 12 | 6 | 1 | 5,10 |
| 13 | 10 | 6 | 3,7 |
| 14 | 11 | 5 | 8,6 |
| 15 | 12 | 4 | 6,11 |
| 16 | 13 | 3 | 1,5 |
| 17 | 14 | 2 | 8,5 |
| 18 | 9 | 1 | 2,4 |
| 19 | 10 | 6 | 8,3 |
| 20 | 11 | 5 | 4,2 |
| 21 | 12 | 4 | 8,1 |
| 22 | 13 | 3 | 2,6 |
| 23 | 14 | 2 | 5,7 |
| 24 | 7 | 1 | 5,11 |
| 25 | 7 | 6 | 3,8 |
| 26 | 12 | 3 | 13,4 |
| 27 | 9 | 6 | 6,2 |
Если P(x) задан неверно – (проверить!), то для четных № P(x) =13, для нечетных P(x) =7 .
Табл.2. Выбор параметров
для задания 2
|
№
| открытый ключ | шифро- текст | |
| В списке
| n=p*q | e | c |
| 1 | 473 | 17 | 471 |
| 2 | 481 | 19 | 359 |
| 3 | 493 | 13 | 263 |
| 4 | 589 | 19 | 244 |
| 5 | 437 | 17 | 383 |
| 6 | 1073 | 13 | 342 |
| 7 | 667 | 17 | 219 |
| 8 | 377 | 35 | 148 |
| 9 | 899 | 19 | 675 |
| 10 | 551 | 13 | 174 |
| 11 | 473 | 19 | 419 |
| 12 | 481 | 5 | 133 |
| 13 | 493 | 55 | 355 |
| 14 | 589 | 77 | 445 |
| 15 | 437 | 65 | 158 |
| 16 | 1073 | 99 | 149 |
| 17 | 667 | 65 | 464 |
| 18 | 377 | 55 | 14 |
| 19 | 899 | 29 | 316 |
| 20 | 551 | 31 | 23 |
| 21 | 473 | 43 | 401 |
| 22 | 481 | 47 | 52 |
| 23 | 493 | 47 | 280 |
| 24 | 493 | 61 | 84 |
| 25 | 437 | 53 | 244 |
| 26 | 1073 | 37 | 174 |
| 27 | 667 | 31 | 67 |
Таблица 3. Выбор параметров для задания 4
| № | P | Открытый текст | способ |
| 1 | 37 | Не пойман – не вор, не уличена – не гулёна. | Вижинера, тарабарская грамота |
| 2 | 23 | Не робей, воробей, держись орлом. | Маршрут.транспозиция, Плейфейера. |
| 3 | 29 | Не разводи усок на чужой кусок | Хилла, цифирь Петра 1 |
| 4 | 31 | Сурьма косых глаз не исправит. | Парный шифр, Гронфельда |
| 5 | 41 | сухой по мокрому не тужит. | Вижинера, тарабарская грамота |
| 6 | 22 | Повадится овца не хуже козы. | Маршрут.транспозиция, Плейфейера. |
| 7 | 43 | Повадки волчьи, а душа заячья | Хилла, цифирь Петра 1 |
| 8 | 37 | По хозяину и собаке честь. | Парный шифр, Гронфельда |
| 9 | 23 | Поздно щуке на сковороде вспоминать о воде. | Вижинера, тарабарская грамота |
| 10 | 29 | Поле глазасто, а лес ушаст. | Маршрут.транспозиция, Плейфейера |
| 11 | 31 | Порозно думать вместе не жить | Хилла, цифирь Петра 1 |
| 12 | 41 | Посуленному только дурак рад. | Парный шифр, Гронфельда |
| 13 | 23 | промеж худых и хорошему плохо.. | Вижинера, тарабарская грамота |
| 14 | 43 | Проживет Фаддей и без затей | Маршрут.транспозиция, Плейфейера |
| л15 | 37 | сухой по мокрому не тужит. | Хилла, цифирь Петра 1 |
| 16 | 23 | Пуст мешок стоять не будет. | Парный шифр, Гронфельда |
| 17 | 29 | Под каждой крышей свои мыши | Вижинера, тарабарская грамота |
| 18 | 31 | Пустой колос голову кверху носит. | Маршрут.транспозиция, Плейфейера |
| 19 | 41 | Родной куст и зайцу дорог. | Хилла, цифирь Петра 1 |
| 20 | 29 | Спесь росту не прибавит. | Парный шифр, Гронфельда |
| 21 | 43 | Не пойман-не вор, не уличена - не гулёна. | Вижинера, тарабарская грамота |
| 22 | 37 | Не робей, воробей, держись орлом. | Маршрут.транспозиция, Плейфейера |
| 23 | 23 | Не разводи усок на чужой кусок | Хилла, цифирь Петра 1 |
| 24 | 29 | Сурьма косых глаз не исправит. | Парный шифр, Гронфельда |
| 25 | 31 | сухой по мокрому не тужит. | Вижинера, тарабарская грамота |
| 26 | 41 | Повадится овца не хуже козы. | Маршрут.транспозиция, Плейфейера |
| 27 | 37 | Повадки волчьи, а душа заячья | Хилла, цифирь Петра 1 |
| 28 | 43 | По хозяину и собаке честь. | Парный шифр, Гронфельда |
| 29 | 31 | Поздно щуке на сковороде вспоминать о воде. | Вижинера, тарабарская грамота |
Задания на лабораторные работы
Задание 1
Зашифровать и расшифровать открытый текст с помощью упрощенного алгоритма VS-AES. Выполнить 2 итерации. Параметрами алгоритма являются:
· Многочлены для ByteSub :
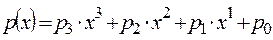 и
и 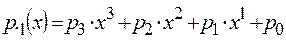
· с коэффициентами из GF(2), которые можно задать двоичным вектором.
Например, многочлен 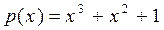 можно задать двоичным вектором (1 1 0 1) или десятичным числом “13 ”, соответствующим этому вектору.
можно задать двоичным вектором (1 1 0 1) или десятичным числом “13 ”, соответствующим этому вектору.
· Многочлен первой степени для MixColumn c коэффициентами из 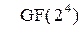
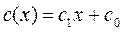 , задаваемый двумя числами из
, задаваемый двумя числами из 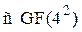 .
.
Например, пара чисел (3.8) соответствует многочлену
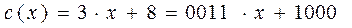
· Ключ К, состоящий из четырех полубайтов, выраженных десятичными числами.
Например, К = 12 1 4 14 = 1100 0001 0100 1110 (16 бит).
· Открытый текст того же формата,
Например: Р = 1 5 6 11 = 0001 0101 0110 1011.
В приведенных арифметических выражениях вся арифметика в 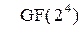 . Параметром задания является номер в списке группы i и номер группы k = 1 или 2 или 3. Многочлены
. Параметром задания является номер в списке группы i и номер группы k = 1 или 2 или 3. Многочлены 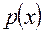 и
и 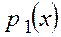 и
и 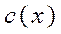 заданы в таблице 1 десятичными числами.
заданы в таблице 1 десятичными числами.
Ключ 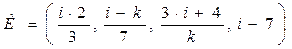 .
.
Открытый текст 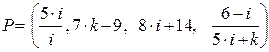 .
.
Задание начать с построения поля. Далее – сгенерировать цикловые ключи, вывести их на печать. Затем сгенерировать S - box и Mixcolumn и обратные к ним преобразования для всех элементов поля (в виде таблицы). Все шаги алгоритма оформить в виде двух состояний – вход-выход.
Задание 2.
В таблице 2 приведены открытые ключи собеседника по секретной переписке с помощью алгоритма RSA и его секретное зашифрованное сообщение. Требуется:
1. Выработать свои секретные ключи.
2. Расшифровать посланное секретное сообщение.
3. Выработать общий ключ для обеспечения секретности на основе открытого ключа.
4. Послать абоненту расшифрованное верифицированное сообщение (т.е. сообщение и его цифровая подпись)
Задание 3.
Открытый элемент Р задан в табл. 3 – графа 2. Найти примитивный элемент поля. Считая, что секретный ключ каждого участника равен номеру студента в списке группы i , вычислить ключ обмена для участника с номером 35 – i по алгоритму Диффи – Хэллмана
Задание 4
Зашифровать поговорку, выбранную из списка в соответствии с номером студента в группе различными спопобами:
1. спомощью способов, указанных в таблице3. графа 2;
2. С помощью ключа (пароля), где в качестве ключа используем:
1. константу с=3;
2. следующую в списке поговорку, используя алфавит Z33 = (А….Я, е=ё + пробел);
3. псевдослучайную последовательность, сгенерированную линейным рекуррентным генератором. Зашифровать 7 первых символов, используя алфавит Z32 и равномерный код. ПСП генерируется матрицей 5*5.
Полученное сообщение подписать, используя алгоритм Эль - Гамаля. В качестве хэш-функции использовать сумму пятиразрядных блоков по модулю 2
Примеры выполнения задания
Пример выполнения Задания1. Упрощенный алгоритм Rijndael,.
Построение поля
Вариант № 7, группа 2091 (№ 1)
Номер в списке группы i = 7
Номер группы k = 1
В приведенных арифметических выражениях вся арифметика в GF(24).
За неприводимый многочлен возьмем P(x) = x4+x+1.
Тогда за примитивный элемент можно взять a = x.
Элементы поля
| a | 0010 | 2 | x | a6 | 1100 | 12 | x3+x2 | a11 | 1110 | x3+x2+x | 14 |
| a2 | 0100 | 4 | x2 | a7 | 1011 | 11 | x3+x+1 | a12 | 1111 | x3+x2+x+1 | 15 |
| a3 | 1000 | 8 | x3 | a8 | 0101 | 5 | x2+1 | a13 | 1101 | x3+x2+1 | 13 |
| a4 | 0011 | 3 | x+1 | a9 | 1010 | 10 | x3+x | a14 | 1001 | x3+1 | 9 |
| a5 | 0110 | 6 | x2+x | a10 | 0111 | 7 | x2+x+1 | a15 | 0001 | 1 | 1 |
Обратные элементы
| a-1 | a14 | a-6 | a9 | a-11 | a4 |
| a-2 | a13 | a-7 | a8 | a-12 | a3 |
| a-3--3 | a12 | a-8 | a7 | a-13 | a2 |
| a-434 | a11 | a-9 | a6 | a-14 | a |
| a35-5 | a10 | a-10 | a5 | a-15 | a15 |
Многочлены для ByteSub
| № | P(x) | P1(x) | C(x) |
| 7 | 7 | 6 | 1, 13 |
p(x) = 710 = 01112 = x2 + x + 1 = a10
p1(x) = 610 = 01102 = x2 + x = a5
Многочлен для MixColumn
c(x) = x + 13 = 0001 * x + 1101
Ключ К
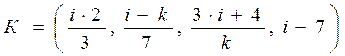
i * 2 / 3 = 7 * 2 / 3 = a10 * a * a-4 = a11 * a11 = a15 * a7 = a7 = 10112
(i – k) / 7 = (7 - 1) / 7 = (0111 + 0001) * a-10 = 0110 * a5 = a5 * a5 = a10 = 01112
(3 * i + 4) / k = (3 * 7 + 4) / 1 = (a4 * a10 + 0010) = a14 + 0010 = 1001 + 0010 = 10112
i – 7 = 7 – 7 = 0
K = (1011 0111 1011 0000)
Открытый текст P
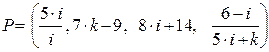
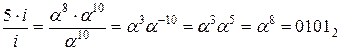
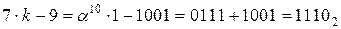
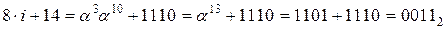
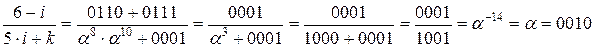
P = (0101 1110 0011 0010)
S преобразование и обратное для всех элементов
p(x) = 710 = 01112 = x2 + x + 1 = a10
p1(x) = 610 = 01102 = x2 + x = a5
S(x) = x-1 p + p1
S(0) = a5 = 0110
S(a) = a-1 a10 + a5 = a14 a10 + 0110 = a9 + 0110 = 1010 + 0110 = 1100
S(a2) = a-2 a10 + a5 = a13 a10 + 0110 = a8 + 0110 = 0101 + 0110 = 0011
S(a3) = a-3 a10 + a5 = a12 a10 + 0110 = a7 + 0110 = 1011 + 0110 = 1101
S(a4) = a-4 a10 + a5 = a11 a10 + 0110 = a6 + 0110 = 1100 + 0110 = 1010
S(a5) = a-5 a10 + a5 = a10 a10 + 0110 = a5 + 0110 = 0110 + 0110 = 0000
S(a6) = a-6 a10 + a5 = a9 a10 + 0110 = a4 + 0110 = 0011 + 0110 = 0101
S(a7) = a-7 a10 + a5 = a8 a10 + 0110 = a3 + 0110 = 1000 + 0110 = 1110
S(a8) = a-8 a10 + a5 = a7 a10 + 0110 = a2 + 0110 = 0100 + 0110 = 0010
S(a9) = a-9 a10 + a5 = a6 a10 + 0110 = a1 + 0110 = 0010 + 0110 = 0100
S(a10) = a-10 a10 + a5 = a5 a10 + 0110 = 0001 + 0110 = 0111
S(a11) = a-11 a10 + a5 = a4 a10 + 0110 = a14 + 0110 = 1001 + 0110 = 1111
S(a12) = a-12 a10 + a5 = a3 a10 + 0110 = a13 + 0110 = 1101 + 0110 = 1011
S(a13) = a-13 a10 + a5 = a2 a10 + 0110 = a12 + 0110 = 1111 + 0110 = 1001
S(a14) = a-14 a10 + a5 = a1 a10 + 0110 = a11 + 0110 = 1110 + 0110 = 1000
S(a15) = a-15 a10 + a5 = a15 a10 + 0110 = a10 + 0110 = 0111 + 0110 = 0001
Обратные преобразования
| S-1(0110) = 0 = 0000 S-1(1100) = a = 0010 S-1(0011) = a2 = 0100 S-1(1101) = a3 = 1000 S-1(1010) = a4 = 0011 S-1(0000) = a5 = 0110 S-1(0101) = a6 = 1100 S-1(1110) = a7 = 1011 | S-1(0010) = a8 = 0101 S-1(0100) = a9 = 1010 S-1(0111) = a10 = 0111 S-1(1111) = a11 = 1110 S-1(1011) = a12 = 1111 S-1(1001) = a13 = 1101 S-1(1000) = a14 = 1001 S-1(0001) = a15 = 0001 |
Расширение ключа, цикловые константы
C[2] = RC[2] 0000 = a1 0000 = 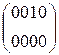
C[4] = RC[4] 0000 = a3 0000 = 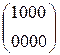
C[6] = RC[6] 0000 = a5 0000 = 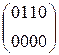
W[0] = Key[0] = 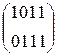
W[1] = Key[1] = 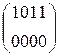
W[2] = W[0] + SB(R(W[1])) + C[2] = 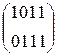 + SB(R(
+ SB(R( 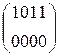 )) +
)) + 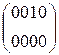
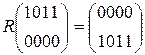
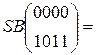
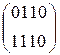
W[2] = 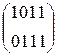 +
+ 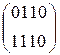 +
+ 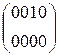 =
= 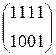
W[3] = W[1] + W[2] = 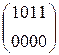 +
+ 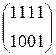 =
= 
W[4] = W[2] + SB(R(W[3])) + C[4] = 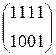 + SB(R(
+ SB(R(  )) +
)) + 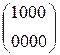
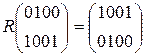
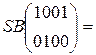
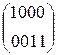
W[4] = 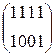 +
+ 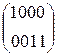 +
+ 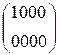 =
= 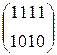
W[5] = W[3] + W[4] =  +
+ 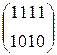 =
= 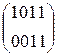
W[6] = W[4] + SB(R(W[5])) + C[6] = 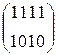 + SB(R(
+ SB(R( 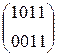 )) +
)) + 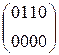
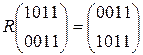
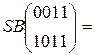
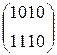
W[6] = 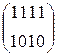 +
+ 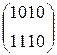 +
+ 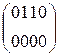 =
= 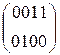
Шифрование
0) 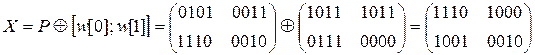
1.1) SubBytes
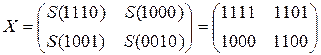
1.2) ShiftRow
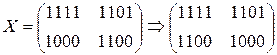
1.3) MixColumn
c(x) = x + 13 = 0001 * x + 1101
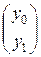 =
= 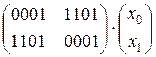
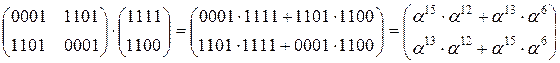 =
=
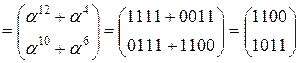
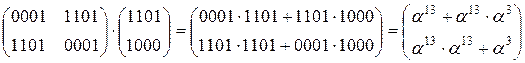 =
=
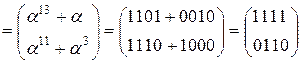
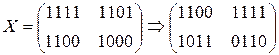
1.4) AddRoundKey
W[2] = 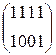 W[3] =
W[3] = 
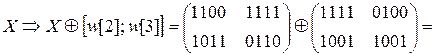
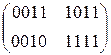
2.1) SubBytes
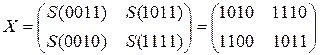
2.2) ShiftRow
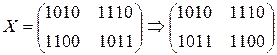
2.3) AddRoundKey
W[4] = 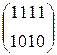 W[5] =
W[5] = 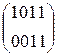
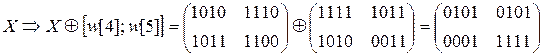
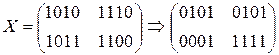
Зашифрованный текст
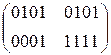 С = (5, 1, 5, 15)
С = (5, 1, 5, 15)
Расшифровка
0) x = x + k2
1.1) x = r -> (x)
1.2) x = s-1 (x)
1.3) x = x + k1
1.4) x = m-1 x
2.1) x = r -> (x)
2.2) x = s-1 (x)
2.3) x = x + k0
0) 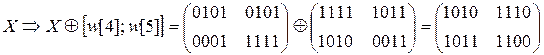
1.1) ShiftRow >
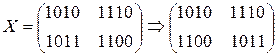
SubBytes
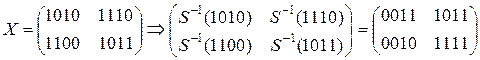
AddRoundKey
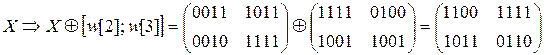
1.4) MixColumn
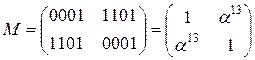
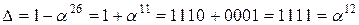
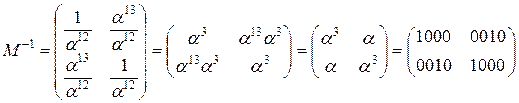
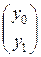 =
= 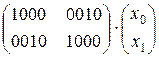
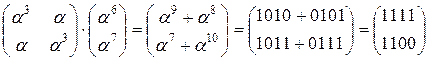
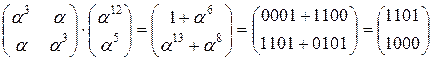
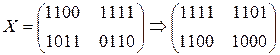
2.1) ShiftRow >
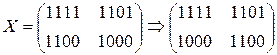
2.2) SubBytes
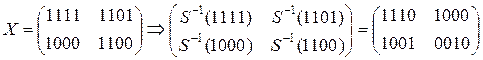
2.3) AddRoundKey
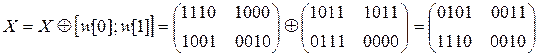
P = (0101 1110 0011 0010)
После шифровки и расшифровки был получен исходный открытый текст.
Пример выполнения Задания1. Упрощенный алгоритм Rijndael,.
ПОСТРОЕНИЕ ПОЛЯ
В приведенных арифметических выражениях вся арифметика в GF(24).
Неприводимый многочлен P(x) = x4+x+1.
Примитивный элемент a = x.
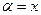
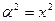
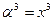
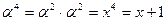
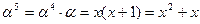
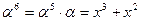
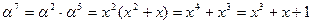
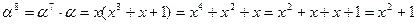
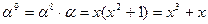
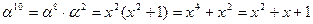
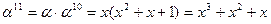
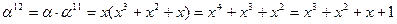
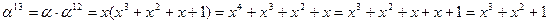
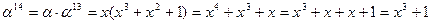
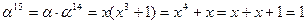
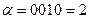
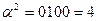
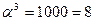
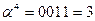
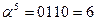
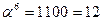
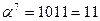
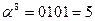
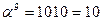
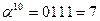
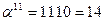
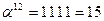
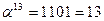
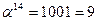
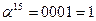
Обратные элементы:
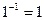
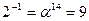
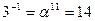
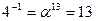
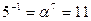
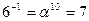
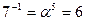
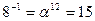
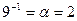
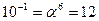
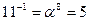
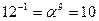
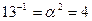
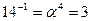
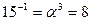
ПАРАМЕТРЫ АЛГОРИТМА
i = 15, k = 1
Многочлены для ByteSub :
p1(x) = 12 = 1100 = x3 + x2
p0(x) = 4 = 0100 = x2
Многочлен для MixColumn :
с(x) = 6x + 11 = 0110*x + 1011
Открытый ключ К:
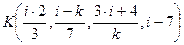
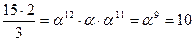
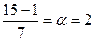
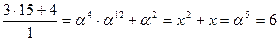
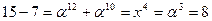
K = (10, 2, 6, 8)
| 1010 | 0110 |
| 0010 | 1000 |
Открытый текст:
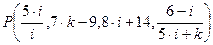
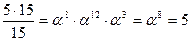
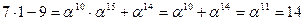
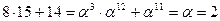
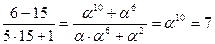
P = (5, 14, 2, 7)
| 0101 | 0010 |
| 1110 | 0111 |
S - box и обратное преобразование:
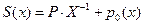
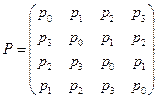 =
= 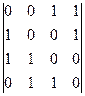
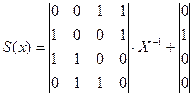

Обратное преобразование:
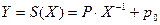 ;
;
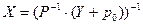 ;
;
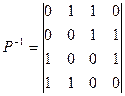 ; S -1:
; S -1: 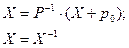
7
Матрица М:
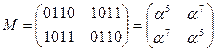
Матрица 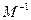 :
:
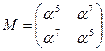
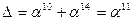
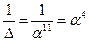
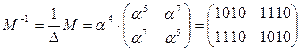
| x | x-1 | S(x) | S-1(x) | ||
| 0 | 0000 | 0 | 0000 | 0100 | 0010 |
| α | 0010 | 2 | 1001 | 1110 | 1111 |
| α2 | 0100 | 4 | 1101 | 1101 | 1001 |
| α3 | 1000 | 8 | 1111 | 0100 | 0011 |
| α4 | 0011 | 3 | 1110 | 1000 | 0001 |
| α5 | 0110 | 6 | 0111 | 0010 | 1111 |
| α6 | 1100 | 12 | 1010 | 1011 | 1110 |
| α7 | 1011 | 11 | 0101 | 1011 | 1100 |
| α8 | 0101 | 5 | 1011 | 0111 | 1110 |
| α9 | 1010 | 10 | 1100 | 0001 | 0111 |
| α10 | 0111 | 7 | 0110 | 1110 | 0101 |
| α11 | 1110 | 14 | 0011 | 0101 | 0010 |
| α12 | 1111 | 15 | 1000 | 0010 | 0010 |
| α13 | 1101 | 13 | 0100 | 0111 | 0100 |
| α14 | 1001 | 9 | 0010 | 1101 | 1010 |
| α15 | 0001 | 1 | 0001 | 1000 | 1010 |
Дата: 2019-03-05, просмотров: 442.