Предложенный К. Ремишем метод во многих источниках называют универсальным, поскольку он позволяет определять просадку у судов как носом, так и кормой с учетом их геометрических обводов:

,

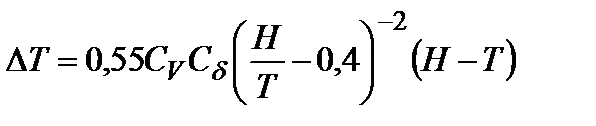(4.6)

где 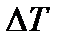  – приращение осадки носом или кормой, м;

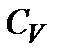 – коэффициент, зависящий от скорости хода;

 – коэффициент, зависящий от формы корпуса.

Коэффициент 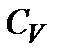 рассчитывается по выражению

,

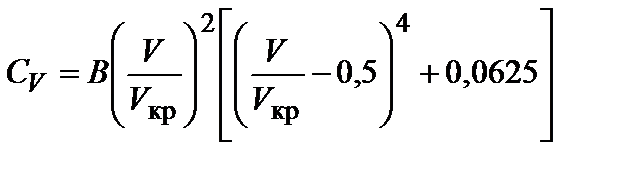(4.7)

где 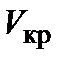 – критическая скорость для мелководья, определяемая по формуле

.

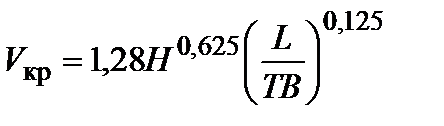(4.8)

Коэффициент  отдельно для носовой части и для кормы определяется по выражениям:

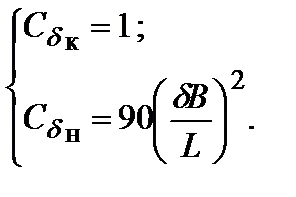
(4.9)

Как видно из формулы (4.7), при 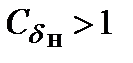 проседание носа больше, чем проседание кормы, а при  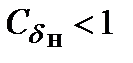– больше проседание кормы. Также можно сделать вывод, что у судов с полными обводами и малым отношением  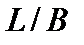(например, у крупнотоннажных танкеров или балкеров) больше проседает нос, в то время как у судов с острыми образованиями корпуса больше проседает корма.

Однако данный метод не может быть применен к речным судам, поскольку у них приращение осадки по корме всегда больше, хотя величина 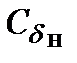 может быть как больше, так и меньше 1.

В.П. Смирновым предложено расчетное выражение, которое позволяет также учитывать начальный дифферент морского судна:

.

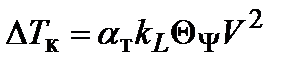(4.10)

здесь 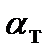 – коэффициент пропорциональности (табл. 4.2);

Таблица 4.2

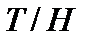
	0,35	0,4	0,5	0,6	0,7	0,75	0,8	0,85
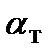
	0,0146	0,0156	0,0174	0,0201	0,0232	0,0250	0,0274	0,0296

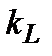 – коэффициент пропорциональности, учитывающий длину судна. Его значения приведены в табл. 4.3;

Таблица 4.3

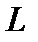
	до 100 м	100 – 150 м	Более 150 м
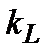
	095	1,05	1,25

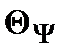 – коэффициент пропорциональности, учитывающий начальный дифферент на корму. Его значения приведены в табл. 4.4.

Таблица 4.4

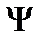
	0	1,0
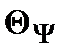
	1,0	1,025	1,05

В.Г. Павленко предложил метод для определения приращения динамической просадки речных судов и толкаемых составов по корме:

,

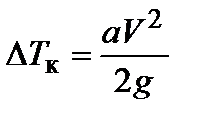(4.11)

где 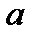 – числовой коэффициент:

для речных самоходных судов водоизмещением менее 2000 т

;

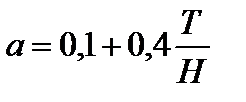(4.12)

 для грузовых судов и составов водоизмещением более 2000 т

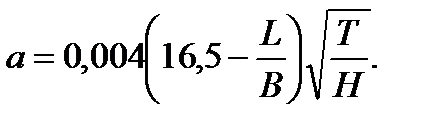
(4.13)

А.М. Полунин уточнил расчетные зависимости для судов средних размеров, эксплуатируемых в бассейнах сибирских рек:

для грузовых теплоходов

;

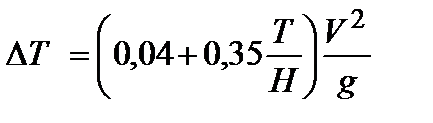(4.14)

для пассажирских судов

.

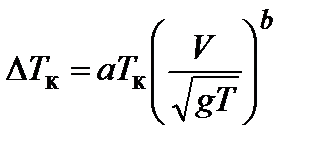(4.15)

Здесь 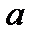 и 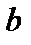 – числовые коэффициенты, определяемые по выражениям:

;

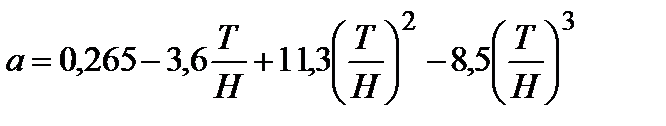(4.16)

.

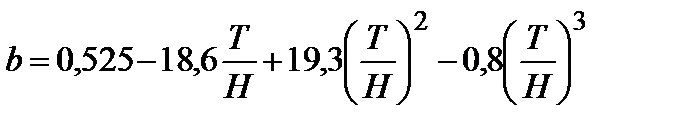(4.17)

Данные расчетные зависимости справедливы для .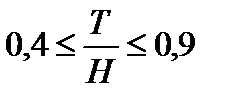

Анализ приведенных методов, выполненный М.Ю. Чуриным, позволил выявить у них общий недостаток. Они не учитывают форму судовых обводов, которые несомненно оказывают влияние на величину динамической просадки. Чурин предложил расчетные формулы, устраняющие указанный недостаток:

,

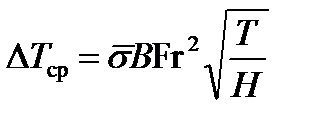(4.18)

где 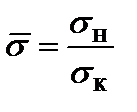 – отношение коэффициента полноты носовой и кормовой половин диаметрального батокса корпуса судна;

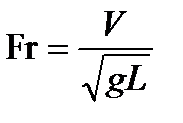 – число Фруда.

Выражение (4.16) позволяет определить приращение средней осадки судна. При расчете просадки по корме результат расчета следует увеличить на 20%.

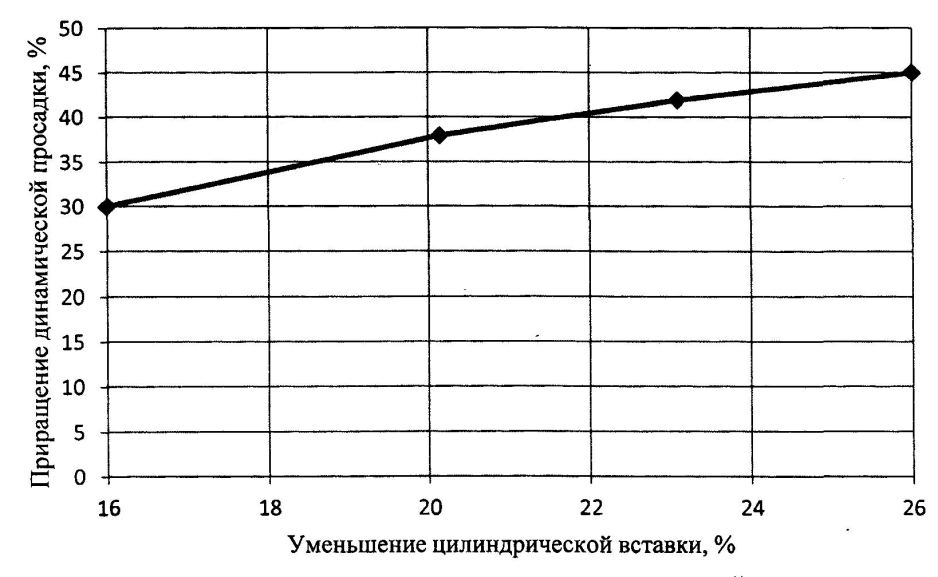
Дополнительно им исследован вопрос изменения просадки судов смешанного (река-море) плавания, прошедших реконструкцию в виде уменьшения длины цилиндрической вставки и укрепления корпуса для улучшения их мореходных качеств. В итоге установлено, что у данных судов приращение осадки по корме на мелководье больше на 30–45% по сравнению с судами базового проекта (рис. 4.6).

Рис. 4.6. График зависимости приращения динамической просадки по корме реконструированных судов при уменьшении длины, выраженной в процентах от первоначальной длины судна

Приведенная графическая зависимость хорошо аппроксимируется полиномной зависимостью:

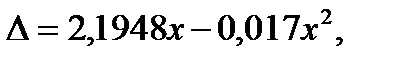
(4.19)

где  – приращение просадки по корме, выраженной в процентах от просадки по корме судна базового проекта до реконструкции;

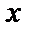 – уменьшение длины судна, выраженное в процентах от первоначальной длины.