1. Включить прибор, нажатием клавиши .

2. Произвести подготовку к измерениям по указанному выше последовательному алгоритму.

3. Расположить газозаборный зонд в необходимом месте для производства измерений.

4. Считать с цифрового индикатора измеренное значение О_{2 возд} или СО_-нер необходимое количество раз. Данные необходимо занести в табл. 28.

6. После окончания измерений выключить прибор, нажатием на клавишу .

7. Провести обработку полученных экспериментальных данных по методике, описанной ниже в разделе «Обработка результатов прямых многократных измерений».

9. Составить отчет по работе.

Таблица 28

Результаты измерений

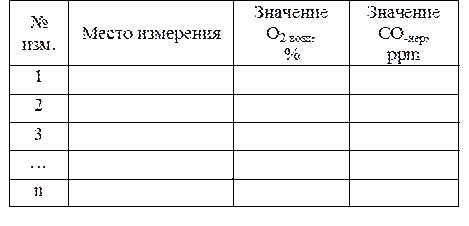
Обработка результатов прямых многократных измерений

Последовательность обработки результатов прямых многократных измерений состоит из ряда этапов.

Определение точечных оценок закона распределения

Результатов измерений

На этом этапе определяется среднее арифметическое значение 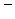 измеряемой величины, СКО результата измерений S_x .

В соответствии с критериями, исключаются грубые погрешности, после чего проводится повторный расчет оценок среднего арифметического значения и его СКО.

5.2.Определение закона распределения результатов

Измерений или случайных погрешностей

Здесь по результатам измерений и проведенным расчетам строится гистограмма или полигон распределения результатов наблюдений. По виду построенных зависимостей оценивается закон распределения результатов измерений.

Оценка закона распределени по статистическим критериям

При числе измерений n >50 для идентификации закона распределения используем критерий Пирсона. При 50>n>15 для проверки нормальности закона распределения применяем составной критерий. При n<15 принадлежность экспериментального распределения к нормальному не проверяется.

Определение доверительных границ случайной погрешности

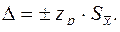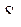Если удалось идентифицировать закон распределения результатов измерений, то с его использованием находится квантильный множитель z_p при заданном значении доверительной вероятности Р. В этом случае доверительные границы случайной погрешности  Здесь  – СКО среднего арифметического значения. При n<30 часто используют распределение Стьюдента, при этом доверительные границы случайной погрешности

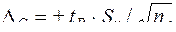                          (41)

где t_P – коэффициент Стьюдента, приведенный в табл. 29, n – количество измерений.