Для дальнейшего расчета энтропии ЭЭГ сигнала используется программа Entropy 3.0.
В данной программе осуществляется предварительное локально-ранговое кодирование (ЛРК), которое необходимо для того, чтобы исключить ошибки, связанные с масштабированием ЭЭГ сигнала и обратимыми изменениями его амплитуды, а также вычисление SE с записью
27
|
|
| A={a,b,c,d,…,z}. |
результатов вычисления в текстовый файл в виде последовательности отсчетов.
Окно программы Entropy 3.0 представлен на рисунке 2.7.
Рисунок 2.7 – Окно программы Entropy 3.0
Рассмотрим подробнее алгоритм ЛРК исходного ряда с помощью
выбранного алфавита.
Имеется последовательность x(i),i=1…N , каждому элементу которой
ставится в соответствие символ выбранного алфавита
Алфавит А однозначно определяет соотношение £ между своими символами и формирует однозначное отображение – ранговое ядро R .
Для данного случая алгоритм ЛРК будет выглядеть следующим образом:
1) выбор размера окна W , в рамках которого будет производиться
анализ;
2) формирование сигнатуры S i , в которой содержится информация о
соотношениях текущего элемента с соседними, в рамках заданного окна. При этом:
28
|
|
| S j =i |
| ì | 1, x(i)ñx(i + j + | W | ) | |||||||||||
| ï | ||||||||||||||
| 2 | , | (2.4) | ||||||||||||
| S = í | ||||||||||||||
| ï0, x(i) ³ x(i + j + | W | ) | ||||||||||||
|
| ||||||||||||||
| î | 2 | |||||||||||||
| где | j = 0...W , j ¹ | W | , i = 1...N - | W | ; | |||||||||
| 2 | 2 | |||||||||||||
3) выбор сигнатуры S i , которая для всех j имеет значение ноль;
4) запись текущего символа алфавита в соответствующую ячейку рангового ядра R(i) (первому проходу соответствует минимум значения
функции на исследуемом интервале);
5) обнуление результатов сравнения всех элементов с текущим x(i)
путем присвоения все сигнатурам значения ноль;
6) задание следующего символа алфавита A = {a, b, c, d,...z};
7) проверка всех ячеек рангового ядра R на заполнение;
8) окончание процедуры формирования рангового ядра R происходит после заполнения всех ячеек, в противном случае повторяется процедура с выбора новой сигнатуры S i .
Построение графика изменения энтропии для разработанной модели ЭЭГ сигнала при эпилепсии производится в программе Microsoft Excel (рисунок 2.8).
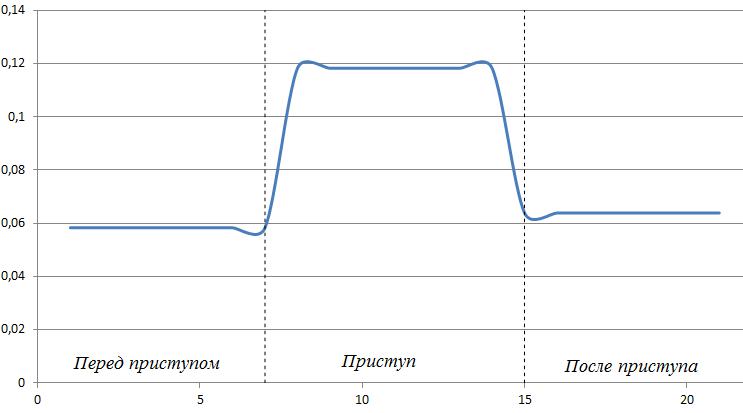
Рисунок 2.8 – Энтропия модели ЭЭГ сигнала
29
Выводы по главе 2
1. Произведено математическое моделирование ЭЭГ сигнала при эпилепсии.
2. Произведен расчет спектральных характеристик для разработанной модели ЭЭГ сигнала при эпилепсии.
3. Проведена апробация предложенной методики на разработанной модели ЭЭГ сигнала при эпилепсии.
4. В результате исследования, проведенного на разработанной математической модели ЭЭГ сигнала при эпилепсии, можно сделать вывод,
что предложенная методика имеет высокую ценность в диагностике эпилепсии по энтропии ЭЭГ сигнала.
30
ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ПРЕДЛАГАЕМОЙ МЕТОДИКИ
Описание материалов
Реальные ЭЭГ сигналы были получены из базы PhysioNet [5]. База данных, собранная в детской больнице Бостона, состоит из записей ЭЭГ пациентов с эпилепсией. К каждой записи прилагается файл «subject_info», который содержит информацию о возрасте и половой принадлежности пациента. Каждый случай содержит от 9 до 42 непрерывных файлов от одного пациента в формате edf. В большинстве случаев edf-файлы содержат ровно один час оцифрованных ЭЭГ сигналов. Все сигналы записаны при частоте дискретизации 256 Гц с разрешением 16 бит. Большинство ЭЭГ сигналов записаны в 23 отведениях (FP1–F7, F7–T7, T7–P7, P7–O1, FP1–F3, F3–C3, C3–P3, P3–O1, FP2–F4, F4–C4, C4–P4, P4–O2, FP2–F8, F8–T8, T8–P8, P8–O2, FZ–CZ, CZ–PZ, P7–T7, T7–FT9, FT9–FT10, FT10–T8, T8–P8). Для записи ЭЭГ сигналов использовалась международная система позиций электродов 10–20.
Для исследования было отобрано 5 ЭЭГ сигналов, краткое описание которых представлено в таблице 3.1.
Таблица 3.1 – Краткое описание выбранных ЭЭГ сигналов
| Параметр | Испытуемый | |||||
| 1 | 2 | 3 | 4 | 5 | ||
| Начало | 01:44:44 | 02:44:51 | 04:45:06 | 12:34:22 | 02:51:30 | |
| записи | ||||||
| Окончание | 02:44:44 | 03:44:51 | 05:45:06 | 13:13:07 | 03:51:30 | |
| записи | ||||||
| Количество | 1 | 1 | 1 | 1 | 1 | |
| приступов | ||||||
31
Продолжение таблицы 3.1.
| Параметр | Испытуемый | |||||
| 1 | 2 | 3 | 4 | 5 | ||
| Время | ||||||
| начала | 1732 | 1015 | 1720 | 1862 | 2592 | |
| приступа, с | ||||||
| Время | ||||||
| окончания | 1772 | 1066 | 1810 | 1963 | 2656 | |
| приступа, с | ||||||
Дата: 2019-03-05, просмотров: 366.