Необходимые сведения
· Для вычисления интеграла от функции 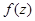 по кривой
по кривой 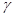 необходимо
необходимо
выбрать параметризацию кривой 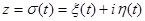 ,
, 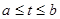 , после чего криволинейный интеграл сводится к определённому интегралу в соответствии с формулой:
, после чего криволинейный интеграл сводится к определённому интегралу в соответствии с формулой:
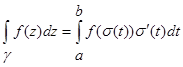
· Интегральная формула Коши для функции:
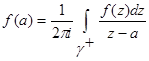
· Интегральная формула Коши для производной:
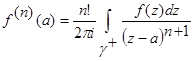
· При интегрировании многозначной функции необходимо выделять её однозначную ветвь.
Задачи для решения в аудитории
1.Вычислить интеграл от функции 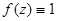 по кривой
по кривой 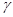 .
.
2.Вычислить интеграл от функции 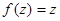 по кривой
по кривой 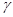 .
.
3.Вычислить интеграл от функции 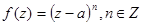
по окружности 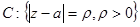 , ориентированной положительно.
, ориентированной положительно.
4.Вычислить интеграл от функции 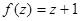 по следующим кривым:
по следующим кривым:
а) 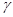 :
: 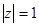 б)
б) 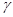 :
: 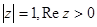 в)
в) 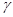 :
: 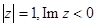
г) 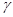 : отрезок, соединяющий начало координат с точкой
: отрезок, соединяющий начало координат с точкой 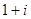
5.Вычислить интеграл по кривой 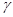 :
: 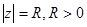 от следующих функций:
от следующих функций:
а) 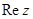 б)
б) 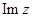 в)
в) 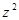 г)
г) 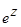
6.С помощью интегральной формулы Коши вычислить интегралы (все окружности обходятся против часовой стрелки):
а) 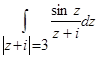 б)
б) 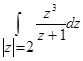 в)
в) 
г) 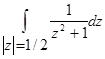 д)
д) 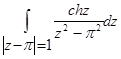 г)
г) 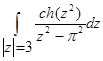
Какой другой способ решения Задания 6 можно предложить?
7.С помощью интегральной формулы Коши для производной вычислить интегралы (все окружности обходятся против часовой стрелки):
а) 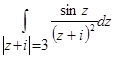 б)
б) 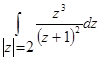 в)
в) 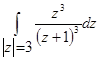
г) 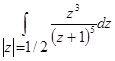 д)
д) 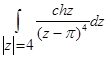 е)
е) 
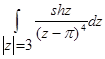
Какой другой способ решения Задания 7 можно предложить?
8.Вычислить интегралы по заданным контурам (обратить внимание на многозначность подынтегральной функции):
а) 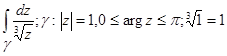 б)
б) 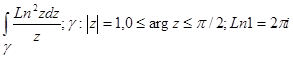
в) 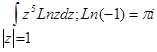
Домашнее задание
1.Ефимов-Поспелов, том 3, №№ 13.230-13.242, 13.243, 13.245, 13.247, 13.248, 13.249-13.256, двумя способами №№13.257-13.271
Занятие 5
Комплексные ряды
Необходимые сведения
1. Функция, регулярная в круге 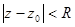 , раскладывается в ряд Тейлора:
, раскладывается в ряд Тейлора:
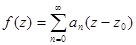
2. Функция, регулярная в кольце 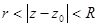 , раскладывается в ряд Лорана:
, раскладывается в ряд Лорана:
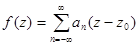 =
= 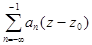 +
+ 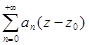
3. Для разложения функций в степенные ряды необходимо повторить разложение основных элементарных функций и формулу суммы бесконечно убывающей геометрической прогрессии (см. занятие 7 за 3 семестр)
Задания для решения в аудитории
1.Разложить функции в ряд по степеням z всеми возможными способами , указать области сходимости полученных рядов, изобразить их на плоскости С:
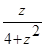 ;
; 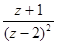 ;
; 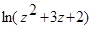 ;
; 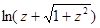
2.Разложить функции в ряд по степеням 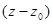 , определить области сходимости полученных рядов, изобразить их на плоскости С:
, определить области сходимости полученных рядов, изобразить их на плоскости С:
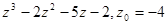 ;
; 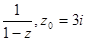 ;
; 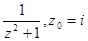 ;
; 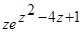 ,
, 
3.Найти области сходимости рядов, изобразить их на плоскости С:
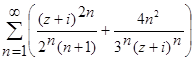 ,
, 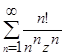
4.Найти все разложения функций в ряды Лорана по степеням 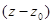 , установить области сходимости полученных разложений, сделать рисунок:
, установить области сходимости полученных разложений, сделать рисунок:
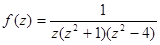 ,
, 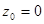 ;
; 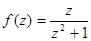 ,
, 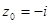
5.Найти разложение функции в ряд по степеням 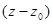 в указанной области:
в указанной области:
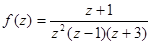 ;
; 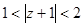
Домашнее задание
Ефимов-Поспелов, том 3:
№№13.226 – 13.229,
12.179, 12.181, 12.187 - 12.189.
12.217, 12.221, 12.226, 12.236, 12.241, 12.348, 12.350, 12.351.
12.352 – 12.375 (полезно сделать все, обязательно: любые 10 штук)
Занятие 6
Изолированные особые точки
Необходимые сведения
1. Точка 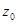 называется нулём функции
называется нулём функции 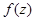 кратности
кратности 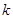 , если
, если 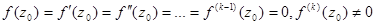
2. Точка 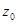 является нулём функции
является нулём функции 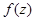 кратности
кратности 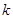
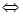 функция
функция
представима в виде 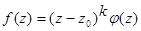 , где
, где 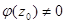
3. Точка, в которой функция не регулярна, называется особой точкой.
4. Если существует такая окрестность особой точки, в которой нет других особых точек, то эта особенность называется изолированной.
5. Изолированные особые точки можно разделить на три типа (см. таблицу)
Таблица: «Классификация особых точек»
| № |
Тип особой точки 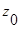
| Определение с помощью предела | Определение с помощью главной части ряда Лорана |
| 1 | Устранимая особая точка |
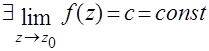
| Главная часть ряда Лорана отсутствует |
| 2 |
Полюс порядка 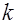
|
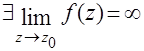
|
В главной части ряда Лорана конечное число слагаемых, максимальная отрицательная степень = 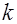
|
| 3 | Существенная особенность |
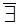 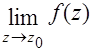 ни конечного, ни бесконечного
ни конечного, ни бесконечного
| В главной части ряда Лорана бесконечное число слагаемых |
6. Полюс первого порядка по-другому называют простым полюсом.
7. Связь между нулями и полюсами: если точка 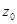 является нулём функции
является нулём функции 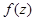 кратности
кратности 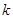 , то эта точка является полюсом порядка
, то эта точка является полюсом порядка 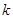 для функции
для функции 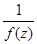
Задания для решения в аудитории
1. Определить все нули и их порядок для функций:
(а) 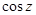 (б)
(б) 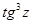 (в)
(в) 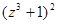 (г)
(г) 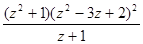
2. Найти все конечные особые точки, указать их характер, в случае полюса – его порядок , для функций:
(а) 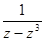 (б)
(б) 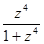 (в)
(в) 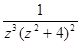 (г)
(г) 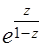 (д)
(д) 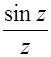 (е)
(е) 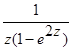
3. Определить характер особенности в точке 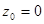 , разложив функцию
, разложив функцию 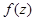 в ряд Лорана в окрестности этой точки и выделив главную часть полученного ряда:
в ряд Лорана в окрестности этой точки и выделив главную часть полученного ряда:
(а) 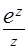 ;
; 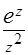 ;
; 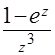 ;
; 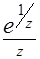 ;
; 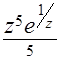 ;
; 
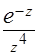
(б) 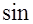 (
( 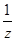 );
); 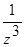
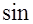 (
( 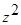 );
); 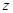
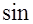
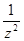 ;
; 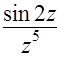 ;
; 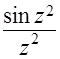
(в) 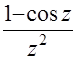 ;
; 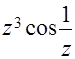 ;
; 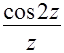 ;
; 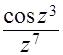 ;
; 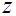
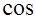
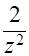
4. Исследовать поведение функции на бесконечности:
(а) 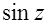 (б)
(б) 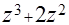 (в)
(в) 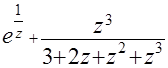
Домашнее задание
Определить все нули и их порядок для функций:
(а) 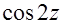 (б)
(б) 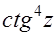 (в)
(в) 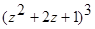 (г)
(г) 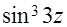
Ефимов-Поспелов, том 3: № № 12.382 – 12.407
Занятие 7
Вычеты
Применение вычетов
Необходимые сведения
1. Определение вычета: 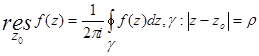
2. Отыскание вычета по ряду Лорана: 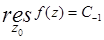 – коэффициент ряда Лорана в окрестности особой точки
– коэффициент ряда Лорана в окрестности особой точки 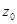
3. Вычисление вычета в простом полюсе:
(а) 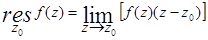
(б) Если 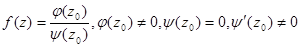 , тогда
, тогда 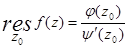
4. Вычисление вычета в кратном полюсе:
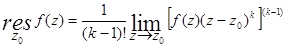
5. Основная теорема о вычетах: Если функция 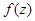 регулярна в ограниченной замкнутой области D за исключением конечного числа изолированных особых точек
регулярна в ограниченной замкнутой области D за исключением конечного числа изолированных особых точек 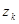 (k=1,…n), то интеграл по границе
(k=1,…n), то интеграл по границе 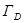 этой области вычисляется по формуле:
этой области вычисляется по формуле: 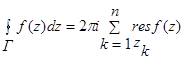
6. Вторая теорема о вычетах: сумма вычетов по всем особым точкам, считая бесконечно удалённую, равна нулю.
7. Алгоритм вычисления интеграла по замкнутому контуру с помощью вычетов:
· Контур интегрирования изобразить на плоскости
· Найти все особые точки подынтегральной функции (изобразить на плоскости)
· Отметить те точки , которые попадают внутрь контура интегрирования
· Определить их тип и найти вычеты в этих точках
· Просуммировать полученные вычеты и воспользоваться основной теоремой о вычетах
Задачи для решения в аудитории
1.Найти вычеты функций в особых конечных точках:
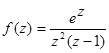 ;
; 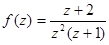 ;
; 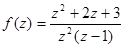 ;
;
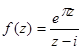 ;
; 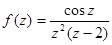 ;
; 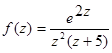 ;
;
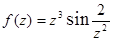 :
: 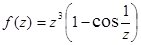 ;
; 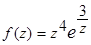 ;
; 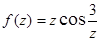
2.Определить характер бесконечно удалённой точки и найти вычет:
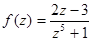 ;
; 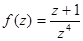 ;
; 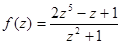 ;
;
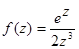 ;
; 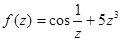 ;
; 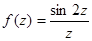 ;
;
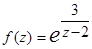 ;
; 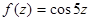 ;
; 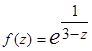 ;
;
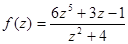 ;
; 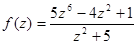 ;
; 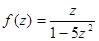 ;
;
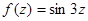 ;
; 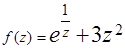 ;
; 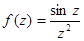 ;
; 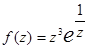 .
.
3.Вычислить интеграл:
a) 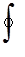
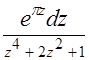 б)
б) 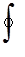
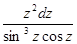 в)
в) 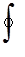
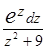
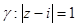
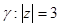
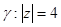
г) 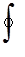
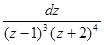 д)
д) 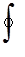
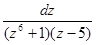 е)
е) 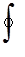
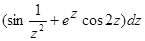
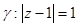
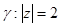
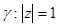
Домашнее задание
1. Ефимов, Поспелов, т.3, №№ 12.408 – 12.449
Занятие 8
Дата: 2019-03-05, просмотров: 327.