Занятие № 1
Комплексные числа.
Необходимые сведения.
I. Комплексным числом 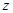 называется пара действительных чисел
называется пара действительных чисел 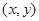 . Для комплексных чисел определено понятие равенства, сложения, умножения. Комплексные числа не сравниваются! Два комплексных числа
. Для комплексных чисел определено понятие равенства, сложения, умножения. Комплексные числа не сравниваются! Два комплексных числа 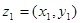 и
и 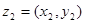 равны тогда и только тогда, когда
равны тогда и только тогда, когда 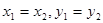 . Суммой двух комплексных чисел называется комплексное число
. Суммой двух комплексных чисел называется комплексное число 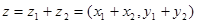 . Произведением двух комплексных чисел называется комплексное число
. Произведением двух комплексных чисел называется комплексное число 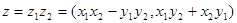 . Комплексное число (0,1) называется мнимой единицей и обозначается символом
. Комплексное число (0,1) называется мнимой единицей и обозначается символом 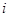 . Это число обладает свойством
. Это число обладает свойством 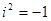 . Обычно комплексное число записывают в форме z= x+ iy. Эта запись называется алгебраической формой комплексного числа, причём
. Обычно комплексное число записывают в форме z= x+ iy. Эта запись называется алгебраической формой комплексного числа, причём 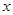 называется действительной частью и обозначается символом
называется действительной частью и обозначается символом 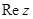 , а
, а 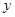 называется мнимой частью и обозначается символом
называется мнимой частью и обозначается символом 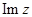 . Комплексное число
. Комплексное число 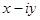 называется сопряжённым комплексному числу
называется сопряжённым комплексному числу 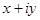 и обозначается символом
и обозначается символом 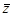 .Действительное положительное число
.Действительное положительное число 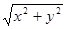 называется модулем комплексного числа и обозначается символом
называется модулем комплексного числа и обозначается символом 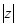 .
.
II. Комплексные числа можно изображать на плоскости.Каждое число z= x+ iy отождествляется с точкой плоскости с координатами 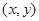 . Действительные числа отмечаются на оси абсцисс, поэтому её называют действительной осью, а чисто мнимые числа отмечаются на оси ординат, поэтому её называют мнимой осью. Комплексное число
. Действительные числа отмечаются на оси абсцисс, поэтому её называют действительной осью, а чисто мнимые числа отмечаются на оси ординат, поэтому её называют мнимой осью. Комплексное число 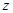
 изображается также вектором с началом в точке 0 и концом в точке
изображается также вектором с началом в точке 0 и концом в точке 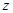 . Модуль комплексного числа имеет смысл длины этого вектора. Угол наклона вектора к положительному направлению действительной оси называется главным значением аргумента, он обозначается символом
. Модуль комплексного числа имеет смысл длины этого вектора. Угол наклона вектора к положительному направлению действительной оси называется главным значением аргумента, он обозначается символом 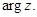
III. Любое комплексное число можно записать в виде 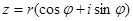 , где
, где 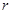 - модуль, а
- модуль, а 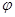 – аргумент комплексного числа. Такая форма называется тригонометрической формой записи комплексного числа. Комплексные числа
– аргумент комплексного числа. Такая форма называется тригонометрической формой записи комплексного числа. Комплексные числа 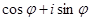 и
и 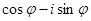 можно обозначить символами
можно обозначить символами 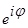 и
и 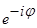 соответственно. Комбинируя эти формулы, можно получить формулы Эйлера:
соответственно. Комбинируя эти формулы, можно получить формулы Эйлера:
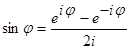 ,
, 
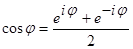 ,
,
Используя сокращённое обозначение, можно записать комплексное число в виде: 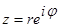 Такая форма называется показательной формой записи комплексного числа.
Такая форма называется показательной формой записи комплексного числа.
IV. Уравнение 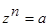 с натуральным
с натуральным 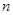 имеет ровно
имеет ровно 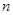 корней ( с учётом кратности). Если
корней ( с учётом кратности). Если
положить 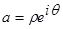 , то корни вычисляются по формуле:
, то корни вычисляются по формуле:
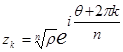 ,
, 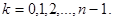 , являющейся аналогом формулы Муавра для
, являющейся аналогом формулы Муавра для
возведения в степень:
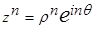
ТФКП 2 курс 4-ый семестр.
Задачи для решения в аудитории и домашнее задание.
- Проделать алгебраические действия с комплексными числами:
а) 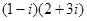 б)
б) 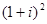 в)
в) 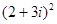
- Вычислить:
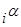 , если
, если 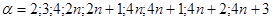
- Доказать формулу деления двух комплексных чисел
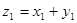 и
и 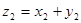 :
:
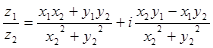
- Вычислить
 :
:  ,
, 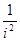 ,
, 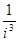 ,
, 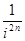 ,
, 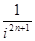 ,
, 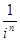 .
. - Вычислить
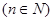 :
: 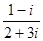 ,
, 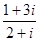 ,
, 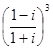 ,
, 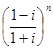 ,
, 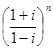
- Найти действительную и мнимую части следующих комплексных чисел:
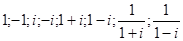
- Найти комплексно-сопряжённое число ко всем комплексным числам из задачи 6.
- Найти модуль всех комплексным числам из задачи 6.
- Найти модуль следующих комплексных чисел (
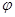 - действительное число):
- действительное число):
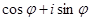 ;
; 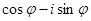 ;
; 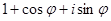 ;
; 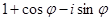 ;
; 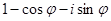 ;
;
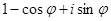 .
.
- Используя алгебраическую форму комплексного числа, доказать формулы:
а) 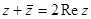 б)
б) 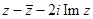 в)
в) 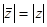 г)
г) 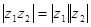 д)
д) 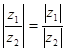
е) 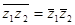 ж)
ж) 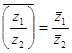 з)
з) 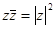
- Доказать формулы:
а) 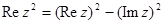 б)
б) 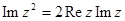 в)
в) 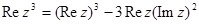
г) 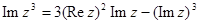 .
.
- Решить уравнения относительно z:
а) 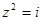 б)
б) 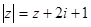 в)
в) 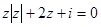 г)
г) 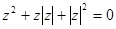
13. Указать на комплексной плоскости следующие числа, отметить их модуль и аргумент:
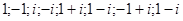
14. Нарисовать множества точек комплексной плоскости, которые удовлетворяют следующим
условиям ( 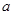 - комплексное число,
- комплексное число, 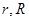 - действительные числа)
- действительные числа)
а) 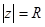 б)
б) 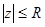 в)
в) 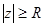 г)
г) 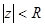 д)
д) 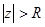 е)
е) 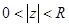 ж)
ж) 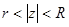
з) 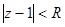 и)
и) 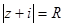 к)
к) 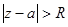 л)
л) 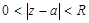 м)
м) 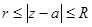
Регулярные (аналитические) функции
Необходимые сведения
1. Формулы для вычисления значений функций:
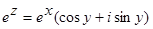 (1)
(1)
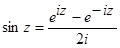 (2)
(2) 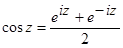 (3)
(3)
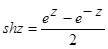 (4)
(4) 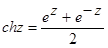 (5)
(5)
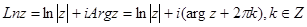 (6)
(6)
2. Условия Коши – Римана для функции
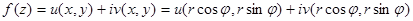 : (7)
: (7)
В декартовых координатах В полярных координатах
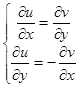 (8)
(8) 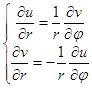 (9)
(9)
Задания для решения в аудитории
1.Вычислить: 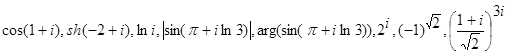
2.Выделить действительную и мнимую части следующих функций:
а) 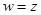 , б)
, б) 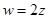 , в)
, в) 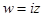 , г)
, г) 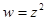 , д)
, д) 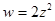 , е)
, е) 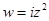 , ж)
, ж) 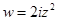
3. Выделить действительную и мнимую части следующих функций:
а) 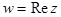 , б)
, б) 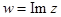 , в)
, в) 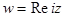 , г)
, г) 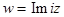 , д)
, д) 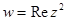 , е)
, е) 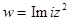
4. Выделить действительную и мнимую части следующих функций:
а) 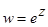 , б)
, б) 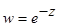 , в)
, в) 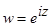 , г)
, г) 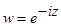 , д)
, д) 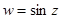 , е)
, е) 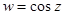 , ж)
, ж) 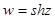
5.Доказать равенства:
а) 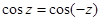 , б)
, б) 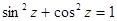 , в)
, в) 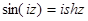
6.Вычислить:
а) 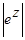 , б)
, б)  , в)
, в) 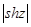
7.Найти все точки, в которых обращаются в нуль функции:
а) 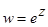 , б)
, б) 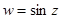 , в)
, в) 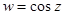 , г)
, г) 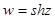 , д)
, д) 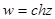 е)
е) 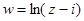
8.Найти все решения уравнений, изобразить решения на комплексной плоскости:
а) 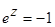 , б)
, б) 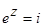 , в)
, в) 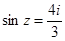 , г)
, г) 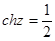
9.Найти значение модуля и главное значение аргумента заданных функций в указанных точках
а) 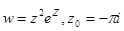 б)
б) 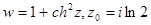
10.Проверить выполнение условий Коши – Римана :
а) 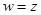 , б)
, б) 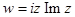 , в)
, в) 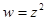 , г)
, г) 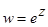 , д)
, д) 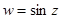 , е)
, е) 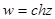 , ж)
, ж) 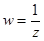
Домашнее задание
Ефимов-Поспелов, том 3: №№13.1 – 13.29
(Из них обязательно №№13.10,13.18, 13.23, 13.29),
№№13.35 – 13.41 (обязательно №№13.36, 13.39),
№№ 13.42 – 13.51 (обязательно №№13.44, 13.51)
Доказать равенства
а) 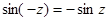 , б)
, б) 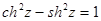 , в)
, в) 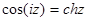 , г)
, г) 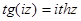 , д)
, д) 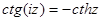
Вычислить:
а) 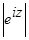 , б)
, б) 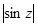 , в)
, в) 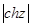
Доказать неравенства:
а) 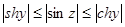 , б)
, б) 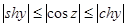
Найти все решения уравнений, изобразить решения на комплексной плоскости:
а) 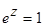 , б)
, б) 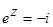 , в)
, в) 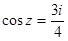 , г)
, г) 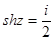
7.Проверить выполнение условий Коши – Римана :
а) 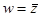 , б)
, б) 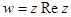 , в)
, в) 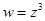 , г)
, г) 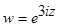 , д)
, д) 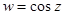 , е)
, е) 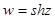 , ж)
, ж) 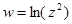
ЗАНЯТИЕ №2
Связь регулярных и гармонических функций.
Необходимые сведения
I. Утв.1. Если функция 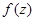 регулярна, то её действительная
регулярна, то её действительная 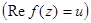 и мнимая
и мнимая 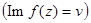 части – функции гармонические, т.е.
части – функции гармонические, т.е. 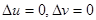
Утв.2. Если две функции 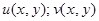 – гармонические и для них выполнены условия Коши – Римана:
– гармонические и для них выполнены условия Коши – Римана:
в декартовых координатах или в полярных координатах
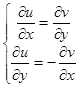 (1)
(1) 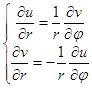 (2),
(2),
то эти две функции называются гармонически-сопряжёнными и они определяют регулярную функцию 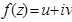 с точностью до комплексной константы.
с точностью до комплексной константы.
Таким образом, зная только действительную или только мнимую часть регулярной функции, можно восстановить эту функцию.
II. Если функция 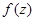 регулярна и
регулярна и 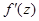 - её производная в точке
- её производная в точке 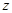 , то
, то
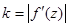 определяет коэффициент искажения длин в точке
определяет коэффициент искажения длин в точке 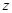 , а
, а 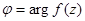 определяет угол поворота векторов в этой точке.
определяет угол поворота векторов в этой точке.
Если 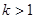 , то происходит растяжение
, то происходит растяжение 
Если 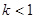 , то происходит сжатие
, то происходит сжатие
Если 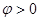 , то поворот против часовой стрелки
, то поворот против часовой стрелки
Если 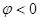 , то поворот по часовой стрелке
, то поворот по часовой стрелке
Задания для решения в аудитории
1.Восстановить регулярную функцию по её действительной части 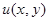 или по её мнимой части
или по её мнимой части 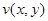 :
:
1.) 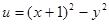
2.) 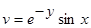
3.) 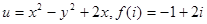
4.) 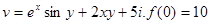
5.) 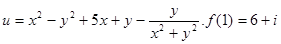 ,
, 
6.) 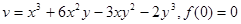
7.) 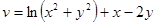
2.Существует ли регулярная функция 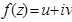 , для которой
, для которой 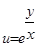 ?
?
3.Найти угол поворота лучей и коэффициент искажения длин
1)в точке 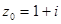 под действием отображения
под действием отображения 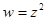
2)в точках 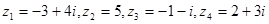 под действием отображения
под действием отображения 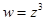 .
.
4.Какая часть плоскости сжимается, а какая растягивается, если отображение осуществляется функцией:
1.) 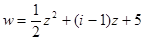 ?
?
2.) 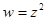 ?
?
3.) 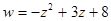 ?
?
4.) 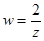 ?
?
5.) 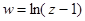 ?
?
6.) 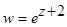 ?
?
(Изобразить на чертеже)
Домашнее задание
Ефимов-Поспелов, том 3: №№13.131 – 13.137, 13.138-13.143, 13.144-13.147 (изобразить полученные множества на комплексной плоскости), 13.148-13.155.
Конформные отображения.
Необходимые сведения
1.Отображение, осуществляемое линейной функцией 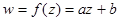 , представляет собой композицию
, представляет собой композицию
· растяжения ( в 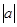 раз),
раз),
· поворота (на угол 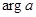 ),
),
· сдвига (параллельного переноса на 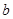 )
)
2.При отображении, осуществляемом степенной функцией 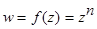 ,
,
· длины «возводятся в степень 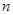 »,
»,
· углы «раскрываются в 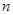 раз»
раз»
3.При отображении, осуществляемом показательной функцией 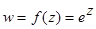
· прямые, параллельные действительной оси ( 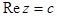 ), переходят в лучи (
), переходят в лучи ( 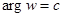 )
)
· отрезок прямой, параллельной мнимой оси ( 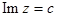 ), переходит в дугу окружности радиуса
), переходит в дугу окружности радиуса 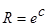
Таким образом, прямоугольник переходит в сектор кольца.
4. При отображении, осуществляемом главным значением логарифмической функции 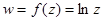 , происходит обратное, то есть
, происходит обратное, то есть
· окружности с центром в нуле ( 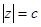 ) переходят в прямые
) переходят в прямые 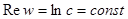
· лучи, выходящие из нуля ( 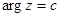 ), переходят в прямые
), переходят в прямые 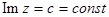
Отображение, осуществляемое сложной функцией, удобно рассматривать как композицию нескольких последовательных отображений.
Задания для решения в аудитории
Изобразить на комплексной плоскости множество 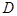 . Определить множество
. Определить множество 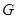 ,на которое отобразится
,на которое отобразится 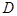 под действием отображения
под действием отображения 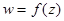 . Изобразить на комплексной плоскости множество
. Изобразить на комплексной плоскости множество 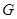 , описать его с помощью неравенств:
, описать его с помощью неравенств:
1) 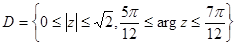 а)
а) 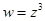 , б)
, б) 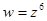 , в)
, в) 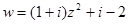
2) 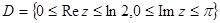 а)
а) 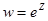 , б)
, б) 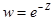 , в)
, в) 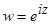
3) 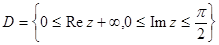 а)
а) 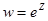 , б)
, б) 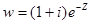 , в)
, в) 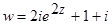
4) 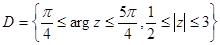 а)
а) 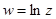 , б)
, б) 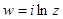 , в)
, в) 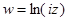
Домашнее задание
Ефимов-Поспелов, том 3: №№13.211 – 13.220.
Подготовиться к контрольной работе №1. Возможные постановки задач:
1)Изобразить ГМТ на плоскости.
2)Вычислить значение функции в данной точке.
3)Решить уравнение и изобразить его решения на компл. плоскости.
4)Проверить условия Коши-Римана для данной функции.
5)Восстановить регулярную функцию по её действ. или мним. части.
6)Найти образ данной области при заданном отображении
Занятие 3
Контрольная работа
Первая контрольная работа по ТФКП ориентирована на проверку знаний по темам занятий №№ 1 – 4
Примерные задания контрольной работы:
1. Проверить выполнение условий Коши-Римана для функции: 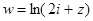
2. Вычислить 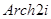
3. Решить уравнение и изобразить решения на комплексной плоскости: 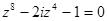
4. Восстановить регулярную функцию по её действительной части 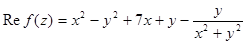 при условии:
при условии: 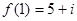
5. Найти образ множества 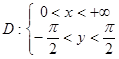 при отображении
при отображении 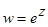 . Сделать соответствующие чертежи.
. Сделать соответствующие чертежи.
Для подготовки к контрольной работе рекомендуется решать задачи различных вариантов из Типового расчёта (№№1-4), а также задачи, указанные в листочках №№ 1 – 4
Результат контрольной работы (оценка) влияет на зачёт по Типовому расчёту, а он, в свою очередь, на допуск к экзамену.
Занятие 4
Необходимые сведения
· Для вычисления интеграла от функции 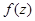 по кривой
по кривой 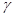 необходимо
необходимо
выбрать параметризацию кривой 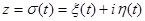 ,
, 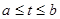 , после чего криволинейный интеграл сводится к определённому интегралу в соответствии с формулой:
, после чего криволинейный интеграл сводится к определённому интегралу в соответствии с формулой:
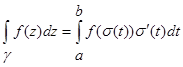
· Интегральная формула Коши для функции:
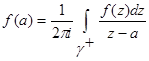
· Интегральная формула Коши для производной:
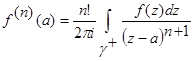
· При интегрировании многозначной функции необходимо выделять её однозначную ветвь.
Занятие 5
Комплексные ряды
Необходимые сведения
1. Функция, регулярная в круге 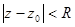 , раскладывается в ряд Тейлора:
, раскладывается в ряд Тейлора:
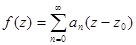
2. Функция, регулярная в кольце 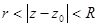 , раскладывается в ряд Лорана:
, раскладывается в ряд Лорана:
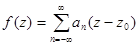 =
= 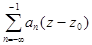 +
+ 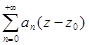
3. Для разложения функций в степенные ряды необходимо повторить разложение основных элементарных функций и формулу суммы бесконечно убывающей геометрической прогрессии (см. занятие 7 за 3 семестр)
Задания для решения в аудитории
1.Разложить функции в ряд по степеням z всеми возможными способами , указать области сходимости полученных рядов, изобразить их на плоскости С:
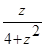 ;
; 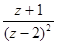 ;
; 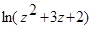 ;
; 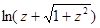
2.Разложить функции в ряд по степеням 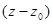 , определить области сходимости полученных рядов, изобразить их на плоскости С:
, определить области сходимости полученных рядов, изобразить их на плоскости С:
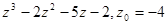 ;
; 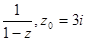 ;
; 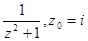 ;
; 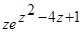 ,
, 
3.Найти области сходимости рядов, изобразить их на плоскости С:
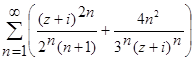 ,
, 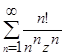
4.Найти все разложения функций в ряды Лорана по степеням 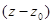 , установить области сходимости полученных разложений, сделать рисунок:
, установить области сходимости полученных разложений, сделать рисунок:
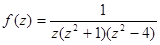 ,
, 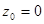 ;
; 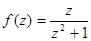 ,
, 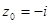
5.Найти разложение функции в ряд по степеням 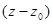 в указанной области:
в указанной области:
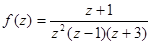 ;
; 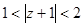
Домашнее задание
Ефимов-Поспелов, том 3:
№№13.226 – 13.229,
12.179, 12.181, 12.187 - 12.189.
12.217, 12.221, 12.226, 12.236, 12.241, 12.348, 12.350, 12.351.
12.352 – 12.375 (полезно сделать все, обязательно: любые 10 штук)
Занятие 6
Изолированные особые точки
Необходимые сведения
1. Точка 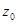 называется нулём функции
называется нулём функции 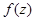 кратности
кратности 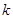 , если
, если 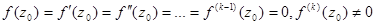
2. Точка 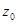 является нулём функции
является нулём функции 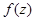 кратности
кратности 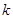
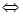 функция
функция
представима в виде 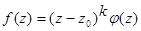 , где
, где 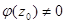
3. Точка, в которой функция не регулярна, называется особой точкой.
4. Если существует такая окрестность особой точки, в которой нет других особых точек, то эта особенность называется изолированной.
5. Изолированные особые точки можно разделить на три типа (см. таблицу)
Таблица: «Классификация особых точек»
| № |
Тип особой точки 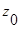
| Определение с помощью предела | Определение с помощью главной части ряда Лорана |
| 1 | Устранимая особая точка |
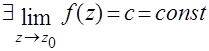
| Главная часть ряда Лорана отсутствует |
| 2 |
Полюс порядка 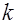
|
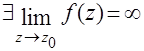
|
В главной части ряда Лорана конечное число слагаемых, максимальная отрицательная степень = 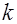
|
| 3 | Существенная особенность |
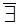 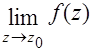 ни конечного, ни бесконечного
ни конечного, ни бесконечного
| В главной части ряда Лорана бесконечное число слагаемых |
6. Полюс первого порядка по-другому называют простым полюсом.
7. Связь между нулями и полюсами: если точка 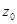 является нулём функции
является нулём функции 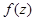 кратности
кратности 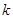 , то эта точка является полюсом порядка
, то эта точка является полюсом порядка 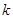 для функции
для функции 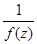
Задания для решения в аудитории
1. Определить все нули и их порядок для функций:
(а) 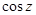 (б)
(б) 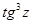 (в)
(в) 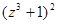 (г)
(г) 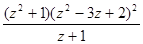
2. Найти все конечные особые точки, указать их характер, в случае полюса – его порядок , для функций:
(а) 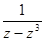 (б)
(б) 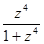 (в)
(в) 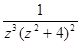 (г)
(г) 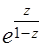 (д)
(д) 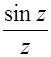 (е)
(е) 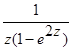
3. Определить характер особенности в точке 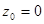 , разложив функцию
, разложив функцию 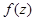 в ряд Лорана в окрестности этой точки и выделив главную часть полученного ряда:
в ряд Лорана в окрестности этой точки и выделив главную часть полученного ряда:
(а) 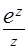 ;
; 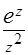 ;
; 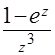 ;
; 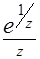 ;
; 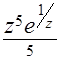 ;
; 
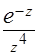
(б) 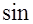 (
( 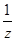 );
); 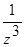
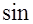 (
( 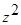 );
); 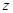
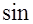
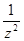 ;
; 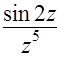 ;
; 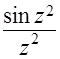
(в) 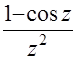 ;
; 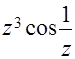 ;
; 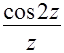 ;
; 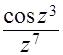 ;
; 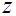
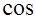
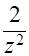
4. Исследовать поведение функции на бесконечности:
(а) 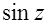 (б)
(б) 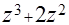 (в)
(в) 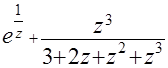
Домашнее задание
Определить все нули и их порядок для функций:
(а) 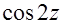 (б)
(б) 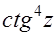 (в)
(в) 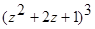 (г)
(г) 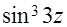
Ефимов-Поспелов, том 3: № № 12.382 – 12.407
Занятие 7
Вычеты
Применение вычетов
Необходимые сведения
1. Определение вычета: 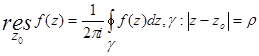
2. Отыскание вычета по ряду Лорана: 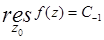 – коэффициент ряда Лорана в окрестности особой точки
– коэффициент ряда Лорана в окрестности особой точки 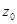
3. Вычисление вычета в простом полюсе:
(а) 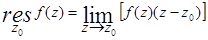
(б) Если 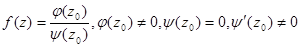 , тогда
, тогда 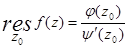
4. Вычисление вычета в кратном полюсе:
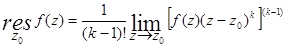
5. Основная теорема о вычетах: Если функция 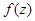 регулярна в ограниченной замкнутой области D за исключением конечного числа изолированных особых точек
регулярна в ограниченной замкнутой области D за исключением конечного числа изолированных особых точек 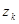 (k=1,…n), то интеграл по границе
(k=1,…n), то интеграл по границе 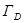 этой области вычисляется по формуле:
этой области вычисляется по формуле: 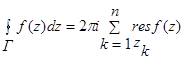
6. Вторая теорема о вычетах: сумма вычетов по всем особым точкам, считая бесконечно удалённую, равна нулю.
7. Алгоритм вычисления интеграла по замкнутому контуру с помощью вычетов:
· Контур интегрирования изобразить на плоскости
· Найти все особые точки подынтегральной функции (изобразить на плоскости)
· Отметить те точки , которые попадают внутрь контура интегрирования
· Определить их тип и найти вычеты в этих точках
· Просуммировать полученные вычеты и воспользоваться основной теоремой о вычетах
Задачи для решения в аудитории
1.Найти вычеты функций в особых конечных точках:
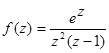 ;
; 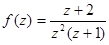 ;
; 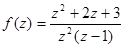 ;
;
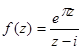 ;
; 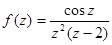 ;
; 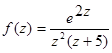 ;
;
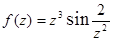 :
: 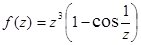 ;
; 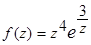 ;
; 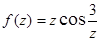
2.Определить характер бесконечно удалённой точки и найти вычет:
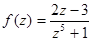 ;
; 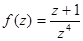 ;
; 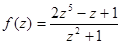 ;
;
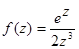 ;
; 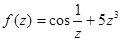 ;
; 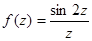 ;
;
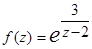 ;
; 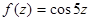 ;
; 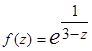 ;
;
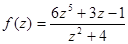 ;
; 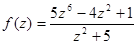 ;
; 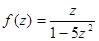 ;
;
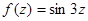 ;
; 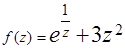 ;
; 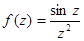 ;
; 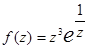 .
.
3.Вычислить интеграл:
a) 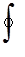
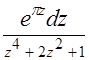 б)
б) 
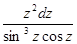 в)
в) 
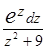
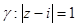
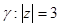
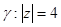
г) 
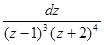 д)
д) 
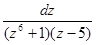 е)
е) 
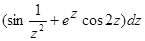
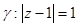
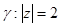
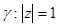
Домашнее задание
1. Ефимов, Поспелов, т.3, №№ 12.408 – 12.449
Занятие 8
Необходимые сведения
1. Интегралы вида
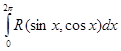 (1)
(1)
заменой 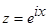 преобразуются в контурный интеграл по единичной окружности.
преобразуются в контурный интеграл по единичной окружности.
2. Интегралы вида
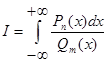 , (2)
, (2)
если 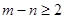 , а подынтегральная функция регулярна в верхней полуплоскости
, а подынтегральная функция регулярна в верхней полуплоскости 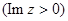 за исключением конечного числа особых точек, можно вычислить с помощью теоремы о вычетах:
за исключением конечного числа особых точек, можно вычислить с помощью теоремы о вычетах:
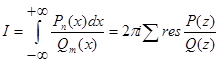 ,
,
где сумма вычетов берётся по всем особенностям, лежащим в верхней полуплоскости.
3. Интегралы вида
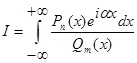 , (3)
, (3)
если 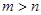 ,
, 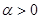 , подынтегральная функция регулярна в верхней полуплоскости кроме конечного числа особенностей, не имеет особенностей на действительной оси, можно вычислить с помощью теоремы о вычетах:
, подынтегральная функция регулярна в верхней полуплоскости кроме конечного числа особенностей, не имеет особенностей на действительной оси, можно вычислить с помощью теоремы о вычетах:
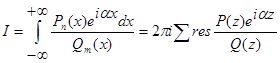 ,
,
где сумма вычетов берётся по всем особенностям, лежащим в верхней полуплоскости.
4. Интегралы вида 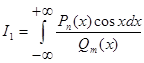 ,
, 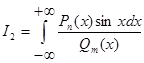
являются соответственно действительной и мнимой частями интеграла(3)
Занятие 9
Прием типового расчета
Занятие № 1
Комплексные числа.
Необходимые сведения.
I. Комплексным числом 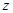 называется пара действительных чисел
называется пара действительных чисел 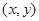 . Для комплексных чисел определено понятие равенства, сложения, умножения. Комплексные числа не сравниваются! Два комплексных числа
. Для комплексных чисел определено понятие равенства, сложения, умножения. Комплексные числа не сравниваются! Два комплексных числа 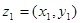 и
и 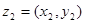 равны тогда и только тогда, когда
равны тогда и только тогда, когда 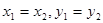 . Суммой двух комплексных чисел называется комплексное число
. Суммой двух комплексных чисел называется комплексное число 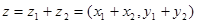 . Произведением двух комплексных чисел называется комплексное число
. Произведением двух комплексных чисел называется комплексное число 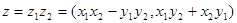 . Комплексное число (0,1) называется мнимой единицей и обозначается символом
. Комплексное число (0,1) называется мнимой единицей и обозначается символом 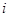 . Это число обладает свойством
. Это число обладает свойством 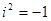 . Обычно комплексное число записывают в форме z= x+ iy. Эта запись называется алгебраической формой комплексного числа, причём
. Обычно комплексное число записывают в форме z= x+ iy. Эта запись называется алгебраической формой комплексного числа, причём 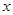 называется действительной частью и обозначается символом
называется действительной частью и обозначается символом 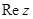 , а
, а 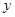 называется мнимой частью и обозначается символом
называется мнимой частью и обозначается символом 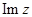 . Комплексное число
. Комплексное число 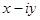 называется сопряжённым комплексному числу
называется сопряжённым комплексному числу 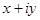 и обозначается символом
и обозначается символом 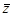 .Действительное положительное число
.Действительное положительное число 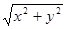 называется модулем комплексного числа и обозначается символом
называется модулем комплексного числа и обозначается символом 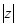 .
.
II. Комплексные числа можно изображать на плоскости.Каждое число z= x+ iy отождествляется с точкой плоскости с координатами 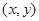 . Действительные числа отмечаются на оси абсцисс, поэтому её называют действительной осью, а чисто мнимые числа отмечаются на оси ординат, поэтому её называют мнимой осью. Комплексное число
. Действительные числа отмечаются на оси абсцисс, поэтому её называют действительной осью, а чисто мнимые числа отмечаются на оси ординат, поэтому её называют мнимой осью. Комплексное число 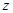
 изображается также вектором с началом в точке 0 и концом в точке
изображается также вектором с началом в точке 0 и концом в точке 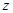 . Модуль комплексного числа имеет смысл длины этого вектора. Угол наклона вектора к положительному направлению действительной оси называется главным значением аргумента, он обозначается символом
. Модуль комплексного числа имеет смысл длины этого вектора. Угол наклона вектора к положительному направлению действительной оси называется главным значением аргумента, он обозначается символом 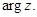
III. Любое комплексное число можно записать в виде 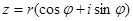 , где
, где 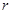 - модуль, а
- модуль, а 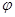 – аргумент комплексного числа. Такая форма называется тригонометрической формой записи комплексного числа. Комплексные числа
– аргумент комплексного числа. Такая форма называется тригонометрической формой записи комплексного числа. Комплексные числа 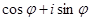 и
и 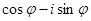 можно обозначить символами
можно обозначить символами 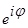 и
и 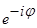 соответственно. Комбинируя эти формулы, можно получить формулы Эйлера:
соответственно. Комбинируя эти формулы, можно получить формулы Эйлера:
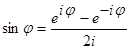 ,
, 
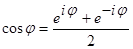 ,
,
Используя сокращённое обозначение, можно записать комплексное число в виде: 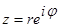 Такая форма называется показательной формой записи комплексного числа.
Такая форма называется показательной формой записи комплексного числа.
IV. Уравнение 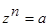 с натуральным
с натуральным 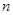 имеет ровно
имеет ровно 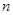 корней ( с учётом кратности). Если
корней ( с учётом кратности). Если
положить 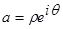 , то корни вычисляются по формуле:
, то корни вычисляются по формуле:
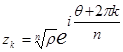 ,
, 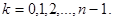 , являющейся аналогом формулы Муавра для
, являющейся аналогом формулы Муавра для
возведения в степень:
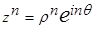
ТФКП 2 курс 4-ый семестр.
Задачи для решения в аудитории и домашнее задание.
- Проделать алгебраические действия с комплексными числами:
а) 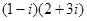 б)
б) 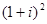 в)
в) 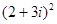
- Вычислить:
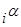 , если
, если 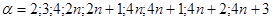
- Доказать формулу деления двух комплексных чисел
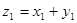 и
и 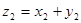 :
:
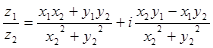
- Вычислить
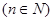 :
:  ,
, 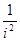 ,
, 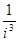 ,
, 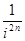 ,
, 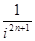 ,
, 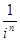 .
. - Вычислить
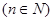 :
: 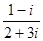 ,
, 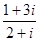 ,
, 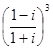 ,
, 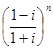 ,
, 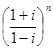
- Найти действительную и мнимую части следующих комплексных чисел:
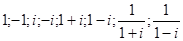
- Найти комплексно-сопряжённое число ко всем комплексным числам из задачи 6.
- Найти модуль всех комплексным числам из задачи 6.
- Найти модуль следующих комплексных чисел (
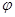 - действительное число):
- действительное число):
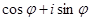 ;
; 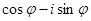 ;
; 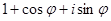 ;
; 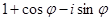 ;
; 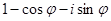 ;
;
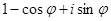 .
.
- Используя алгебраическую форму комплексного числа, доказать формулы:
а) 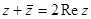 б)
б) 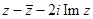 в)
в) 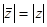 г)
г) 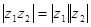 д)
д) 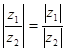
е) 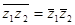 ж)
ж) 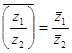 з)
з) 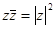
- Доказать формулы:
а) 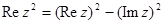 б)
б) 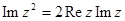 в)
в) 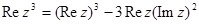
г) 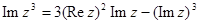 .
.
- Решить уравнения относительно z:
а) 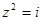 б)
б) 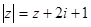 в)
в) 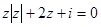 г)
г) 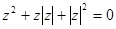
13. Указать на комплексной плоскости следующие числа, отметить их модуль и аргумент:
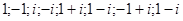
14. Нарисовать множества точек комплексной плоскости, которые удовлетворяют следующим
условиям ( 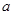 - комплексное число,
- комплексное число, 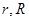 - действительные числа)
- действительные числа)
а) 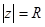 б)
б) 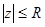 в)
в) 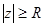 г)
г) 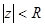 д)
д) 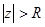 е)
е) 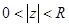 ж)
ж) 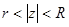
з) 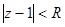 и)
и) 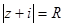 к)
к) 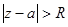 л)
л) 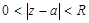 м)
м) 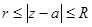
Регулярные (аналитические) функции
Необходимые сведения
1. Формулы для вычисления значений функций:
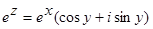 (1)
(1)
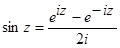 (2)
(2) 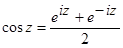 (3)
(3)
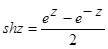 (4)
(4) 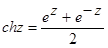 (5)
(5)
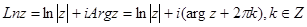 (6)
(6)
2. Условия Коши – Римана для функции
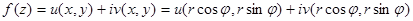 : (7)
: (7)
В декартовых координатах В полярных координатах
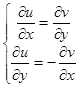 (8)
(8) 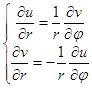 (9)
(9)
Задания для решения в аудитории
1.Вычислить: 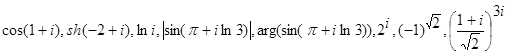
2.Выделить действительную и мнимую части следующих функций:
а) 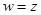 , б)
, б) 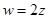 , в)
, в) 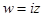 , г)
, г) 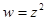 , д)
, д) 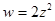 , е)
, е) 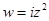 , ж)
, ж) 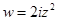
3. Выделить действительную и мнимую части следующих функций:
а) 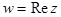 , б)
, б) 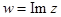 , в)
, в) 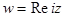 , г)
, г) 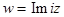 , д)
, д) 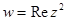 , е)
, е) 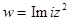
4. Выделить действительную и мнимую части следующих функций:
а) 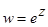 , б)
, б) 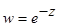 , в)
, в) 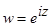 , г)
, г) 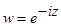 , д)
, д) 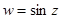 , е)
, е) 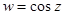 , ж)
, ж) 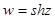
5.Доказать равенства:
а) 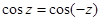 , б)
, б) 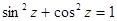 , в)
, в) 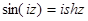
6.Вычислить:
а) 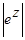 , б)
, б)  , в)
, в) 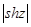
7.Найти все точки, в которых обращаются в нуль функции:
а) 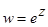 , б)
, б) 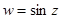 , в)
, в) 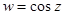 , г)
, г) 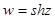 , д)
, д) 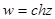 е)
е) 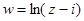
8.Найти все решения уравнений, изобразить решения на комплексной плоскости:
а) 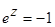 , б)
, б) 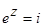 , в)
, в) 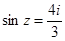 , г)
, г) 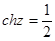
9.Найти значение модуля и главное значение аргумента заданных функций в указанных точках
а) 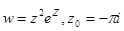 б)
б) 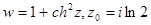
10.Проверить выполнение условий Коши – Римана :
а) 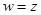 , б)
, б) 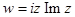 , в)
, в) 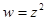 , г)
, г) 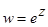 , д)
, д) 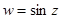 , е)
, е) 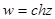 , ж)
, ж) 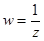
Домашнее задание
Ефимов-Поспелов, том 3: №№13.1 – 13.29
(Из них обязательно №№13.10,13.18, 13.23, 13.29),
№№13.35 – 13.41 (обязательно №№13.36, 13.39),
№№ 13.42 – 13.51 (обязательно №№13.44, 13.51)
Доказать равенства
а) 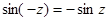 , б)
, б) 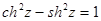 , в)
, в) 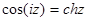 , г)
, г) 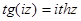 , д)
, д) 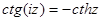
Вычислить:
а) 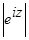 , б)
, б) 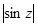 , в)
, в) 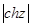
Доказать неравенства:
а) 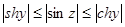 , б)
, б) 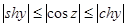
Найти все решения уравнений, изобразить решения на комплексной плоскости:
а) 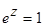 , б)
, б) 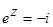 , в)
, в) 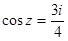 , г)
, г) 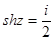
7.Проверить выполнение условий Коши – Римана :
а) 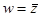 , б)
, б) 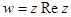 , в)
, в) 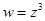 , г)
, г) 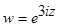 , д)
, д) 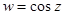 , е)
, е) 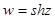 , ж)
, ж) 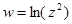
ЗАНЯТИЕ №2
Связь регулярных и гармонических функций.
Геометрический смысл модуля и аргумента производной регулярной функции.
Необходимые сведения
I. Утв.1. Если функция 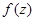 регулярна, то её действительная
регулярна, то её действительная 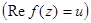 и мнимая
и мнимая 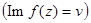 части – функции гармонические, т.е.
части – функции гармонические, т.е. 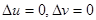
Утв.2. Если две функции 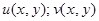 – гармонические и для них выполнены условия Коши – Римана:
– гармонические и для них выполнены условия Коши – Римана:
в декартовых координатах или в полярных координатах
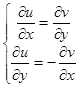 (1)
(1) 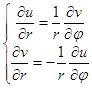 (2),
(2),
то эти две функции называются гармонически-сопряжёнными и они определяют регулярную функцию 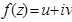 с точностью до комплексной константы.
с точностью до комплексной константы.
Таким образом, зная только действительную или только мнимую часть регулярной функции, можно восстановить эту функцию.
II. Если функция 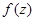 регулярна и
регулярна и 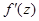 - её производная в точке
- её производная в точке 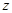 , то
, то
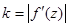 определяет коэффициент искажения длин в точке
определяет коэффициент искажения длин в точке 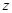 , а
, а 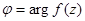 определяет угол поворота векторов в этой точке.
определяет угол поворота векторов в этой точке.
Если 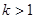 , то происходит растяжение
, то происходит растяжение 
Если 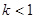 , то происходит сжатие
, то происходит сжатие
Если 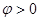 , то поворот против часовой стрелки
, то поворот против часовой стрелки
Если 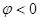 , то поворот по часовой стрелке
, то поворот по часовой стрелке
Задания для решения в аудитории
1.Восстановить регулярную функцию по её действительной части 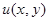 или по её мнимой части
или по её мнимой части 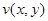 :
:
1.) 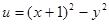
2.) 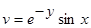
3.) 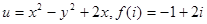
4.) 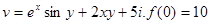
5.) 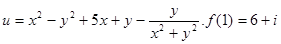 ,
, 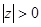
6.) 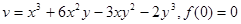
7.) 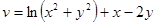
2.Существует ли регулярная функция 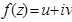 , для которой
, для которой 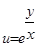 ?
?
3.Найти угол поворота лучей и коэффициент искажения длин
1)в точке 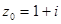 под действием отображения
под действием отображения 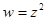
2)в точках 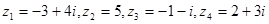 под действием отображения
под действием отображения 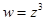 .
.
4.Какая часть плоскости сжимается, а какая растягивается, если отображение осуществляется функцией:
1.) 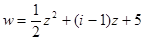 ?
?
2.) 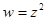 ?
?
3.) 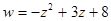 ?
?
4.) 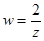 ?
?
5.) 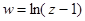 ?
?
6.) 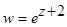 ?
?
(Изобразить на чертеже)
Домашнее задание
Ефимов-Поспелов, том 3: №№13.131 – 13.137, 13.138-13.143, 13.144-13.147 (изобразить полученные множества на комплексной плоскости), 13.148-13.155.
Конформные отображения.
Необходимые сведения
1.Отображение, осуществляемое линейной функцией 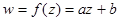 , представляет собой композицию
, представляет собой композицию
· растяжения ( в 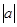 раз),
раз),
· поворота (на угол 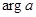 ),
),
· сдвига (параллельного переноса на 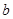 )
)
2.При отображении, осуществляемом степенной функцией 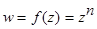 ,
,
· длины «возводятся в степень 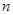 »,
»,
· углы «раскрываются в 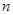 раз»
раз»
3.При отображении, осуществляемом показательной функцией 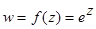
· прямые, параллельные действительной оси ( 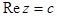 ), переходят в лучи (
), переходят в лучи ( 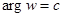 )
)
· отрезок прямой, параллельной мнимой оси ( 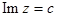 ), переходит в дугу окружности радиуса
), переходит в дугу окружности радиуса 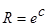
Таким образом, прямоугольник переходит в сектор кольца.
4. При отображении, осуществляемом главным значением логарифмической функции 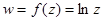 , происходит обратное, то есть
, происходит обратное, то есть
· окружности с центром в нуле ( 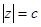 ) переходят в прямые
) переходят в прямые 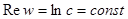
· лучи, выходящие из нуля ( 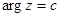 ), переходят в прямые
), переходят в прямые 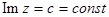
Отображение, осуществляемое сложной функцией, удобно рассматривать как композицию нескольких последовательных отображений.
Задания для решения в аудитории
Изобразить на комплексной плоскости множество 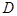 . Определить множество
. Определить множество 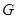 ,на которое отобразится
,на которое отобразится 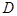 под действием отображения
под действием отображения 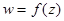 . Изобразить на комплексной плоскости множество
. Изобразить на комплексной плоскости множество 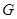 , описать его с помощью неравенств:
, описать его с помощью неравенств:
1) 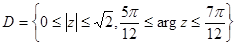 а)
а) 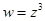 , б)
, б) 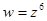 , в)
, в) 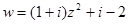
2) 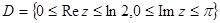 а)
а) 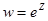 , б)
, б) 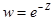 , в)
, в) 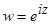
3) 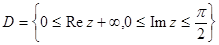 а)
а) 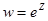 , б)
, б) 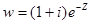 , в)
, в) 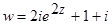
4) 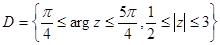 а)
а) 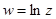 , б)
, б) 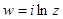 , в)
, в) 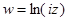
Домашнее задание
Ефимов-Поспелов, том 3: №№13.211 – 13.220.
Подготовиться к контрольной работе №1. Возможные постановки задач:
1)Изобразить ГМТ на плоскости.
2)Вычислить значение функции в данной точке.
3)Решить уравнение и изобразить его решения на компл. плоскости.
4)Проверить условия Коши-Римана для данной функции.
5)Восстановить регулярную функцию по её действ. или мним. части.
6)Найти образ данной области при заданном отображении
Занятие 3
Контрольная работа
Первая контрольная работа по ТФКП ориентирована на проверку знаний по темам занятий №№ 1 – 4
Примерные задания контрольной работы:
1. Проверить выполнение условий Коши-Римана для функции: 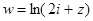
2. Вычислить 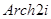
3. Решить уравнение и изобразить решения на комплексной плоскости: 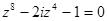
4. Восстановить регулярную функцию по её действительной части 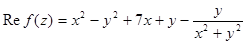 при условии:
при условии: 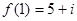
5. Найти образ множества 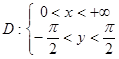 при отображении
при отображении 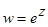 . Сделать соответствующие чертежи.
. Сделать соответствующие чертежи.
Для подготовки к контрольной работе рекомендуется решать задачи различных вариантов из Типового расчёта (№№1-4), а также задачи, указанные в листочках №№ 1 – 4
Результат контрольной работы (оценка) влияет на зачёт по Типовому расчёту, а он, в свою очередь, на допуск к экзамену.
Занятие 4
Дата: 2019-03-05, просмотров: 409.