Program Example_9;
Var k, n, znak : integer; S, sl, E : real;
Begin
writeln;
write(‘Введите количество слагаемых суммы N = ‘);
read(n);
write(‘Введите точность вычисления суммы Е = ‘);
read(Е);
S := 1;
znak :=-1;
For k := 2 to n do begin
S := S + znak*k / sqr(k + 14);
znak := - znak
end;
writeln(‘Вариант а) S = ’, S:6:4);
S := 0;
znak := 1;
k := 1;
sl :=1
while abs(sl) >= E do begin
S := S + znak * sl;
k := k + 1;
znak := - znak;
sl := k / sqr(k + 1)
end;
S := S + znak * sl;
writeln(‘Вариант б) S = ’, S:6:4);
readln
end.
Данные для тестирования
1) Для n = 3, Е = 0,2 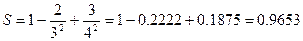
2) Для n = 4, Е = 0,17 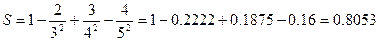
Пример 4.1 . Вычислить сумму ряда:
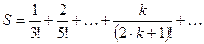
Решение задачи
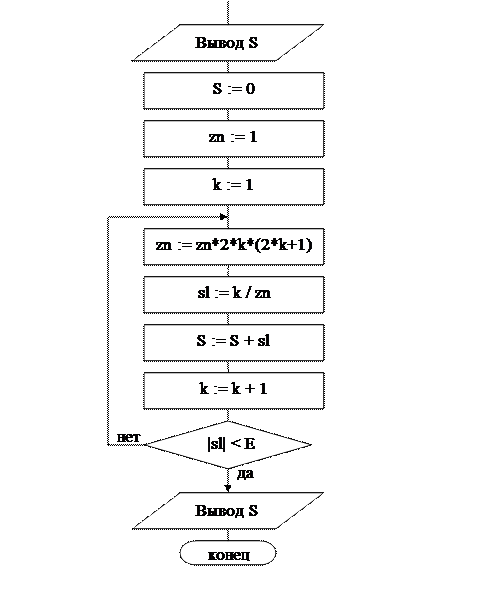
Выберем схему решения поставленной задачи.
Данная сумма может быть представлена в виде S=u1+u2+u3+u4+….
Начальное значение суммы S=1.
При вычислении суммы к начальному ее значению прибавляется значение первого члена последовательности, затем к полученному значению прибавляется значение второго члена последовательности и так далее. То есть при вычислении суммы циклически проводится операция сложения.
При расчете абсолютного значения дроби надо отметить закономерность:
· Числитель очередного слагаемого равен порядковому номеру члена суммы (обозначим его переменной k).
· Знаменатель очередной дроби (обозначим его zn) можно получить путём умножения знаменателя предыдущей дроби на выражение 2*k*(2*k+1). При этом необходимо задать начальное значение zn = 1.
В варианте а) число членов суммы заранее известно (равно N), и для решения задачи удобно использовать цикл с параметром.
В варианте б) значение очередного слагаемого следует запомнить в некоторой переменной (sl), чтобы использовать его при проверке условия прекращения вычислений – модуль последнего слагаемого должен быть меньше заданной величины e.
Вычисление суммы в варианте б) организуем с помощью цикла repeat: до тех пор пока очередное слагаемое по модулю не станет меньше e (в алгоритме обозначим её Е), будем выполнять действия в цикле. После завершения цикла искомая сумма будет вычислена.
Блок-схема алгоритма
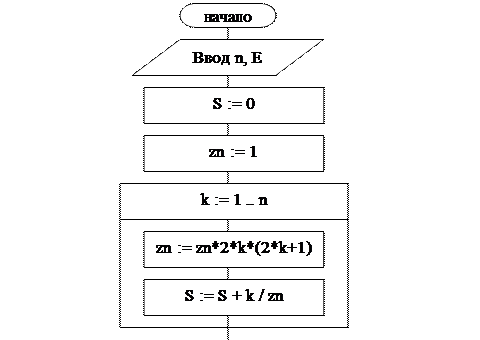
Текст программы на языке Паскаль
Program Example_10;
Var k, n, zn : word; S, sl, E : real;
Begin
writeln;
write(‘Введите количество слагаемых суммы N = ‘);
read(n);
write(‘Введите точность вычисления суммы Е = ‘);
read(Е);
S := 0;
zn := 1;
For k := 1 to n do begin
zn := zn*2*k*(2*k+1);
S := S + k / zn
end;
writeln(‘Вариант а) S = ’, S:6:4);
S := 0;
zn := 1;
k := 1;
repeat
zn := zn*2*k*(2*k+1);
sl := k / zn
S := S + sl;
k := k + 1;
until abs(sl) < E;
writeln(‘Вариант б) S = ’, S:6:4);
readln
end.
Данные для тестирования
1) Для n = 3, Е = 0,0002
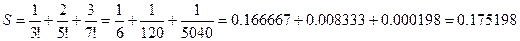
2) Для n = 2, Е = 0,01 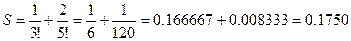
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
В задачах этой темы для заданного действительного x необходимо вычислить значение суммы S(x).
Каждая задача должна решаться в двух вариантах:
а) задано число членов суммы N;
б) вычисление производить до тех пор, пока очередной член вычисляемой суммы не станет по модулю меньше заданного значения e. Все последующие слагаемые в S входить не должны.
При решении задач данной темы для реализации варианта а) должен использоваться оператор цикла с параметром (for), а для реализации варианта б) – оператор цикла с постусловием (repeat) или оператор цикла с предусловием (while) – это (как и для задач предыдущей темы) определяет конкретный преподаватель.
Принципы решения задач из этой темы такие же, как и для вычисления числовых рядов. Отличие их состоит лишь в том, что в качестве исходных данных появляется ещё действительная переменная х, значение которой следует подбирать таким, чтобы при проверке расчеты оказались не слишком сложными, и каждое следующее слагаемое ряда было по модулю меньше предыдущего.
Пример 5.1 . Вычислить сумму ряда:
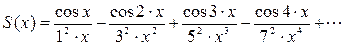
Решение задачи
Выберем схему решения поставленной задачи.
Данная сумма может быть представлена в виде S=u1-u2+u3-u4+….
Начальное значение суммы равно 0.
При вычислении суммы к начальному ее значению прибавляется значение первого члена последовательности, затем из полученного значения вычитается значение второго члена последовательности, затем прибавляется значение третьего члена, затем вычитается значение четвертого члена суммы и так далее. То есть при вычислении суммы необходимо учитывать чередование знака слагаемых.
Для учета такого чередования введём дополнительную переменную Znak, которая будет принимать значения либо 1, либо –1. Начальное значение знака
Znak=1. Чередование значений переменной будем получать циклическим умножением переменной на –1, то есть проводить вычисления по формуле 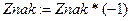 .
.
При вычислении значения суммы надо к предыдущему значению суммы прибавить значение модуля очередного слагаемого, умноженного на знак.
При расчете абсолютного значения дроби надо отметить закономерность:
· Числитель очередного слагаемого представляет собой стандартную функцию cos, аргументом которой является произведение порядкового номера члена суммы (обозначим его переменной k) на переменную х, то есть cos ( k * x ).
· Знаменатель очередной дроби можно представить в виде произведения двух сомножителей: квадрата выражения (2* k -1) и очередной степени переменной х (обозначим эту часть переменной st), которую можно получить путём умножения значения st предыдущей дроби на x. Зададим начальное значение st = 1.
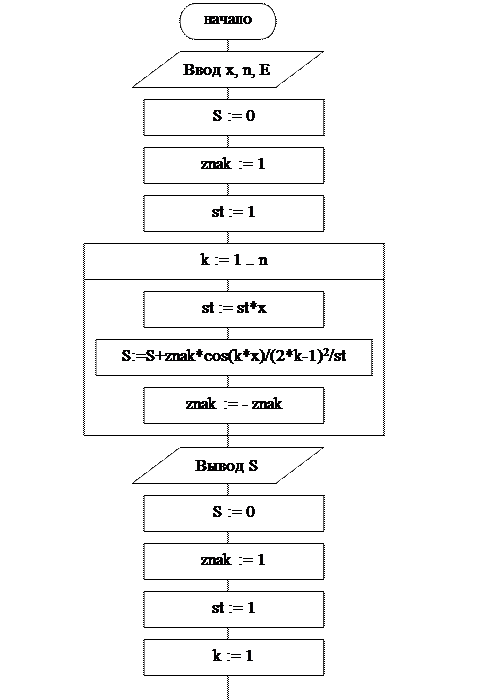
В варианте а) число членов суммы заранее известно (равно N), и для решения задачи удобно использовать цикл с параметром.
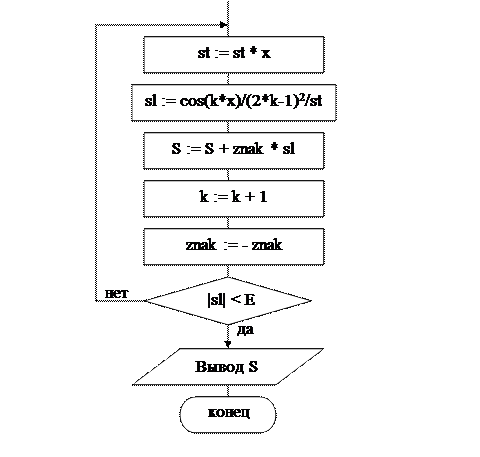
В варианте б) значение очередного слагаемого следует запомнить в некоторой переменной (sl), чтобы использовать его при проверке условия прекращения вычислений – модуль последнего слагаемого должен быть меньше заданной величины e.
Вычисление суммы в варианте б) организуем с помощью цикла repeat: до тех пор пока очередное слагаемое по модулю не станет меньше e (в алгоритме обозначим её Е), будем выполнять действия в цикле. После завершения цикла искомая сумма будет вычислена.
Блок-схема алгоритма
Дата: 2019-03-05, просмотров: 351.