Новоуральский технологический институт
Кафедра информатики и программирования
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПО ПРОГРАММИРОВАНИЮ
Часть 1
Учебно-методическое пособие по курсам
«Информатика», «Программирование и основы алгоритмизации»,
«Программирование на языках высокого уровня»
для студентов всех специальностей
очной формы обучения
Новоуральск 2010
УДК 681.3.06
МиМ – 2.3. - - 10
Автор Орлова Ирина Викторовна
Рецензент кандидат физико-математических наук, доцент кафедры ВМ Фоминых Марина Анатольевна
Примеры решения задач по программированию. Часть 1. Учебно-методическое пособие по курсам «Информатика», «Программирование и основы алгоритмизации», «Программирование на языках высокого уровня» для студентов всех специальностей очной формы обучения
Новоуральск, НТИ НИЯУ МИФИ, 2010, 56 с.
Пособие представляет собой описание решения 21 задачи по программированию на языке Паскаль по основным девяти темам, изучаемым в курсах «Информатика», «Программирование и основы алгоритмизация» и «Программирование на языках высокого уровня» в НТИ НИЯУ МИФИ.
Содержит 21 библиографических названия.
Пособие может использоваться при самостоятельном изучении программирования на языке Паскаль».
Методическое пособие рассмотрено на заседании кафедры
Протокол № 117 от 21 июня 2010 г.
Зав.кафедрой Н.А.Николаев
СОГЛАСОВАНО:
Председатель методкомиссии НТИ НИЯУ МИФИ
д.т.н., профессор А.Е.Беляев
Оглавление
ВВедение.. 4
1 ОПЕРАТОР ПРИСВАИВАНИЯ.. 5
2 УСЛОВНЫЙ ОПЕРАТОР.. 8
3 ПРОСТЕЙШИЕ ЦИКЛЫ... 13
4 ЧИСЛОВЫЕ РЯДЫ... 19
5 ФУНКЦИОНАЛЬНЫЕ РЯДЫ... 25
6 ЗАДАЧИ С ИСПОЛЬЗОВАНИЕМ МАССИВОВ.. 29
7 ВЛОЖЕННЫЕ ЦИКЛЫ... 35
8 ПРОЦЕДУРЫ И ФУНКЦИИ.. 40
9 работа с МАТРИЦами.. 47
Список литературы... 54
ВВедение
Студенты НТИ НИЯУ МИФИ различных специальностей изучают программирование в курсах "Программирование на языке высокого уровня", "Программирование и основы алгоритмизации" и "Информатика" в разных объёмах, но в любом случае основой изучения данной темы является лабораторный практикум, который структурно делится на две части: общий практикум, сопровождающий основной курс по программированию, и практикум по численным методам, нацеленный на приобретение студентами опыта решения на ЭВМ определенных классов задач, а также на практическое освоение студентами специализированных компонент математического обеспечения.
Каждая задача практикума – это самостоятельная задача с краткой, но четкой содержательной формулировкой, не содержащей описания алгоритма. В процессе решения задачи от студента требуется:
- составить алгоритм решения задачи;
- записать алгоритм в виде программы на Паскале;
- произвести отладку программы;
- протестировать программу по заранее подготовленным данным;
Первый и второй этапы выполняются дома при подготовке к лабораторной работе, третий и четвертый - во время лабораторной работы.
Студентам, только начинающим изучать основы алгоритмизации и программирование, а также имеющим не достаточно глубокие знания элементарной математики, математического анализа и линейной алгебры, бывает трудно представить ход решения предлагаемых задач и правильно оформить отчёт к лабораторной работе по программированию.
В данном пособии рассматриваются примеры решения задач по первой, общей части практикума. Представленные в пособии задачи сгруппированы по девяти темам, которые соответствуют темам лабораторных работ, задания для которых содержатся в методическом пособии [3] и практически полностью охватывают материал, изучаемый студентами всех специальностей в первом семестре изучения соответствующего курса.
На каждую тему в данном пособии приводится по 2–3 примера, которые подобраны так, чтобы рассмотреть наиболее часто используемые приёмы при решении задач указанной темы. Для каждой из рассматриваемых задач, помимо условия, приводится математическая модель или описание рассуждений, используемых при решении задачи, затем приводится блок-схема алгоритма, текст программы на языке Паскаль и данные для тестирования, с помощью которых можно проверить правильность работы представленной программы.
Настоящее пособие может быть использовано студентами при подготовке к лабораторным и контрольным работам или изучающими самостоятельно тему «Основы алгоритмизации и программирования на языке Паскаль», преподавателями при подготовке и проведении лекций по этой теме в курсах «Информатика», «Программирование и основы алгоритмизации» и «Программирование на языках высокого уровня», а также сотрудниками, которые в своей работе встречаются с необходимостью составления алгоритмов и написания программ на языке Паскаль.
ОПЕРАТОР ПРИСВАИВАНИЯ
В этом разделе рассматриваются примеры решения простейших задач, алгоритм которых имеет линейную структуру. По каждой задаче составлена программа, содержащая операторы ввода исходных данных, присваивания и вывода результатов. В программах предусмотрен вывод подсказки для ввода и пояснения результата при выводе.
Пример 1.1. Дано натуральное трехзначное число. Вычислить сумму его цифр.
Блок-схема алгоритма
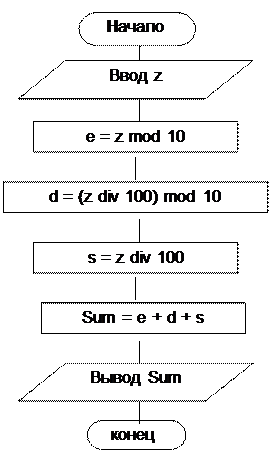
Данные для тестирования
1) Для числа z=128 – сумма цифр = 1 + 2 + 8 = 11
2) Для числа z=756 – сумма цифр = 7 + 5 + 6 = 18
Пример 1.2 . Даны два круга с общим центром и радиусами R1 и R2 (R1 > R2 ). Найти площадь S кольца, внешний радиус которого равен R1 , а внутренний радиус R2. В качестве значения π использовать 3.14.
Блок-схема алгоритма
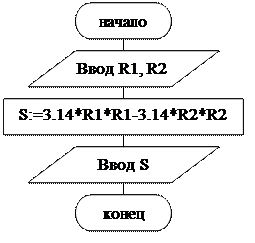
Данные для тестирования
1) Для R1=5, R2=3 – Площадь кольца S = 3.14*52 – 3.14*32 = 50.24
2) Для R1=7, R2=5 – Площадь кольца S = 3.14*72 – 3.14*52 = 75.36
УСЛОВНЫЙ ОПЕРАТОР
В этом разделе рассматривается решение задач с использованием условного оператора. В некоторых задачах решение будет более компактным и простым если при проверке условия составить сложное логическое выражение, а в других задачах необходимо использовать вложенный оператор if.
Пример 2.1 . Даны действительные числа x, y. Меньшее из этих двух чисел заменить их удвоенной суммой, а большее – половиной их произведения. Если числа равны, то оставить их без изменения.
Математическая модель задачи
Введём переменные:
min = 2*(x + y);
max = x * y / 2.
Блок-схема алгоритма
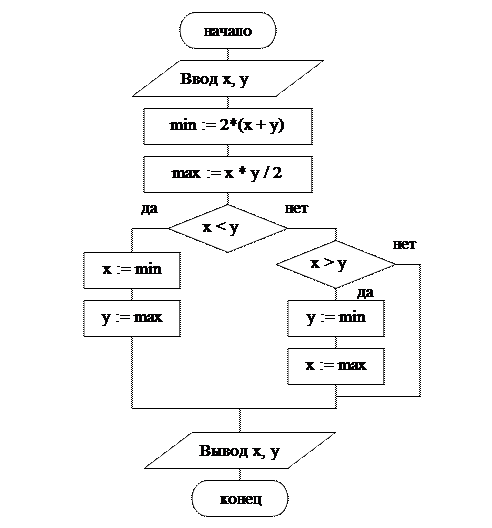
Данные для тестирования
1) Для x = 5, y = 3 ð min = 2*(5+3) = 16; max = 5 * 3 / 2 = 7.5;
Результат: x = 7.5 y = 16
2) Для x = 3, y = 5 ð min = 2*(3+5) = 16; max = 3 * 5 / 2 = 7.5;
Результат: x = 16 y = 7.5
3) Для x = 3, y = 3 ð Результат: x = 3 y = 3
Пример 2.2 . Даны два действительных числа x, y. Определить, принадлежит ли точка с координатами x, y заштрихованной области.
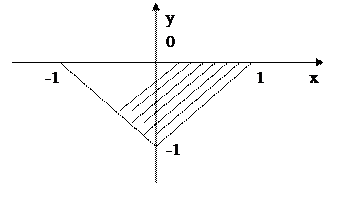
Блок-схема алгоритма
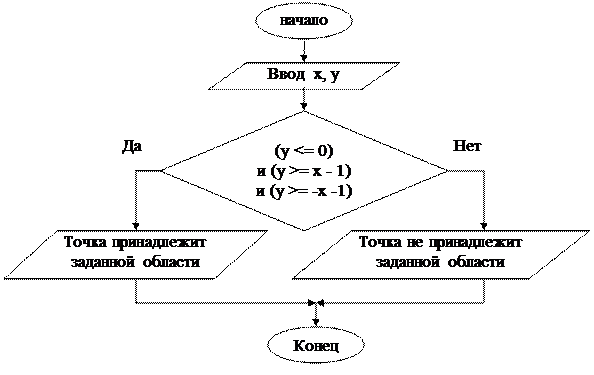
Данные для тестирования
1) Для x = -0.3, y = -0.6 ð Точка принадлежит заштрихованной области;
2) Для x = -0.3, y = -1 ð Точка не принадлежит заштрихованной области;
3) Для x = 0.6, y = -0.3 ð Точка принадлежит заштрихованной области;
4) Для x = 0.3, y = 1 ð Точка не принадлежит заштрихованной области;
Пример 2.3 . Дано действительное число a. Для функции f(x), график которой представлен на рисунке, вычислить значение f(a).
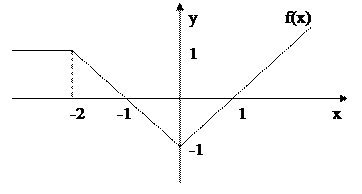
Блок-схема алгоритма
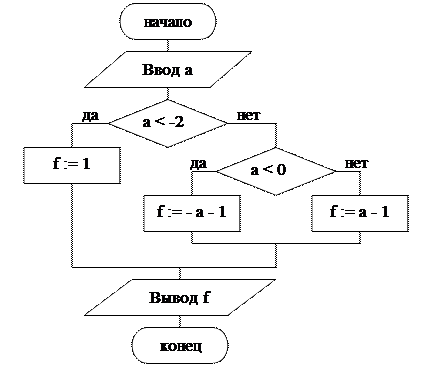
Данные для тестирования
1) Для a = -4 ð Результат: f(-4.00) = 1.00
2) Для a = -1.3 ð Результат: f(-1.30) = 0.30
3) Для a = 2.7 ð Результат: f(2.70) = 1.70
ПРОСТЕЙШИЕ ЦИКЛЫ
При решении задач этой темы используются алгоритмы, имеющие циклическую структуру. В зависимости от последовательности рассмотрения материала (операторов цикла), предполагается, что для реализации решения на языке Паскаль могут использоваться оператор цикла с предусловием while или оператор цикла с постусловием repeat.
Пример 3.1 . Даны натуральные числа А, В. Найти наименьшее общее кратное этих двух чисел.
Блок-схема алгоритма
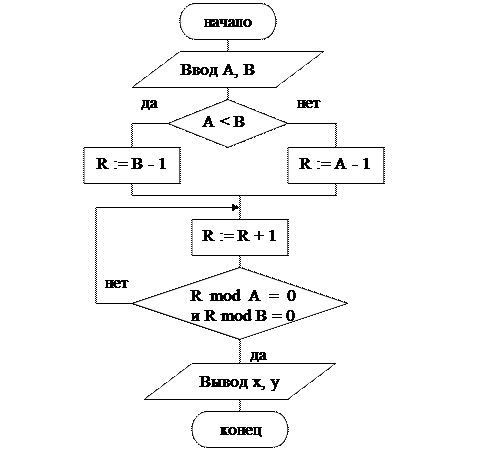
Данные для тестирования
1) Для А = 5, В = 3
ð 15 - наименьшее общее кратное чисел 5 и 3
2) Для А = 5, В = 30
ð 30 - наименьшее общее кратное чисел 5 и 30
3) Для А = 10, В = 25
ð 50 - наименьшее общее кратное чисел 10 и 25
Пример 3.2 . Найти наибольшее и наименьшее значение функции y = 3x2 + x – 4, если на заданном отрезке [А, В] значения х изменяются с шагом 0,1.
Блок-схема алгоритма
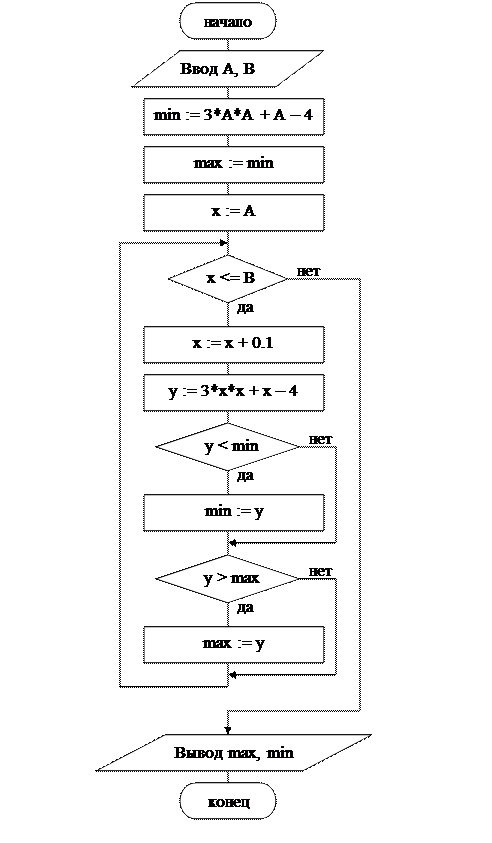
Данные для тестирования
| x | y |
| А = -1 |
|
|
| -1 | -2 |
| В = 1 |
|
|
| -0,9 | -2,47 |
|
|
|
|
| -0,8 | -2,88 |
|
|
|
|
| -0,7 | -3,23 |
|
|
|
|
| -0,6 | -3,52 |
|
|
|
|
| -0,5 | -3,75 |
|
|
|
|
| -0,4 | -3,92 |
|
|
|
|
| -0,3 | -4,03 |
|
|
|
|
| -0,2 | -4,08 | - наименьшее значение функции | |||
| -0,1 | -4,07 |
|
|
|
|
| 0 | -4 |
|
|
|
|
| 0,1 | -3,87 |
|
|
|
|
| 0,2 | -3,68 |
|
|
|
|
| 0,3 | -3,43 |
|
|
|
|
| 0,4 | -3,12 |
|
|
|
|
| 0,5 | -2,75 |
|
|
|
|
| 0,6 | -2,32 |
|
|
|
|
| 0,7 | -1,83 |
|
|
|
|
| 0,8 | -1,28 |
|
|
|
|
| 0,9 | -0,67 |
|
|
|
|
| 1 | 0 | - наибольшее значение функции | |||
Пример 3.3 . Дано натуральное n. Вычислить сумму
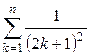
Решение задачи
Введём переменные: S – сумма;
k – номер очередного слагаемого;
n– количество слагаемых в сумме.
Данная сумма может быть представлена в виде S=u1+u2+u3+… .
Начальное значение суммы равно 0.
При вычислении суммы к начальному ее значению прибавляется значение первого члена последовательности, затем к полученному значению прибавляется значение второго члена последовательности и так далее. То есть при вычислении суммы циклически проводится операция сложения.
Вычисление суммы организуем с помощью цикла while . Если до начала цикла k присвоить 1, то в качестве условия выполнения цикла можно записать k <= n.
Блок-схема алгоритма
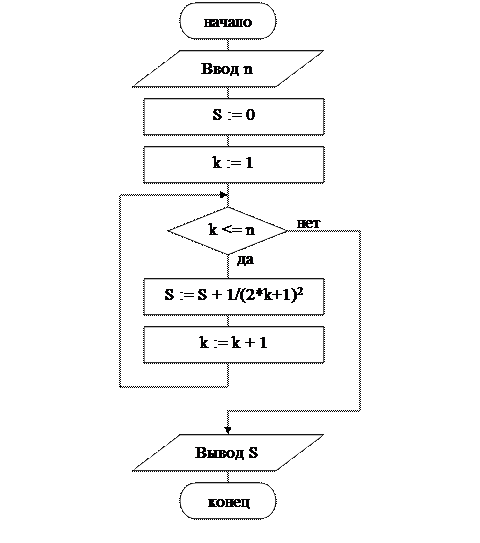
Данные для тестирования
1) Для n = 2 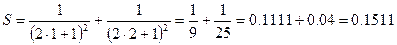
2) Для n = 3
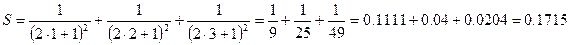
ЧИСЛОВЫЕ РЯДЫ
В задачах этой темы необходимо вычислить заданные суммы S.
Каждая задача должна решаться в двух вариантах:
а) задано число членов суммы N;
б) вычисление производить до тех пор, пока очередной член вычисляемой суммы не станет по модулю меньше заданного значения e . Все последующие слагаемые в S входить не должны.
При решении задач данной темы для реализации варианта а) должен использоваться оператор цикла с параметром (for), а для реализации варианта б) – оператор цикла с постусловием (repeat) или оператор цикла с предусловием (while) – это определяет конкретный преподаватель.
Пример 4.1 . Вычислить сумму ряда:
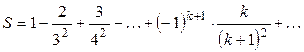
Решение задачи
Выберем схему решения поставленной задачи.
Данная сумма может быть представлена в виде S=u1-u2+u3-u4+….
Начальное значение суммы – это первое слагаемое u1=1.
При вычислении суммы из начального ее значения вычитается значение второго члена последовательности, затем прибавляется значение третьего члена, затем вычитается значение четвертого члена суммы и так далее. То есть при вычислении суммы необходимо учитывать чередование знака слагаемых.
Для учета такого чередования надо ввести дополнительную переменную Znak, которая будет принимать значения либо 1, либо –1. Начальное значение знака
Znak=-1. Чередование значений переменной можно получить циклическим умножением переменной на –1, то есть проводить вычисления по формуле 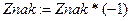 .
.
При вычислении значения суммы надо к предыдущему значению суммы прибавить значение модуля очередного слагаемого, умноженного на знак.
При расчете абсолютного значения дроби надо отметить закономерность. Числитель очередного слагаемого равен порядковому номеру члена суммы (обозначим его переменной k). Тогда знаменатель дроби можно рассчитать по формуле (k + 1)2.
В варианте а) число членов суммы заранее известно (равно N), и для решения задачи удобно использовать цикл с параметром.
В варианте б) значение очередного слагаемого следует запомнить в некоторой переменной (sl), чтобы использовать его при проверке условия прекращения вычислений – модуль последнего слагаемого должен быть меньше заданной величины e.
Вычисление суммы в варианте б) организуем с помощью цикла while: пока очередное слагаемое по модулю будет больше e (в алгоритме обозначим её Е), будем выполнять действия в цикле. Чтобы не «потерять» последнее слагаемое, прибавим его к сумме после завершения цикла
|
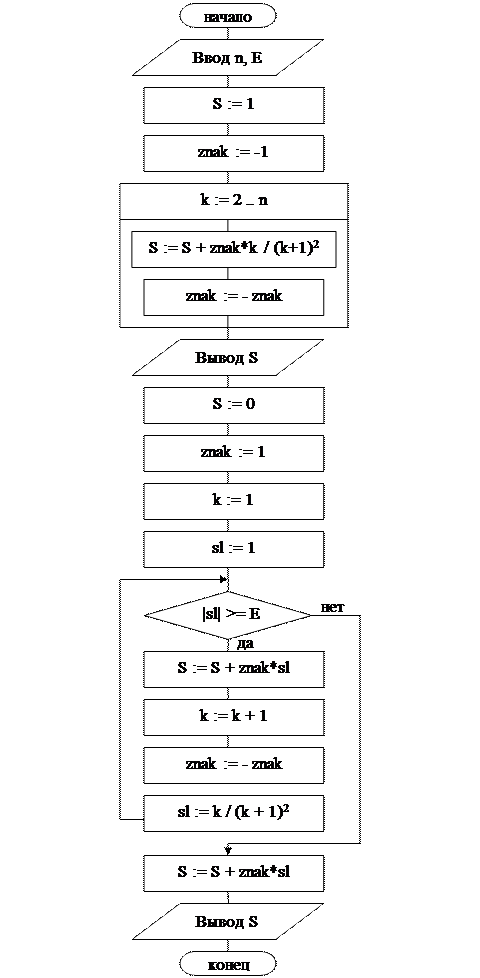
Данные для тестирования
1) Для n = 3, Е = 0,2 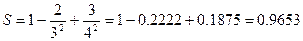
2) Для n = 4, Е = 0,17 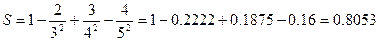
Пример 4.1 . Вычислить сумму ряда:
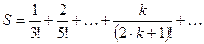
Решение задачи
Выберем схему решения поставленной задачи.
Данная сумма может быть представлена в виде S=u1+u2+u3+u4+….
Начальное значение суммы S=1.
При вычислении суммы к начальному ее значению прибавляется значение первого члена последовательности, затем к полученному значению прибавляется значение второго члена последовательности и так далее. То есть при вычислении суммы циклически проводится операция сложения.
При расчете абсолютного значения дроби надо отметить закономерность:
· Числитель очередного слагаемого равен порядковому номеру члена суммы (обозначим его переменной k).
· Знаменатель очередной дроби (обозначим его zn) можно получить путём умножения знаменателя предыдущей дроби на выражение 2*k*(2*k+1). При этом необходимо задать начальное значение zn = 1.
В варианте а) число членов суммы заранее известно (равно N), и для решения задачи удобно использовать цикл с параметром.
В варианте б) значение очередного слагаемого следует запомнить в некоторой переменной (sl), чтобы использовать его при проверке условия прекращения вычислений – модуль последнего слагаемого должен быть меньше заданной величины e.
Вычисление суммы в варианте б) организуем с помощью цикла repeat: до тех пор пока очередное слагаемое по модулю не станет меньше e (в алгоритме обозначим её Е), будем выполнять действия в цикле. После завершения цикла искомая сумма будет вычислена.
Блок-схема алгоритма
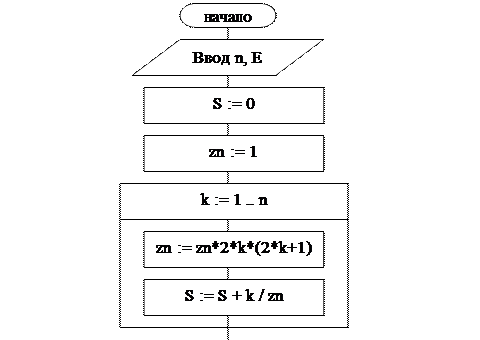
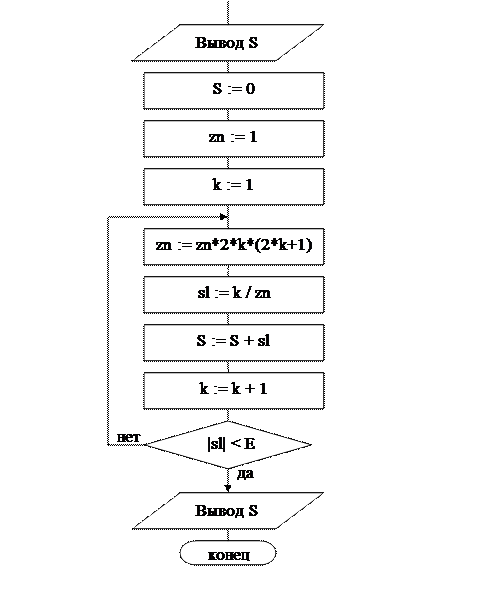
Данные для тестирования
1) Для n = 3, Е = 0,0002
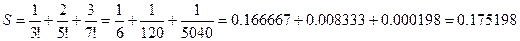
2) Для n = 2, Е = 0,01 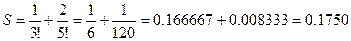
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
В задачах этой темы для заданного действительного x необходимо вычислить значение суммы S(x).
Каждая задача должна решаться в двух вариантах:
а) задано число членов суммы N;
б) вычисление производить до тех пор, пока очередной член вычисляемой суммы не станет по модулю меньше заданного значения e. Все последующие слагаемые в S входить не должны.
При решении задач данной темы для реализации варианта а) должен использоваться оператор цикла с параметром (for), а для реализации варианта б) – оператор цикла с постусловием (repeat) или оператор цикла с предусловием (while) – это (как и для задач предыдущей темы) определяет конкретный преподаватель.
Принципы решения задач из этой темы такие же, как и для вычисления числовых рядов. Отличие их состоит лишь в том, что в качестве исходных данных появляется ещё действительная переменная х, значение которой следует подбирать таким, чтобы при проверке расчеты оказались не слишком сложными, и каждое следующее слагаемое ряда было по модулю меньше предыдущего.
Пример 5.1 . Вычислить сумму ряда:
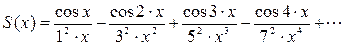
Решение задачи
Выберем схему решения поставленной задачи.
Данная сумма может быть представлена в виде S=u1-u2+u3-u4+….
Начальное значение суммы равно 0.
При вычислении суммы к начальному ее значению прибавляется значение первого члена последовательности, затем из полученного значения вычитается значение второго члена последовательности, затем прибавляется значение третьего члена, затем вычитается значение четвертого члена суммы и так далее. То есть при вычислении суммы необходимо учитывать чередование знака слагаемых.
Для учета такого чередования введём дополнительную переменную Znak, которая будет принимать значения либо 1, либо –1. Начальное значение знака
Znak=1. Чередование значений переменной будем получать циклическим умножением переменной на –1, то есть проводить вычисления по формуле 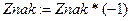 .
.
При вычислении значения суммы надо к предыдущему значению суммы прибавить значение модуля очередного слагаемого, умноженного на знак.
При расчете абсолютного значения дроби надо отметить закономерность:
· Числитель очередного слагаемого представляет собой стандартную функцию cos, аргументом которой является произведение порядкового номера члена суммы (обозначим его переменной k) на переменную х, то есть cos ( k * x ).
· Знаменатель очередной дроби можно представить в виде произведения двух сомножителей: квадрата выражения (2* k -1) и очередной степени переменной х (обозначим эту часть переменной st), которую можно получить путём умножения значения st предыдущей дроби на x. Зададим начальное значение st = 1.
В варианте а) число членов суммы заранее известно (равно N), и для решения задачи удобно использовать цикл с параметром.
В варианте б) значение очередного слагаемого следует запомнить в некоторой переменной (sl), чтобы использовать его при проверке условия прекращения вычислений – модуль последнего слагаемого должен быть меньше заданной величины e.
Вычисление суммы в варианте б) организуем с помощью цикла repeat: до тех пор пока очередное слагаемое по модулю не станет меньше e (в алгоритме обозначим её Е), будем выполнять действия в цикле. После завершения цикла искомая сумма будет вычислена.
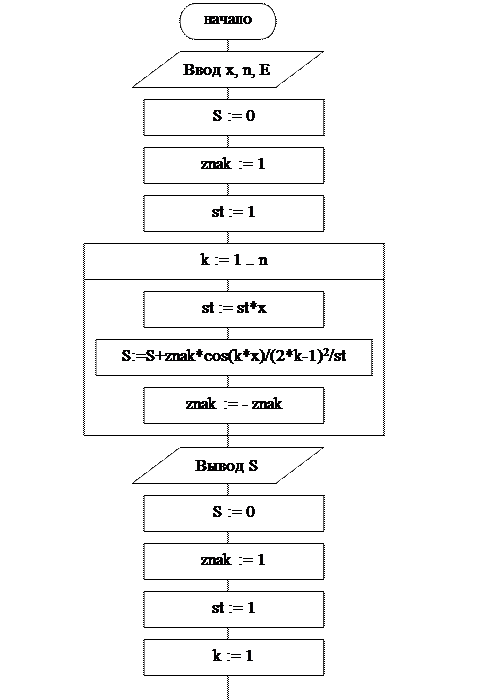
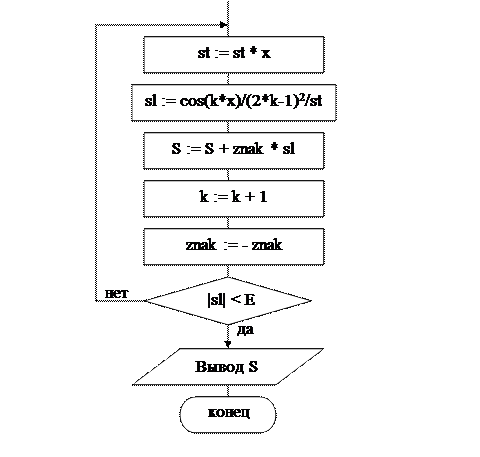
Блок-схема алгоритма
Данные для тестирования
1) Для x = 1, n = 3, Е = 0,04
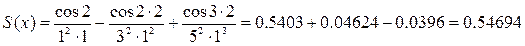
2) Для x = 2, n = 4, Е = 0,0005
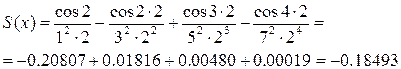
Для вычисления значений подобных выражений и подбора подходящих значений переменной х очень удобно пользоваться электронными таблицами Excel (рисунок 5.1).
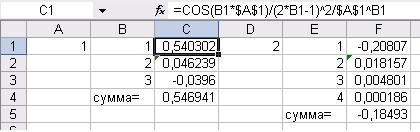
Рисунок 5.1 – Вычисление отдельных слагаемых и суммы в Microsoft Excel
Решение задачи
Выберем схему решения поставленной задачи.
После того как будут введены элементы массива, с помощью оператора цикла с параметром (for) и условного оператора организуем проверку номера элемента на нечетность и значения элемента на четность. Для этого можно воспользоваться стандартной функцией языка Паскаль odd(x), которая возвращает истину, если х – нечетно, и ложь, если х – четное.
Если обозначить i – номер очередного элемента массива, тогда заданное в задаче условие можно записать с помощью логического выражения:
odd(i) and (not odd(abs(A[i])))
Если результатом этого выражения будет истина, то к переменной K прибавляем 1 и такой элемент массива выводим на экран. По окончании цикла на экран выводим получившееся К.
Блок-схема алгоритма – представлена на рисунке 6.1.
Данные для тестирования
1) Для n = 10, A = {5, 7, 8, 10, -12, 3, 1, 4, 6, 2}
ð A[3] = 8
A[5] = -12
A[9] = 6
Пример 6.2 . Дан целочисленный массив {x} размера N и целое число a. Если в массиве {x} есть хотя бы один элемент, равный a, то получить сумму всех элементов, следующих за первым таким элементом. В противном случае вывести сообщение об отсутствии такого элемента.
Решение задачи
Выберем схему решения поставленной задачи. В этой задаче требуется:
1) определить имеется ли вообще в заданном массиве элемент, равный числу а;
2) если, такой элемент имеется, то запомнить его номер;
3) вычислить сумму элементов массива, предшествующих найденному элементу или вывести сообщение об отсутствии такового.
Чтобы запомнить номер искомого элемента, введём переменную K. Первоначально зададим K = 0.
После того как будут введены все элементы массива {x} и число а, с помощью оператора цикла с параметром (for) и условного оператора организуем поиск элемента, равного а. Как только будет найден первый такой элемент, присвоим его номер переменной K и, с помощью процедуры break, прервём дальнейшее выполнение цикла for, т.е. просмотр оставшейся части массива. Если мы проверим весь массив и элемента равного а не обнаружится, то значение переменной K останется равным нулю.
После завершения просмотра массива с помощью условного оператора проверим значение переменной K – если оно осталось равным нулю, то выведем сообщение об отсутствии элемента равного а, в противном случае с помощью оператора цикла for вычислим искомую сумму и выведем её значение.
Блок-схема алгоритма – представлена на рисунке 6.2.
Данные для тестирования
1) Для n = 10, x = {5, 7, 8, 10, -12, 3, 8, 1, 8, 2}, a = 8
ð S = 10-12+3+8+1+8+2 = 24
2) Для n = 10, x = {5, 7, 8, 10, -12, 3, 8, 1, 8, 2}, a = 4
ð В данном массиве нет элементов равных 4
Пример 6.3 . Дан целочисленный массив {ai} , i= 1,2, ..., n. Получить новый массив {bi}, выбросив из исходного массива все элементы со значением max({а i}). Определить число элементов нового массива.
Решение задачи
Выберем схему решения поставленной задачи.
После того как будут введены все элементы массива {a}, с помощью оператора цикла с параметром (for) и условного оператора организуем поиск максимального элемента. В методическом пособии [1] приведено решение задачи на нахождение минимального элемента массива. Поиск максимального элемента выполняется аналогично.
Введём переменную j – номер очередного элемента в новом массиве. Начальное значение j = 0. С помощью цикла с параметром и условного оператора «перепишем» в массив {bi} все элементы из массива {ai}, не равные максимальному.
Номер последнего элемента в массиве {bi} будет равен количеству элементов в новом массиве.
Блок-схема алгоритма – представлена на рисунке 6.3.
Данные для тестирования
1) Для n = 10, A = {10, 7, 8, 10, -1, 3, 8, 10, 8, 2}
ð Новый массив В: 7, 8, -1, 3, 8, 8, 2
В новом массиве 7 элементов
ВЛОЖЕННЫЕ ЦИКЛЫ
Если телом цикла является циклическая структура, то такие циклы называются вложенными. Возможно любое сочетание операторов цикла при организации вложенных циклов.
Приведём примеры решения задач с использованием вложенных циклов.
Пример 7.1 . Дано n натуральных чисел a1, a2, ... , an . Найти наибольший общий делитель.
Решение задачи
Выберем схему решения поставленной задачи.
Наибольшим общим делителем называется наибольшее число, на которое делятся все заданные числа, - в данном случае, таким числом может оказаться наименьший элемент данного массива {a}.
После того как будут введены все элементы массива {a}, с помощью оператора цикла с параметром (for) и условного оператора организуем поиск минимального элемента. Решение задачи на нахождение минимального элемента массива приведено в методическом пособии [1].
Затем, с помощью оператора цикла с параметром (for) будем перебирать в порядке убывания значения от min({a}) до 1. Во вложенном цикле на каждом шаге для всех элементов массива будем проверять кратность элемента очередному числу. Для осуществления такой проверки воспользуемся операцией mod (остаток от деления), а в качестве индикатора успешного результата введём логическую переменную t, первоначально на каждом шаге присваивая ей значение True (истина).
Если все элементы массива окажутся кратны очередному значению параметра внешнего цикла (значение переменной t останется True), то с помощью процедуры break выходим из цикла и выводим результат – значение параметра внешнего цикла на том шаге, на котором он был прерван.
Блок-схема алгоритма
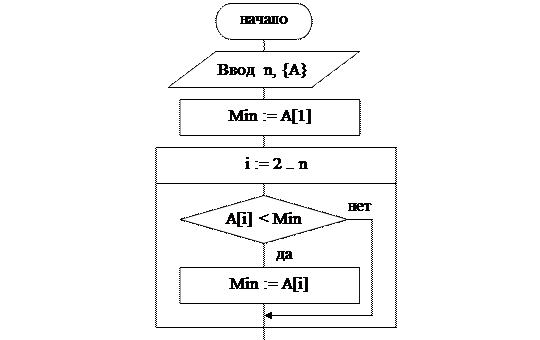
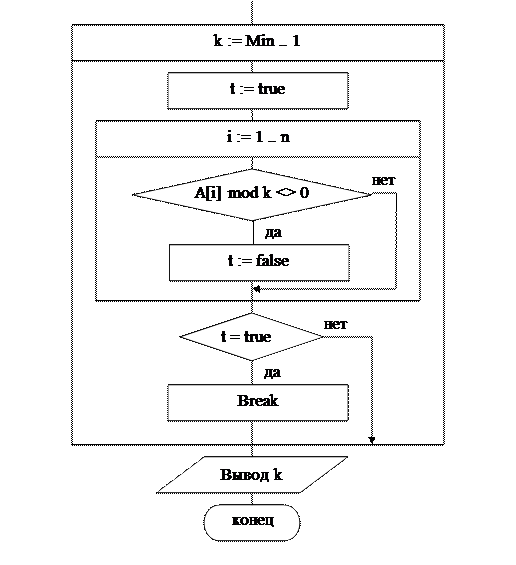
Данные для тестирования
1) Для n = 8, A = {15, 27, 18, 21, 12, 6, 51, 48}
ð Наибольший общий делитель равен 3
2) Для n = 5, A = {15, 75, 30, 45, 90}
ð Наибольший общий делитель равен 15
Пример 7.2 . Дан массив целых чисел {ai}, i = 1, 2, ... , n. Вывести те из них, которые встречаются в массиве по одному разу.
Решение задачи
Выберем схему решения поставленной задачи.
Ввод элементов массива {a} выполним обычным образом - с помощью оператора цикла с параметром (for).
Затем, с помощью оператора цикла с параметром (for) будем перебирать все элементы данного массива. Для каждого элемента введём переменную k с начальным значением k=0. Во вложенном цикле (также с помощью оператора цикла for) каждый элемент массива будем сравнивать со всеми элементами этого массива и, как только будет найден равный ему элемент, к переменной k будем прибавлять 1.
Если, после сравнения очередного элемента с элементами всего массива, значение переменной k будет равно 1, следовательно, он оказался равен только самому себе. Выводим этот элемент на экран.
Блок-схема алгоритма – приведена на рисунке 7.1.
Данные для тестирования
1) Для n = 10, A = {1, 2, 3, 4, 1, 3, 5, 4, 7, 3}
ð В данном массиве по одному разу встречаются
2 5 7
2) Для n = 10, A = {1, 5, 7, 5, 3, -1, 4, 5, 7, -3}
ð В данном массиве по одному разу встречаются
1 3 -1 4 -3
ПРОЦЕДУРЫ И ФУНКЦИИ
Подпрограммой называют обособленную, оформленную в виде отдельной синтаксической конструкции и снабжённую именем часть программы. Использование подпрограмм позволяет, сосредоточив в них подробное описание некоторых операций, в основной программе только указывать имена подпрограмм, чтобы выполнить эти операции. Такие вызовы подпрограммы возможны неоднократно из разных участков программы, причём при вызове подпрограмме можно передать некоторую информацию (различную в разных вызовах), чтобы одна и та же подпрограмма выполняла решение подзадачи для разных случаев.
Подпрограммы в Турбо Паскале реализованы посредством процедур и функций. Имея один и тот же смысл и аналогичную структуру, процедуры и функции различаются назначением и способом их использования.
Приведём примеры решения задач с использованием процедур и функций.
Пример 8.1 . Описать функцию SumDigit(K), находящую сумму цифр целого положительного числа K. Используя эту функцию, найти количество цифр для каждого из заданных целых положительных чисел {А i} i = 1, 2, ... , n.
Решение задачи
Выберем схему решения поставленной задачи.
В функции SumDigit(K) введём переменную S для накопления суммы цифр (начальное значение S=0). С помощью циклической структуры while и операций div и mod организуем выделение очередной цифры. Самую правую цифру числа можно получить, разделив нацело заданное число K на 10 и взяв остаток от деления. Результат целочисленного деления будем сохранять в этой же переменной K. Цикл будем выполнять пока переменная K будет больше нуля. Последним выполнимым оператором функции будет присвоение значения полученной суммы S имени функции.
В основной программе после того как будут введены все элементы массива {А}, с помощью оператора цикла с параметром (for) для каждого элемента массива организуем обращение к функции SumDigit, передавая в качестве параметра очередной элемент, и вывод результата.
Блок-схемы алгоритмов основной программы и функции SumDigit( K) – представлены на рисунке 8.1
Данные для тестирования
1) Для n = 3, A = {123, 4135, 47356}
ð Результат:
Сумма цифр числа 123 равна 1+2+3= 6
Сумма цифр числа 4135 равна 4+1+3+5= 13
Сумма цифр числа 47356 равна 4+7+3+5+6= 25
2) Для n = 4, A = {5753, 14, 5, 73}
ð Результат:
Сумма цифр числа 5753 равна 5+7+5+3= 20
Сумма цифр числа 14 равна 1+4= 5
Сумма цифр числа 5 равна 5
Сумма цифр числа 73 равна 7+3= 10
Пример 8.2 . Описать процедуру Massiv(Х, K, X _ c р, Т), находящую среднее арифметическое элементов массива {Х}, состоящего из K целых чисел, и возвращающую Т=True, если элементы массива упорядочены по неубыванию, и T=False в противном случае. Используя эту процедуру, вычислить среднее арифметическое и проверить упорядоченность элементов по неубыванию для двух целочисленных массивов {A} размером N и {B} размером М .
Решение задачи
Выберем схему решения поставленной задачи.
В процедуре Massiv(Х, K, X _ c р, Т) введём переменную S для накопления суммы элементов массива (начальное значение S=0). Вычисление суммы осуществляется с помощью оператора цикла с параметром (for) – на каждом шаге к переменной S добавляется очередной элемент массива. Среднее арифметическое элементов массива будет вычисляться: S / K.
Для определения упорядоченности элементов массива по неубыванию в процедуре введём переменную Т с начальным значением Т=True (предположим, массив упорядочен по неубыванию, т.е. x 1 ≤ x 2 ≤ x 3 ≤ .. ≤ xk). С помощью оператора цикла с параметром (for) для каждой пары элементов будем проверять нарушение условия упорядоченности, т.е. xi > xi +1. При выполнении такого условия переменной Т присваивается значение False.
В основной программе после того как будут введены все элементы массивов {А} и {В}, с помощью обращения к процедуре Massiv, вначале для массива {А}, а затем для массива {В} вычисляем нужные значения.
Поскольку массивы будут передаваться в процедуру в качестве параметров, то необходимо при описании массивов использовать описанный тип пользователя.
Блок-схемы алгоритмов основной программы и процедуры Massiv (Х,K, X _ c р ,Т ) – представлены на рисунке 8.2

Рисунок 8.2 – Блок-схемы алгоритма основной программы и функции для примера 8.2
Данные для тестирования
1) Для n = 8, A = {1, 2, 3, 4, 5, 6, 7, 8}
Для m = 5, B = {7, 2, 1, 4, 5}
ð Результат:
Среднее арифметическое элементов массива A равно 4.50
Массив A упорядочен по неубыванию
Среднее арифметическое элементов массива B равно 3.80
Массив B не упорядочен по неубыванию
Пример 8.3 . Для заданных действительного А и целого М вычислить значение выражения
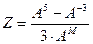
Возведение некоторого числа X в степень N организовать с помощью функции Stepen(Х, N).
Решение задачи
Выберем схему решения поставленной задачи.
Чтобы получить XN, нужно вычислить произведение 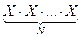 .
.
В функции Stepen(Х, N) введём переменную P для накопления произведения N сомножителей (начальное значение Р=1). Вычисление произведения осуществляется с помощью оператора цикла с параметром (for) – на каждом шаге переменная Р домножается на Х. Если N – отрицательное, то зададим Х = 1 / Х.
Последний выполнимый оператор в функции Stepen – присвоение результата имени функции, т.е. Stepen := Р.
В основной программе после того как будут введены значения А и M, с помощью обращения к функции Stepen с соответствующими аргументами, вычисляем значение выражения для Z.
Блок-схемы алгоритмов основной программы и функции Stepen (Х, N )

Данные для тестирования
1) Для A = 2, М = 3
ð Результат: Z = (25 – 2-3) / 3 / 23 = (32 – 0.125) / 24 = 1.328125
2) Для A = -2, М = -3
ð Результат: Z = ((-2)5 – (-2)-3) / 3 / (-2)-3 = (-32 + 0.125)*(-8) / 3 = 85
Работа с МАТРИЦами
В задачах этой темы исходная матрица (матрицы) должны считываться из заранее подготовленного текстового файла, в котором записана квадратная матрица размером не менее 6 строк и 6 столбцов. Числа, определяющие размер исходной матрицы (n или n, m) и другие скалярные исходные данные должны вводиться с клавиатуры.
После завершения работы программы исходная матрица и результаты работы программы должны быть выведены на экран и в текстовый файл.
Пример 9.1 . Дана матрица действительных чисел n ´ m, все элементы которой различны. Найти сумму элементов строки, в которой находится наименьший элемент матрицы и столбца, в котором находится наибольший элемент.
Решение задачи
Выберем схему решения поставленной задачи.
Прежде всего, на устройстве Е: создадим текстовый файл (назовём его data . txt), в котором разместим исходный массив размером не менее 6 строк и 6 столбцов. Это можно сделать с помощью приложения Блокнот или через редактор текста среды Turbo Pascal.
С помощью ввода с клавиатуры зададим размеры n и m исходной матрицы. Считывание элементов матрицы {А} из файла и вывод их на экран организуем с помощью вложенных операторов цикла с параметром (for).
Затем переходим к поиску наименьшего и наибольшего элементов массива. При отыскании наибольшего элемента будем запоминать номер столбца, в котором он находится, а при поиске наименьшего – номер его строки. Введём переменные:
min – значение наименьшего элемента массива;
max – значение наибольшего элемента массива;
k – номер столбца, в котором находится наибольший элемент массива;
r – номер строки, в котором находится наименьший элемент массива;
S – искомая сумма.
Вычисление искомой суммы элементов организуем также с использованием операторов цикла с параметром (for).
Блок-схема алгоритма


Данные для тестирования
Пусть в файле E:\data.txt хранятся следующие данные:
-11 2 13 4 15 6
7 -30 8 -1 9 12
11 -3 0 -2 50 -5
-9 16 20 5 -7 -20
17 -4 21 -6 22 -8
-7 18 -2 -15 1 -9
1) Для N = 4, M = 6
ð Исходная матрица:
-11.00 2.00 13.00 4.00 15.00 6.00
7.00 -30.00 8.00 -1.00 9.00 12.00
11.00 -3.00 0.00 -2.00 50. 00 -5.00
-9.00 16.00 20.00 5.00 -7.00 -20.00
Искомая сумма S = 7 – 30 + 8 – 1 + 9 + 12 + 15 + 9 + 50 – 7 = 72
2) Для N = 5, M = 4
ð Исходная матрица:
-11.00 2.00 13.00 4.00
7.00 -30.00 8.00 -1.00
11.00 -3.00 0.00 -2.00
-9.00 16.00 20.00 5.00
17.00 -4.00 21.00 -6.00
Искомая сумма S = 7 – 30 + 8 – 1 + 13 + 8 + 0 + 20 + 21 = 46
Пример 9.2 . Дана матрица действительных чисел n ´ m. Определить количество таких элементов матрицы, сумма индексов которых нечетна, и которые меньше суммы остальных элементов своего столбца.
Решение задачи
Выберем схему решения поставленной задачи.
Прежде всего, как и в предыдущей задаче, на устройстве Е: создадим текстовый файл (назовём его data . txt), в котором разместим исходный массив размером не менее 6 строк и 6 столбцов.
С помощью ввода с клавиатуры зададим размеры n и m исходной матрицы. Считывание элементов матрицы {А} из файла и вывод их на экран организуем с помощью вложенных операторов цикла с параметром (for).
Введём переменную k – количество элементов, удовлетворяющих заданному условию. Первоначально k = 0.
Для поиска указанных элементов и сравнения их с суммой остальных элементов соответствующего столбца будем использовать вложенные циклы с параметром. В качестве параметра во внешнем цикле введём переменную j, отвечающую за изменение номера столбца. В первом внутреннем цикле с параметром i (переменная i отвечает за изменение номера строки) для каждого столбца вычислим сумму всех его элементов. Для этого введём переменную S и для каждого столбца первоначально будем задавать S = 0.
Затем, во втором внутреннем цикле с параметром i с помощью условного оператора организуем проверку выполнения одновременно двух условий: 1) сумма индексов элемента Ai,j – нечётна (для этого можно воспользоваться, например, стандартной функцией odd(x)) и 2) элемент Ai,j меньше суммы остальных элементов своего столбца, т.е. меньше чем S - Ai,j. Если оба эти условия выполняются, то значение переменной k увеличиваем на 1.
Результатом решения задачи будет значение переменной k. Его необходимо вывести на экран и в текстовый файл (предположим, Е:\ result . txt).
Блок-схема алгоритма


Данные для тестирования
Пусть в файле E:\data.txt хранятся следующие данные:
-11 2 13 4 15 6
7 -30 8 -1 9 12
11 -3 0 -2 50 -5
-9 16 20 5 -7 -20
17 -4 21 -6 22 -8
-7 18 -2 -15 1 -9
1) Для N = 4, M = 6
ð Исходная матрица:
-11.00 2.00 13.00 4.00 15. 00 6.00
7.00 -30.00 8.00 -1.00 9.00 12.00
11.00 -3.00 0.00 -2.00 50.00 -5.00
-9.00 16.00 20.00 5.00 -7.00 -20.00
В заданной матрице искомых элементов k = 8
Список литературы
Основная литература
1 Епанишников А., Епанишников В. Программирование в среде Turbo Pascal 7.0. - М.: “ДИАЛОГ-МИФИ”, 1993.-288с.
2 Культин Н.Б. Программирование в Turbo Pascal 7.0 и Delphi –СПб: БХВ-Петербург, 2000.-416 с.: ил
3 Культин Н.Б. Turbo Pascal в задачах и примерах –СПб: БХВ-Петербург, 2000.-256 с.: ил.
4 Турбо Паскаль 7.0 - К.: Торгово-издательское бюро BHV, 1996.-480 с.: ил.
5 Фаронов В.В. Турбо Паскаль. В 3 кн. Кн.1. - М.: Учебно-инженерный центр "МВТУ-ФЕСТО ДИДАКТИК",1992.-304 с.: ил.
Дополнительная литература
1 Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И.. Задачи по программированию - М.: Наука, 1988. - 224 с.
2 Вьюкова Н.И., Галатенко В.А., Ходулев А.Б. Систематический подход к программированию/ под ред. Ю.М. Баяковского.-М.: Наука, 1993.-208с.
3 Гловацкая А.П. Методы и алгоритмы вычислительной математики. Учеб. пособие. –М.: Радио и связь, 1999.- 408 с.
4 Докукина Т.К. Программирование и алгоритмические языки. - М.: Машиностроение, 1993. - 496 с.:ил
5 Зуев Е.А. Язык программирования Turbo Pascal 6.0, 7.0/ - М.: Веста, Радио и связь, 1993. -384с.:ил.
6 Пильщиков В.Н. Сборник упражнений по языку Паскаль: Учеб. пособие для вузов. - Наука. 1989. - 160 с.
7 Прайс Д. Программирование на языке Паскаль. Пер. с англ. - М.: Мир, 1987. - 232 с.
8 Программное обеспечение микроЭВМ. В 11 кн. Кн. 7. Программирование на языке Паскаль. /Шаньгин В.Ф., Поддубная Л.М., Голубев-Новожилов Ю.С.; Под ред. В.Ф. Шаньгина.- М.: Высшая школа, 1988. - 125 с.
9 Фаронов В.В. Турбо Паскаль. В 3 кн. Кн.3. Практика программирования. Часть 1. - М.: Учебно-инженерный центр "МВТУ-ФЕСТО ДИДАКТИК",1993.-256 с.: ил.
10 Фаронов В.В. Турбо Паскаль. В 3 кн. Кн.3. Практика прграммирования . Часть 2. - М.: Учебно-инженерный центр "МВТУ-ФЕСТО ДИДАКТИК",1993.-304 с.: ил.
11 Форсайт Р. Паскаль для всех. Пер. с англ. - М.: Машиностроение,1986. - 288 с.: ил.
12 Электронные вычислительные машины: в 8-ми кн.: Учебное пособие для вузов. Кн.5. Алексеев В.Е., Ваулин Л.С. Языки программирования. - М. Высшая школа, 1987. - 143 с.: ил.
Методические пособия
1 Николаев Н. А. Основы программирования в системе Turbo Pascal 7.0. Учебно-методическое пособие по курсам:«Информатика», «Программирование и алгоритмизация».- Новоуральск, НПИ, 2000, -69 с..
2 Николаев Н. А. Работа с графикой в системе Turbo Pascal. Методическое пособие по курсу «Программирование на языках высокого уровня» для студентов специальности 230102 дневной формы обучения. Новоуральск, НГТИ, 2006, -48 с
3 Николаев Н.А. Сборник заданий по программированию. Часть 1. - Методическое пособие по курсам: "Программирование на языке высокого уровня", "Программирование и основы алгоритмизация", "Информатика" для студентов всех специальностей очной и очно-заочной форм обучения., Новоуральск, НГТИ, 2007, 52 с.
4 Орлова И. В. Основы работы в интегрированной среде Турбо Паскаль 7.0. Учебно-методическое пособие по курсу «Информатика» для всех специальностей. Новоуральск, НПИ, 2001, -43 с.
УДК 681.3.06
Автор: Орлова Ирина Викторовна
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ПРОГРАММИРОВАНИЮ.
Часть 1.
Учебно-методическое пособие по курсам «Информатика»,
«Программирование и основы алгоритмизации»,
«Программирование на языках высокого уровня»
для студентов всех специальностей очной формы обучения
Новоуральск, НТИ НИЯУ МИФИ, 2010, 56 с.
Новоуральский технологический институт
Кафедра информатики и программирования
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПО ПРОГРАММИРОВАНИЮ
Часть 1
Учебно-методическое пособие по курсам
«Информатика», «Программирование и основы алгоритмизации»,
«Программирование на языках высокого уровня»
для студентов всех специальностей
очной формы обучения
Новоуральск 2010
УДК 681.3.06
МиМ – 2.3. - - 10
Автор Орлова Ирина Викторовна
Рецензент кандидат физико-математических наук, доцент кафедры ВМ Фоминых Марина Анатольевна
Примеры решения задач по программированию. Часть 1. Учебно-методическое пособие по курсам «Информатика», «Программирование и основы алгоритмизации», «Программирование на языках высокого уровня» для студентов всех специальностей очной формы обучения
Новоуральск, НТИ НИЯУ МИФИ, 2010, 56 с.
Пособие представляет собой описание решения 21 задачи по программированию на языке Паскаль по основным девяти темам, изучаемым в курсах «Информатика», «Программирование и основы алгоритмизация» и «Программирование на языках высокого уровня» в НТИ НИЯУ МИФИ.
Содержит 21 библиографических названия.
Пособие может использоваться при самостоятельном изучении программирования на языке Паскаль».
Методическое пособие рассмотрено на заседании кафедры
Протокол № 117 от 21 июня 2010 г.
Зав.кафедрой Н.А.Николаев
СОГЛАСОВАНО:
Председатель методкомиссии НТИ НИЯУ МИФИ
д.т.н., профессор А.Е.Беляев
Оглавление
ВВедение.. 4
1 ОПЕРАТОР ПРИСВАИВАНИЯ.. 5
2 УСЛОВНЫЙ ОПЕРАТОР.. 8
3 ПРОСТЕЙШИЕ ЦИКЛЫ... 13
4 ЧИСЛОВЫЕ РЯДЫ... 19
5 ФУНКЦИОНАЛЬНЫЕ РЯДЫ... 25
6 ЗАДАЧИ С ИСПОЛЬЗОВАНИЕМ МАССИВОВ.. 29
7 ВЛОЖЕННЫЕ ЦИКЛЫ... 35
8 ПРОЦЕДУРЫ И ФУНКЦИИ.. 40
9 работа с МАТРИЦами.. 47
Список литературы... 54
ВВедение
Студенты НТИ НИЯУ МИФИ различных специальностей изучают программирование в курсах "Программирование на языке высокого уровня", "Программирование и основы алгоритмизации" и "Информатика" в разных объёмах, но в любом случае основой изучения данной темы является лабораторный практикум, который структурно делится на две части: общий практикум, сопровождающий основной курс по программированию, и практикум по численным методам, нацеленный на приобретение студентами опыта решения на ЭВМ определенных классов задач, а также на практическое освоение студентами специализированных компонент математического обеспечения.
Каждая задача практикума – это самостоятельная задача с краткой, но четкой содержательной формулировкой, не содержащей описания алгоритма. В процессе решения задачи от студента требуется:
- составить алгоритм решения задачи;
- записать алгоритм в виде программы на Паскале;
- произвести отладку программы;
- протестировать программу по заранее подготовленным данным;
Первый и второй этапы выполняются дома при подготовке к лабораторной работе, третий и четвертый - во время лабораторной работы.
Студентам, только начинающим изучать основы алгоритмизации и программирование, а также имеющим не достаточно глубокие знания элементарной математики, математического анализа и линейной алгебры, бывает трудно представить ход решения предлагаемых задач и правильно оформить отчёт к лабораторной работе по программированию.
В данном пособии рассматриваются примеры решения задач по первой, общей части практикума. Представленные в пособии задачи сгруппированы по девяти темам, которые соответствуют темам лабораторных работ, задания для которых содержатся в методическом пособии [3] и практически полностью охватывают материал, изучаемый студентами всех специальностей в первом семестре изучения соответствующего курса.
На каждую тему в данном пособии приводится по 2–3 примера, которые подобраны так, чтобы рассмотреть наиболее часто используемые приёмы при решении задач указанной темы. Для каждой из рассматриваемых задач, помимо условия, приводится математическая модель или описание рассуждений, используемых при решении задачи, затем приводится блок-схема алгоритма, текст программы на языке Паскаль и данные для тестирования, с помощью которых можно проверить правильность работы представленной программы.
Настоящее пособие может быть использовано студентами при подготовке к лабораторным и контрольным работам или изучающими самостоятельно тему «Основы алгоритмизации и программирования на языке Паскаль», преподавателями при подготовке и проведении лекций по этой теме в курсах «Информатика», «Программирование и основы алгоритмизации» и «Программирование на языках высокого уровня», а также сотрудниками, которые в своей работе встречаются с необходимостью составления алгоритмов и написания программ на языке Паскаль.
ОПЕРАТОР ПРИСВАИВАНИЯ
В этом разделе рассматриваются примеры решения простейших задач, алгоритм которых имеет линейную структуру. По каждой задаче составлена программа, содержащая операторы ввода исходных данных, присваивания и вывода результатов. В программах предусмотрен вывод подсказки для ввода и пояснения результата при выводе.
Пример 1.1. Дано натуральное трехзначное число. Вычислить сумму его цифр.
Дата: 2019-03-05, просмотров: 342.