i=[1 2 3 4 5] - создает вектор-строку из пяти элементов.
i=[1;2;3;4;5] - создает вектор-строку из пяти элементов.
i=1:0.5:20 - создает вектор-строку из равноотстоящих на величину 0.5 элементов в диапазоне от 1 до 20.
i=(1:0.5:20)’ - создает вектор-строку из равноотстоящих на величину 0.5 элементов в диапазоне от 1 до 20.
Символ «’» обозначает эрмитово сопряжение – сочетание транспонирования и комплексного сопряжения. Так как элементы вектора вещественные, комплексное сопряжение ничего не меняет.
Для указания транспонирования без комплексного сопряжения необходимо добавить точку – «.’».
Команда L=length(x) возвращает длину вектора х.
Точка используется и для указания поэлементных операций умножения и деления матриц.
Y=A*B - умножение матриц A и B по правилам матричной алгебры.
Y=A.*B - перемножает одноименные элементы матриц А и В.
Самый простой способ формирования матриц заключается в непосредственном вводе их элементов (по строкам) с клавиатуры – например: А= [1 2 3; 4 5 6; 7 8 9], получается матрица А размером 3*3:
А= 1 2 3
4 5 6
7 8 9.
Следующие матричные функции обеспечивают генерацию некоторых наиболее распространенных видов матриц размерностью M на N:
Zeros(M,N) – генерация матрицы с нулевыми элементами,
Ones(M,N) – генерация матрицы с единичными элементами,
Rand(M,N) – генерация матрицы с элементами, имеющими случайные значения,
Eye(M,N) – генерация матрицы с единичными диагональными элементами.
Операции с многочленами и матрицами.
Система MatLab имеет функцию roots (P), возвращающую вектор, коэффициенты которого являются корнями заданного многочлена Р.
Многочлен задается в виде вектора коэффициентов при переменной, начиная со старшего – например: S( x)= x5+8 x4-31 x3+80 x2+94 x-20 в MatLab будет записан:
>> S=[1 8 -31 80 94 -20]
S =
1 8 -31 80 94 -20
>> roots(S) – решение заданного многочлена:
ans =
-11.3026
2.0475 + 2.3585i
2.0475 - 2.3585i
-0.9779
0.1855 ,
где ans—название результирующей переменной по умолчанию.
Операции с матрицами можно выполнять по правилам вычисления матриц, а так же выполнять действия по элементно – сравните:
>> A=[1 2 3;4 5 6;1 1 1];
>> B=[1 2 1; 3 3 3; 3 2 1];
>> C=A*B
C =
16 14 10
37 35 25
7 7 5
>> D=A.*B
D =
1 4 3
12 15 18
3 2 1.
Работа с графическими средствами.
Основные операторы графики:
Plot – построение графика в линейном масштабе,
Polar – построение графика в полярной системе координат,
Mesh – построение графика трехмерной поверхности,
Plot3 – построение графика трехмерной поверхности,
Surf– построение графика трехмерной поверхности,
Text – вывод надписи в заданное место графика,
title – задание титульной надписи,
xlabel – задание надписи по х,
ylabel – задание надписи по у,
grid – задание пунктирной масштабной сетки,
Clg – очистка графического экрана,
Hold – сохранение предшествующих построений,
Shg – показ графического экрана,
pause – задание паузы в вычислениях.
Если необходимо построить несколько графиков на одной картинке, то необходимо вставить команду «hold on». Все последующие графики будут накладываться на одну сетку. Отмена данной команды происходит повторным набором. Чтобы графики были различны, их можно рисовать разными линиями и разным цветом:
| Тип линий | Тип точек | Цвета |
| Черта - | Плюс + | Красный r |
| Пунктир -- | Звёздочка * | Зелёный G |
| Двоеточие : | Кружок о | Синий B |
| Штрих-пунктир -. | Крестик х | Белый W |
Примеры.
1. Построить графики затухающих колебаний: x( t)= e-0.2 t sin( t), y( t)= e-0.2 t cos( t), где t изменяется от 0 до 10 с шагом 0,1. Выполнение этого задания должно выглядеть следующим образом:
t=0:.1:10;
x=exp(-.2*t)*sin(t);
y= exp(-.2*t)*cos(t);
Plot(t,x,t,y), grid.
2. Построить графики полярного уравнения логарифмической спирали r=e-0.2t и добавить к ней единичную окружность. Выполнение этого задания должно выглядеть следующим образом:
t=0:.1:10;
r=exp(-.2*t)
Polar(t,r),grid.
Затем необходимо добавить:
hold on;
Polar(t, ones(t)).
3. Построить график трехмерной поверхности 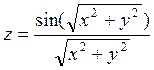 .
.
Выполнение этого задания должно выглядеть следующим образом:
>> [x,y]=meshgrid(-15:0.5:15);
>> R=sqrt(x.^2+y.^2)+eps;
>> z=sin (R)./R;
>> plot3(x,y,z),grid
Что бы график выглядел более гладким можно выбрать surf(x,y,z). если необходимо стереть грани и сделать график гладким необходимо набрать следующие команды:
>> surf(x,y,z);
>> shading interp.
Дата: 2019-03-05, просмотров: 273.