Ядро пакета MatLab образуют встроенные функции, входящие в раздел BIN (Built IN functions). MatLab содержит справочник HELP по встроенным функциям

Стр 1 из 2Следующая ⇒

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Ядро пакета MatLab образуют встроенные функции, входящие в раздел BIN (Built IN functions). MatLab содержит справочник HELP по встроенным функциям.

Задание 1.

1. Построить вектор-строку с параметрами – от минус последняя цифра № студенческого до плюс последняя цифра № студенческого с шагом – 0,2 (Например: № студенческого 04/5050 – получаемый интервал – от –10 до +10).

2. Определить длину вектора.

3. Преобразовать вектор-строку в вектор-столбец.

Задание 2.

1. Создайте матрицу 4*4: строка простых чисел; строка месяц и день рождения; строка год рождения; строка № студенческого. Строки можно располагать в любом порядке (Пример: Дата рождения – 5 марта 1987года, № студенческого – 04/5050. получаемая матрица:

1 9 8 7 – год рождения

3 5 17 23 – простые числа

5 0 5 0 – № студенческого

0 5 0 3 – день и месяц рождения).

2. Создайте матрицу, транспонированную от исходной, и с уменьшенным каждым элементом на 7.

(Транспонирование меняет строки и столбцы.)

3. Перемножьте данные матрицы по правилам вычисления матриц и поэлементно. Сравните полученные результаты.

Задание 3 .

1. Построить на одной сетке графики экспоненциальных функций с различными коэффициентами.

y=А*exp(-В*i), А,В — произвольные константы.

2. Построить на новой сетке графики затухающих гармонических колебаний с различными коэффициентами.

Y =А* exp (-В* i ).* cos (2* pi * i + Fi ), А,В, Fi — произвольные константы.

3. В полярной системе координат построить свёртывающуюся спираль с различными коэффициентами (Общий вид уравнения аналогичен предыдущему заданию).

4. Создать сложные (используя sin, cos, tg, log, …) вспомогательные функции, и построить в 3-х мерной поверхности график взаимодействия этих функций (интервал переменной можно задать от –10 до 10 с шагом 0,2).

Литература.

1. Ануфриев И. MatLab 5.3/6.х – самоучитель, «ВВХВ-Петербург»,С-Пб 2003г. 722стр.;

2. Дьяконов В.П. Справочник по применению системы MatLab – М., 1993г.. 112стр.

3. Всемирнова Е. Информатика. Учебное пособие.-:СПб, ГУАП

Приложение.

Некоторые справочные сведения по применению системы MatLab

Формирование векторов и матриц.

i=[1 2 3 4 5] - создает вектор-строку из пяти элементов.

i=[1;2;3;4;5] - создает вектор-строку из пяти элементов.

i=1:0.5:20 - создает вектор-строку из равноотстоящих на величину 0.5 элементов в диапазоне от 1 до 20.

i=(1:0.5:20)’ - создает вектор-строку из равноотстоящих на величину 0.5 элементов в диапазоне от 1 до 20.

Символ «’» обозначает эрмитово сопряжение – сочетание транспонирования и комплексного сопряжения. Так как элементы вектора вещественные, комплексное сопряжение ничего не меняет.

Для указания транспонирования без комплексного сопряжения необходимо добавить точку – «.’».

Команда L=length(x) возвращает длину вектора х.

Точка используется и для указания поэлементных операций умножения и деления матриц.

Y=A*B - умножение матриц A и B по правилам матричной алгебры.

Y=A.*B - перемножает одноименные элементы матриц А и В.

Самый простой способ формирования матриц заключается в непосредственном вводе их элементов (по строкам) с клавиатуры – например: А= [1 2 3; 4 5 6; 7 8 9], получается матрица А размером 3*3:

А= 1 2 3

4 5 6

7 8 9.

Следующие матричные функции обеспечивают генерацию некоторых наиболее распространенных видов матриц размерностью M на N:

Zeros(M,N) – генерация матрицы с нулевыми элементами,

Ones(M,N) – генерация матрицы с единичными элементами,

Rand(M,N) – генерация матрицы с элементами, имеющими случайные значения,

Eye(M,N) – генерация матрицы с единичными диагональными элементами.

Операции с многочленами и матрицами.

Система MatLab имеет функцию roots (P), возвращающую вектор, коэффициенты которого являются корнями заданного многочлена Р.

Многочлен задается в виде вектора коэффициентов при переменной, начиная со старшего – например: S( x)= x⁵+8 x⁴-31 x³+80 x²+94 x-20 в MatLab будет записан:

>> S=[1 8 -31 80 94 -20]

S =

1 8 -31 80 94 -20

>> roots(S) – решение заданного многочлена:

ans =

-11.3026

2.0475 + 2.3585i

2.0475 - 2.3585i

-0.9779

0.1855 ,

где ans—название результирующей переменной по умолчанию.

Операции с матрицами можно выполнять по правилам вычисления матриц, а так же выполнять действия по элементно – сравните:

>> A=[1 2 3;4 5 6;1 1 1];

>> B=[1 2 1; 3 3 3; 3 2 1];

>> C=A*B

C =

16 14 10

37 35 25

7 7 5

>> D=A.*B

D =

1 4 3

12 15 18

3 2 1.

Примеры.

1. Построить графики затухающих колебаний: x( t)= e^-0.2 ^t sin( t), y( t)= e^-0.2 ^t cos( t), где t изменяется от 0 до 10 с шагом 0,1. Выполнение этого задания должно выглядеть следующим образом:

t=0:.1:10;

x=exp(-.2*t)*sin(t);

y= exp(-.2*t)*cos(t);

Plot(t,x,t,y), grid.

2. Построить графики полярного уравнения логарифмической спирали r=e^-0.2^t и добавить к ней единичную окружность. Выполнение этого задания должно выглядеть следующим образом:

t=0:.1:10;

r=exp(-.2*t)

Polar(t,r),grid.

Затем необходимо добавить:

hold on;

Polar(t, ones(t)).

3. Построить график трехмерной поверхности .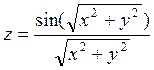

Выполнение этого задания должно выглядеть следующим образом:

>> [x,y]=meshgrid(-15:0.5:15);

>> R=sqrt(x.^2+y.^2)+eps;

>> z=sin (R)./R;

>> plot3(x,y,z),grid

Что бы график выглядел более гладким можно выбрать surf(x,y,z). если необходимо стереть грани и сделать график гладким необходимо набрать следующие команды:

>> surf(x,y,z);

>> shading interp.