КОНТРОЛЬНАЯ РАБОТА № 2
Студент решает 6 задач своего варианта, номер которого совпадает с последней цифрой шифра. Номера задач каждого варианта представлены в табл. 9.
5.1. Таблица вариантов контрольной работы № 2
| Вариант | Номера задач | |||||
| 0 | 210 | 220 | 230 | 240 | 250 | 260 |
| 1 | 201 | 211 | 221 | 231 | 241 | 251 |
| 2 | 202 | 212 | 222 | 232 | 242 | 252 |
| 3 | 203 | 213 | 223 | 233 | 243 | 253 |
| 4 | 204 | 214 | 224 | 234 | 244 | 254 |
| 5 | 205 | 215 | 225 | 235 | 245 | 255 |
| 6 | 206 | 216 | 226 | 236 | 246 | 256 |
| 7 | 207 | 217 | 227 | 237 | 247 | 257 |
| 8 | 208 | 218 | 228 | 238 | 248 | 258 |
| 9 | 209 | 219 | 229 | 239 | 249 | 259 |
Таблица 9
Рекомендации к решению задач по разделу «Электромагнетизм»
1. Внимательно прочитайте условие задачи. Выясните, какое явление рассматривается в задаче, и изучите сведения о нем и о физических величинах, его описывающих, по учебному пособию.
2. При определении магнитных сил, магнитного потока и других величин обратите внимание на то, какое магнитное поле рассматривается в задаче – однородное или неоднородное. В первом случае используйте более простые формулы для однородного МП.
3. При решении задачи определяйте направления искомых векторов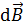 
, 
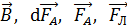и др. Для этого используйте а) определительные формулы, в правой части которых записано векторное произведение векторов или б) правило буравчика и правило левой руки.
4. В том случае, если магнитное поле создается в ферромагнетике, для которого магнитная проницаемость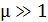 
(в отличие от картонного или воздушного сердечника, имеющего 
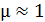), необходимо определять величину 
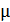по формуле, связывающей напряженность 
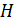и магнитную индукцию 
:
.
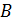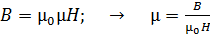При этом следует учесть, что величина магнитной индукции зависит от напряженности МП: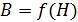 
, – и соответственно 
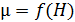. Поэтому сначала вычисляют напряженность магнитного поля 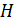, которая зависит только от тока в контуре и формы и размеров контура (катушки). Затем по экспериментальному графику кривой намагничивания 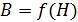для заданного материала сердечника (используя справочные данные) по рассчитанной величине 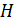определяют индукцию магнитного поля 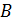. По найденным значениям 
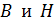вычисляют магнитную проницаемость сердечника по записанной выше формуле.
ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ № 2
Сила Лоренца. Движение заряженных частиц
Магнитный поток. Работа по перемещению проводника с током
В магнитном поле
221. Плоский контур площадью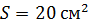 
находится в однородном магнитном поле с индукцией 
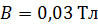. Определите магнитный поток 
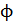, пронизывающий контур, если его плоскость составляет угол 
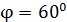с направлением линий магнитной индукции.
222. Магнитный поток сквозь сечение соленоида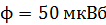 
. Длина соленоида 
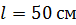. Определите магнитный момент 
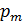соленоида, если его витки плотно прилегают друг к другу.
223. В средней части соленоида, содержащего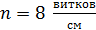 
, помещен круговой виток диаметром 
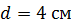. Плоскость витка расположена под углом 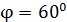к оси соленоида. Определите магнитный поток 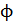, пронизывающий виток, если по обмотке соленоида течет ток 
.
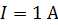224. На длинный цилиндрический каркас радиусом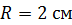 
уложена «виток к витку» однослойная обмотка из проволоки диаметром 
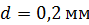. Определите магнитный поток 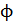, создаваемый таким соленоидом при силе тока 
.
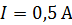225. Плоский контур с током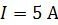 
свободно установился в однородном магнитном поле с индукцией 
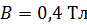. Площадь контура 
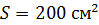. Поддерживая ток в контуре неизменным, его повернули относительно оси, лежащей в плоскости контура, на угол 
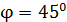. Определите совершенную при этом работу 
.
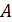226. Квадратный контур со стороной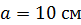 
, в котором течет ток 
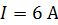, находится в магнитном поле с индукцией 
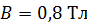; плоскость контура расположена под углом 
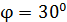к линиям магнитной индукции. Какую работу 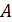нужно совершить, чтобы при неизменной силе тока в контуре изменить его форму на окружность?
227. Виток, в котором поддерживается постоянная сила тока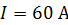 
, свободно установился в однородном магнитном поле с индукцией 
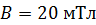. Радиус витка 
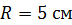. Какую работу 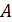нужно совершить для того, чтобы повернуть виток относительно оси, совпадающей с его диаметром, на угол .
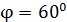228. В однородном магнитном поле перпендикулярно линиям индукции расположен плоский контур площадью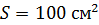 
. Поддерживая в контуре постоянную силу тока 
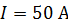, его переместили в область пространства, где поле отсутствует. Определите магнитную индукцию поля 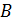, если при перемещении контура была совершена работа 
.
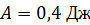229. Плоский круговой контур радиусом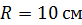 
с током 
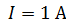расположен в однородном магнитном поле с индукцией 
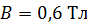так, что нормаль к контуру перпендикулярна линиям магнитной индукции. Определите работу 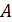, совершаемую силами поля при медленном повороте контура вокруг оси, лежащей в плоскости контура, на угол 
.
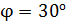230. Определите магнитный поток 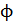, пронизывающий соленоид, если его длина 
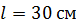и магнитный момент 
.
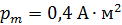Энергия магнитного поля
231. В однородном магнитном поле с индукцией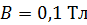 
равномерно с частотой 
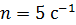вращается проводящий стержень длиной 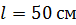так, что плоскость его вращения перпендикулярна линиям магнитной индукции, а ось вращения проходит через конец стержня. Определите разность потенциалов 
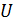, индуцируемую на концах стержня.
232. В однородном магнитном поле с индукцией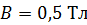 
вращается с частотой 
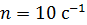проводящий стержень длиной 
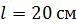. Плоскость его вращения перпендикулярна линиям магнитной индукции, а ось вращения проходит через конец стержня. Определите разность потенциалов 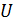, индуцируемую на концах стержня.
233. В проволочное кольцо, присоединенное к интегратору тока, вставили прямой магнит. При этом по цепи прошел заряд 
. Покажите на схеме цепи направление индукционного тока в кольце и определите изменение магнитного потока 
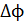через плоскость кольца, если сопротивление цепи 
.
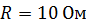234. Замкнутый медный провод массой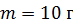 
, имеющий форму квадрата, помещен в однородное магнитное поле с индукцией 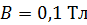так, что плоскость контура перпендикулярна линиям поля. Покажите на схеме направление индукционного тока в контуре и определите заряд 
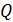, который потечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию.
235. Рамка из провода сопротивлением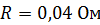 
равномерно вращается в однородном магнитном поле с индукцией 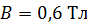. Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Площадь рамки 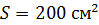. Покажите направление индукционного тока в рамке и определите заряд 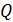, который потечет по рамке при изменении угла между нормалью к рамке и линиями индукции от 0 до 
.
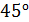236. Проволочный виток диаметром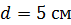 
и сопротивлением 
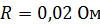находится в однородном магнитном поле с индукцией 
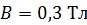. Плоскость витка составляет угол 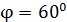с линиями индукции. Какой заряд 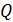протечет по витку при выключении магнитного поля? Покажите направление индукционного тока в витке.
237. Рамка, содержащая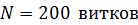 
тонкого провода, может свободно вращаться вокруг оси, лежащей в плоскости рамки. Площадь рамки 
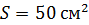. Ось вращения рамки перпендикулярна линиям однородного магнитного поля с индукцией 
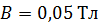. Определите максимальную ЭДС 
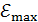, которая индуцируется в рамке при ее вращении с частотой 
.
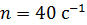238. Прямой проводящий стержень длиной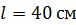 
находится в однородном магнитном поле с индукцией 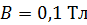. Концы стержня замкнуты проводом, находящимся вне поля. Сопротивление цепи 
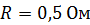. Какая мощность 
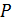требуется для равномерного движения стержня со скоростью 
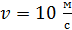, перпендикулярной линиям магнитной индукции?
239. Проволочный контур площадью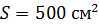 
и сопротивлением 
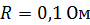равномерно вращается в однородном магнитном поле с индукцией 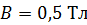. Ось вращения лежит в плоскости контура и перпендикулярна линиям магнитной индукции. Определите максимальную мощность 
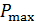, необходимую для вращения контура с угловой скоростью 
.
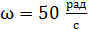240. Кольцо из медного провода массой 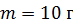помещено в однородное магнитное поле с индукцией 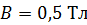; плоскость кольца составляет угол 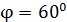с линиями магнитной индукции. Покажите направление индукционного тока и определите заряд 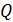, который пройдет по кольцу, если снять магнитное поле.
241. Соленоид сечением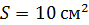 
содержит 
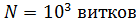. При силе тока 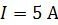магнитная индукция поля внутри соленоида 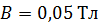. Определите индуктивность 
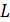соленоида и энергию его магнитного поля 
.
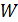242. На картонный каркас радиусом 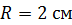и длиной 
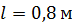намотан в один слой провод диаметром 
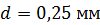так, что витки плотно прилегают друг к другу. Вычислите индуктивность 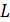полученного соленоида.
243. Катушка, намотанная на цилиндрический каркас, имеет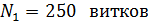 
и индуктивность 
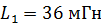. Чтобы увеличить индуктивность катушки до 
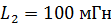, обмотку катушки заменили обмоткой из более тонкого провода с таким расчетом, чтобы длина катушки 
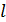осталась прежней. Какое число витков 
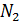оказалось в катушке после перемотки?
244. Индуктивность соленоида с однослойной обмоткой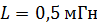 
. Длина соленоида 
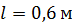, радиус 
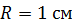. Определите отношение числа витков соленоида к его длине: 
.
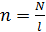245. Обмотка соленоида содержит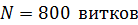 
. Сердечник из немагнитного материала имеет сечение 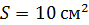. По обмотке течет ток, создающий поле с магнитной индукцией 
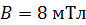. Определите среднее значение ЭДС самоиндукции 
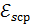, которая появится на зажимах соленоида, если сила тока уменьшится практически до нуля за время 
.
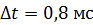246. По катушке индуктивностью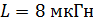 
течет ток 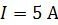. Определите среднее значение ЭДС самоиндукции 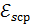, возникающей в контуре, при уменьшении силы тока практически до нуля за время 
.
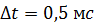247. В электрической цепи, содержащей резистор сопротивлением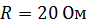 
и катушку индуктивностью 
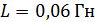, течет ток 
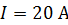. Определите направление и величину индукционного тока I в цепи через время 
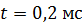после отключения источника тока без разрывания цепи.
248. Цепь состоит из катушки индуктивностью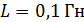 
и источника тока. Источник отключили, не разрывая цепи. За время 
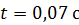сила тока уменьшилась до 
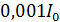, где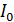 
– начальное значение. Определите активное сопротивление катушки 
.
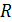249. Источник тока замкнули на катушку сопротивлением 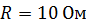и индуктивностью 
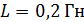. За какое время 
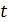ток в цепи достигнет величины, равной 
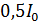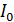, где – установившееся значение? Покажите направление индукционного тока в катушке.
250. Источник тока замкнули на катушку сопротивлением 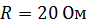. За время 
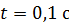, прошедшее от момента замыкания, сила тока в катушке достигла 
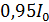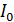, где – установившееся значение. Покажите направление индукционного тока в катушке и определите индуктивность катушки .
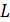КОНТРОЛЬНАЯ РАБОТА № 3
Студент решает 6 задач своего варианта, номер которого совпадает с последней цифрой шифра. Номера задач каждого варианта представлены в табл. 10.
6.1. Таблица вариантов контрольной работы № 3
Таблица 10
| Вариант | Номера задач | |||||
| 0 | 310 | 320 | 330 | 340 | 350 | 360 |
| 1 | 301 | 311 | 321 | 331 | 341 | 351 |
| 2 | 302 | 312 | 322 | 332 | 342 | 352 |
| 3 | 303 | 313 | 323 | 333 | 343 | 353 |
| 4 | 304 | 314 | 324 | 334 | 344 | 354 |
| 5 | 305 | 315 | 325 | 335 | 345 | 355 |
| 6 | 306 | 316 | 326 | 336 | 346 | 356 |
| 7 | 307 | 317 | 327 | 337 | 347 | 357 |
| 8 | 308 | 318 | 328 | 338 | 348 | 358 |
| 9 | 309 | 319 | 329 | 339 | 349 | 359 |
Рекомендации к решению задач по разделу «Оптика»
1. Текст задачи следует внимательно прочитать, чтобы выяснить, какое физическое явление рассматривается в задаче. Полезно изобразить схематический чертеж или рисунок.
2. Ознакомьтесь с основными формулами для данного явления. Выясните, можно ли применить законы сохранения (ЗСИ, ЗСЗ, ЗСЭ) – для этого проверьте, выполняются ли в задаче условия применения закона. Выпишите законы и формулы, пригодные для решения данной задачи.
3. Запишите краткое условие задачи, выбирая для обозначения данных и искомых величин символы, которые будут использованы в формулах.
4. Задачу следует решать, как правило, в общем виде, чтобы получить расчетную формулу определяемой величины, содержащую символы заданных величин и физических постоянных.
5. Вычисление определяемой величины начинайте с подстановки в расчетную формулу значений величин. При этом следует помнить, что большинство физических величин имеют свои единицы измерения. Полезно записывать их при подстановке в формулу, чтобы убедиться, что все величины взяты в единицах СИ. Только при вычислении отношений, например, 
и т. п. можно подставлять значения величин в любых, но одинаковых единицах, т. е. не обязательно в СИ. Если определяемых величин несколько, то вывод расчетной формулы для следующей величины начинайте, закончив вычисление предыдущей.
6. Полезно выполнять проверку расчетной формулы на совпадение единиц измерения левой и правой части равенства. Несовпадение единиц указывает на ошибку в расчетной формуле.
7. Вычисление и запись результата делайте с точностью до двух или трех (не более) значащих цифр. Незначащие нули записывайте в виде сомножителя 
. При этом, если показатель степени n соответствует приставке, используйте её: например, 
; 
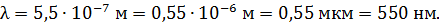Помните, что точность результата вычислений не может быть выше, чем точность исходных данных. Рекомендации по выполнению расчетов при решении задач подробно изложены в п. 1.7 (см. с. 27-29).
8. Оцените разумность полученного значения искомой величины одним из следующих путей: а) по физическому смыслу; б) сравнением с табличным значением или, по порядку величины, с числами, приведенными в рекомендациях к решению задач по данной теме.
Рекомендации к решению задач по разделу
«Атомная и ядерная физика»
1. В стационарных состояниях атома параметры электрона: радиус круговой орбиты, скорость электрона и его момент импульса, период обращения, энергия электрона, – имеют дискретные значения, которые определяются главным квантовым числом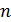 
(номер орбиты). Эта зависимость отражается индексом величин: 
.
2. По мере увеличения номера орбиты 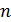ее радиус увеличивается 
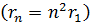, а скорость электрона уменьшается 
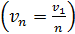; в результате период обращения растет 
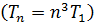, возрастает момент импульса электрона 
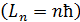и увеличивается его энергия 
.
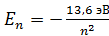3. Порядок величин параметров электрона в атоме водорода можно оценить по указанным зависимостям и значениям величин для основного состояния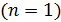 
. В этом состоянии радиус орбиты 
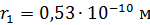, скорость электрона 
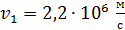, период обращения 
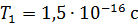, момент импульса 
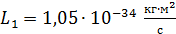, и полная энергия электрона 
.
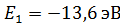4. Рекомендации по выполнению расчетов при решении задач подробно изложены в п. 1.7 (см. стр. 27-29).
Интерференция света
301. Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой с радиусом кривизны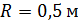 
находится некоторая жидкость. При наблюдении в отраженном свете с длиной волны 
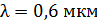измерен радиус третьего темного кольца Ньютона: 
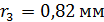. Определите показатель преломления 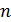жидкости.
302. На тонкую пленку по нормали к ее поверхности падает монохроматический свет с длиной волны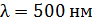 
. Отраженный от пленки свет максимально усилен вследствие интерференции. Определите минимальную толщину пленки 
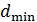, если показатель преломления материала пленки 
.
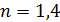303. В опыте Юнга расстояние от щелей до экрана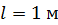 
; длина волны света 
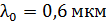. Определите расстояние 
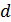между щелями, если на участке экрана длиной 
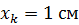укладывается 
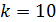темных интерференционных полос.
304. На стеклянную пластинку положена выпуклой стороной плосковыпуклая линза. Сверху линза освещена монохроматическим светом с длиной волны 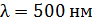. Определите радиус линзы 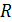, если радиус четвертого темного кольца Ньютона в отраженном свете 
.
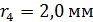305. На тонкую глицериновую пленку с показателем преломления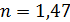 
и толщиной 
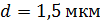падает белый свет по нормали к поверхности пленки. Определите длины волн 
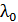лучей видимого участка спектра ( 
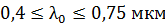), которые в отраженном свете будут ослаблены в результате интерференции.
306. На стеклянную линзу объектива с показателем преломления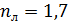 
нанесена тонкая прозрачная пленка вещества с показателем преломления 
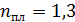. Объектив освещен падающим на него нормально пучком света с длиной волны 
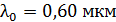. Определите наименьшую толщину пленки 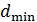, при которой отраженный свет будет иметь минимальную интенсивность.
307. На тонкий стеклянный клин с показателем преломления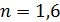 
падает нормально параллельный пучок света с длиной волны 
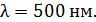Расстояние между соседними темными интерференционными полосами в отраженном свете 
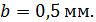Определите угол 
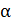между поверхностями клина.
308. Плосковыпуклая стеклянная линза с радиусом кривизны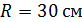 
лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца Ньютона в отраженном свете 
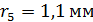. Определите длину световой волны 
.
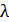309. Между двумя плоскопараллельными пластинками на расстоянии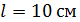 
от линии их соприкосновения находится проволока диаметром 
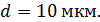Пластинки, образующие воздушный клин, освещаются нормально падающим монохроматическим светом с длиной волны 
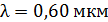. Определите ширину 
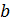интерференционных полос, наблюдаемых в отраженном свете.
310. Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом с длиной волны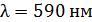 
. Определите толщину воздушного промежутка 
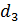в том месте, где в отраженном свете наблюдается третье светлое кольцо.
Дифракция света
311. Какое наименьшее число щелей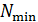 
должна содержать дифракционная решетка, чтобы в спектре второго порядка можно было видеть раздельно две желтые линии натрия с длинами волн 
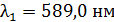и 
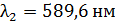? Определите длину 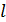такой решетки, если постоянная решетки 
?
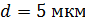312. На поверхность дифракционной решетки по нормали падает монохроматический свет. Постоянная дифракционной решетки 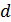в 4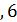 
раза больше, чем длина световой волны 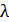. Определите общее число 
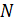дифракционных максимумов, которые теоретически можно наблюдать в данном случае.
313. На дифракционную решетку по нормали к ней падает параллельный пучок белого света. Спектры третьего и четвертого порядка частично накладываются друг на друга. Определите длину волны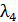 
спектральной линии в спектре четвертого порядка, на которую накладывается линия границы спектра третьего порядка: 
?
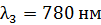314. На дифракционную решетку, содержащую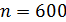 
штрихов на одном миллиметре длины, падает нормально белый свет. Линзой, помещенной вблизи решетки, дифракционный спектр проецируется на экран. Определите длину 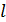спектра первого порядка на экране, если расстояние от линзы до экрана 
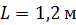. Длины волн границ видимого спектра: 
, 
.
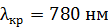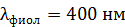315. На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения. Расстояние между атомными плоскостями кристалла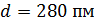 
. Дифракционный максимум первого порядка наблюдается под углом 
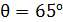к атомной плоскости. Определите длину волны рентгеновского излучения .
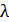316. На диафрагму с узкой щелью падает нормально плоская монохроматическая световая волна с длиной волны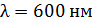 
. Угол дифракции лучей, соответствующих второму дифракционному максимуму, 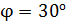. Определите ширину щели 
.
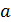317. На дифракционную решетку, содержащую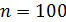 
штрихов на одном миллиметре длины, падает нормально монохроматический свет. Зрительная труба спектрометра наведена на максимум второго порядка: 
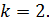Чтобы навести трубу на другой максимум того же порядка 
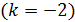, ее нужно повернуть на угол 
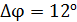. Определите длину волны 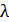света, падающего на решетку.
318. Дифракционная решетка длиной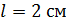 
позволяет разрешить в спектре первого порядка две спектральные линии калия: 
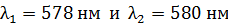. Определите общее число щелей 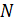этой решетки и ее постоянную .
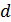319. Постоянная дифракционной решетки 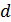в 4 раза больше, чем длина световой волны монохроматического света 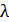, падающего нормально на ее поверхность. Определите угол 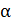между первыми симметричными дифракционными максимумами.
320. На дифракционную решетку, постоянная которой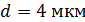 
, падает нормально свет с длиной волны 
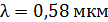. Определите наибольший порядок максимума 
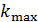, который дает эта решетка, и угол дифракции 
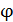для этого максимума ( ).
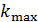Тепловое излучение
321. Вычислите истинную температуру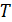 
раскаленной вольфрамовой ленты, если радиационный пирометр показывает температуру 
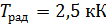. Считайте, что поглощательная способность вольфрама 
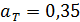и не зависит от длины волны излучения.
322. Температура абсолютно черного тела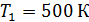 
. Какова будет температура тела 
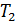, если в результате нагревания поток излучения увеличится в 
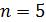раз?
323. Температура абсолютно черного тела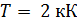 
. Определите длину волны 
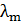, на которую приходится максимум энергии излучения, и спектральную плотность энергетической светимости 
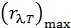для этой длины волны.
324. Определите температуру 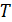и энергетическую светимость 
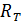абсолютно черного тела, если максимум энергии излучения приходится на длину волны 
.
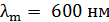325. Из смотрового окна печи излучается поток энергии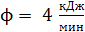 
. Определите температуру 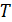печи, если площадь окна 
.
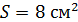326. Поток излучения абсолютно черного тела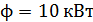 
. Максимум энергии излучения приходится на длину волны 
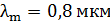. Определите площадь 
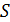излучающей поверхности.
327. Как и во сколько раз изменится поток излучения 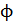абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра: 
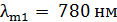, на фиолетовую границу – 
?
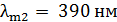328. Длина волны, на которую приходится максимум энергии излучения абсолютно черного тела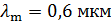 
. Определите температуру тела .
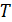329. Муфельная печь, потребляющая мощность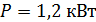 
, имеет отверстие площадью 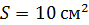. Определите долю 
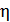мощности, которая рассеивается стенками печи, если температура ее внутренней поверхности 
.
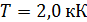330. Средняя энергетическая светимость поверхности Земли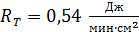 
. Определите температуру 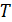поверхности Земли, принимая, что она излучает как серое тело, имеющее поглощательную способность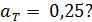 
Фотоэффект
331. Красная граница фотоэффекта для цинка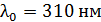 
. Определите максимальную кинетическую энергию фотоэлектронов 
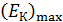в джоулях и в электрон-вольтах, если на фотокатод падает свет с длиной волны 
.
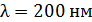332. На поверхность калия падает свет с длиной волны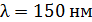 
. Определите максимальную кинетическую энергию фотоэлектронов .
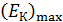333. Фотон с энергией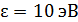 
падает на серебряную пластинку и вызывает фотоэффект. Определите импульс 
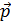, полученный пластинкой, принимая, что скорости движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластинки.
334. На фотоэлемент с катодом из лития падает свет с длиной волны 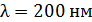. Определите наименьшее значение задерживающей разности потенциалов 
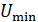, которую нужно приложить к фотоэлементу, чтобы фототок стал равен нулю.
335. Какова должна быть длина волны 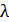рентгеновского излучения, падающего на платиновую пластинку, чтобы максимальная скорость фотоэлектронов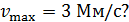 
336. На металлический фотокатод направлен пучок ультрафиолетового излучения с длиной волны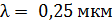 
. Фототок прекращается, если приложить минимальную задерживающую разность потенциалов 
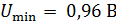. Определите работу выхода 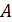электронов из металла.
337. Излучение с длиной волны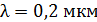 
падает на поверхность металла. Красная граница фотоэффекта для него 
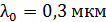. Определите долю энергии фотона, которая расходуется на сообщение электрону кинетической энергии .
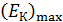338. На металлический катод падает рентгеновское излучение с длиной волны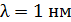 
. Пренебрегая работой выхода, определите максимальную скорость фотоэлектронов 
.
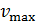339. На металлическую пластинку направлен пучок света с частотой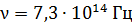 
. Красная граница фотоэффекта для данного металла 
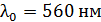. Определите максимальную скорость фотоэлектронов .
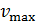340. На цинковую пластинку направлен монохроматический пучок света. Фототок прекращается при задерживающей разности потенциалов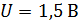 
. Определите длину волны 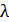света, падающего на пластинку.
КОНТРОЛЬНАЯ РАБОТА № 2
Студент решает 6 задач своего варианта, номер которого совпадает с последней цифрой шифра. Номера задач каждого варианта представлены в табл. 9.
5.1. Таблица вариантов контрольной работы № 2
| Вариант | Номера задач | |||||
| 0 | 210 | 220 | 230 | 240 | 250 | 260 |
| 1 | 201 | 211 | 221 | 231 | 241 | 251 |
| 2 | 202 | 212 | 222 | 232 | 242 | 252 |
| 3 | 203 | 213 | 223 | 233 | 243 | 253 |
| 4 | 204 | 214 | 224 | 234 | 244 | 254 |
| 5 | 205 | 215 | 225 | 235 | 245 | 255 |
| 6 | 206 | 216 | 226 | 236 | 246 | 256 |
| 7 | 207 | 217 | 227 | 237 | 247 | 257 |
| 8 | 208 | 218 | 228 | 238 | 248 | 258 |
| 9 | 209 | 219 | 229 | 239 | 249 | 259 |
Таблица 9
Рекомендации к решению задач по разделу «Электромагнетизм»
1. Внимательно прочитайте условие задачи. Выясните, какое явление рассматривается в задаче, и изучите сведения о нем и о физических величинах, его описывающих, по учебному пособию.
2. При определении магнитных сил, магнитного потока и других величин обратите внимание на то, какое магнитное поле рассматривается в задаче – однородное или неоднородное. В первом случае используйте более простые формулы для однородного МП.
3. При решении задачи определяйте направления искомых векторов 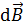, 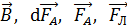и др. Для этого используйте а) определительные формулы, в правой части которых записано векторное произведение векторов или б) правило буравчика и правило левой руки.
4. В том случае, если магнитное поле создается в ферромагнетике, для которого магнитная проницаемость 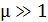(в отличие от картонного или воздушного сердечника, имеющего 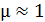), необходимо определять величину 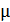по формуле, связывающей напряженность 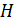и магнитную индукцию :
.
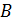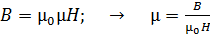При этом следует учесть, что величина магнитной индукции зависит от напряженности МП: 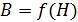, – и соответственно 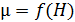. Поэтому сначала вычисляют напряженность магнитного поля 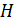, которая зависит только от тока в контуре и формы и размеров контура (катушки). Затем по экспериментальному графику кривой намагничивания 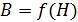для заданного материала сердечника (используя справочные данные) по рассчитанной величине 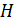определяют индукцию магнитного поля 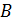. По найденным значениям 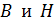вычисляют магнитную проницаемость сердечника по записанной выше формуле.
ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ № 2
Дата: 2019-03-05, просмотров: 200.
