Звук передається коливаннями частинок повітря. Щоб частинки повітря могли зробити звукові коливання, необхідно, щоб вони якимсь чином були приведені в коливальний стан або, як прийнято говорити в акустиці, були “збуджені”. Таким збудником або, інакше кажучи, джерелом звуку може бути, наприклад, дифузор гучномовця, струна скрипки і т.п. Тут коливання твердих тіл (дифузор, струна) викликають коливання частинок повітря.
Тверде тіло або сукупність декількох твердих тіл, що беруть участь в коливаннях, називається механічною коливальною системою. Рух цих тіл характеризується або переміщенням x якої-небудь точки тіла, або швидкістю цієї крапки, або це прискоренням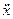 
.
Розглянемо просту механічну коливальну систему (рис. 12.1), що складається з маси т, укріпленою на пружині що має пружність s.
Рис. 12.1 - Проста механічна коливальна система
Маса знаходиться у в'язкому середовищі, що створює опір тертя r. Якщо кінець пружини відтягнутий з положення рівноваги на відстань х, то пружина прагне скоротитися з деякою силою. Очевидно, що ця сила тим більше, чим на більшу відстань відтягнута пружина і чим більше її пружність. Звідси повертаюча сила пружини Fs, прагнуча повернути відтягнутий її кінець в положення рівноваги, рівна твору хs, де х — відстань, на яку відтягнутий кінець пружини, а s — коефіцієнт пружності пружини.
У свою чергу s визначається як s = Fs/x.
Звідси одиницею пружності називається пружність такої пружини, яка при розтягуванні на одиницю довжини (1 м) прагне скоротитися з силою, рівній також одиниці (1 Н - одиниця сили в системі СИ - 1 ньютон (Н)).
Властивості пружини можна характеризувати і величиною, зворотною коефіцієнту, пружності. Ця величина називається коефіцієнтом гнучкості і позначається буквою с: с=1/s і відповідно с=х/Fs.
При переміщенні тіла виникають сили тертя, гальмуючі рух тіла. При русі тіла у в'язкому середовищі значення сили тертя Fr пропорційно швидкості тіла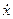 
і коефіцієнту r, що характеризує середовище, в якому виникає тертя, і званому зазвичай опором тертя. Слід відмітити, що опір тертя може виникати не тільки при русі тіла у в'язкому середовищі, але і в результаті внутрішнього тертя, наприклад, тертя частинок в товщі матеріалу пружини при її розтягуванні або стисненні.
Опір тертя - одна з складових активного механічного опору. Характерною особливістю реальної механічної системи (що володіє активним механічним опором) є те, що в ній завжди має місце необоротний перехід механічної енергії в теплову.
Сила тертя може бути виражена як Fr=r 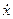або r=Fr/ .
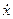Одиницею активного опору (тертя) називається такий опір, який при переміщенні тіла з швидкістю, рівній одиниці (1 м/с), викликає гальмуючу силу, рівну також одиниці (1 Н). Одиниця активного опору вимірюється в кГ/с (якщо врахувати розмірність сили кГ∙м/с2).
Всі тіла прагнуть зберегти стан спокою або рівномірного прямолінійного руху. Зміні цього стану вони чинять опір з силою інерції, рівної твору маси на прискорення.
Хай до тіла з масою т (див. рис. 12.1) прикладена сила F, направлена вниз. Під впливом цієї сили тіло опуститься на відстань х від положення рівноваги. При цьому, окрім зовнішньої сили F, на тіло масою т діють наступні сили: по-перше, сила інерції т 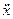, по-друге, гальмуюча сила тертя, рівна r 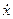, по-третє, сила пружності пружини sх, яка прагне повернути тіло в положення рівноваги. Процес в такій механічній системі подібний до процесу в ланцюзі змінного струму, індуктивності L, що складається з послідовного з'єднання, активного опору R і ємності С.
Цю подібність відображає той факт, що в обох системах має місце перетворення енергії з одного вигляду в іншій. Дійсно, в механічній системі кінетична енергія рухомого тіла перетворюється на потенційну енергію розтягнутої пружини, і назад. Частина енергії із-за наявності тертя переходить в тепло. У електричному ланцюзі енергія магнітного поля, що з'являється при проходженні електричного струму, перетворюється на енергію електричного поля (заряд конденсатора), і назад. Частина енергії виділяється на активному опорі у вигляді тепла. Тому маса, опір тертя і гнучкість аналогічні відповідно індуктивності, активному опору і електричній ємкості. Ця подібність не є чисто зовнішньою, формальною, а відображає фізичну подібність даних величин або, як їх називають, параметрів. Дійсно, індуктивність в ланцюзі перешкоджає як миттєвому зростанню струму від нуля до якогось кінцевого його значення при включенні джерела напруги, так і спаду струму до нуля відразу ж при виключенні напруги. То ж відноситься до маси в механічній системі. Інертність тіла перешкоджає миттєвому наростанню швидкості при додатку сили і не дає тілу зупинитися відразу.
Як вже наголошувалося, частина енергії електричного струму завдяки наявності активного опору перетворюється на тепло. Також перетворюється на тепло за наявності тертя частина механічної енергії. Чим більше гнучкість пружини, тим більший зсув вона отримує при заданому значенні сили. Чим більше електрична ємкість, тим більший заряд створюється на конденсаторі при заданій прикладеній напрузі. Заряд можна розглядати як аналог зсуву, а струм, отже, як аналог швидкості. Аналогічні також електрорушійна, сила і механічна сила, перша є причиною проходження струму, друга, - рухи тіла.
Звідси аналогічно коливальна швидкість тіла в простій коливальній системі, на яку діє сила F, змінна по синусоїдальному закону з круговою частотою ω, виражається таким чином:
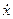=F/zM=F/[r+j( ωm-s/ω)]. (12.1)
а її модуль:
.
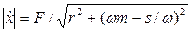Це аналогічно:
.
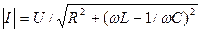Як:
.
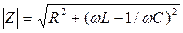є повним електричним опором, вимірюваним в омах, так:
.
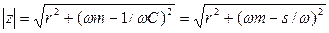Є повним електричним опором, вимірюваним в механічних омах (мехомах).
Подібно до реактивного опору електричний ланцюгу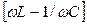 
, такий, що є різницею індуктивного ωL і ємкісного 1/(ωC) опорів, в механічній системі опір 
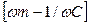називається реактивним механічним опором і є різницею інерційного опору ωm (обумовленого інертністю тіла) і пружного опору 1/(ωc) або s/ω. Механічний реактивний опір також вимірюється в мехомах.
У електротехніці і акустиці величини (сила, зсув, швидкість, прискорення і т. ін.), що синусоїдальний змінюються, прийнято змінювати в значеннях, що діють, які в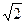 
раз менше амплітудних. Вкажемо, що абсолютні значення амплітудних (і що відповідно діють) значень зсуву x, швидкості 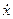і прискорення 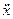зв'язані між собою співвідношеннями:
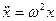; або 
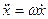; і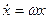 
.
Надалі, якщо не обмовлятиметься інше, ми користуватимемося значеннями, що саме діють, цих і інших величин.
Зсув при коливальному русі вимірюється в звичайних одиницях довжини (м), коливальна швидкість - в звичайних одиницях швидкості (м/с), а прискорення при цьому русі - в звичайних одиницях прискорення (м/с2).
З приведених співвідношеннях можна зробити вивід, що для досягнення однієї і тієї ж амплітуди коливальної швидкості 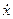потрібний малий зсув на високій частоті коливань і великий зсув на низькій частоті.
Розглядаючи вираз для швидкості при різних значеннях частоти, бачимо, що якщо реактивний механічний опір рівний нулю, то швидкість буде максимальною. Це відбудеться на частоті, званою частотою резонансу, яка для механічної системи:
.
Отже, резонансна частота механічної системи буде тим вище, чим більше її пружність і менше маса, тобто ніж жорстокішою і легшою виявиться система. Навпаки, чим важче і гнучкіше система, тим нижче її власна частота. Це підтверджується повсякденним досвідом. Жорстка легка сталева смужка, затиснута в лещатах, має високу резонансну частоту. Велика маса на гнучких амортизаторах, наприклад автомашина на ресорах, має низьку резонансну частоту.
Неважко бачити, що поблизу резонансу швидкість системи, по суті, визначається активним опором (опором тертя), оскільки в цій області реактивний опір вельми мало і їм можна нехтувати в порівнянні з активним. Якщо активний опір в системі невеликий, то в області частот нижче резонансною коливальна швидкість визначається в основному пружністю або, точніше, пружним опором s/ω, а в області частот вище резонансною — масою або, точніше, інерційним опором mω. У першому випадку повний механічний опір визначається пружним, а в другому — інерційним опором. Відповідно до цього говорять, що система управляється пружністю, масою або активним опором.
Аналогія між механічною коливальною системою і електричним ланцюгом дозволяє зображати механічні системи за допомогою аналогічних їм електричних схем, розраховувати і досліджувати схеми і отримані результати знов перекладати мовою механічних величин. Цей прийом називається методом електромеханічних аналогій і широко використовується в електроакустиці.
Розібрана аналогія між простій механічною коливальною системою і послідовним з'єднанням індуктивності, ємкості і активного опору є простою. На практиці доводиться зустрічатися з набагато складнішими системами і аналогіями. Особливо важко те, що підшукало аналогів, коли механічна система складається не із зосереджених мас, пружностей, опорів, а з розподілених, що має місце, наприклад, в струнах, що коливаються, мембранах, пластинках, балках і т. п., де кожен малий елемент тіла, що коливається, володіє і масою, і пружністю, і тертям.
Щоб показати, як складаються схеми аналогії, розглянемо наступний приклад. Дана механічна система (рис. 12.2), що складається з мас т1 і т2, які сполучені пружиною, гнучкістю, що володіє, с. На масу т1 діє сила F.
Рис. 12.2 - Механічна коливальна система 
Оскільки електричною аналогією сили є е.д.с, то в схемі аналогії сила відображається е.д.с, що діє безпосередньо на масу m1. Після маси m1 слідують елементи с і т2, які можна сполучати або послідовно, або паралельно. Якщо вони сполучені послідовно, то при дуже малому значенні гнучкості з пружний опір великий, і, отже, струму в ланцюзі не буде. У перекладі мовою механіки це означає, що, не дивлячись на прикладену силу, система не коливається. Разом з тим мале значення гнучкості означає, що маси т1 і т2 жорстко сполучені, як би зливаються в одну масу, що не допускає відсутності коливань в системі.
З'єднаємо тепер с і т2 паралельно (рис. 12.3).
Рис. 12.3 - Схема аналогії механічної коливальної системи по рис. 12.2.
При такому з'єднанні мале значення гнучкості с ніяк не перешкоджає коливанням в системі. Якщо, навпаки, покласти, що з вельми велике (дуже слабка пружина, волосок), то малий пружний опір зашунтує в схемі аналогії т2 і ця маса при цьому коливатися не буде. До цього ж висновку можна прийти і не удаючись до схеми аналогії. Дійсно, якщо сила діє на масу m1, то її коливання практично не передаватимуться масі т2, якщо вона сполучена з масою m1, за допомогою дуже гнучкої (малопружною) пружини. Таким чином, додаючи параметрам механічної системи або дуже великі, або дуже малі значення, можна переконатися в тому, що схема аналогії (рис. 12.3) складена правильно.
Вживані в електроакустиці апарати є перетворювачами одного виду енергії в іншій. Наприклад, що підводиться до затисків гучномовця електрична енергія частково витрачається на нагрів провідника і, таким чином, перетворюється на теплову, а частково перетворюється на механічну енергію коливань рухомої системи гучномовця. Для з'ясування суті процесу перетворення одного виду енергії в іншій і зв'язку між електричним ланцюгом і механічною коливальною системою перетворювача розглянемо для прикладу найбільш поширений в електроакустиці електродинамічний принцип перетворення.
З електротехніки відомо, що якщо помістити в магнітне поле провідник із струмом, то він почне рухатися в напрямі, визначуваному правилом лівої руки. Наприклад, хай провідник має форму плоского витка, в якому струм направлений за годинниковою стрілкою, а магнітні силові лінії направлені по радіусах від центру витка. Тоді сила, яка діє на виток, виявиться направленою вгору. При зміні напряму струму на зворотне сила, що діє на виток, також змінить свій напрям. Тому, якщо в провіднику протікатиме змінний струм, то провідник коливатиметься. Навпаки, якщо виток, що знаходиться в магнітному полі, коливається під впливом якої-небудь сили, що діє на нього, і перерізує при цьому магнітні силові лінії, то в нім індукуватиметься е.р.с. Якщо виток замкнути, то в ланцюзі потече струм. Розглянемо декілька докладніше явища, що відбуваються при електродинамічному способі перетворення.
Якщо прикласти до котушки, що складається з декількох витків і знаходиться в магнітному полі, змінна напруга U, то вона починає коливатися під дією виникаючих сил. При цьому у витках котушки, яка перетинає магнітні силові лінії, індукується е.р.с. Напрям е.р.с. за правилом Ленца таке, щоб протидіяти причині, що її викликала, тобто прикладеній напрузі. Значення протилежне е.р.с. рівне В1 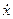, де В - магнітна індукція, Тл; l - довжина провідника котушки; м; 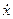- швидкість руху котушки, м/с. Якщо позначити електричний опір котушки через R, то за законом Ома струм в ній:
I=(U-Bl 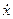)/R.
Електростатичний перетворювач складається з нерухомого і рухомого обкладань, що знаходяться на відстані d. При додатку до них постійної напруги U0 і змінної напруги частоти ω рухоме обкладання почне коливатися з тією ж частотою. Коефіцієнт електромеханічного зв'язку буде:
K=U0/(ωd). (12.2)
Для п'єзоелектричного перетворювача з деформацією, яка гнеться, що є пластинкою довжиною l і товщиною h, що коливається при додатку до неї змінної напруги частоти ω коефіцієнт електромеханічного зв'язку буде:
.
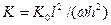де К0 — коефіцієнт п'єзоефекту.
Розглянемо процес виникнення і розповсюдження коливань в повітряному середовищі.
Хай є нескінченно велика жорстка стінка C, в якій може пересуватися управо і вліво щодо свого положення рівноваги поршень П (рис. 12.4). Хай, наприклад, в даний момент поршень йде управо, штовхаючи частинки повітря, що знаходяться перед ним. Частинки, відхиляючись від свого положення рівноваги, у свою чергу штовхають частинки, що знаходяться вправо від них, тобто наступні за ними і т. ін. Праворуч від поршня утворюється згущування повітря або область з підвищеним атмосферним тиском. Поштовхи від однієї частинки повітря до іншої передаються все далі від поршня, унаслідок чого вправо від нього розповсюджується згущування. Хай тепер поршень після того, як він досяг свого крайнього правого положення, почав пересуватися вліво. Тоді перед ним утворюється розрідження повітря, або область із зниженим атмосферним тиском. Оскільки у поверхні поршня створилася область розрідження, туди направляться частинки повітря, що примикають до неї. На тому місці, де вони знаходилися, у свою чергу образу утворюється область розрідження, в яку направляться інші, що примикають до цієї області, частинки повітря. В результаті вправо від поршня розповсюджуватиметься розрідження. Таким чином, коливання поршня періодично викликають в зовнішньому середовищі (повітрі) обурення у вигляді згущування і розрідження, причому одному періоду коливань (рух поршня вперед і назад) відповідає одне згущування і одне розрідження.
Тиск р, зміряне в якійсь певній точці середовища, що оточує поршень, змінюється залежно від часу згідно із законом, подібному закону руху поршня. При коливальному русі поршня тиск в даній крапці спочатку наростає, стаючи більше атмосферного тиску p0, а потім спадає до значення меншого, ніж атмосферний тиск, і, нарешті, знову збільшується до значення р0.
Графічно процес зміни тиску в часі в даній точці середовища зображений на рис. 12.5, який відповідає руху поршня, що здійснюється по синусоїдальному закону. Значення тиску в кожен момент часу називається його миттєвим значенням. Тиск в кожній даній крапці можна представити у вигляді суми два складових: постійною, рівною атмосферному тиску, і що накладається на нього змінною. Остання зазвичай називається звуковим тиском. Період зміни тиску Т рівний періоду коливань поршня. Амплітуда ж звукового тиску пропорційна амплітуді коливань поршня. Відмітимо, що на рис. 12.5 амплітуда звукового тиску сильно перебільшена в порівнянні із значенням атмосферного тиску із-за неможливості зобразити величини тиску в дійсному співвідношенні, оскільки амплітуда звукового тиску навіть найгучніших звуків складає менше однієї тисячної частки від величини атмосферного тиску.
 |
Рис. 12.4 - Утворення звукових хвиль у середовищі
Рис. 12.5 - Залежність тиску у середовищі від часу
Звуковий тиск, як і всякий тиск, вимірюється силою, площі, що діє на одиницю. Тому в акустиці за одиницю звукового тиску прийнятий такий тиск, при якому на площу в 1 м2 діє сила, рівна 1 Н. Ця одиниця звукового тиску називається паскаль (Па). Паскаль є зручною одиницею вимірювання, оскільки в більшості випадків значення звукового тиску змінюються від сотих доль паскаля до декількох його одиниць. Звуковий тиск при середній гучності розмови складає долі Паскаля. Середній атмосферний тиск, відповідний тиску ртутного стовпа висотою 760 мм, складає приблизно 105 Па.
Як і інші акустичні величини, звуковий тиск також вимірюється в значеннях, що діють.
Стан середовища в даній крапці можна охарактеризувати не тільки зміною тиску в ній, але і швидкістю частинок повітря або зсувом їх щодо положення рівноваги. При синусоїдальних коливаннях поршня криві швидкості або зсуви частинок залежно від часу мають також синусоїдальну форму.
На рис. 12.6 зображена зміна в часі швидкості частинок, зазвичай званою в акустиці коливальною швидкістю. Коливальна швидкість 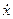в різні моменти часу має різні значення і знаки. Таким чином, в звуковому полі кожна частинка середовища знаходиться в певній фазі коливань.
Отже, коливання джерела звуку (наприклад, поршня) викликають в середовищі згущування і розрідження. Область, в якій спостерігаються згущування і розрідження, називається звуковим полем. Згущування і розрідження розповсюджуються в середовищі з певною швидкістю, званою швидкістю розповсюдження звуку.
Її значення залежить від характеру і стану середовища. Так, швидкість звуку в газовому середовищі:
.
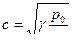де р0 - постійний (атмосферний) тиск; γ; - показник адіабати, тобто відношення теплоємності газу при постійному тиску до теплоємності газу при постійному об'ємі. Це відношення для повітря рівне 1,4; р — щільність повітря, рівна при 0°С і 760 мм рт. ст. 1,3 кг/м3
Рис. 12.6 - Залежність коливальної швидкості у середовищі від часу
Рис. 12.7 - Залежність звукового тиску від відстані до джерела
Для повітря за цих умов швидкість розповсюдження звуку рівна 331 м/с, а при 20°С вона підвищується до 344 м/с.
Швидкість звуку жодним чином не слід змішувати з коливальною швидкістю частинок середовища. Коливальна швидкість частинок середовища залежно від різних умов (наприклад, від амплітуди, частоти коливань джерела звуку) може мати різні значення, при цьому у багато разів менші швидкості розповсюдження звуку. Процеси коливань частинок середовища і розповсюдження звуку різні і по суті. Тоді як звук за відсутності перешкод може розповсюджуватися в середовищі скільки завгодно далеко від джерела, частинки середовища коливаються біля свого положення рівноваги і поступальної ходи не мають.
Якщо одночасно зміряти звуковий тиск в різних точках прямої у напрямі розповсюдження звуку, то за допомогою набутих значень можна побудувати криву залежності звукового тиску р від відстані r. При синусоїдальних коливаннях джерела звуку ця крива має показану на рис. 12.7 форму, також близьку до синусоїди. Правда, отримана крива відрізнятиметься від ідеальної синусоїди: подальші амплітуди її зменшуються у міру видалення від джерела в результаті того, що енергія звуку розподіляється на все велику поверхню і поглинається в самому середовищі.
Кожній крапці, розташованій на кривій, відповідає своя фаза коливання. Проте можна вказати деяке число крапок з рівними фазами. Так, наприклад, в точках a1, a2, a3 має місце максимум звукового тиску. Однією і тією ж фазою характеризуються також коливання в точках 61, б2, б3. Яка ж відстань розділяє крапки з однаковою фазою? Відомо, що за один період джерело звуку посилає в середу одне згущування і одне розрідження. Розглядаючи рис. 12.7, бачимо, що відрізок а1а2 або б1б2 рівний відрізку в1в2, тобто відрізку, в якому укладається одне розрідження і одне згущування. Оскільки згущування і розрідження переміщаються із швидкістю звуку, то за час Т, рівне одному періоду, звукові коливання розповсюджуються на відстань:
λ=cT або λ=c/f . (12.3)
Відстань λ між найближчими крапками (наприклад, В1В2), в яких коливання знаходяться в одній і тій же фазі, називається довжиною хвилі. Так, для частот звуку від 50 до 10 000 Гц довжини хвилі в повітрі змінюються від 6,8 м до 3,4 див.
Різниця фаз між крапками, розділеними відстанню пλ, рівна 2πn, де n — ціле число. Різниця фаз φ між крапками, що знаходяться на відстані l, може бути знайдена із співвідношення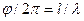 
. Звідси:
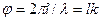. (12.4)
де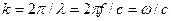 
.
Величина k в акустиці зазвичай називається хвильовим числом. Через всі крапки, в яких коливання знаходяться в одній фазі, можна провести поверхню. Ця поверхня називається хвильовою або фронтом хвилі. Залежно від форми, яку має поверхню фронту хвилі, розрізняють хвилі сферичні, плоскі і т.д. Уявимо собі джерело звуку у вигляді пульсуючої кулі, наприклад гумової оболонки, в яку поперемінно нагнітається і з якої відкачується повітря. Таке джерело звуку посилає в середу згущування і розрідження рівномірно на всі боки, порушуючи сферичні хвилі. Але на великій відстані від джерела окремі ділянки поверхні фронту сферичної хвилі можна вважати плоскими.
Практичні джерела звуку зазвичай не дають ні тій ні іншої форми хвилі в чистому вигляді. При збудженні звукових хвиль енергія від джерела поступає в середу. Завдяки цій енергії виникають коливальні рухи частинок середовища. Енергія цих коливань може передаватися тілам, поміщеним в звукове поле. Енергію звукового поля можна характеризувати кількістю енергії, що проходить через одиницю площі, розташованої в полі перпендикулярно напряму розповсюдження звуку за одиницю часу (рис. 12.8). Ця величина називається інтенсивністю звуку і вимірюється у ватах на квадратний метр.
Для сферичної хвилі по заданій інтенсивності на заданій відстані від джерела легко визначити потужність джерела. Дійсно, на відстані r від джерела відповідна сферична поверхня рівна 4πr2. Якщо через кожен квадратний метр цієї поверхні проходить потужність I, то потужність, що проходить через всю поверхню, складе 4πr2I. Цю потужність Р повинне доставити джерело.
Отже:
P=4πr2I или I=P/(4πr2). (12.5)
Інтенсивність в сферичній хвилі назад пропорційна квадрату відстані від джерела. Але інтенсивність пов'язана із звуковим тиском в сферичній хвилі співвідношенням I=p2/(ρc), тут ρc — хвильовий або питомий акустичний опір середовищу, що є твором щільності середовища ρ на швидкість звуку с в ній. Для повітря при 20°С і 760 мм рт. ст. ρс=415 кг/(с∙м2)
Враховуючи це, отримуєм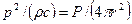о: 
або:
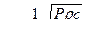. (12.6)
тобто, звуковий тиск в сферичній хвилі обернено пропорційно до відстані від джерела звуку. Звуковий тиск р1 і р2 в крапках, розташованих від джерела на відстанях r1 або r2, зв'язаний співвідношенням р1/ р2= r2/ r1.
Для плоскої хвилі ні звуковий тиск, ні інтенсивність в якій-небудь крапці не залежать від положення крапки в просторі. Для плоскої хвилі існують наступні прості співвідношення між звуковим тиском р, коливальною швидкістю 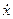і інтенсивністю I:
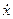= p/(ρc), I= 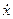ρc. (12.7)
де р і 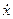можуть бути виражені або в амплітудних, або в діючих значеннях. Зв'язок між l і р така ж, як в сферичній хвилі.
Рис. 12.8 - Потік звукової енергії крізь поверхню
Ці співвідношення аналогічні закону Ома і залежності потужності від струму і напруги в електричному ланцюзі з активним опором.
На практиці при звуковому тиску 1 Па коливальна швидкість згідно (12.7) 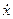=1/415=2,4∙10-3 м/с. Коливальний зсув на частотах 100, 1000 і 10 000 Гц згідно (2) відповідно рівно: х100=2,4∙10-3/(2∙π∙100)=3,8∙10-6 м, х1000=3,8∙10-7 м, х10000=3,8∙10-8 м. Амплітудні значення зсувів будуть в 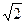більше. Прискорення на цих частотах згідно (2) 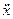100=2∙π∙100∙2,4∙10-3=1,5 м/с2, 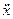1000=15 м/с2, 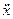10000=150 м/с2, тобто будуть задоволені великими.
Оскільки значення акустичних величин міняються в дуже широких межах, то їх зручно виражати не в абсолютних значеннях, а в логарифмічних. До того ж гучність звуку приблизно пропорційна логарифму акустичних величин (звукового тиску, інтенсивності і т. п.). Для обчислення таких логарифмічних значень (рівнів) користуються наступними залежностями:
Для звукового тиску: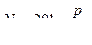 
.
Для інтенсивності: .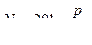
Величини N і М вимірюються в децибелах (дб). Як роо і Iоо зазвичай приймаються значення відповідно 2∙10-5 Па і 10-12 Вт/м2, рівень яких називається стандартним нульовим.
Покладемо, що слід визначити рівень звукового тиску 2 Па:
.
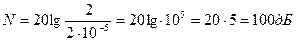Рівень звукового тиску в 1 Па буде рівний 94 дб.
Для створення звукового поля джерело звуку — випромінювач повинен розвивати деяку потужність, яку він випромінює. Очевидно, що для цього до джерела повинна бути підведена потужність. Припустимо, що джерело звуку є невагомий поршень, що коливається без тертя в нескінченній стіні. Якщо навколо поршня створений вакуум, то ясно, що для приведення поршня в коливання достатня нескінченно мала збудлива сила і відповідно така ж потужність. Проте картина різко зміниться, якщо поршень оточує звичайне середовище. Виявляється, що при цьому до поршня повинна бути прикладена певна збудлива сила F, що складається з активної і реактивної складових:
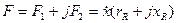. (12.8)
де 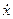- коливальна швидкість поршня.
Для того, щоб з'ясувати ролі величин rR і xR, помножимо обидві частини рівняння (12.8) на 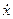. Очевидно, що в результаті множення сил на швидкість ми повинні отримати повну потужність в лівій частині і в правій частині — активну і реактивну її складові:
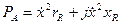. (12.9)
Отриманий вираз аналогічно виразу для повної електричної потужності в ланцюзі з індуктивністю і активним опором: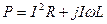 
.
У ідеальному випадку необмеженого середовища активна потужність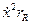 
йде на створення звукового поля в незбуджених частинах середовища. Вона втрачається поршнем необоротно і повинна безперервно поповнюватися. Формально, оскільки процес має необоротний характер, можна сказати, що потужність 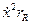витрачається на якомусь опорі 
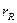. Опір 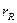називають опором випромінювання. Таким чином, що випромінює джерелом звуку потужність Р може бути виражена як:
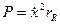. (12.10)
Зазвичай середовище, в якому відбувається розповсюдження звуку, обмежене (наприклад, поверхнями приміщення, межами земної атмосфери). Здавалося б що після збудження кінцевого об'єму середовища джерелу більше не на що витрачати свою потужність, але необхідно пам'ятати, що реальні середовища володіють поглинанням, тобто при розповсюдженні звуку частина його енергії перетворюється на тепло. Втрати потужності мають місце також при віддзеркаленні звуку від обмежуючих об'ємів звукопоглинальних поверхонь. Тому при розповсюдженні звуку в кінцевих об'ємах джерело повинне також доставляти потужність для покриття цих втрат.
Що стосується реактивної потужності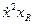 
, то справа йде так, як ніби із-за наявності середовища, що оточує поршень, поршень придбав якусь додаткову масу і відповідно механічний реактивний (інерційне) опір. Ця маса, що виявляється при коливаннях, обумовлена наявністю середовища, носить назву коливальної або приєднаної маси.
Величини rR і xR не є постійними, а залежать від виду джерела, його поверхні, від співвідношення між розмірами джерела і довжиною хвилі випромінюваного звуку, а також від питомого акустичного опору середовища.
Повний опір випромінювання zR може бути виражений як
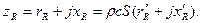(12.11)
де S - поверхня джерела;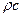 
- хвильовий або питомий акустичний опір середовища; 
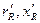- відповідно безрозмірні питомі коефіцієнти активного і реактивного опорів, віднесені до одиниці поверхні джерела і до середовища з одиничним питомим акустичним опором.
Значення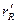 
і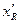 
можуть бути обчислені за допомогою задоволених складних математичних викладень. Результати цих обчислень для поршня, що коливається в нескінченній стіні (рис. 12.9, а), зображені графічно на рис. 12.10, а. Тут коефіцієнти 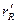і 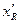виражені залежно від значення 
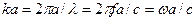, де а - радіус поршня.
При великих і малих значеннях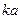 
, тобто відповідно на високих і низьких частотах, для коефіцієнтів 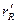і 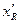виходять наступні наближені вирази: при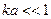 
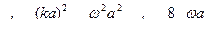. (12.12)
при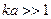 
.
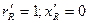Рис. 12.9 - Три типи поршневих випромінювачів:
а — круглий поршень в нескінченній стіні;
б — односторонній поршень без екрану;
в — двосторонній поршень без екрану
Коефіцієнт 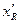визначає реактивну частину опору випромінювання на низьких частотах (при малих 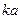). Повний опір цій частині:
.
Воно обумовлене деякій коливальній або приєднаною масою 
. Тому величину 
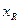іноді називають інерційною частиною опору випромінювання.
При коливаннях поршня не в нескінченній стіні можливі два випадки: одна поверхня закрита і не випромінює (рис. 12.9, 6), обидві поверхні поршня відкрито і випромінюють (рис. 12.9, в). У другому випадку при русі поршня, наприклад, управо, він створює згущування правою стороною і розрідження — лівою. Якщо узяти яку-небудь точку середовища, що знаходиться в площині поршня, то очевидно, що згущування і розрідження доходять до неї одночасно і нейтралізуються. Отже, в площині поршня звуковий тиск рівний нулю. Візьмемо тепер крапку О, лежачу де-небудь поза площиною поршня. Шляхи коливань (згущування і розрідження) до крапки О від обох сторін поршня розрізняються на якусь величину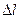 
. Відповідно різниця фаз φ коливань, що приходять від обох сторін поршня, рівна вже не 0, а 
.
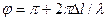Член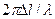 
повинен бути чималим, щоб в крапці О згущування розрідження не нейтралізувалися. На низьких частотах при заданій різниці шляхів 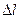значення 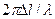мале. Тому буде мало і звуковий тиск, що розвивається. Щоб збільшити звуковий тиск на низьких частотах, необхідно поршень поміщати в нескінченну стіну (при цьому 
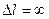), а практично - в екран достатньо великих розмірів.
Зазвичай замість екрану застосовують оформлення у вигляді відкритих із заднього боку ящиків, про що докладніше буде сказано далі.
У поршні із закритою задньою поверхнею, зображеному на рис. 12.9, 6, нейтралізація звукового тиску, що створюється передньою поверхнею поршня, відсутня. Проте на низьких частотах звуковий тиск, що створюється таким поршнем, менше, ніж звуковий тиск, що створюється поршнем, що коливається в нескінченній стіні. Це відбувається за рахунок того, що в першому випадку енергія випромінюється в навколишнє середовище в межах тілесного кута 4π,, тоді як в другому вона випромінюється тільки в межах кута 2π. На високих частотах різниця буде невеликою із-за спрямованості випромінювання,, про що буде сказано далі. Отже, для випромінювання звуків низьких частот важливо поміщати поршень у великий екран.
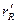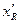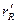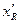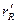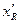На рис. 12.10 окрім кривих і для поршня в нескінченному екрані (а) приведені криві і для поршня, закритого з одного боку (б), і криві і для поршня, відкритого з двох сторін (в). Для малих значень 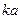аналогічно (12.12) значення 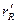відповідно рівні:
(12.13)
Відповідно значення 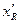будуть:
.
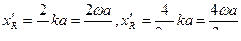Звідси можна отримати для величини коливальної маси:
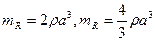. (12.14)
Рис. 12.10 - Питомий опір випромінювання різних видів випромінювачів
Опір випромінювання, будучи вельми малим для поршня, що малого в порівнянні з довжиною хвилі і коливається в нескінченному екрані, стає ще менше, якщо цей поршень коливається без екрану або випромінює тільки однією стороною. Таким чином, для випромінювання значних потужностей поршень, що малий в порівнянні з довжиною хвилі і має малий опір випромінювання, повинен мати вельми великі коливальні швидкості [див. (12.10)].
Розглянемо випромінювання поршня, що знаходиться в нескінченному екрані (рис. 12.11). Покладемо, що ми знаходимося в крапці, розташованій на прямою, що йде під кутом α до осі поршня. Якщо ця крапка розташована достатньо далеко від поршня, то можна вважати, що всі прямі, проведені від різних точок поверхні поршня до неї, йтимуть майже паралельно. Коливання ж, що розповсюджуються уздовж цих прямих, прийдуть в цю крапку з різними фазами. Звідси коливання від крайніх крапок поршня діаметром d прийдуть в дану крапку із зрушенням фази:
.
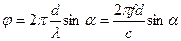При чималому відношенні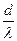 
коливання від різних крапок діафрагми приходитимуть у фазі або з невеликою різницею фаз тільки у напрямі осі або близькому до неї (α мало). Тому в цих напрямах матиме місце помітне випромінювання.
У інших напрямах різниці фаз коливань можуть бути такими, що вони будуть нейтралізуватися. Отже, в цих напрямах випромінювання буде мале або абсолютно відсутній. Таким чином, випромінювана звукова енергія концентрується в межах більш менш вузького тілесного кута.
Рис. 12.11 - Випромінювання поршня у різних напрямах щодо його осі
Рис. 12.12 - Характеристика спрямованості при відношенні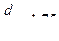 
Кількісно спрямованість випромінювання визначається характеристиками спрямованості, що зазвичай зображаються в полярних координатах.
Характеристика спрямованості є графічним зображенням відносної величини звукового тиску Rα, що розвивається випромінювачем в даному напрямі, в порівнянні з тиском, випромінювачем, що розвивається, у напрямі осі, залежно від кута, утвореного віссю випромінювача і напрямом випромінювання. Так, наприклад, змірявши на рис. 12.12 радіус-вектор, отримаємо, що звуковий тиск на будь-якій відстані від випромінювача під кутом 15° до його осі складає 0,8 значень звукового тиску на тій же відстані по осі випромінювача. При випромінюванні поршня без екрану характеристика спрямованості зображається косинусоїдою (вісімкою при побудові в полярних координатах).
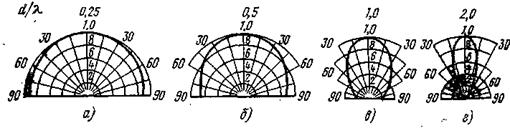
Рис. 12.13 - Характеристика спрямованості випромінювання поршня у
безкінечному екрані при різних відношеннях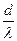
На рис. 12.13 зображені характеристики спрямованості випромінювання поршня, поміщеного в нескінченний екран для різних значень відношення діаметру поршня до довжини хвилі. Спрямованість випромінювача може бути оцінена і через так званий коефіцієнт концентрації - відношення потужності, що випромінює направленим випромінювачем, що розвиває звуковий тиск, таке ж, як і у ненаправленого випромінювача на його осі до потужності, що випромінює останнім. Коефіцієнт концентрації для ненаправленого випромінювача рівний одиниці, а для випромінювача з восьмирічною (косинусоїдальною) характеристикою спрямованості — трьом. Спрямованість реальних випромінювачів в залежності від частоти описується складнішим чином і практично визначається при вимірюваннях.
Дата: 2019-03-05, просмотров: 270.
