ОПРЕДЕЛЕНИЕ РАБОТЫ АДГЕЗИИ
К ПОВЕРХНОСТИ ТВЕРДЫХ ТЕЛ
Методические указания
к лабораторной работе
Казань 2001
Составители: доц. Е.Г.Белов,
проф. А.М.Коробков,
доц. Т.В.Бурдикова,
ст. преп. Л.И.Кельдышева
Определение работы адгезии к поверхности твердых тел: Метод. указания к лабораторной работе / Сост.: Е.Г. Белов и др. Казан. гос. технол. ун-т. Казань, 2001. 16 с.
Рассмотрены вопросы смачивания жидкостями поверхности твердых тел. Изложены теоретические основы смачивания, методы определения величин, характеризующих это явление, процессы, в основе которых лежит смачивание.
Предназначены для студентов, обучающихся по специальностям 121000 и 251400, изучающих курсы “Физико-химия твердого состояния, поверхностных и контактных явлений”, ”Физика и механика композиционных материалов”, “Материаловедение”, а также научных сотрудников и аспирантов, занимающихся исследованиями в области фильтрации, смазок, пропитки, гетерогенного взаимодействия и др.
Подготовлены на кафедре химии и технологии гетерогенных систем.
Печатаются по решению методической комиссии инженерного химико-технологического факультета.
Рецензенты: доц. Ю.М. Филиппов,
доц. Н.С. Хайруллина
Введение
Явления, протекающие на поверхности раздела фаз, имеют огромное практическое значение. Это, в частности, касается таких областей, как конструирование, производство и эксплуатация композиционных материалов (КМ). Если рассматривать принципы классификации КМ по методам их получения, то видно, что каждый метод базируется на физико-химической природе одного или нескольких поверхностных явлений (ПЯ). Например, получение КМ жидкофазными методами (пропитка, направленная кристаллизация и др.) основано на таких ПЯ, как капиллярные явления, смачивание, адгезия, образование новой фазы, растворение.
Практически все методы получения КМ сопровождаются межфазным взаимодействием. Смачивание - одна из важнейших характеристик межфазного взаимодействия в КМ, которую необходимо учитывать при планировании получения КМ жидкофазными методами. Так, получение КМ методом пропитки и обеспечение прочной связи между компонентами, в частности за счет адгезии, возможно только при условии, что жидкая матрица смачивает поверхность армирующих элементов. Смачивание - это процесс самопроизвольного уменьшения свободной энергии системы, состоящей из трех фаз, и сопровождающийся поверхностной диффузией молекул.
Теоретическая часть
Поверхностное натяжение
Поверхностная энергия играет исключительно важную роль в большом числе самых разнообразных явлений. Свойства поверхности раздела фаз сказываются прежде всего на испарении, сублимации и конденсации, так как при переходе вещества из одной фазы в другую его молекулы должны пройти через эти поверхности. В таких процессах, как адсорбция, диффузия, катализ, химические реакции в гетерогенных системах, вещество либо проходит через поверхностный слой, либо поглощается им, либо вытесняется из него в объем. Трение, смазочное действие и адгезия также связаны с поверхностными свойствами веществ.
Молекулы в поверхностном слое по своему энергетическому состоянию отличаются от молекул в объеме. Молекула в объеме испытывает в среднем одинаковое притяжение окружающих ее молекул, вследствие чего равнодействующая молекулярных сил в объеме равна нулю. В отношении молекул, находящихся на поверхности раздела фаз, равнодействующая молекулярных сил притяжения не равна нулю и направлена внутрь объема фазы нормально к ее поверхности.
Диспергирование твердых тел приводит к образованию новой поверхности раздела, т.е. при диспергировании производится работа, направленная против действия молекулярных сил. В результате возникает свободная поверхностная энергия F св:
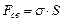 , (1)
, (1)
где s - свободная энергия единицы поверхности раздела; S - площадь поверхности раздела.
Свободная поверхностная энергия представляет собой избыток энергии реальной системы по сравнению с идеальной, в которой плотность свободной энергии остается неизменной вплоть до геометрической границы, разделяющей объемные фазы.
Величина s носит название поверхностного натяжения (ПН). Поверхностное натяжение может быть выражено либо в единицах силы на единицу длины, либо величиной энергии, приходящейся на единицу площади (в системе СИ ПН выражено единицей Н/м или Дж/м2, в системе СГС - эрг/см2 ).
При изотермическом и обратимом процессах образования 1 см2 поверхности свободная поверхностная энергия системы увеличивается на величину s, и прирост поверхностной энергии D F составит:
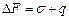 , (2)
, (2)
где q – тепло, поглощенное в процессе образования поверхности.
Поверхностное натяжение с ростом температуры уменьшается, поэтому
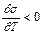 . (3)
. (3)
Условие равновесия трех фаз
Условия равновесия капли жидкости при смачивании ею твердой поверхности сформулированы Юнгом.
Рассмотрим равновесие трех любых фаз, имеющих произвольную форму. Предполагается, что смачивание происходит на границе трех фаз: твердое тело (т), жидкость (ж) и газ (г) (рис. 1).
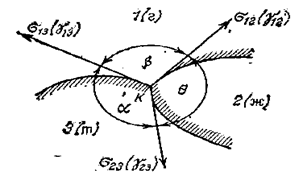
Рис. 1. Равновесие трехфазной системы
Касательные, проведенные к поверхности из точки касания, показывают направление и величину поверхностного натяжения. В условиях равновесия можно провести сложение векторов, соответствующих направлению, например s 32 ( g 32 ), тогда
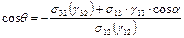 . (5)
. (5)
Через s обозначено поверхностное натяжение конденсированной фазы с газом, через g - поверхностное натяжение разнородных конденсированных фаз. Пусть фаза 1 – газ, фаза 2 – жидкость, фаза 3 – твердое тело, в этом случае
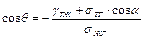 , (6)
, (6)
Если угол a=180° (cos a= -1), то
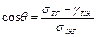 , (7)
, (7)
или
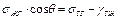 , (8)
, (8)
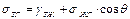 , (9)
, (9)
По периметру смачивания будут действовать три поверхностных натяжения (рис. 2).
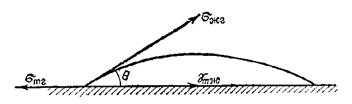
Рис. 2. Капля жидкости на поверхности твердого тела
Поверхностное натяжение на границе раздела твердое тело–газ sтг увеличивает площадь соприкосновения жидкости с твердой поверхностью и способствует растеканию капли. В противоположность этому поверхностное натяжение gтж препятствует растеканию капли и стремится сократить границу раздела жидкость-твердое тело. Поверхностное натяжение на границе жидкости с газом sжг стремится уменьшить поверхность капли, оно направлено под углом q к твердому телу.
Уравнения Юнга (5-9) являются фундаментальными уравнениями, связывающими поверхностное натяжение с углом q.
Краевой угол смачивания
Угол q - краевой угол смачивания (КУС) является одной из основных характеристик смачивания. Краевой угол смачивания равен углу между направлениями векторов поверхностных натяжений sжг и gтж. Значения q и sжг определяются экспериментально. Значения sжг для некоторых жидкостей приведены в работе [1]. Краевой угол является мерой смачивания поверхностей. Если q<900, твердые поверхности хорошо смачиваются жидкостью, такие поверхности называются олеофильными. Если q>900, происходит ограниченное смачивание поверхностей, которые называются олеофобными. При смачивании поверхностей водой используют понятия “гидрофильность” и “гидрофобность”. Теоретически, когда q=00 и q=1800 существуют понятия абсолютного смачивания и абсолютного несмачивания. Условно при q=00 поверхностное натяжение sжг называется критическим и обозначается sс.
Значение КУС (q ) зависит от многих факторов - природы твердой поверхности и жидкости, температуры, наличия примесей на поверхности твердого тела, наличия взаимодействия между жидкостью и твердой поверхностью.
В связи с тем, что КУС может измениться для одной и той же системы в зависимости от различных условий, более объективно о смачивании поверхности можно судит по величине sтг. В этом случае различают низкоэнергетические и высокоэнергетические поверхности. Низкоэнергетические поверхности смачиваются не полностью и реализуют определенный угол. К таким поверхностям относятся твердые полимеры и органические соединения (sтг в пределах 15¸70 эрг/см2). Высокоэнергетические поверхности характеризуются относительно высокими значениями поверхностного натяжения (sтг в пределах 100¸500 эрг/см2) и sтг >> sжг. Отсюда имеет место полное растекание жидкости по твердой поверхности, отсутствует sс и зависимость 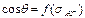 . К таким твердым телам относятся металлы, их оксиды, стекло, рубин, кварц, алмаз и др.
. К таким твердым телам относятся металлы, их оксиды, стекло, рубин, кварц, алмаз и др.
Работа адгезии
В первом приближении значение КУС может характеризовать адгезионное взаимодействие жидкости с поверхностью твердого тела. Для такой же оценки используют произведение 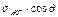 , которое называется энергией смачивания (равная проекции sжг):
, которое называется энергией смачивания (равная проекции sжг):
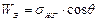 . (10)
. (10)
Энергия смачивания W Э характеризует направление sтг и gтж. Однако чаще взаимодействие двух фаз (например, жидкости с твердой поверхностью) характеризуется работой адгезии. В данном случае работа адгезии (W А) определяется, как разность между ( 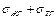 ) и поверхностным натяжением gтж по закону Дюпре:
) и поверхностным натяжением gтж по закону Дюпре:
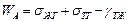 . (11)
. (11)
Смысл этого уравнения легко пояснить с помощью рис. 3.
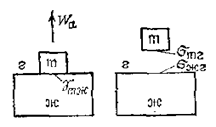
Рис. 3. Схема, поясняющая работу адгезии и когезии
Работа адгезии определяется той работой, которую необходимо затратить для удаления жидкости с поверхности твердого тела. При контакте с твердой поверхностью свободная поверхностная энергия равна gтж, а после разъединения твердого тела и жидкости она становится равной ( 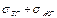 ). С учетом уравнения (9) работа адгезии равна:
). С учетом уравнения (9) работа адгезии равна:
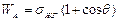 , (12)
, (12)
где величины sжг и q могут быть легко определены экспериментально.
Часто работу адгезии сопоставляют с работой когезии. Работа когезии равна той работе, которую надо приложить, чтобы преодолеть взаимодействие между собой молекул жидкости. При этом образуются две поверхности раздела фаз жидкость-газ. Работа когезии равна удвоенному значению свободной поверхностной энергии (поверхностного натяжения) образовавшихся фаз, т.е.
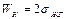 . (13)
. (13)
Связь между адгезией и когезией можно выразить посредством параметра Ф. В основу этой связи положены неформальные соотношения между работами адгезии и когезии, а соотношения в величинах дисперсионного взаимодействия. Соотношение работ адгезии и когезии двух фаз (например, твердое тело-жидкость) можно представить в виде уравнения:
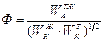 , (14)
, (14)
где 
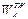 - работа адгезии жидкости к твердому телу;
- работа адгезии жидкости к твердому телу; 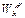 - работа когезии жидкости;
- работа когезии жидкости; 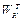 - работа когезии твердого тела.
- работа когезии твердого тела. 
Параметр Ф связан с поверхностным натяжением контактирующих фаз:
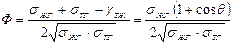 . (15)
. (15)
Параметр Ф можно определить экспериментально. В свою очередь, знание этого параметра дает возможность определить такую важную величину, как поверхностное натяжение твердого тела:
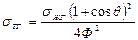 (16)
(16)
или значение краевых углов:
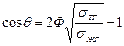 . (17)
. (17)
Другой метод определения Ф основан на учете молекулярного взаимодействия двух фаз:
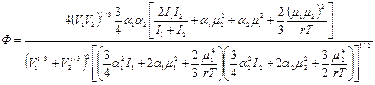 , (18)
, (18)
где V 1, V 2 - мольные объемы контактирующих фаз; a - поляризуемость; m - дипольный момент; I - энергия ионизации; r - константа Больцмана; T – температура.
Для низкоэнергетических поверхностей (sтг=5¸44 эрг/см2) установлена зависимость:
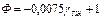 . (19)
. (19)
Используя уравнение Юнга, можно получить выражение:
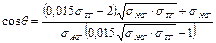 . (20)
. (20)
В этом случае поверхностное натяжение вычисляется с использованием итерационных методов математического программирования.
Смачивание шероховатых поверхностей по сравнению с гладкими имеет ряд особенностей. Эти особенности проявляются в изменении на шероховатых поверхностях основных показателей, характеризующих адгезию и смачивание, к числу которых относятся краевой угол, работа адгезии и критическое поверхностное натяжение. Причина изменения этих показателей кроется либо в увеличении их за счет неровностей фактической площади контакта жидкости с твердым телом, либо за счет изменения дисперсионной составляющей взаимодействия из-за наличия на твердой поверхности адсорбционных слоев другого вещества.
Увеличение площади фактического контакта приводит к пропорциональному росту удельной свободной поверхностной энергии. Таким образом, поверхностное натяжение шероховатой и гладкой поверхностей связаны между собой соотношениями:
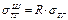 ;
; 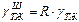 (21)
(21)
Помимо фактической различают еще номинальную площадь контакта, которая равна площади проекции на гладкую поверхность, т.е. 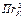 (r к - радиус контакта). Отсюда R - это отношение фактической площади контакта жидкости к номинальной площади контакта. Условия равновесия в этом случае следующие:
(r к - радиус контакта). Отсюда R - это отношение фактической площади контакта жидкости к номинальной площади контакта. Условия равновесия в этом случае следующие:
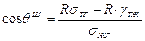 , (22)
, (22)
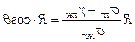 , (23)
, (23)
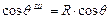 . (24)
. (24)
Уравнение (24) было экспериментально получено Р. Венцелем и теоретически обосновано Б.В.Дерягиным, оно получило название уравнение Венцеля-Дерягина. Вследствие того, что R всегда больше 1, для гидрофильной поверхности при cos q >0
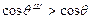 , а
, а 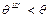 ;
;
а для гидрофобной поверхности при cos q <0
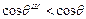 , а
, а 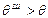 .
.
Таким образом, наличие шероховатостей ухудшает смачивание гидрофобных поверхностей и улучшает смачивание гидрофильных поверхностей. В первом случае жидкость не способна проникнуть в углубление шероховатой поверхности, во-втором - жидкость легко проникает в углубление шероховатой поверхности.
Работу адгезии с учетом формулы (21) можно представить в виде:
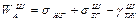 (25)
(25)
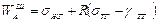
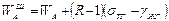 (26)
(26)
Следовательно, работа адгезии на шероховатых поверхностях всегда больше работы адгезии на гладкой поверхности в расчете на единицу поверхности.
Поверхность порошкообразных и пористых тел в первом приближении можно принять за шероховатую поверхность твердых тел. Однако порошкообразные и пористые тела являются капиллярными системами и процесс смачивания будет сопровождаться впитыванием жидкости. Смачивание порошков и пористых тел можно определить по величине краевого угла. В данном случае краевой угол может быть рассчитан по следующим формулам:
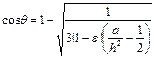 , (28)
, (28)
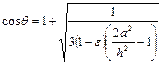 , (29)
, (29)
где e - пористость системы; а - капиллярная постоянная; h - высота капли.
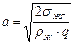 ,
,
где r ж - плотность жидкости.
Пористость системы можно связать с радиусом пор системы следующей формулой:
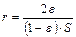 ,
,
где S - удельная поверхность частицы.
Согласно теоретическим представлениям Б.В.Дерягина краевой угол при смачивании пористой поверхности можно оценить по выражению
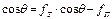 , (30)
, (30)
где f Т и f П - доля поверхности, занятой сплошным твердым телом и порами.
В реальных условиях поверхность твердых тел не является физически и химически чистой. Наличие на поверхности адсорбированных слоев другого вещества, образованных гетерогенным путем или в результате модификации поверхности, приводит к изменению поверхностного натяжения sтг и краевого угла q, что сказывается на работе адгезии. Реальная работа адгезии с учетом адсорбции на твердой поверхности равна:
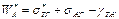 (31)
(31)
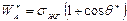 (32)
(32)
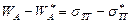 (33)
(33)
Реальная работа адгезии отличается от работы адгезии при участии чистой поверхности на величину 
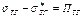 , где
, где 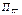 - величина, учитывающая изменение sтг в результате адсорбции.
- величина, учитывающая изменение sтг в результате адсорбции.
Таким образом, смачивание и адгезию можно целенаправленно изменить в желаемом направлении.
2. Методы определения краевого угла смачивания
Адгезия жидкости и ее способность смачивать твердые поверхности характеризуются краевым углом смачивания и работой адгезии. Эти два параметра поддаются измерению. Можно перечислить следующие методы определения КУС:
Прямые измерения краевого угла.
Расчет краевого угла по форме капли.
Определение краевого угла методом погружения.
Лабораторная работа
Цель работы. Определить краевой угол смачивания жидкости на поверхности твердых тел. Вычислить работу адгезии. Оценить поверхностную энергию твердого тела.
Приборы и реактивы: проекционный фонарь, экран с транспортиром, микропипетки, набор жидкостей, набор пластин.
Сущность работы. Работу адгезии определяют по формуле (12), если известны поверхностное натяжение на границе с воздухом и краевой угол смачивания жидкостью поверхности твердого тела. Из формулы (20) можно определить поверхностное натяжение (свободную поверхностную энергию) твердого тела. В данной работе определяют адгезию жидкости на твердой пластине и оценивают поверхностное натяжение твердого тела. Для решения этого вопроса необходимо измерить краевой угол смачивания твердой пластины жидкостью.
Порядок выполнения работы
В последнее время разработано много методов определения краевого угла смачивания [1]. Однако наиболее надежным и доступным является метод непосредственного измерения краевого угла между поверхностью капли, находящейся на пластине, и поверхностью пластины. Каплю проецируют на экран (см. рис. 3), добиваясь максимальной резкости в изображении контура капли. На проекции капли проводят касательную в точке пересечения контура капли с подложкой и измеряют угол наклона этой касательной (см. рис. 4). Возможная ошибка измерения краевого угла может составлять 3-5 0.
Небольшую пластину тщательно обезжиривают, промывают хромовой смесью, серным эфиром и дистиллированной водой. После такой подготовки пластину берут только за края, ни в коем случае не прикасаясь пальцами к ее поверхности, и помещают в фокус объектива проектора. Затем с помощью бюретки (пипетки) на поверхность пластины помещают каплю жидкости. После получения резкого изображения капли на экране проводят замер краевого угла смачивания. Процедуру нанесения капли и замера угла проводят несколько раз. По результатам измерений вычисляют среднее значение угла, дисперсию и доверительный интервал. Поверхностные натяжения на границе с воздухом некоторых жидкостей при различной температуре приведены в работе [1].
По полученному среднему значению краевого угла находят cos q. Работу адгезии и поверхностное натяжение твердого тела вычисляют по формулам (12,16-20), подставляя в них поверхностное натяжение жидкости при фиксированной температуре и значении cos q . Полученные данные сводят в табл. 1, описывают, анализируют, делают выводы.
Таблица 1
| Условия эксперимента | Результаты измерений | |||||
| Природа твердой поверхности | Природа жидкости | темпера- тура Т , К | состояние поверх- ности | краевой угол смачивания
q, град. 
| cos q | поверхностное натяжение s жт, Дж/м2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Результаты вычислений записывают в табл. 2.
Таблица 2
| Результаты вычислений | |||
| Природа твердой поверхности | Природа жидкости | работа адгезии W, Дж | поверхностное натяжение твердого тела s тг, Дж/см2 |
| 1 | 2 | 3 | 4 |
Все результаты измерений и вычислений записываются в системе СИ.
Библиографический список
1. Зимон А.Д. Адгезия жидкости и смачивание. М.: Химия, 1974. – 416 с.
2. Хинней Н. Химия твёрдого тела: Пер. с англ. /Под ред. В.В. Болдырева. М.: Мир, 1971. – 223 с.
3. Адамсон А. Физическая химия поверхностей: Пер с англ. /Под ред. Б.В. Дерягина. М.: Мир, 1979. – 568 с.
Приложение
Коэффициенты Стьюдента
| Число опытов | a=0,90 | a=0,95 |
| 1 2 3 4 5 6 7 8 9 | 6,31 2,92 2,35 2,13 2,02 1,95 1,89 1,86 1,83 | 12,7 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 |
Таблица 3
Поверхностное натяжение на границе с воздухом некоторых жидкостей
при различной температуре
| Жидкость | Темпера-тура, 0С | s, эрг/см2 | Жидкость | Темпера-тура, 0С | s, эрг/см2 |
| Вода | -10 -5 0 5 10 15 18 20 25 30 35 40 45 50 60 70 80 90 100 | 77,10* 76,40* 75,62 74,90 74,20 73,48 73,05 72,75 71,96 71,15 70,35 69,55 68,73 67,90 67,17 64,41 62,60 60,74 54,84 | Бензол Четыреххлористый углерод Этиловый спирт Пропиловый спирт Изопропиловый спирт Этиленгликоль Глицерин Ацетон Уксусная кислота Этилацетат Анилин | 20 30 20 20 40 60 25 18 20 20 20 20 30 20 30 20 | 28,87 27,50 25,68 22,03 20,20 18,43 22,9 21,2 46,11 62,47 23,7 27,79 26,87 23,75 22,25 43,66 |
Примечание: 1 эрг=1×10-7 Дж, 1см=1×10-2 м, * - для переохлажденной жидкости.
Редактор Н.В.Лабзова
Лицензия № 020404 от 6.03.97г.
Подписано в печать Формат 60´84 1/16
Бумага писчая. Печать Riso 0,93 усл. печ. л.
1,0 уч.-изд. л. Тираж экз. Заказ “С”
Издательство Казанского государственного
технологического университета
ОПРЕДЕЛЕНИЕ РАБОТЫ АДГЕЗИИ
К ПОВЕРХНОСТИ ТВЕРДЫХ ТЕЛ
Методические указания
к лабораторной работе
Казань 2001
Составители: доц. Е.Г.Белов,
проф. А.М.Коробков,
доц. Т.В.Бурдикова,
ст. преп. Л.И.Кельдышева
Определение работы адгезии к поверхности твердых тел: Метод. указания к лабораторной работе / Сост.: Е.Г. Белов и др. Казан. гос. технол. ун-т. Казань, 2001. 16 с.
Рассмотрены вопросы смачивания жидкостями поверхности твердых тел. Изложены теоретические основы смачивания, методы определения величин, характеризующих это явление, процессы, в основе которых лежит смачивание.
Предназначены для студентов, обучающихся по специальностям 121000 и 251400, изучающих курсы “Физико-химия твердого состояния, поверхностных и контактных явлений”, ”Физика и механика композиционных материалов”, “Материаловедение”, а также научных сотрудников и аспирантов, занимающихся исследованиями в области фильтрации, смазок, пропитки, гетерогенного взаимодействия и др.
Подготовлены на кафедре химии и технологии гетерогенных систем.
Печатаются по решению методической комиссии инженерного химико-технологического факультета.
Рецензенты: доц. Ю.М. Филиппов,
доц. Н.С. Хайруллина
Введение
Явления, протекающие на поверхности раздела фаз, имеют огромное практическое значение. Это, в частности, касается таких областей, как конструирование, производство и эксплуатация композиционных материалов (КМ). Если рассматривать принципы классификации КМ по методам их получения, то видно, что каждый метод базируется на физико-химической природе одного или нескольких поверхностных явлений (ПЯ). Например, получение КМ жидкофазными методами (пропитка, направленная кристаллизация и др.) основано на таких ПЯ, как капиллярные явления, смачивание, адгезия, образование новой фазы, растворение.
Практически все методы получения КМ сопровождаются межфазным взаимодействием. Смачивание - одна из важнейших характеристик межфазного взаимодействия в КМ, которую необходимо учитывать при планировании получения КМ жидкофазными методами. Так, получение КМ методом пропитки и обеспечение прочной связи между компонентами, в частности за счет адгезии, возможно только при условии, что жидкая матрица смачивает поверхность армирующих элементов. Смачивание - это процесс самопроизвольного уменьшения свободной энергии системы, состоящей из трех фаз, и сопровождающийся поверхностной диффузией молекул.
Теоретическая часть
Поверхностное натяжение
Поверхностная энергия играет исключительно важную роль в большом числе самых разнообразных явлений. Свойства поверхности раздела фаз сказываются прежде всего на испарении, сублимации и конденсации, так как при переходе вещества из одной фазы в другую его молекулы должны пройти через эти поверхности. В таких процессах, как адсорбция, диффузия, катализ, химические реакции в гетерогенных системах, вещество либо проходит через поверхностный слой, либо поглощается им, либо вытесняется из него в объем. Трение, смазочное действие и адгезия также связаны с поверхностными свойствами веществ.
Молекулы в поверхностном слое по своему энергетическому состоянию отличаются от молекул в объеме. Молекула в объеме испытывает в среднем одинаковое притяжение окружающих ее молекул, вследствие чего равнодействующая молекулярных сил в объеме равна нулю. В отношении молекул, находящихся на поверхности раздела фаз, равнодействующая молекулярных сил притяжения не равна нулю и направлена внутрь объема фазы нормально к ее поверхности.
Диспергирование твердых тел приводит к образованию новой поверхности раздела, т.е. при диспергировании производится работа, направленная против действия молекулярных сил. В результате возникает свободная поверхностная энергия F св:
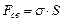 , (1)
, (1)
где s - свободная энергия единицы поверхности раздела; S - площадь поверхности раздела.
Свободная поверхностная энергия представляет собой избыток энергии реальной системы по сравнению с идеальной, в которой плотность свободной энергии остается неизменной вплоть до геометрической границы, разделяющей объемные фазы.
Величина s носит название поверхностного натяжения (ПН). Поверхностное натяжение может быть выражено либо в единицах силы на единицу длины, либо величиной энергии, приходящейся на единицу площади (в системе СИ ПН выражено единицей Н/м или Дж/м2, в системе СГС - эрг/см2 ).
При изотермическом и обратимом процессах образования 1 см2 поверхности свободная поверхностная энергия системы увеличивается на величину s, и прирост поверхностной энергии D F составит:
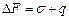 , (2)
, (2)
где q – тепло, поглощенное в процессе образования поверхности.
Поверхностное натяжение с ростом температуры уменьшается, поэтому
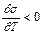 . (3)
. (3)
Применяя уравнение Гиббса-Гельмгольца к поверхности раздела, получим
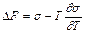 . (4)
. (4)
Уравнение показывает, что полная поверхностная энергия D F единицы поверхности больше ее свободной энергии s и слагается из двух величин: s и 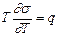 , т.е. для определения D F по уравнению необходимо измерить поверхностное натяжение s и знать температурный коэффициент ¶s/¶T.
, т.е. для определения D F по уравнению необходимо измерить поверхностное натяжение s и знать температурный коэффициент ¶s/¶T.
Условие равновесия трех фаз
Условия равновесия капли жидкости при смачивании ею твердой поверхности сформулированы Юнгом.
Рассмотрим равновесие трех любых фаз, имеющих произвольную форму. Предполагается, что смачивание происходит на границе трех фаз: твердое тело (т), жидкость (ж) и газ (г) (рис. 1).

Рис. 1. Равновесие трехфазной системы
Касательные, проведенные к поверхности из точки касания, показывают направление и величину поверхностного натяжения. В условиях равновесия можно провести сложение векторов, соответствующих направлению, например s 32 ( g 32 ), тогда
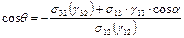 . (5)
. (5)
Через s обозначено поверхностное натяжение конденсированной фазы с газом, через g - поверхностное натяжение разнородных конденсированных фаз. Пусть фаза 1 – газ, фаза 2 – жидкость, фаза 3 – твердое тело, в этом случае
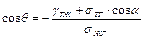 , (6)
, (6)
Если угол a=180° (cos a= -1), то
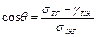 , (7)
, (7)
или
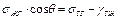 , (8)
, (8)
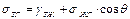 , (9)
, (9)
По периметру смачивания будут действовать три поверхностных натяжения (рис. 2).

Рис. 2. Капля жидкости на поверхности твердого тела
Поверхностное натяжение на границе раздела твердое тело–газ sтг увеличивает площадь соприкосновения жидкости с твердой поверхностью и способствует растеканию капли. В противоположность этому поверхностное натяжение gтж препятствует растеканию капли и стремится сократить границу раздела жидкость-твердое тело. Поверхностное натяжение на границе жидкости с газом sжг стремится уменьшить поверхность капли, оно направлено под углом q к твердому телу.
Уравнения Юнга (5-9) являются фундаментальными уравнениями, связывающими поверхностное натяжение с углом q.
Краевой угол смачивания
Угол q - краевой угол смачивания (КУС) является одной из основных характеристик смачивания. Краевой угол смачивания равен углу между направлениями векторов поверхностных натяжений sжг и gтж. Значения q и sжг определяются экспериментально. Значения sжг для некоторых жидкостей приведены в работе [1]. Краевой угол является мерой смачивания поверхностей. Если q<900, твердые поверхности хорошо смачиваются жидкостью, такие поверхности называются олеофильными. Если q>900, происходит ограниченное смачивание поверхностей, которые называются олеофобными. При смачивании поверхностей водой используют понятия “гидрофильность” и “гидрофобность”. Теоретически, когда q=00 и q=1800 существуют понятия абсолютного смачивания и абсолютного несмачивания. Условно при q=00 поверхностное натяжение sжг называется критическим и обозначается sс.
Значение КУС (q ) зависит от многих факторов - природы твердой поверхности и жидкости, температуры, наличия примесей на поверхности твердого тела, наличия взаимодействия между жидкостью и твердой поверхностью.
В связи с тем, что КУС может измениться для одной и той же системы в зависимости от различных условий, более объективно о смачивании поверхности можно судит по величине sтг. В этом случае различают низкоэнергетические и высокоэнергетические поверхности. Низкоэнергетические поверхности смачиваются не полностью и реализуют определенный угол. К таким поверхностям относятся твердые полимеры и органические соединения (sтг в пределах 15¸70 эрг/см2). Высокоэнергетические поверхности характеризуются относительно высокими значениями поверхностного натяжения (sтг в пределах 100¸500 эрг/см2) и sтг >> sжг. Отсюда имеет место полное растекание жидкости по твердой поверхности, отсутствует sс и зависимость 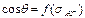 . К таким твердым телам относятся металлы, их оксиды, стекло, рубин, кварц, алмаз и др.
. К таким твердым телам относятся металлы, их оксиды, стекло, рубин, кварц, алмаз и др.
Работа адгезии
В первом приближении значение КУС может характеризовать адгезионное взаимодействие жидкости с поверхностью твердого тела. Для такой же оценки используют произведение 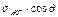 , которое называется энергией смачивания (равная проекции sжг):
, которое называется энергией смачивания (равная проекции sжг):
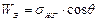 . (10)
. (10)
Энергия смачивания W Э характеризует направление sтг и gтж. Однако чаще взаимодействие двух фаз (например, жидкости с твердой поверхностью) характеризуется работой адгезии. В данном случае работа адгезии (W А) определяется, как разность между ( 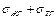 ) и поверхностным натяжением gтж по закону Дюпре:
) и поверхностным натяжением gтж по закону Дюпре:
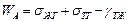 . (11)
. (11)
Смысл этого уравнения легко пояснить с помощью рис. 3.

Рис. 3. Схема, поясняющая работу адгезии и когезии
Работа адгезии определяется той работой, которую необходимо затратить для удаления жидкости с поверхности твердого тела. При контакте с твердой поверхностью свободная поверхностная энергия равна gтж, а после разъединения твердого тела и жидкости она становится равной ( 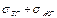 ). С учетом уравнения (9) работа адгезии равна:
). С учетом уравнения (9) работа адгезии равна:
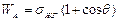 , (12)
, (12)
где величины sжг и q могут быть легко определены экспериментально.
Часто работу адгезии сопоставляют с работой когезии. Работа когезии равна той работе, которую надо приложить, чтобы преодолеть взаимодействие между собой молекул жидкости. При этом образуются две поверхности раздела фаз жидкость-газ. Работа когезии равна удвоенному значению свободной поверхностной энергии (поверхностного натяжения) образовавшихся фаз, т.е.
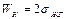 . (13)
. (13)
Связь между адгезией и когезией можно выразить посредством параметра Ф. В основу этой связи положены неформальные соотношения между работами адгезии и когезии, а соотношения в величинах дисперсионного взаимодействия. Соотношение работ адгезии и когезии двух фаз (например, твердое тело-жидкость) можно представить в виде уравнения:
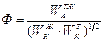 , (14)
, (14)
где 
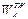 - работа адгезии жидкости к твердому телу;
- работа адгезии жидкости к твердому телу; 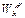 - работа когезии жидкости;
- работа когезии жидкости; 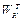 - работа когезии твердого тела.
- работа когезии твердого тела. 
Параметр Ф связан с поверхностным натяжением контактирующих фаз:
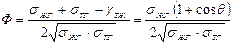 . (15)
. (15)
Параметр Ф можно определить экспериментально. В свою очередь, знание этого параметра дает возможность определить такую важную величину, как поверхностное натяжение твердого тела:
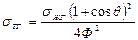 (16)
(16)
или значение краевых углов:
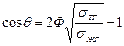 . (17)
. (17)
Другой метод определения Ф основан на учете молекулярного взаимодействия двух фаз:
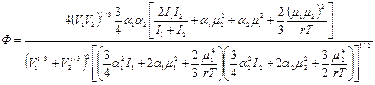 , (18)
, (18)
где V 1, V 2 - мольные объемы контактирующих фаз; a - поляризуемость; m - дипольный момент; I - энергия ионизации; r - константа Больцмана; T – температура.
Для низкоэнергетических поверхностей (sтг=5¸44 эрг/см2) установлена зависимость:
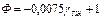 . (19)
. (19)
Используя уравнение Юнга, можно получить выражение:
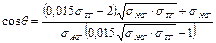 . (20)
. (20)
В этом случае поверхностное натяжение вычисляется с использованием итерационных методов математического программирования.
Смачивание шероховатых поверхностей по сравнению с гладкими имеет ряд особенностей. Эти особенности проявляются в изменении на шероховатых поверхностях основных показателей, характеризующих адгезию и смачивание, к числу которых относятся краевой угол, работа адгезии и критическое поверхностное натяжение. Причина изменения этих показателей кроется либо в увеличении их за счет неровностей фактической площади контакта жидкости с твердым телом, либо за счет изменения дисперсионной составляющей взаимодействия из-за наличия на твердой поверхности адсорбционных слоев другого вещества.
Увеличение площади фактического контакта приводит к пропорциональному росту удельной свободной поверхностной энергии. Таким образом, поверхностное натяжение шероховатой и гладкой поверхностей связаны между собой соотношениями:
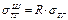 ;
; 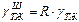 (21)
(21)
Помимо фактической различают еще номинальную площадь контакта, которая равна площади проекции на гладкую поверхность, т.е. 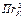 (r к - радиус контакта). Отсюда R - это отношение фактической площади контакта жидкости к номинальной площади контакта. Условия равновесия в этом случае следующие:
(r к - радиус контакта). Отсюда R - это отношение фактической площади контакта жидкости к номинальной площади контакта. Условия равновесия в этом случае следующие:
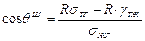 , (22)
, (22)
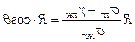 , (23)
, (23)
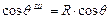 . (24)
. (24)
Уравнение (24) было экспериментально получено Р. Венцелем и теоретически обосновано Б.В.Дерягиным, оно получило название уравнение Венцеля-Дерягина. Вследствие того, что R всегда больше 1, для гидрофильной поверхности при cos q >0
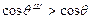 , а
, а 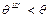 ;
;
а для гидрофобной поверхности при cos q <0
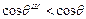 , а
, а 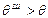 .
.
Таким образом, наличие шероховатостей ухудшает смачивание гидрофобных поверхностей и улучшает смачивание гидрофильных поверхностей. В первом случае жидкость не способна проникнуть в углубление шероховатой поверхности, во-втором - жидкость легко проникает в углубление шероховатой поверхности.
Работу адгезии с учетом формулы (21) можно представить в виде:
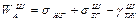 (25)
(25)
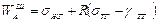
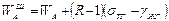 (26)
(26)
Следовательно, работа адгезии на шероховатых поверхностях всегда больше работы адгезии на гладкой поверхности в расчете на единицу поверхности.
Поверхность порошкообразных и пористых тел в первом приближении можно принять за шероховатую поверхность твердых тел. Однако порошкообразные и пористые тела являются капиллярными системами и процесс смачивания будет сопровождаться впитыванием жидкости. Смачивание порошков и пористых тел можно определить по величине краевого угла. В данном случае краевой угол может быть рассчитан по следующим формулам:
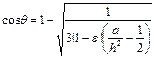 , (28)
, (28)
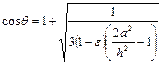 , (29)
, (29)
где e - пористость системы; а - капиллярная постоянная; h - высота капли.
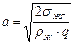 ,
,
где r ж - плотность жидкости.
Пористость системы можно связать с радиусом пор системы следующей формулой:
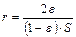 ,
,
где S - удельная поверхность частицы.
Согласно теоретическим представлениям Б.В.Дерягина краевой угол при смачивании пористой поверхности можно оценить по выражению
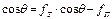 , (30)
, (30)
где f Т и f П - доля поверхности, занятой сплошным твердым телом и порами.
В реальных условиях поверхность твердых тел не является физически и химически чистой. Наличие на поверхности адсорбированных слоев другого вещества, образованных гетерогенным путем или в результате модификации поверхности, приводит к изменению поверхностного натяжения sтг и краевого угла q, что сказывается на работе адгезии. Реальная работа адгезии с учетом адсорбции на твердой поверхности равна:
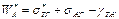 (31)
(31)
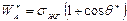 (32)
(32)
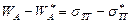 (33)
(33)
Реальная работа адгезии отличается от работы адгезии при участии чистой поверхности на величину 
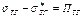 , где
, где 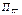 - величина, учитывающая изменение sтг в результате адсорбции.
- величина, учитывающая изменение sтг в результате адсорбции.
Таким образом, смачивание и адгезию можно целенаправленно изменить в желаемом направлении.
2. Методы определения краевого угла смачивания
Адгезия жидкости и ее способность смачивать твердые поверхности характеризуются краевым углом смачивания и работой адгезии. Эти два параметра поддаются измерению. Можно перечислить следующие методы определения КУС:
Прямые измерения краевого угла.
Расчет краевого угла по форме капли.
Определение краевого угла методом погружения.
Дата: 2019-02-19, просмотров: 349.