Метод совмещения. Для получения неискаженных величин элементов фигур (углов и сторон), лежащих в заданной плоскости, пользуются методом совмещения. При этом данная плоскость вращается около одной из своих горизонталей до положения, параллельного плоскости плана.

Определение угла между прямыми

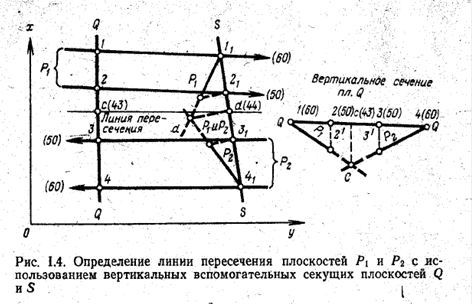
Определение угла между направлениями, например, угла между осью секущей выработки и нормалью к напластованию при переходе от разреза пород по выработке к нор­мальному их разрезу или при переходе от нормальной колонки пород к разрезу их вдоль проектируемой выработки.

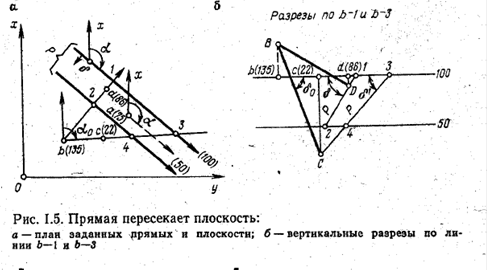
На рис. 1.7 по исходным данным построены наклонные прямые ab и ас и горизонтальная прямая ad . Требуется найти истинную величину угла между наклонными прямыми ab и ас.

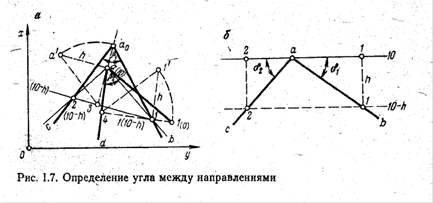
Для проведения на плане (рис. 1.7, а) горизонтали 10—h плоскости, в которой лежат прямые ab и ас, строятся по ним профили (рис. 1.7, б) и на прямых находятся точки 1 к 2, имею­щие одинаковые (10—h ) отметки.

Вращением около этой горизонтали угла 2—а—1 до положения, параллельного плоскости плана, находится совмещенное положение а₀ вершины с этого угла. Точка, а$ соединяется с непо­движными точками 1 и 2. Угол есть искомый угол между прямыми а b и ас.

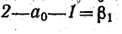
Вопрос 41. Сущность стереографических проекций. Свойства стереографических проекций. Проекции прямых и плоскостей. Решение задач.

Стереографическая проекция — центральная проекция, отображающая двумерную сферу (с одной выколотой точкой) на плоскость.

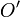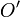Плоскость касается сферы в некоторой точке  (на приведённом рисунке это южный полюс сферы), центром проекции является точка , диаметрально противоположная (на рисунке точка — северный полюс сферы). Через каждую точку 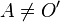сферы проходит единственная прямая, соединяющая 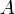и 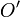. Эта прямая пересекает плоскость в единственной точке 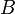, которая, таким образом, является образом точки 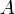при стереографической проекции. В результате получается взаимно однозначное отображение сферы с выколотой точкой 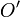на плоскость

 Для того, чтобы получить взаимно однозначное отображение целой сферы, нужно дополнить плоскость элементом, являющимся образом выколотой точки 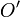. Этот элемент — так называемая бесконечно удалённая точка, обозначаемая символом 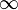. Плоскость, дополненная элементом 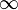, называется расширенной плоскостью. Стереографическая проекция целой сферы на расширенную плоскость является гомеоморфным отображением, при стремлении прообраза 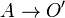его образ .

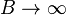Свойства

Стереографическая проекция является конформным отображением — она сохраняет углы между кривыми и форму бесконечно малых фигур. Стереографическая проекция переводит окружности на плоскости в окружности на сфере, а прямые на плоскости — в окружности, проходящие через центр проекции .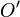

· Стереографическая проекция отображает сопряжённые пучки меридианов и параллелей на сфере в сопряжённые эллиптический и гиперболический пучки окружностей на плоскости.

· Стереографическая проекция осуществляет гомеоморфизм комплексной проективной прямой 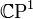на двумерную сферу: для этого нужно рассмотреть двумерную (над полем 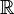) вещественную плоскость с координатами 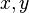как одномерную (над полем 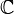) прямую комплексного переменного .

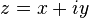· Движения сферы стереографической проекции порождают преобразования Мёбиуса на комплексной плоскости, подобно тому как Гномоническая проекция порождает проективные преобразования на плоскости.