Единицы физических величин, образующие какую-нибудь систему, называются системными единицами, а единицы, не входящие ни в одну из систем, - внесистемными например, тонна, литр, час, сутки и т.д. Впервые понятие о системе единиц физических величин ввел немецкий ученый К.Гаусс. Первоначально были созданы системы единиц, основанные на трех основных единицах, принятых в той или иной стране, например, для метрических единиц распространение получила система МКС (метр, килограмм, секунда). В научных трудах по физике до настоящего времени используется система СГС (сантиметр, грамм, секунда). В технике используется система единиц МКГСС (метр, килограмм- силы, секунда), но из-за сходности наименования единицы силы - килограмм-сила и метрической единицы массы- килограмма, а также своей несогласованностью с практическими электрическими единицами она не получила широкое применение.
Использование этих систем не охватывало всех физических величин, поэтому для отдельных отраслей науки и техники системы единиц были расширены путем добавления еще одной основной единицы. Так появилась система тепловых единиц МКСГ (метр, килограмм, секунда, градус), система единиц для электрических и магнитных измерений МКСА (метр, килограмм, секунда, ампер). Быстрый рост науки, техники, экономики, международных связей неудобства использования существующих систем и большого числа внесистемных единиц – все это вызывало необходимость создания единой универсальной системы единиц. Генеральная конференция по мерам и весам в 1954 г. определила шесть основных единиц физических величин, рекомендуемых для их использования в международных отношениях: метр, килограмм, секунда, ампер, градус Кельвина и свеча.
В 1960 г. одиннадцатой Генеральной конференцией по мерам и весам была утверждена Международная система единиц SI (CИ) как наиболее прогрессивная система, унифицирующая единицы измерений в международном масштабе. Система СИ была введена в действие в СССР с 1963 года. Эта система, согласно Стандарту, должна применяться как предпочтительная во всех областях науки и техники. В последующие годы Генеральная конференция приняла ряд дополнений и изменений, в результате чего в системе вместо шести стало семь основных единиц, дополнительные и производные единицы физических величин.
Учитывая, что в ряде областей измерения широко распространены другие системы единиц и некоторые внесистемные единицы, Государственные стандарты допускают к применению для механических измерений системы СГС - (сантиметр, граммы, секунды) и МКГСС (метр, килограмм - сила, секунда), а также внесистемные единицы - микрон, ангстрем, тонна, центнер, бар, литр, миллиметр ртутного столба и др.
В России допущены к применению следующие единицы измерений, указанные Государственными Стандартами:
ГОСТ 7664-61 - механические единицы;
ГОСТ 7932-56 - световые единицы;
ГОСТ 8033-56 - электрические и магнитные единицы;
ГОСТ 8550-61 - тепловые единицы;
ГОСТ 8848-58 - единицы рентгеновского и гамма-излучений и радиоактивности;
ГОСТ 8849-58 - акустические единицы.
Международная система СИ имеет семь основных единиц и две дополнительные. Основные:
Единица длины
- метр – длина пути, которую проходит свет в вакууме за 1/299792458 долю секунды; (м).
Единица массы - килограмм - представлен массой международного прототипа килограмма (цилиндр из платино-иридия размерами 39 на 39 мм); (кг).
В 1899 году было изготовлено 43 образца, Россия получила 2 из них N12 и N26. Первый - Государственный эталон. Второй - эталон копия.
Напоминаем, что килограмм силы – это сила, сообщающая массе, равной массе международного прототипа килограмма, ускорение, равное 9,80665 м/с2; (Н).
Единица времени - секунда – продолжительность, равная 9 192 631 770 периодам излучения, которая соответствует переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133 при отсутствии возмущения со стороны внешних полей; (с).
Единица силы электрического тока - ампер - сила не изменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенным на расстоянии 1м руг от друга в вакууме, вызвал бы на каждом участке проводника длиной 1м силу взаимодействия, равную 2·10-7 Н; (А).
Единица термодинамической температуры - кельвин – 1/273,16 часть термодинамической температуры тройной точки воды; допускается также применение шкалы Цельсия; (К).
Единица количества вещества – моль – количество вещества системы, содержащей столько же структурных элементов (атомов, молекул, электронов и др.), сколько атомов содержится в углероде-12 массой 0,012 кг; (моль).
Единица силы света – кандела – сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540·1012 Гц, энергетическая сила которого в этом направлении составляет 1/683 Вт/ср; (К).
Дополнительные:
Единица плоского угла - радиан - угол между двумя радиусами окружности, длина дуги между которыми равна радиусу; (рад). В градусном исчислении радиан равен 57º17'48
Единица телесного угла - стерадиан - угол, вершина которого расположена в центре сферы и который вырезает на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы; (ср).
Радиан и стерадиан применяют в основном для теоретических построений и расчетов (например, в светотехнике – стерадиан), для практических прямых измерений их не используют, а плоские углы чаще всего измеряют в угловых градусах, минутах и секундах. Эти внесистемные единицы допущены к применению наравне с единицами Международной системы и в них градуировано большинство угломерных приборов.
В практике измерений часто применяют разрешенные внесистемные единицы например, для массы - тонна; для времени - минута, час, сутки, неделя, месяц, год, и т.д.
2. Модели измерительного процесса
Всякая реальная система, материальный объект характеризуется бесконечным числом переменных. Когда мы описываем, характеризуем систему, мы, исходя из своих предположений, делаем бесконечное число различных выборов из конечного числа переменных. Таким образом, фактически исследуется не подлинная система, не подлинное физическое явление, а его модель, в определенном смысле подобная истинной системе.
Модель - система, не отличимая от моделируемого объекта в отношении некоторых его свойств, именуемых существенными, и отличная от него в отношении других свойств, называемых несущественными.
В теории моделирования различают три принципиальных способа.
Полное моделирование - обеспечивается подобие движения материи во времени и пространстве. Различие между объектом исследования и моделью количественное, масштабное.
Неполное моделирование - здесь протекание основных процессов, характеризующих изучаемое явление или процесс, подобно только частично.
Приближенное моделирование - способ, применяемый наиболее часто, при котором некоторые факторы, влияющие на процесс, но не оказывающие на него решающего действия, либо вовсе не моделируются либо моделируются приближенно, грубо.
При современных исследованиях под моделью стали понимать и круг научных гипотез, позволяющих описывать известные и предсказывать новые явления.
Любое понятие, определенное через способ измерения или через другие сопоставимые и измеримые понятия, отделяется от своего прообраза и становится моделью.
Для получения оценок качества измерения и выработки требования к измерительной аппаратуре прибегают к моделям измерительного процесса, выделяя главные явления и факторы.
Каноническая модель измерительного процесса, понимаемого как эксперимент, условия которого строго определены и соблюдаются, строилась в метрологии при следующих ограничениях:
- измеряемая физическая величина сохраняет неизменным на протяжении всего цикла измерения свое истинное значение, которое можно охарактеризовать ее одним, так называемым действительным значением, лежащем внутри интервала остаточной неопределенности (доверительный интервал);
- время измерения не ограничено и сравнение с мерой может выполняться принципиально как угодно долго и тщательно;
- внешние условия и влияющие на результат факторы точно определены.
Но так как практические задачи измерительной техники отличаются от идеализированного метрологического эксперимента сравнения с мерой, то и изменяется модель измерительного процесса, т.е. производится оценка качества измерения на основе теоретически-вероятностного подхода.
Вероятностная модель измерительного процесса (информационная) - измеряемая физическая величина рассматривается как случайный процесс, содержащий интересующую нас информацию о состоянии исследуемого объекта и описывается случайной последовательностью действительных значений или же обобщенными характеристиками такой последовательности , истинное (мгновенное) значение измеряемой величины может оставаться неопределенным на данном интервале процесса измерения;
- измерение, в общем случае, рассматривается как последовательность операций, время выполнения которых ограничено и конечно; непосредственное сравнение с мерой неосуществимо;
- характеристики измерительного устройства могут изменяться во времени и под влиянием внешних факторов, переменных по своей природе /эти изменения рассматриваются как случайные процессы, влияющие на конечную неопределенность результата измерений/.
Указанные раньше основные группы классической модели являются частным случаем вероятностной модели. Необходимость введения вероятностной модели измерительного процесса вызвана прежде всего задачей оценки качества измерения меняющихся во времени величин (проблема динамической точности), которая не нашла удовлетворительного решения в рамках классической метрологии.
ПОГРЕШНОСТИ ИЗМЕРЕНИЙ.
КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
Погрешность измерений - это отклонение результата измерений от истинного значения измеряемой величины. Погрешность средств измерений зависит от условий проведения измерений. При этом различают основные и дополнительные погрешности.
Основная погрешность - погрешность, существующая при так называемых нормальных условиях, которые указаны в нормативных документах, регламентирующих правила испытания и эксплуатации данного средства измерений.
Дополнительная погрешность возникает при отклонении условий испытания и эксплуатации средства измерения от нормальных. Она нормируется значением погрешности, вызванной отклонением одной из влияющих величин от ее нормирующего значения или выходом ее за пределы нормальной области значений.
По способу выражения различают абсолютные и относительные погрешности.
Абсолютная погрешность измерения - погрешность измерений, выраженная в единицах измеряемой величины (1.1)
Относительная погрешность измерения - погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному значению измеряемой величины, в процентах
d = D х / хд × 100%. (2.1)
Чтобы можно было сравнить по точности измерительные приборы с разными пределами измерений, введено понятие приведенной погрешности измерительного прибора, под которой понимают отношение абсолютной погрешности к нормирующему значению, которое принимается равным верхнему пределу измерений (если нулевая отметка находится на краю или вне шкалы) или диапазону измерения (если нулевая отметка находится внутри диапазона измерений), в процентах
g = (хизм - хд ) / хнор ×100%. (2.2)
Систематическая погрешность измерения - составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. В соответствии с этим определением систематические погрешности разделяются на постоянные и переменные. Переменные в свою очередь могут быть прогрессирующими, периодическими и изменяющимися по сложному закону.
Постоянными систематическими погрешностями называются такие, которые остаются неизменными в течение всей серии данных измерений, например, погрешность из-за неточной подгонки образцовой меры, погрешность из-за неточной установки указателя прибора на нуль и т. п.
Переменные систематические погрешности изменяются в процессе измерений. Если при измерениях погрешность монотонно убывает или возрастает, то она называется прогрессирующей. Так, например, монотонно меняется погрешность из-за разряда батареи или аккумулятора, если результат измерений зависит от напряжения питания. Периодическая систематическая погрешность - погрешность, значение которой является периодической функцией времени. Ее примером может являться погрешность, вызванная суточными изменениями напряжения питания электрической сети. Систематическая погрешность может изменяться и по некоторому сложному закону. Таковы, например, погрешности, вызванные неточностью нанесения шкалы прибора, погрешность электрического счетчика при различном значении нагрузки, погрешность, вызванная изменениями температуры окружающей среды, и др.
Случайная погрешность измерения - составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины. Например, погрешность измерений из-за вариации показаний измерительного прибора; погрешность округления, при считывании показаний измерительного прибора. Случайная погрешность не может быть исключена из результата измерения, но может быть уменьшена путем статистической обработки совокупности наблюдений.
Таким образом, погрешность результата измерения представляет собой сумму систематической и случайной составляющих.
Встречается также грубая погрешность или промах - погрешность измерения, существенно превышающая ожидаемую при данных условиях погрешность. Источником грубой погрешности может быть неправильный отсчет показаний средств измерений или непредвиденное кратковременное воздействие какого-либо фактора, например, резкое кратковременное изменение напряжения питающей сети. Грубые погрешности выявляются при статической обработке ряда наблюдений, и соответствующие результаты наблюдений должны быть исключены.
По зависимости от измеряемой величины погрешности средства измерений разделяют на аддитивные и мультипликативные.
Аддитивные (абсолютные) погрешности не зависят от измеряемой величины.
Мультипликативные (относительные) погрешности изменяются пропорционально измеряемой величине. Соответственно относительная аддитивная погрешность обратно пропорциональна значению измеряемой величины, а относительная мультипликативная - от него не зависит. Аддитивную погрешность иногда называют погрешностью нуля, а мультипликативную -погрешностью чувствительности. Реально погрешность средства измерений включает в себя обе указанные составляющие.
СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ
Природа и происхождение систематических погрешностей обычно обусловлены спецификой конкретного эксперимента. Поэтому обнаружение и исключение систематических погрешностей во многом зависит от мастерства экспериментатора, от того, насколько глубоко он изучил конкретные условия проведения измерений и особенности применяемых им средств и методов. Вместе с тем существуют некоторые общие причины возникновения систематических погрешностей, в соответствии с которыми их подразделяют на методические, инструментальные и субъективные.
Методические погрешности происходят от несовершенства метода измерения, использования упрощающих предположений и допущений при выводе применяемых формул, влияния измерительного прибора на объект измерения. Например, измерение температуры с помощью термопары может содержать методическую погрешность, вызванную нарушением температурного режима исследуемого объекта (вследствие внесения термопары).
Инструментальные погрешности зависят от погрешностей применяемых средств измерений. Неточность градуировки, конструктивные несовершенства, изменения характеристик прибора в процессе эксплуатации и т. д. являются причинами инструментальных погрешностей. Эта погрешность в свою очередь подразделяется на основную и дополнительную.
Основная погрешность средства измерений - это погрешность в условиях, принятых за нормальные, т. е. при нормальных значениях всех величин, влияющих на результат измерения (температуры, влажности, напряжения питания и т. п.).
Дополнительная погрешность средства измерений - погрешность, дополнительно возникающая при отличии значений влияющих величин от нормальных. Обычно различают отдельные составляющие дополнительной погрешности, например температурную погрешность, погрешность из-за изменения напряжения питания и т. п.
Все эти погрешности отличают от инструментальных (ГОСТ 8.009-84), поскольку они связаны не столько с самими средствами измерений, сколько с условиями, при которых они работают. Их устранение производится иными способами, нежели устранение инструментальных погрешностей.
Субъективные погрешности вызываются неправильными отсчетами показаний прибора человеком (оператором). Это может случиться, например, из-за неправильного направления взгляда при наблюдении за показаниями стрелочного прибора (погрешность от параллакса). Использование цифровых приборов и автоматических методов измерения позволяет исключить такого рода погрешности.
Обнаружение причин и источников систематических погрешностей позволяет принять меры к их устранению или исключению посредством введения поправки.
Поправкой называется значение величины, одноименной с измеряемой, которое нужно прибавить к полученному при измерении значению величины с целью исключения систематической погрешности.
В некоторых случаях используют поправочный множитель - число, на которое умножают результат измерения для исключения систематической погрешности.
Поправка или поправочный множитель определяется при помощи поверки технических средства, составления и использования соответствующих таблиц и графиков. Применяются также расчетные способы нахождения поправочных значений.
Существуют специальные методы организации измерений, устраняющие систематические погрешности. К ним относятся, например, метод замещения и метод компенсации погрешности по знаку. Метод замещения заключается в том, что измеряемая величина замещается известной величиной, получаемой при помощи регулируемой меры. Если такое замещение производится без каких-либо других изменений в экспериментальной установке и после замещения установлены те же показания приборов, то измеряемая величина равняется известной величине, значение которой отсчитывается по указателю регулируемой меры. Этот прием позволяет исключить постоянные систематические погрешности. Погрешность измерения при использовании метода замещения определяется погрешностью меры и погрешностью, возникающей при отсчете значения величины, замещающей неизвестную.
Метод компенсации погрешности по знаку применяется для исключения систематических погрешностей, которые в зависимости от условий измерения могут входить в результат измерения с тем или иным знаком (погрешность от термо-ЭДС, от влияния напряженности постоянного электрического или магнитного поля и др.). В этом случае можно провести измерения дважды так, чтобы погрешность входила в результаты измерений один раз с одним знаком, а другой раз - с обратным. Среднее значение из двух полученных результатов является окончательным результатом измерения, свободным от указанных выше систематических погрешностей.
При проведении автоматических измерений широко используются схемные методы коррекции систематических погрешностей. Компенсационное включение преобразователей, различные цепи температурной и частотной коррекции являются примерами их реализации.
Новые возможности появились в результате внедрения в измерительную технику средств, содержащих микропроцессорные системы. С помощью последних удается производить исключение или коррекцию многих видов систематических погрешностей. Особенно это относится к инструментальным погрешностям. Автоматическое введение поправок, связанных с неточностями градуировки, расчет и исключение дополнительных погрешностей, исключение погрешностей, обусловленных смещением нуля - это и другие корректировки позволяют существенно повысить точность измерений.
Следует, однако, заметить, что какая-то часть систематической погрешности, несмотря на все усилия, остается неисключенной. Эта часть входит в результат измерения и искажает его. Она может быть оценена исходя из сведений о метрологических характеристиках использованных технических средств. Если таких сведений недостаточно, то может быть полезным сравнение измеренных значений с аналогичными результатами, полученными в других лабораториях другими лицами.
СЛУЧАЙНЫЕ ПОГРЕШНОСТИ
Теория погрешностей, использующая математический аппарат теории вероятностей, основывается на аналогии между появлением случайных погрешностей при многократно повторенных измерениях и появлением случайных событий. Из теории вероятностей известно, что для характеристики случайных величин, в нашем случае погрешностей прибора или измерения (вместе с их систематической составляющей), необходимо определить их закон распределения.
В теории случайных погрешностей формулируются две аксиомы.
Аксиома симметрии (случайности) - при очень большом числе измерений случайные погрешности, равные по величине, но различные по знаку, встречаются одинаково часто.
Аксиома распределения - чаще всего встречаются меньшие погрешности, а большие погрешности встречаются тем реже, чем они больше.
Если эти аксиомы соблюдаются, то при неограниченном увеличении числа независимых причин, вызывающих погрешности, мы имеем нормальный закон распределения случайной погрешности.
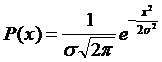 (2.3)
(2.3)
где P(х) - плотность вероятности случайной величины X; s - среднее квадратическое отклонение.
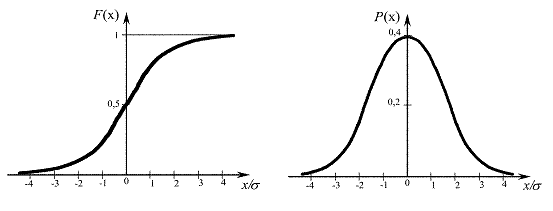
Рис. 2.1. Интегральный и дифференциальный законы распределения
Одно из нарушений нормального закона распределения погрешностей при соблюдении аксиом состоит в появлении плосковершинности и островершинности, как показано на рис. 2.2.
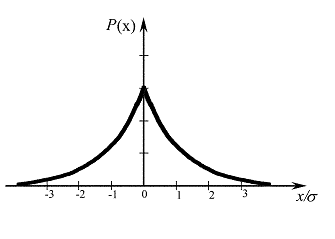
Рис. 2.2. Островершинное распределение
В пределе для плосковершинного распределения, когда уже аксиома не соблюдается, оно превращается в равномерное.
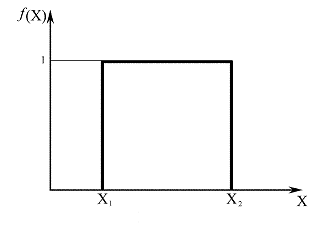
Рис. 2.3. Равномерное (равновероятное) распределение
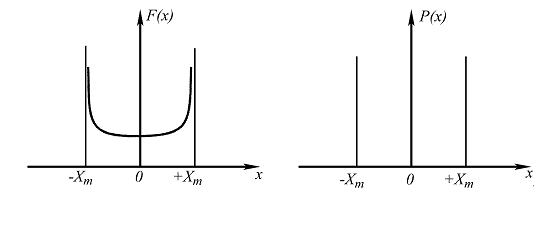
Рис. 2.4. Двухмодальное распределение
Модой дискретной случайной величины называют ее наиболее вероятное значение, а для непрерывной случайной величины модой является то значение, при котором плотность вероятности достигает максимума. В пределе такое двухмодальное распределение может превратиться в распределение, когда единственно наблюдаемыми погрешностями будут только погрешности ±XmaX (см. рис. 2.4). Например, погрешность от люфта в кинетической цепи, погрешность от гистерезиса имеют вид двухзначной дискретной погрешности.
Дата: 2019-02-19, просмотров: 403.