Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Из выражений для симметричных составляющих токов и напряжений в месте несимметричного КЗ (табл.11.2), замечаем, что токи обратной и нулевой последовательности и напряжения всех последовательностей пропорциональны току прямой последовательности в месте КЗ. Следовательно, задача расчета любого несимметричного КЗ прежде всего состоит в вычислении тока прямой последовательности в месте рассматриваемого вида КЗ.

Таблица 1 1 .2

Определяемая величина

Виды КЗ

К(2) К(1) К(1,1) Токи в месте КЗ а) Прямой последовательности в фазе А IкА1 б. Oбратной последовательности в фазе А IкА2 в.Нулевой последовательности IкА0 ЕА/j(Х1+Х2)   -IкА1   0 ЕА/j(Х1+Х2+Хо) IкА1 IкА1   ЕА/j(X1+Х2║Х0) -IкА1Z0/ (Zо+Z2) -IкА1Z2/ (Z0+Z2) Полный ток КЗ а) B фазе А IкА   б) B фазе В IкВ   в) B фазе С IкС   0   -j√3IкА1   j √IкА1   3IкА1   0   0   0 IкА1(a²-Z2+ аZ0/Z2+Z0) IкА1(а-Z2+ аZ0/(Z2+Z0)) Напряжения в месте КЗ а) прямой последовательности UкА1   б) обратной последовательности UкА2   в) нулевой последовательности UкА0   г) фазы А UкА   д) фазы В UкВ   е) фазы С UкС IкА1 Z2 IкА1 Z2   0   2IкА1 Z2   -IкА1Z2 IкА1 Z2 IкА1(Z2+Zо)   -IкА1 Zо   -IкА1 Zо   0 IкА1[(а²-а) Z2+(а²-1)Zо] IкА1[(а-а²) Z2+(а-1)Zо] IкА1Z2 Z0/ (Z2+Z0) IкА1Z2Z0/ (Z2+Z0) IкА1 Z2 Z0/ (Z2+Z0) 3IкА1 Z2 Z0/ (Z2+Z0) 0   0

 

Величина тока прямой последовательности определяется так:

при двухфазном КЗ:

;

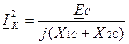при однофазном КЗ:

;

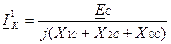при двухфазном КЗ на землю:

;

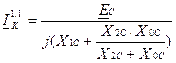Структура приведенных выражений позволяет ток прямой последовательности при любом (n) виде несимметричного КЗ выразить в общем виде:

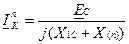,                                  (11.5)

где 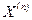 - дополнительная реактивность, величина которой для каждого вида КЗ определяется только значениями Х2 C и Х0 C.

 

Таблица 11.3

Значения дополнительного реактанса Х( n ) и коэффициента m(n)

Вид КЗ	(n)	Х (n)	m(n)
трехфазное	(3)	0	1
двухфазное	(2)	Х2	√3
однофазное	(1)	Х2 + Хо	3
двухфазное на землю	(1,1)	Х2 Хо /(Х2 + Хо)	√ 3√1- Х2 Хо /(Х2 + Хо)²

Абсолютная величина полного тока поврежденных фаз в месте КЗ пропорциональна току прямой последовательности, что позволяет записать общее выражение:

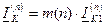;                                       (11.6)

где m(n) - коэффициент пропорциональности, зависящий от вида КЗ

Значения Х(n) и m(n) для различных видов КЗ приведены в табл.11.3.

Обобщенная запись для тока (11.5) позволила Н.Н.Щедрину впервые сформулировать важное положение, которое называют правилом эквивалентности прямой последовательности:

Ток прямой последовательности любого несимметричного КЗ может быть определен как ток при трехфазном КЗ в точке, удаленной от действительной точки КЗ на дополнительное сопротивление Х(n), которое не зависит от параметров схемы прямой последовательности и для каждого вида КЗ определяется результирующими сопротивлениями обратной последовательности Х2с и нулевой последовательности Х0с относительно точки возникшей несимметрии.