Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Конспект лекций

по курсу: «Электромагнитные переходные процессы»

 

Часть 2: ЭЛЕКТРОМАГНИТНЫЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ

ПРИ нарушении СИММЕТРИИ системы

 

для студентов специальности

6.090603 «Электротехнические системы электропотребления

всех форм обучения

 

Сумы 2008

Поперечная несимметрия

 

Общие положения

 

Расчеты токов трехфазных КЗ в трехфазных симметричных сетях производятся на одну фазу вследствие подобия явлений, происходящих в каждой из фаз и равенства значений одноименных величин.

При несимметрии в произвольной точке системы сопротивления в фазах неодинаковы и по этим причинам явления по фазам различны. Неодинаковы в этом случае токи, напряжения и углы сдвига между ними в различных фазах. Для определения токов и напряжений в любой фазе несимметричной системы необходимо составить схему замещения и написать необходимое число уравнений с учетом взаимоиндукции, что усложняет решение задач.

Сравнительно просто расчеты несимметричных режимов в трехфазных сетях осуществляются с помощью метода симметричных составляющих. Вычисление токов и напряжений в этом случае сводятся к определению этих величин при некотором фиктивном трехфазном КЗ, что дает возможность вновь воспользоваться однолинейной схемой замещения и произвести расчет на одну фазу. В этом заключается одно из основных достоинств метода симметричных составляющих.

 

Сопротивления различных последовательностей элементов

Электрических систем

Общие положения

Все сопротивления, которыми характеризуются отдельные элементы в нормальном симметричном режиме, а также в симметричном переходном процессе, по существу являются сопротивлениями прямой последовательности. Этот термин раньше не вводился, так как в схеме протекали токи лишь прямой последовательности. При отсутствии взаимоиндукции между фазами какого-либо элемента его сопротивления прямой, обратной и нулевой последовательности одинаковы, так как они обусловлены только собственной индуктивностью фазы Х₁ = Х₂ = Х₀.

При наличии магнитной связи между фазами реактивное сопротивление определяется с учетом взаимной индуктивности, которое зависит от того, какая последовательность токов протекает по фазам. Для элемента, магнитосвязанные цепи которого неподвижны друг относительно друга, сопротивления прямой и обратной последовательностей одинаковы, так как от перемены чередования фаз взаимоиндукция между фазами такого элемента не изменяется. Таким образом для трансформаторов, воздушных и кабельных линий, реакторов Х₁ = Х₂.

Сопротивление нулевой последовательности всех элементов резко отличается от сопротивления прямой и обратной последовательностей, так как в этом случае взаимоиндукция сказывается иначе, в силу того, что система токов нулевой последовательности совпадает по фазам, в то время как токи прямой и обратной последовательностей по фазам сдвинуты на 120°. Кроме того на величину сопротивления нулевой последовательности оказывает существенное влияние схема соединения фаз рассматриваемого элемента и режим нейтрали..

 

Сопротивление нулевой последовательности реакторов

Реактивное сопротивление реакторов в основном определяется их самоиндукцией. Взаимоиндукция между фазами реактора настолько мала, что практически ею можно пренебречь. По этой причине реактивное сопротивление нулевой последовательности реактора можно считать равным реактивному сопротивлению прямой последовательности, т.е. Х₀=Х₁.

Наименован. элемента

Трехфазное КЗ

Прямая последов.

Обратная последоват.

Нулевая последоват.

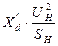
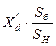
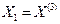
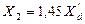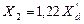
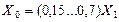
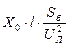
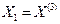
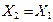
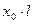
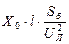
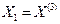
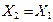
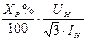
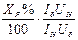
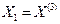
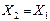
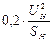
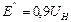
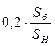
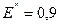
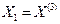
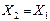
ИЕ ОЕ Синхронный генератор без ДО с ДО Воздушная ЛЭП одноцепная с тросами Х₀ = 3,0 Х₁, одноцепная без тросов Х₀ = 3,5 Х₁, двухцепная с тросами Х₀=4,7Х₁ двухцепная без тросов Х₀ = 5,5 Х₁ Кабельная ЛЭП Х₀ =(3,5...4,7) Х₁, R₀ = 10 r L Токоогранич . реактор Х₀ = Х₁ Асинхронный двигатель Х₀ =( 0,15...0,7) Х₁ Обобщенная нагрузка определяется элементами Двухобмот. трансформ . Определяется соединением обмоток Синхронный двигатель, компенс.                                   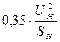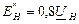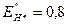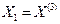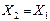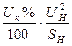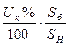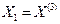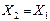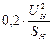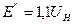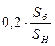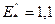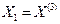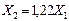допускается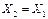 Х₀ =(0,15...0,7)Х₁.

Таблица 1 1 .2

Определяемая величина

Виды КЗ

К(2) К(1) К(1,1) Токи в месте КЗ а) Прямой последовательности в фазе А IкА1 б. Oбратной последовательности в фазе А IкА2 в.Нулевой последовательности IкА0 ЕА/j(Х1+Х2)   -IкА1   0 ЕА/j(Х1+Х2+Хо) IкА1 IкА1   ЕА/j(X1+Х2║Х0) -IкА1Z0/ (Zо+Z2) -IкА1Z2/ (Z0+Z2) Полный ток КЗ а) B фазе А IкА   б) B фазе В IкВ   в) B фазе С IкС   0   -j√3IкА1   j √IкА1   3IкА1   0   0   0 IкА1(a²-Z2+ аZ0/Z2+Z0) IкА1(а-Z2+ аZ0/(Z2+Z0)) Напряжения в месте КЗ а) прямой последовательности UкА1   б) обратной последовательности UкА2   в) нулевой последовательности UкА0   г) фазы А UкА   д) фазы В UкВ   е) фазы С UкС IкА1 Z2 IкА1 Z2   0   2IкА1 Z2   -IкА1Z2 IкА1 Z2 IкА1(Z2+Zо)   -IкА1 Zо   -IкА1 Zо   0 IкА1[(а²-а) Z2+(а²-1)Zо] IкА1[(а-а²) Z2+(а-1)Zо] IкА1Z2 Z0/ (Z2+Z0) IкА1Z2Z0/ (Z2+Z0) IкА1 Z2 Z0/ (Z2+Z0) 3IкА1 Z2 Z0/ (Z2+Z0) 0   0

 

Величина тока прямой последовательности определяется так:

при двухфазном КЗ:

;

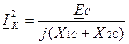при однофазном КЗ:

;

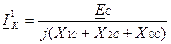при двухфазном КЗ на землю:

;

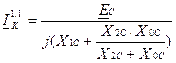Структура приведенных выражений позволяет ток прямой последовательности при любом (n) виде несимметричного КЗ выразить в общем виде:

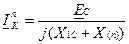,                                  (11.5)

где 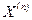 - дополнительная реактивность, величина которой для каждого вида КЗ определяется только значениями Х2 C и Х0 C.

 

Таблица 11.3

Ток прямой последовательности любого несимметричного КЗ может быть определен как ток при трехфазном КЗ в точке, удаленной от действительной точки КЗ на дополнительное сопротивление Х(n), которое не зависит от параметров схемы прямой последовательности и для каждого вида КЗ определяется результирующими сопротивлениями обратной последовательности Х2с и нулевой последовательности Х0с относительно точки возникшей несимметрии.

Поперечной несимметрии

 

Расчеты несимметричных КЗ проводят с использованием метода симметричных составляющих, согласно которому любая несимметричная трехфазная система напряжений, токов, потоков и т.п. заменяется тремя симметричными трехфазными системами прямой, обратной и нулевой последовательности.

При расчетах токов несимметричных КЗ применяют правило эквивалентности прямой последовательности, на основании которого ток прямой последовательности при любом несимметричном КЗ численно равен току при некотором эквивалентном трехфазном КЗ в точке, удаленной на величину Х( n ) от действительной точки КЗ. Следовательно, все методы расчета токов при трехфазных КЗ приемлемы и для определения тока любого несимметричного КЗ.

 

Конспект лекций

по курсу: «Электромагнитные переходные процессы»

 

Часть 2: ЭЛЕКТРОМАГНИТНЫЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ

ПРИ нарушении СИММЕТРИИ системы

 

для студентов специальности

6.090603 «Электротехнические системы электропотребления

всех форм обучения

 

Сумы 2008

Поперечная несимметрия

 

Общие положения

 

Расчеты токов трехфазных КЗ в трехфазных симметричных сетях производятся на одну фазу вследствие подобия явлений, происходящих в каждой из фаз и равенства значений одноименных величин.

При несимметрии в произвольной точке системы сопротивления в фазах неодинаковы и по этим причинам явления по фазам различны. Неодинаковы в этом случае токи, напряжения и углы сдвига между ними в различных фазах. Для определения токов и напряжений в любой фазе несимметричной системы необходимо составить схему замещения и написать необходимое число уравнений с учетом взаимоиндукции, что усложняет решение задач.

Сравнительно просто расчеты несимметричных режимов в трехфазных сетях осуществляются с помощью метода симметричных составляющих. Вычисление токов и напряжений в этом случае сводятся к определению этих величин при некотором фиктивном трехфазном КЗ, что дает возможность вновь воспользоваться однолинейной схемой замещения и произвести расчет на одну фазу. В этом заключается одно из основных достоинств метода симметричных составляющих.

 

Метод симметричных составляющих

 

В соответствии с методом симметричных составляющих произвольную несимметричную систему трех векторов А, В, С можно разложить однозначно на три симметричные системы:

– систему векторов прямой последовательности А₁; В₁; С₁;

– систему векторов обратной последовательности А₂; В₂; С₂;

– систему векторов нулевой последовательности А₀; В₀; С₀;

Согласно условию разложения имеем:

А = А₁ + А₂ + А₀,

В = В₁ + В₂ + В₀,                                            (11.1)

С = С₁ + С₂ + С₀.

Для сведения уравнений (11.1) к трем неизвестным вводят оператор фазы а. Модуль оператора фазы равен 1. Таким образом, если любой вектор умножить на а, то модуль вектора не изменится, а лишь произойдет его поворот на 120˚ против часовой стрелки. Благодаря этому свойству можно векторы каждой из симметричных систем (прямой, обратной, нулевой) выразить через один вектор той же системы, т.е. три неизвестных в уравнении (11.1) свести к одному.

Оператор фазы а определяется из соотношений:    

;

; .

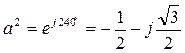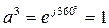Если принять в качестве основной фазу А, то систему (11.1) при помощи оператора фазы а можно представить в следующем виде:

А = А₁ + А₂ + А₀,

                                      В = а² А₁ + аА₂ + А₀,                                      (11.2)

С = а А₁ + а² А₂ + А₀

Совместное решение системы уравнений (11.2) дает:

А ₁ = (А + а В + а² С) / 3;

 А₂ = (А + а² В + а С) / 3;                                  (11.3)

А ₀ = (А + В + С) / 3.

11.3. Основные уравнения.

 

ЭДС симметричного трехфазного источника питания образуют симметричную систему векторов прямой последовательности. При нормальной симметричной нагрузке или при трехфазном КЗ такая ЭДС способна вызвать только токи прямой последовательности, так как напряжения и ЭДС других последовательностей в таких режимах отсутствуют.

При несимметричных КЗ в месте повреждения возникают несимметричные напряжения, вследствие нарушения симметрии режима. Вся схема в целом и по частям продолжает оставаться симметричной. Появляющиеся при этом токи обратной и нулевой последовательности вызывают в элементах схемы соответствующие магнитные потоки и падения напряжения.

ЭДС контуров токов обратной и нулевой последовательности можно учитывать падением напряжения в реактивном сопротивлении машины той или иной последовательности. В силу указанных соображений можно считать, что при любом режиме генератор вырабатывает ЭДС только прямой последовательности, а ЭДС обратной и нулевой последовательности генератора равны нулю.

В соответствии с изложенным для произвольного несимметричного КЗ основные уравнения в соответствии с вторым законом Кирхгофа отдельно для каждой последовательности будут иметь вид:

 U_К1 = Е - Z₁·I_К1;

U _К2 = 0 - Z ₂ · I _К2 ;                                            (11.4)

U _К0 = 0 - Z ₀ · I _К0 ,

где U_К1, U_К2, U_К0, I_К1, I_К2, I_К0 - симметричные составляющие напряжения и тока в месте КЗ;

    Е - результирующая ЭДС схемы прямой последовательности относительно точки КЗ;

    Z₁, Z₂, Z₃ - результирующие сопротивления схем соответствующих последовательностей относительно точки КЗ.

Уравнения (11.4) содержат шесть неизвестных величин: три составляющие напряжения и три составляющие тока. Недостающие уравнения для определения неизвестных величин получают из граничных условий, которыми характеризуется тот или иной вид несимметричного повреждения.