Балансовая стоимость акции = Итог раздела «Капитал и резервы» / число обыкновенных акций = 10664 тыс. руб. / 124 тыс. шт. = 86 руб.
Следовательно, при номинальной стоимости акции 1 руб., ее балансовая стоимость составляет 86 руб. По балансовой стоимости акции не продаются и не покупаются, она лишь свидетельствует о величине собственных средств акционерного общества, приходящихся на одну акцию.
Динамика балансовой стоимости акций в определенной мере отражает результаты деятельности акционерного общества. Если нет эмиссии дополнительных акций и не проводятся переоценки основных фондов, то динамика балансовой стоимости акций определяется результатами деятельности акционерного общества: при получении прибыли балансовая стоимость акций увеличивается, убытков – уменьшается. Полученная предприятием прибыль приводит к росту балансовой стоимости акций только в том случае, если направляется на развитие производства, в фонд накопления и другие фонды общества.
Рыночная цена, или курс акций — это та цена, по которой акции свободно продаются и покупаются на рынке. Номинал акции при этом значения не имеет, и акция меньшего номинала может продаваться по более высокой цене. Для инвестора имеет значение, какую прибыль приносит акция в данный момент и каковы перспективы получения прибыли в будущем.
Теоретически цена акций определяется либо как величина собственного капитала эмитента деленного на число эмитированных акций, либо как текущая стоимость будущих денежных поступлений. При это практическое использование этих теоретических оценок затруднено ввиду условности величины уставного капитала, а также полной неопределенности дивидендной политики в будущем.
Модели оценки стоимости акций определяются на основе анализа следующих факторов:
· вид акций – привилегированная или простая,
· сумма дивидендов, предполагаемая к получению в конкретном периоде,
· ожидаемая курсовая стоимость акции в конце периода ее реализации,
· ожидаемая норма прибыли,
· число периодов использования акций.
Привилегированные акции
Модель оценки стоимости привилегированных акций основана на том, что эти акции дают право их собственникам на получение регулярных дивидендных выплат в фиксированном размере. Для определения цены привилегированной акции, имеющей фиксированную величину дивиденда, необходимо найти приведенную стоимость всех дивидендов, которые будут выплачены инвестору. Таким образом, общий подход к определению цены привилегированной акции соответствует рассмотренной нами ранее модели определения цены облигации. При этом надо учитывать, что облигация является бессрочной ценной бумагой; инвестор, однако, может продать ее через определенное время.
Если инвестор предполагает держать облигацию n периодов, то ее цена может быть определена из следующего выражения:
P = D/(1+R)1+ D/(1+R)2+ … +D/(1+R)n + Рs/(1+R)n ,
где Р - стоимость акции; D - дивиденд на акцию; R - требуемая норма прибыли на данный тип инвестиций, Рs – стоимость акции на момент продажи.
Если инвестор предполагает держать облигацию достаточно долго, то ее цене может быть определена по формуле:
P = D/(1+R)1+ D/(1+R)2+ … +D/(1+R)n +…
Как было показано ранее при достаточно большом n данное выражение может быть преобразовано к виду:
P = D/R
Задача. По привилегированной акции номиналом 50 долл. выплачивается дивиденд в размере 10 долл. Определить цену акции, если требуемая норма прибыли на данный тип акций составляет 20% годовых.
Применяя полученную формулу, имеем:
P = 10/0,2 = 50 долл.
Существует ряд подходов для определения требуемой нормы прибыли акции. Прежде всего следует ориентироваться на альтернативные возможности инвестирования с соответствующим уровнем риска. Требуемая норма прибыли по рисковым активам складывается из безрисковой ставки и премии за риск. Так в данном примере требуемая доходность может складываться из безрисковой ставки, составляющей 12% и премии за риск – 12%.
Обыкновенные акции
Задача определения рыночной цены обыкновенных акций является значительно более сложной, чем привилегированных акций. Обусловлено это следующими обстоятельствами. Во-первых, дивиденд по обыкновенным акциям заранее не объявляется и можно исходить лишь из предположения о его предстоящем уровне. Во-вторых, на выплату дивидендов идет только часть чистой прибыли компании, другая часть в виде нераспределенной прибыли остается в компании и используется на развитие производства.
При этом величина нераспределенной прибыли определяет потенциал роста прибыли компании в будущем. По существу, нераспределенная прибыль является для акционеров капитализированным дивидендом, и ее увеличение ведет к росту рыночной цены акции. В результате доход инвестора от владения акцией складывается из величины получаемых дивидендов и прироста курсовой стоимости акции. При этом необходимо учитывать, что курсовая стоимость может не только вырасти, но и снизиться.
Таким образом, при определении цены обыкновенных акций необходимо учитывать не только размер дивиденда, но и прирост стоимости акции.
Задача. Прогнозируемая стоимость акции через год составляет 700 рублей, ожидаемые дивиденды – 100 руб., а требуемая норма прибыли – 25%. Необходимо определить цену акции. Эта цена определяется как приведенная стоимость будущих денежных поступлений, которые складываются из дивидендных выплат и цены акции на момент ее продажи:
P = (D+P1)/(1+R) = (100+700)/(1+0.25)1 = 640 руб.
Инвестор может владеть акциями более одного года. В этом случае исходя из того, что доход на акцию обеспечивается за счет получения дивидендов и роста курсовой стоимости выражение для определения цены акции может быть представлено в виде:
P = D1/(1+R)1+ D2/(1+R)2+ … +Dn/(1+R)n+ Рn/(1+R)n =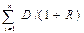 
i + Рn/(1+R)n
где Р — искомая цена акции; D 1, D 2 ... Dn — ожидаемые дивиденды первого, второго, n-го года; R — требуемая норма прибыли на акцию.
Таким образом, мы получили выражение для определения цены акции. Однако его практическое использование затруднено в силу сложности задачи прогнозирования дивидендных выплат и будущей стоимости акции.
В связи с этим рассмотрим ряд частных случаев расчета цены акции. Акция является бессрочной ценной бумагой. При этом в отдельные периоды времени доход может быть получен только за счет действия одного фактора (дивиденды или рост курсовой стоимости). Если, наПример, компания в течение ряда лет не выплачивает дивиденды, а вся прибыль расходуется на развитие компании, то для определения цены акции может быть использовано выражение:
P = Рn/(1+R)n.
где R — ожидаемая норма прибыли на акцию, P, Рn — текущая стоимость акции и ее стоимость через n периодов.
Задача. На фондовом рынке продаются акции фирмы В по цене 100 руб. за штуку. По имеющимся прогнозам дивиденды не будут выплачиваться в течение пяти лет, а вся прибыль будет использоваться на развитие производства. Какова должна быть цена акции через пять лет для обеспечения нормы прибыли в размере 20% годовых. Применяя представленную выше формулу получим:
Рn =100х(1+0,2)5 =248,8 руб.
Таким образом, для обеспечения требуемой норму прибыли цена акции B через три года должна достичь 248,8 руб. Если по проведенным оценкам цена акции через три года будет ниже этой суммы, то вложения в покупку акций B не обеспечат требуемой нормы прибыли, и от покупки акций следует отказаться.
В ряде случаев вся прибыль компании может направляться на выплату дивидендов. В такой ситуации можно предположить, что цена акции остается неизменной и требуемая доходность обеспечивается только за счет дивидендных выплат.
Задача. На фондовом рынке продаются акции компании C. В течение последних лет вся прибыль компании направлялась на выплату дивидендов, которые составляли 100 руб. на акцию. Предполагается, что в течение ближайших трех лет вся прибыль также будет направляться на выплату дивидендов и их уровень останется прежним. Определить цену акции при условии, что она остается неизменной в течение рассматриваемого периода. Какой должна быть цена акции, чтобы обеспечить норму прибыли 
в размере 20% годовых. Для определения цены акции в данном случае может быть использовано следующее соотношение:
P = 100/(1+0,2)1+ 100/(1+0,2)2+100/(1+0,2)3+Р/(1+0,2)3 = 500,83 руб.
В предыдущих примерах мы предположили, что доход на акцию обеспечивается либо за счет получения дивидендов, либо за счет роста курсовой стоимости. Такие случаи вполне возможны в отдельные короткие периоды времени. Если же рассматривать более продолжительные периоды времени, то доход на акцию обеспечивается за счет действия обоих факторов: выплаты дивидендов и роста курсовой стоимости.
Модель определения стоимости акций во многом зависит от поведения инвестора. Если инвестор планирует держать акцию в течение заранее определенного периода времени, то для определения цены акции может быть использовано поученное выше выражение
P = D1/(1+R)1+ D2/(1+R)2+ … +Dn/(1+R)n+ Рn/(1+R)n = 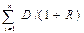i + Рn/(1+R)n
Экономическое содержание данной модели состоит в том, что текущая реальная стоимость акции, используемой в течение заранее определенного срока, равна сумме предполагаемых к получению дивидендов и ожидаемой курсовой стоимости акции в момент ее реализации, приведенная к настоящей стоимости. Таким образом, в данном случае модель определения стоимости акции аналогична соответствующей модели облигации.
Задача. Инвестор приобрел акцию и планирует держать ее в течение трех лет. Прогнозируемые дивиденды для каждого года составляют 100,150 и 200 руб. соответственно, а прогнозируемая рыночная цена через три года – 1000 руб.
Необходимо найти рыночную цену акции, если требуемая норма прибыли составляет 15%. Используя представленную выше формулу получим:
P = D1/(1+R)1+ D2/(1+R)2+ D4/(1+R)3+ Р3/(1+R)3 = 100/(1+0,15)+150/(1+0,15)2+200/(1+0,15)3+1000/(1+0,15)3 = 989,39 руб.
Ряд инвесторов при приобретении акций предполагают держать их достаточно долго. В этом случае представленное выше выражение преобразуется к виду:
P = D1/(1+R)1+ D2/(1+R)2+ … +Dn/(1+R)n = 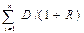i .
В представленном выражении цена акции зависит только от характера изменения дивидендов. При стабильном уровне дивидендов может быть использована рассмотренная ранее модель определения цены привилегированных акций:
P = D/R.
Задача. По акции выплачивается ежегодный постоянный дивиденд в размере 20 руб. Ожидаемая норма прибыли акции данного типа составляет 15%. При этих условиях цена акции будет равна
Р = 20 /0,15 = 133,33 руб.
Следующая модель применима к акциям дивиденд по которым характеризуется постоянным темпом роста (модель Гордона). В этом случае для цены акции используется следующее выражение:
P = D*(1+g)/(R-g).
Где D – сумма последнего выплаченного дивиденда, g – темп роста дивидендов.
Данное выражение может быть получено с использованием представленной выше формулы для определения цены акции, которая в этом случае преобразуется к виду
P = D1/(1+R)1+ D2*(1+g)/(1+R)2+ … +Dn*(1+g)n-1/(1+R)n+ Рn/(1+R)n .
Обозначим D1/(1+R) = a1, (1+g)/(1+R) = q. С учетом этого получим
P = a1+ a1*q+ … + a1*qn-1+ Рn/(1+R)n .
Первые n слагаемых данной формулы представляют собой геометрическую прогрессию. Формула для определения суммы ее n членов имеет вид
Sn = (a1-a1*qn)/(1-q).
С учетом этого выражение для определения цены акции будет иметь вид
P = D1/(R-q)*[1-(1+q)n/(1+R)n] + Pn/(1+R)n
Если рассматривать акцию как бессрочную ценную бумагу, то при неограниченном возрастании числа членов (n стремиться к бесконечности) сумма ее членов стремиться к величине
S = a1/(1-q) = D1/(R-g).
Таким образом, для расчета цены акции с постоянным темпом роста дивидендов используется соотношение
P = D1/(R-g).
Задача. Последний дивиденд, выплаченный по акции составляет 150 руб. Компания ежегодно увеличивает сумму выплачиваемых дивидендов на 10%. Ожидаемая норма доходности акций данного типа составляет 20%. При этих условиях цена акции будет равна
P = 150*(1+0,1)/(0,2-0,1) = 1650 руб.
Наиболее общей моделью оценки акций является модель переменного роста, которая позволяет учитывать различный характер роста дивидендов на различных отрезках времени. Данная модель предполагает, что после определенного момента в будущем Т дивиденды будут расти с постоянным темпом роста, а до этого времени инвестор прогнозирует индивидуальный размер выплаты дивидендов для каждого года (D1, D2, … Dn).
В рамках данной модели для определения цены акции используется следующее выражение
i
P =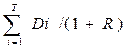 
i + Dt+1/[(R-g)*(1+R)T]
Задача. На фондовом рынке продаются акции акционерного общества «Альфа». Ожидаемые дивиденды в течение первых трех лет составляют 5 руб. на акцию. В последующие годы прогнозируются темпы прироста дивидендов — 10% в год. Требуемая норма прибыли на акцию — 20% годовых. Определить цену акции, если инвестор собирается держать акцию неограниченно долго. Для расчета цены акции в данном случае может быть использовано выражение
P = D/R*[1-1/(1+R)3] + D*(1+g)/(R-g).
P = 5/0,2*[1-1/(1+0,2)3] + 5*(1+0,1)/(0,2-0,1) = 10,53 + 55 = 65,53 руб.
Модель переменного роста величины дивидендов, описанная выше, лежит в основе многих применяемых на практике моделей дисконтирования дивидендов (DDM). Наиболее распространенные модели, называемые также трехэтапными, основаны на предположении, что компании в процессе своего развития проходят через три стадии:
1.Стадия роста характеризуется большими объемами продаж и высокими прибылями. В силу возможности высокоприбыльных инвестиций величина доли дивидендных выплат достаточно низка.
2.Переходный период характеризуется сокращением прибыли и замедлением роста доходов в результате конкуренции. В силу сокращения инвестиционных возможностей компания начинает выплачивать большую часть прибылей в виде дивидендов.
3. В стадии зрелости компания достигает состояния, при котором ее инвестиционные возможности позволяют получить лишь незначительную доходность на вложенный капитал. В этот период темпы роста доходов, доля выплат и доходность капитала стабилизируются и остаются на постоянном уровне до конца существования компании.
Процесс прогнозирования для трехэтапной DDM предполагает знание темпов роста доходов и дивидендов для всех трех фаз. Одним из самых значимых факторов, определяющих точность и соответственно эффективность применяемой модели, является качество прогноза будущих доходов и темпов роста компании. Для получения такого прогноза требуется тщательный анализ показателей финансово-хозяйственной деятельности компании. Такой анализ называется фундаментальным и охватывает не только деятельность предприятия, но и показатели экономики отрасли.
В общем случае недооцененная прибыльная, динамично растущая и прочная в финансовом положении компания представляет собой хороший объект для инвестиций. Однако абсолютные значения соответствующих показателей могут значительно различаться в зависимости от отраслевой принадлежности компании. Например, для коммунального хозяйства характерны высокая дивидендная доходность и низкие темпы роста прибыли, тогда как компании, работающие в сфере высоких технологий, могут демонстрировать стремительный рост прибыли и не выплачивать при этом вообще никаких дивидендов. Компании, зависящие от циклов деловой активности, обычно имеют более высокий уровень заемного капитала, в то время как предприятия, основывающие свою деятельность на интеллектуальной собственности, могут не нуждаться в дорогой инфраструктуре и зачастую работают либо с незначительным привлечением заемных средств, либо вообще без них.
В рамках фундаментального анализа для правильной оценки компании рассматриваются основные показатели деятельности компании, которые затем сравниваются с аналогичной группой в рамках данной отрасли. Эти показатели должны анализироваться как в абсолютных значениях — при определении стоимости акций рассматриваемой компании, так и в относительном выражении — при сравнении с другими аналогичными предприятиями.
Доходность акции
Полный доход от инвестирования в ценные бумаги складывается из текущего дохода, который получает инвестор в виде регулярных платежей процентов по облигациям и дивидендов по акциям, и курсового дохода, который образуется от изменения цены, возрастания стоимости (прирост капитала).
Для анализа эффективности вложений инвестора в покупку акций могут быть использованы следующие виды доходности: ставка дивиденда, текущая доходность акции для инвестора, текущая рыночная доходность, конечная и совокупная доходность.
Ставка дивиденда ( Rc ) определяется по формуле
Rc = D/N * 100%,
где D — величина выплачиваемых годовых дивидендов;
N — номинальная цена акции.
В российской практике ставка дивиденда обычно используется при объявлении годовых дивидендов.
Текущая доходность акции для инвестора ( Rt ) рассчитывается по формуле
Rt = D / Pp х 100%,
где Рр - цена приобретения акции.
Текущая рыночная доходность ( Rm ) определяется отношением величины выплачиваемых дивидендов к текущей рыночной цене акции (Рm):
Rm = D / Pm х 100%,
где Pm– текущая рыночная цена акции.
Конечная доходность (RK) может быть рассчитана по формуле
RK = [(Ps – Pp)/ n + D c]/ Pp х100%
где D c – величина дивидендов, выплаченная в среднем в год, n - количество лет, в течение которых инвестор владел акцией; Ps - цена продажи акции.
Доходность за период владения акцией, если она находилась у инвестора менее года, может быть определена по формуле:
R = [(Ps – Pp ) + D]/ Pp *(365/ T )
где R — доходность акции в расчете на год; Pp ,— цена покупки акции; Ps — цена продажи акции; D — дивиденды, полученные за период владения акций; Т — период владения акцией (в днях).
Задача.
Акция приобретена инвестором 1 февраля за 40 руб., продана 1 декабря того же года за 48 руб. Дивиденды в размере 3 руб. на акцию были выплачены 15 апреля. Определить доходность за период владения акцией.
С учетом того, что акция находилась у инвестора в течение 303 дней (365 - 31 - 31), имеем:
R = [(48 – 40) + 4]/ 40 *(365/303) = 0,3614 или 36,14% годовых
Однако если акция находилась у инвестора в течение нескольких лет, то данная формула дает искаженные результаты, так как здесь не учитывается стоимость денег во времени. Поэтому необходим другой подход.
Задача.
Инвестор приобрел акцию за 50 руб. и продал ее через четыре года за 84 руб. За время владения акцией инвестор получил дивиденды за первый год 3 руб., за второй год — 4 руб., за третий год — 4 руб. и за четвертый год — 5 руб. Определить доходность от операции с акцией.
Если не учитывать доходов от реинвестирования дивидендов, то после продажи акции инвестор имел на руках сумму 100 руб. (3 + 4 + 4 + 5 + 84). Таким образом, доходность за период владения акцией может быть определена по формуле
R=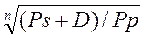 
- 1,
которая используется для определения доходности бескупонных облигаций:
R= 
- 1 0,1892 = 18,92 годовых
Однако полученный в примере результат является не совсем точным, так как не учитывает реинвестирование. Для получения более точной оценки воспользуемся методом последовательных приближений, применяя формулу, аналогичную формуле, используемой для определения цены облигаций:
Pp = D1/(1+R) + D2/(1+R)2 + D3/(1+R)3 + D4/(1+R)4 +Ps/(1+R)4
где Di —дивиденд соответствующего года; Ps — цена продажи акции; R — искомая норма прибыли; Р p — цена покупки акции.
Суть метода, как было отмечено выше, заключается в том, что мы будем придавать R различные значения, пока не получим необходимую величину Р. Расчеты показывают, что равенство приведенных денежных потоков от владения акцией и цены приобретения имеет место при R = 0,205.
Pp = 3/(1+0,205) + 4/(1+0,205)2 + 4/(1+0,205)3 + 5/(1+0,205)4 +84/(1+0,205)4 =
2,49+2,75+2,29+2,37+39,84=49.74
Полученный результат дает основание заключить, что доходность за период владения акцией составила около 20,5% годовых. Для приближенных расчетов доходности за период владения может быть использована следующая формула
RK = [(Ps – Pp)/ n + D c]/ [(Ps +Pp )/2]х100%.
RK = [(84 – 50)/ 4 + 4]/ [(84+50)/2] х100%. = 18,66 %
Оценка доходности опционов
Приведем пример валютного опциона. Ограничимся при этом позицией покупателя опциона колл.
Задача. Импортер, который имеет рубли и в будущем должен выплатить некоторую сумму в долларах США, приобретает опцион на право покупки долларов по курсу 1 долл. США = 28 рублей и выплачивает премию 0,5 рубля за 1 долл. При наступлении срока валютирования возможны следующие варианты завершения операции, определяемые движением курса доллара.
1. Курс доллара упал до 27 рублей. В этом случае покупатель не использует опцион и покупает доллары на рынке. Его результаты:
разность между курсом опциона и рыночным курсом: 28-27=1,0
премия: -0,5
условная прибыль от опциона в расчете на 1 долл.: 0,5
2. Курс доллара вырос до 29 рублей. Покупатель опциона использует свое право на покупку валюты по цене исполнения (оговоренному курсу). Результат: реальная прибыль в размере 29 - (28 + 0,5) = 0,5 рубля на 1 долл.
3. Курс равен 28. Покупатель опциона может его использовать или отказаться от него и купить валюту на рынке. В обоих случаях его расходы равны 28,5, т.е. потери относительно рыночного курса равны премии (0,5).
4.Курс превышает цену исполнения, но это превышение меньше премии. Если покупатель все же реализует опцион, то потери также меньше премии. Пусть курс равен 28,3, потери равны 28,3 - 28,5 = 0,2 на 1 долл.
Опционы представляют определенный интерес не только в практическом плане, но и в теоретическом — с позиции количественного анализа, который осуществляется с помощью разработки специальных моделей ( option models ), описывающих взаимосвязи основных параметров опционов. Следует, однако, заметить, что теоретические цены опционов, полученные по моделям, в силу неполноты учета экономических условий и их изменчивости, условности входящих статистических данных, как правило, отличаются от рыночных. Вместе с тем, принято считать, что если рыночная цена опциона сильно занижена относительно теоретической цены, то есть основание для его покупки.
Наиболее известной моделью определения цены опциона является модель Блека—Шоулза (Black—Scholes). Рассмотрим ее применительно к опционам колл для обыкновенных акций. Ранее мы говорилось о том, что цены опционов определяются на рынке и зависят от ряда известных и неизвестных на момент его покупки параметров. К их числу следует отнести:
· текущая цена базисного инструмента,
· уровень цены исполнения,
· стандартное отклонение доходности базисного инструмента,
· срок исполнения опциона,
· размер безрисковой ставки.
Все названные факторы учитываются в формуле Блека—Шоулза.
CALL = P* N(d1) – E*e-rt * N(d2)
где:
CALL — цена опциона,
P — текущая цена акции, Е — цена исполнения,
e-rt — дисконтный множитель на срок t по непрерывной ставке?
t — срок до даты исполнения,
r — непрерывная процентная ставка, принятая для дисконтирования,
N(d1) и N(d2) — функции нормального распределения,
d1 = [ln(P/E)+(r+0,5*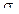 
2)*t]/( 
√ t),
d2 = d1 - 
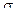√ t
Величина E*e-rt представляет собой дисконтированную на момент покупки опциона цену исполнения. Функции нормального распределения (плотности вероятности) определяются для параметров d 1 и d 2 .
Задача. Колл опцион дает право на приобретение акций компании А по цене 20 рублей за штуку. До срока исполнения остается 0,5 года. Безрисковая ставка равна 5% и стандартное отклонение доходности акций составляет 0,3. Стоимость акций в настоящее время составляет 25 рублей за штуку. Необходимо определить цену опциона.
Шаг 1. Рассчитываем значения величин d 1 и d 2.
d1 = [ln(P/E)+(r+0,5*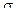 
2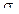)*t]/( √ t),
d1 = [ln(25/20)+(0,05+0,5*0,045)*0,5]/(0,3√ 0,5),
d1 = [0,22314+0,095*0,5]/0,2121
d1 = 1,276.
d2 = d1 - 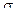√ t
d2 = 1,276 – 0,3 * √ 0,5
d2 = 1,064.
Шаг 2. Рассчитываем значения N(d1) и N(d2). Величины N(d1) и N(d2) находим по таблице нормального распределения или рассчитываем при помощи Exel. В нашем примере
N(d1) = 0,899,
N(d2).= 0,8563.
Шаг 3 Рассчитываем стоимость опциона
CALL = P* N(d1) – E*e-rt * N(d2)
CALL = 25* 0,899 – 20*e-0,05*0,5 * 0,8563 = 5,77.
Задача.
4 октября 200 г. цена закрытия опциона компании Х со сроком исполнения 21 апреля 2001 г. и ценой исполнения $49 составила $4. Базовые акции продаются по цене $50. 4 октября срок до исполнения составляет 199 дней. Непрерывно начисляемая безрисковая ставка равна 7%. Дисперсия доходности акций составляет 0,09.
Шаг 1. . Рассчитываем значения величин d 1 и d 2.
d1 = [ln(P/E)+(r+0,5* 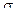2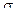)*t]/( √ t),
d1 = [ln(50/49)+(0,07+0,5*0,09)*199/365]/(√0,09*199/365) = 0,3742
d2 = d1 - 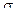√ t
d2 = 0,3742 - √0,09*199/365 = 0,1527.
Шаг 2. Рассчитываем значения N(d1) и N(d2).
Величины N(d1) и N(d2) находим по таблице нормального распределения или рассчитываем при помощи Exel. В нашем примере N(d1) = 0,6459 и N(d2) = 0,5607
Шаг 3 Рассчитываем стоимость опциона
CALL = P* N(d1) – E*e-rt * N(d2)
CALL = 50* 0,6459 – 49*e-0,07*199/365 * 0,5607= 5,85.
Таким образом, цена опциона, полученная с помощью модели Блэка-Шоулза оказалась выше, чем цена на рынке. Это означает, что опцион недооценен и для инвестора целесообразно приобретение данного опциона.
Дата: 2019-02-25, просмотров: 159.
