Цена купонной облигации.
Задача. Продается облигация номиналом 10000 руб. Процентная (купонная) ставка составляет 12% годовых. Выплата процентов производится один раз в год. До погашения облигации остается ровно 5 лет. Требуемая норма прибыли (доходность инвестиции с учетом риска, соответствующего данному типу облигаций, составляет 15%).
Определите курсовую цену облигации.
Решение
В конце каждого года держатель облигации получит процентный доход в размере 1200 руб., а в конце пятого года — еще и сумму, равную номиналу облигации т. е. 10000 руб. Определим дисконтированные (приведенные) стоимости для каждого года и найдем их сумму.
Приведенная стоимость платежей составит:
первый год = 1200/(1+0,15)1 =1043,48 руб.
второй год = 1200/(1+0,15)2 = 907,37 руб.
третий год = 1200/(1+0,15)3 = 789,02 руб.
четвертый год = 1200/(1+0,15)4 = 686,10 руб.
пятый год = (1200+10000)/(1+0,15)5 = 5568,38 руб.
Таким образом, искомая цена облигации будет равна:
1043,48+ 907,37 + 789,02 + 686,1 + 5568,38 = 8994,35 руб.
Часто цена облигации выражается в процентном отношении к номиналу. Применительно к приведенному примеру цена облигации составляет 89,94% номинала.
Формула для определения стоимости облигации может быть представлена в следующем общем виде
P = I/(1+R)1+ I/(1+R)2+ … +I/(1+R)n+ N/(1+R)n = 
i + N/(1+R)n
где
Р — цена облигации; I — процентный (купонный) доход в денежных единицах, R — требуемая норма прибыли (ставка дисконтирования).
Для расчета цены облигации может быть использована полученная ранее формула аннуитета
P = I/R*[1-1/(1+R)n] + N/(1+R)n.
Для приведенного выше примера цена облигации, вычисленная по полученной формуле, составит:
P = 1200/0,15*[1-1/(1+0,15)5] + 10000/(1+0,15)5 = 8994,35 руб.
Таким образом, мы получили тот же результат, что ив предыдущем случае. Приведенные выше расчеты справедливы, если ставка дисконтирования (требуемая норма прибыли) остается неизменной в течение рассматриваемого периода (срока действия облигации). В действительности ставка может изменяться. В этом случае для определения стоимости облигаций требуется найти дисконтированные потоки доходов для каждого года, используя следующую формулу:
Dpi = Di/[(1+R1)*(1+R2) )*… *(1+Ri)]
где Dpi— приведенная стоимость дохода i-ого года; Di – доход i-того года; R1, R2, Ri — ставка дисконтирования для 1-го, 2-го, ..., i -го года.
Задача. По облигации номиналом 10000 руб. выплачивается доход в размере 10% годовых. Выплата процентов производится один раз в год. До погашения облигации остается 5 лет. Требуемая норма прибыли в течение первых трех лет — 15%, четвертый год — 12, пятый год — 10%.
Определить курсовую цену облигации.
В данном примере процентный доход каждого года и сумму погашения облигации необходимо продисконтировать по переменной ставке. Определим дисконтированные стоимости для платежей каждого года:
первый год = 1000/(1+0,15)1 = 869,57 руб.
второй год = 1000/(1+0,15)2 = 756,14 руб.
третий год = 1000/(1+0,15)3 = 657,52 руб.
четвертый год = 1000/[(1+0,15)3 * (1+0,12)] = 587,07 руб.
пятый год = (1000+10000)/[(1+0,15)3 * (1+0,12) * (1+0,1)] = 5870,68 руб.
Следовательно, цена облигации составит:
Р = 869,57+ 756,14 + 657,52 + 587,07 + 5870,68 =8740,98 руб.
Мы видим, что стоимость облигации выше, чем в предыдущем случае, так ставка дисконтирования в четвертом и пятом годах ниже, чем в первые три года.
Мы рассмотрели вопрос определения цены облигации при ежегодных купонных выплатах. На практике процентные платежи могут осуществляться чаще, чем один раз в год. Так, например, по облигациям, эмитированным в США, доход часто выплачивается два раза в год. Для определения цены таких облигаций может быть использовано выражение
P = (I/m)/(R/m)*[1-1/(1+(R/m))n] + N/(1+(R/m))n*m ,
где m – число купонных выплат в течение года.
Задача. По облигации, имеющей номинальную цену 1000 рублей и купонную ставку 14%, процентные платежи выплачиваются два раза в год. Необходимо определить цену облигации, если до погашения остается 7 лет и требуемая норма прибыли составляет 16% годовых. Используя представленную выше формулу получим
P = (I/m)/(R/m)*[1-1/(1+(R/m))n] + N/(1+(R/m))n*m =
70/0,08*[1-1/(1+0,0814 ]+ 1000/(1+0,0814) = 917,56 руб.
Для облигаций, купонные выплаты по которым осуществляются чаще, чем один раз в год может быть рассчитана эффективная процентная ставка с использованием следующего выражения:
iэ = (1+i/m)m -1.
Для предыдущего примера эффективная купонная ставка будет равна
iэ = (1+i/ m)m -1 = (1+0,14/2)2 -1 = 0,145 или 14,5%.
Доходность облигаций
Облигации приобретаются инвесторами с целью получение дохода. Для анализа эффективности вложений в разные виды облигаций, а также в другие ценные бумаги следует сопоставить величину получаемого дохода с величиной инвестиций с затратами на приобретение ценной бумаги. Различают следующие показатели доходности: купонная доходность, текущая доходность, доходность к погашению, доходность за период владения.
Купонная доходность (RК) устанавливается при выпуске облигации и для ее расчета используется следующая формула:
RК=I/N,
Где
I — купонный доход, N— номинальная цена облигации.
Текущая доходность (RT) определяется как отношение величины процентного дохода к цене приобретения облигации:
RT= I /P,
где
I — процентный доход,
Р — цена приобретения облигации.
Задача. Облигация номиналом 1000 руб. продается по цене 900 руб. процентный доход в размере 15% годовых выплачивается один раз в год. Определить купонную и текущую доходность облигации.
Купонная доходность будет равна:
RК=I/N = 150/1000 = 0,15 или 15% годовых
Текущая доходность будет равна:
RT= I /P = 150/900 = 0,167 или 16,7% годовых.
Доходность к погашению равна требуемой норме прибыли инвестора R, при которой приведенная стоимость денежных платежей по облигации равна ее рыночной стоимости. В течение срока жизни облигации происходит изменение ее рыночной цены и доходности вследствие изменения процентных ставок. Если инвестор собирается держать облигацию до погашения, то он может сопоставить все полученные по облигации доходы (процентные платежи и сумму погашения) с ценой приобретения облигации. Полученная таким способом величина называется доходностью к погашению или внутренней нормой прибыли.
Доходность к погашению можно определить методом последовательных приближений, используя полученную ранее формулу
P = I/R*[1-1/(1+R)n] + N/(1+R)n,
где
P – рыночная цена облигации,
R – доходность к погашению,
n – число периодов владения облигацией.
Метод последовательных приближений реализуется путем подстановки в данную формулу различные значения R и определения для каждого значения R соответствующего значения цены. Если для выбранного значения R мы получаем цену выше заданного значения цены (Р), то следует увеличить значение R и найти новое значение Р. Если получено значение Р ниже заданной цены, то необходимо уменьшить значение R. Такие действия необходимо продолжать до тех пор, пока расчетная цена не совпадет с заданной точностью с рыночной ценой. Полученное таким образом значение R и будет являться доходностью облигации к погашению или внутренней нормой прибыли облигации.
Задача. Номинал облигации — 1000 руб. Срок погашения облигации — через 3 года. По облигации выплачивается 15% годовых, выплата производится один раз в год. Курсовая цена облигации — 920 руб. Определить доходность облигации к погашению. В качестве первого приближения возьмем ставку дисконтирования равной 17%. Найдем цену облигации:
P = 150/0,17*[1-1/(1+0,17)3] + 1000/(1+0,17)3 = 955,81 руб.
Мы получим цену, которая выше курсовой цены облигации. Следовательно, ставка дисконтирования должна быть увеличена. Увеличим ее до 19% и найдем новое значение цены облигации:
P = 150/0,19*[1-1/(1+0,19)3] + 1000/(1+0,19)3 == 914,4 руб.
Мы получили значение цены, которое ниже курсовой цены облигации. Следовательно, чтобы получить значение цены, равное курсовой стоимости облигации ставка дисконтирования должна быть ниже 19%. Искомое значение находится между 17% и 19%. Продолжая представленные расчеты, можно найти значение доходности к погашению – 18,7%. Цена облигации в этом случае будет равна
P = 150/0,187*[1-1/(1+0,187)3] + 1000/(1+0,187)3 = 920,45 руб.
Таким образом, при ставке дисконтирования равной 18,7% текущая стоимость процентных платежей и суммы погашения облигации равна покупной цене облигации – затратам инвестора. Это означает, что доходность облигации к погашению составляет 18,7%. Использование показателя доходности к погашению позволяет инвестору решить вопрос о приемлемости инвестиций в приобретение облигации.
В реальных ситуациях для принятия того или иного решения не всегда необходимо производить точные вычисления, так как многие факторы, определяющие доходность финансовых инструментов, остаются вне контроля инвестора. В этом случае для получения приблизительного результата можно использовать следующую формулу:
R = [(N-P)/n+I]/[(N+P)/2],
где
N — номинал облигации;
Р— цена облигации;
п — число лет до погашения облигации;
I — ежегодный процентный доход.
Для приведенного выше Примера имеем:
R = [(1000-920)/3+150]/[(1000+920)/2] = 18,4%.
Отклонение значения доходности, полученного с помощью приближенной формулы, весьма незначительно и находится в пределах допустимой ошибки.
Бескупонная облигация
Для определения доходности бескупонной облигации (облигации с нулевым купоном) необходимо воспользоваться формулой для определения цены облигации:
P = N/(1+R)n.
После преобразований получаем следующее выражение для доходности бескупонной облигации:
R=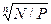 
- 1
Задача. Определить доходность бескупонной облигации номинальной стоимостью 1000 руб. Рыночная цена облигации равна 700 руб. и до погашения остается 3 года. Доходность определяется из представленного выше выражения
R= 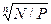- 1 =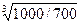 
- 1 = 0,126 или же 12,6%.
Доходность краткосрочных облигаций (сроком действия до 1 года) обычно определяется по формуле:
R = (DI/P) * (365/T)
где DI — величина дисконта; Р –цена облигации; Т — число дней до погашения облигации. Подставляя вместо D = N-Р, получаем:
R = [(N-P)/P] * (365/T) = (N/P-1)*(365/T)
Задача. Облигация номиналом 1000 руб. продается с дисконтом по цене 950 рублей. До погашения облигации остается 60 дней. Определить доходность к погашению. Используя полученное выше выражение получаем:
R = (1000/950-1)*(365/60) = 0,320 или же 32,0%
Доходность акции
Полный доход от инвестирования в ценные бумаги складывается из текущего дохода, который получает инвестор в виде регулярных платежей процентов по облигациям и дивидендов по акциям, и курсового дохода, который образуется от изменения цены, возрастания стоимости (прирост капитала).
Для анализа эффективности вложений инвестора в покупку акций могут быть использованы следующие виды доходности: ставка дивиденда, текущая доходность акции для инвестора, текущая рыночная доходность, конечная и совокупная доходность.
Ставка дивиденда ( Rc ) определяется по формуле
Rc = D/N * 100%,
где D — величина выплачиваемых годовых дивидендов;
N — номинальная цена акции.
В российской практике ставка дивиденда обычно используется при объявлении годовых дивидендов.
Текущая доходность акции для инвестора ( Rt ) рассчитывается по формуле
Rt = D / Pp х 100%,
где Рр - цена приобретения акции.
Текущая рыночная доходность ( Rm ) определяется отношением величины выплачиваемых дивидендов к текущей рыночной цене акции (Рm):
Rm = D / Pm х 100%,
где Pm– текущая рыночная цена акции.
Конечная доходность (RK) может быть рассчитана по формуле
RK = [(Ps – Pp)/ n + D c]/ Pp х100%
где D c – величина дивидендов, выплаченная в среднем в год, n - количество лет, в течение которых инвестор владел акцией; Ps - цена продажи акции.
Доходность за период владения акцией, если она находилась у инвестора менее года, может быть определена по формуле:
R = [(Ps – Pp ) + D]/ Pp *(365/ T )
где R — доходность акции в расчете на год; Pp ,— цена покупки акции; Ps — цена продажи акции; D — дивиденды, полученные за период владения акций; Т — период владения акцией (в днях).
Задача.
Акция приобретена инвестором 1 февраля за 40 руб., продана 1 декабря того же года за 48 руб. Дивиденды в размере 3 руб. на акцию были выплачены 15 апреля. Определить доходность за период владения акцией.
С учетом того, что акция находилась у инвестора в течение 303 дней (365 - 31 - 31), имеем:
R = [(48 – 40) + 4]/ 40 *(365/303) = 0,3614 или 36,14% годовых
Однако если акция находилась у инвестора в течение нескольких лет, то данная формула дает искаженные результаты, так как здесь не учитывается стоимость денег во времени. Поэтому необходим другой подход.
Задача.
Инвестор приобрел акцию за 50 руб. и продал ее через четыре года за 84 руб. За время владения акцией инвестор получил дивиденды за первый год 3 руб., за второй год — 4 руб., за третий год — 4 руб. и за четвертый год — 5 руб. Определить доходность от операции с акцией.
Если не учитывать доходов от реинвестирования дивидендов, то после продажи акции инвестор имел на руках сумму 100 руб. (3 + 4 + 4 + 5 + 84). Таким образом, доходность за период владения акцией может быть определена по формуле
R=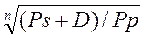 
- 1,
которая используется для определения доходности бескупонных облигаций:
R= 
- 1 0,1892 = 18,92 годовых
Однако полученный в примере результат является не совсем точным, так как не учитывает реинвестирование. Для получения более точной оценки воспользуемся методом последовательных приближений, применяя формулу, аналогичную формуле, используемой для определения цены облигаций:
Pp = D1/(1+R) + D2/(1+R)2 + D3/(1+R)3 + D4/(1+R)4 +Ps/(1+R)4
где Di —дивиденд соответствующего года; Ps — цена продажи акции; R — искомая норма прибыли; Р p — цена покупки акции.
Суть метода, как было отмечено выше, заключается в том, что мы будем придавать R различные значения, пока не получим необходимую величину Р. Расчеты показывают, что равенство приведенных денежных потоков от владения акцией и цены приобретения имеет место при R = 0,205.
Pp = 3/(1+0,205) + 4/(1+0,205)2 + 4/(1+0,205)3 + 5/(1+0,205)4 +84/(1+0,205)4 =
2,49+2,75+2,29+2,37+39,84=49.74
Полученный результат дает основание заключить, что доходность за период владения акцией составила около 20,5% годовых. Для приближенных расчетов доходности за период владения может быть использована следующая формула
RK = [(Ps – Pp)/ n + D c]/ [(Ps +Pp )/2]х100%.
RK = [(84 – 50)/ 4 + 4]/ [(84+50)/2] х100%. = 18,66 %
Оценка доходности опционов
Приведем пример валютного опциона. Ограничимся при этом позицией покупателя опциона колл.
Задача. Импортер, который имеет рубли и в будущем должен выплатить некоторую сумму в долларах США, приобретает опцион на право покупки долларов по курсу 1 долл. США = 28 рублей и выплачивает премию 0,5 рубля за 1 долл. При наступлении срока валютирования возможны следующие варианты завершения операции, определяемые движением курса доллара.
1. Курс доллара упал до 27 рублей. В этом случае покупатель не использует опцион и покупает доллары на рынке. Его результаты:
разность между курсом опциона и рыночным курсом: 28-27=1,0
премия: -0,5
условная прибыль от опциона в расчете на 1 долл.: 0,5
2. Курс доллара вырос до 29 рублей. Покупатель опциона использует свое право на покупку валюты по цене исполнения (оговоренному курсу). Результат: реальная прибыль в размере 29 - (28 + 0,5) = 0,5 рубля на 1 долл.
3. Курс равен 28. Покупатель опциона может его использовать или отказаться от него и купить валюту на рынке. В обоих случаях его расходы равны 28,5, т.е. потери относительно рыночного курса равны премии (0,5).
4.Курс превышает цену исполнения, но это превышение меньше премии. Если покупатель все же реализует опцион, то потери также меньше премии. Пусть курс равен 28,3, потери равны 28,3 - 28,5 = 0,2 на 1 долл.
Опционы представляют определенный интерес не только в практическом плане, но и в теоретическом — с позиции количественного анализа, который осуществляется с помощью разработки специальных моделей ( option models ), описывающих взаимосвязи основных параметров опционов. Следует, однако, заметить, что теоретические цены опционов, полученные по моделям, в силу неполноты учета экономических условий и их изменчивости, условности входящих статистических данных, как правило, отличаются от рыночных. Вместе с тем, принято считать, что если рыночная цена опциона сильно занижена относительно теоретической цены, то есть основание для его покупки.
Наиболее известной моделью определения цены опциона является модель Блека—Шоулза (Black—Scholes). Рассмотрим ее применительно к опционам колл для обыкновенных акций. Ранее мы говорилось о том, что цены опционов определяются на рынке и зависят от ряда известных и неизвестных на момент его покупки параметров. К их числу следует отнести:
· текущая цена базисного инструмента,
· уровень цены исполнения,
· стандартное отклонение доходности базисного инструмента,
· срок исполнения опциона,
· размер безрисковой ставки.
Все названные факторы учитываются в формуле Блека—Шоулза.
CALL = P* N(d1) – E*e-rt * N(d2)
где:
CALL — цена опциона,
P — текущая цена акции, Е — цена исполнения,
e-rt — дисконтный множитель на срок t по непрерывной ставке?
t — срок до даты исполнения,
r — непрерывная процентная ставка, принятая для дисконтирования,
N(d1) и N(d2) — функции нормального распределения,
d1 = [ln(P/E)+(r+0,5*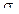 
2)*t]/( 
√ t),
d2 = d1 - 
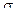√ t
Величина E*e-rt представляет собой дисконтированную на момент покупки опциона цену исполнения. Функции нормального распределения (плотности вероятности) определяются для параметров d 1 и d 2 .
Задача. Колл опцион дает право на приобретение акций компании А по цене 20 рублей за штуку. До срока исполнения остается 0,5 года. Безрисковая ставка равна 5% и стандартное отклонение доходности акций составляет 0,3. Стоимость акций в настоящее время составляет 25 рублей за штуку. Необходимо определить цену опциона.
Шаг 1. Рассчитываем значения величин d 1 и d 2.
d1 = [ln(P/E)+(r+0,5*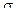 
2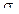)*t]/( √ t),
d1 = [ln(25/20)+(0,05+0,5*0,045)*0,5]/(0,3√ 0,5),
d1 = [0,22314+0,095*0,5]/0,2121
d1 = 1,276.
d2 = d1 - 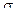√ t
d2 = 1,276 – 0,3 * √ 0,5
d2 = 1,064.
Шаг 2. Рассчитываем значения N(d1) и N(d2). Величины N(d1) и N(d2) находим по таблице нормального распределения или рассчитываем при помощи Exel. В нашем примере
N(d1) = 0,899,
N(d2).= 0,8563.
Шаг 3 Рассчитываем стоимость опциона
CALL = P* N(d1) – E*e-rt * N(d2)
CALL = 25* 0,899 – 20*e-0,05*0,5 * 0,8563 = 5,77.
Задача.
4 октября 200 г. цена закрытия опциона компании Х со сроком исполнения 21 апреля 2001 г. и ценой исполнения $49 составила $4. Базовые акции продаются по цене $50. 4 октября срок до исполнения составляет 199 дней. Непрерывно начисляемая безрисковая ставка равна 7%. Дисперсия доходности акций составляет 0,09.
Шаг 1. . Рассчитываем значения величин d 1 и d 2.
d1 = [ln(P/E)+(r+0,5* 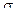2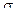)*t]/( √ t),
d1 = [ln(50/49)+(0,07+0,5*0,09)*199/365]/(√0,09*199/365) = 0,3742
d2 = d1 - 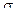√ t
d2 = 0,3742 - √0,09*199/365 = 0,1527.
Шаг 2. Рассчитываем значения N(d1) и N(d2).
Величины N(d1) и N(d2) находим по таблице нормального распределения или рассчитываем при помощи Exel. В нашем примере N(d1) = 0,6459 и N(d2) = 0,5607
Шаг 3 Рассчитываем стоимость опциона
CALL = P* N(d1) – E*e-rt * N(d2)
CALL = 50* 0,6459 – 49*e-0,07*199/365 * 0,5607= 5,85.
Таким образом, цена опциона, полученная с помощью модели Блэка-Шоулза оказалась выше, чем цена на рынке. Это означает, что опцион недооценен и для инвестора целесообразно приобретение данного опциона.
Цена купонной облигации.
Задача. Продается облигация номиналом 10000 руб. Процентная (купонная) ставка составляет 12% годовых. Выплата процентов производится один раз в год. До погашения облигации остается ровно 5 лет. Требуемая норма прибыли (доходность инвестиции с учетом риска, соответствующего данному типу облигаций, составляет 15%).
Определите курсовую цену облигации.
Решение
В конце каждого года держатель облигации получит процентный доход в размере 1200 руб., а в конце пятого года — еще и сумму, равную номиналу облигации т. е. 10000 руб. Определим дисконтированные (приведенные) стоимости для каждого года и найдем их сумму.
Приведенная стоимость платежей составит:
первый год = 1200/(1+0,15)1 =1043,48 руб.
второй год = 1200/(1+0,15)2 = 907,37 руб.
третий год = 1200/(1+0,15)3 = 789,02 руб.
четвертый год = 1200/(1+0,15)4 = 686,10 руб.
пятый год = (1200+10000)/(1+0,15)5 = 5568,38 руб.
Таким образом, искомая цена облигации будет равна:
1043,48+ 907,37 + 789,02 + 686,1 + 5568,38 = 8994,35 руб.
Часто цена облигации выражается в процентном отношении к номиналу. Применительно к приведенному примеру цена облигации составляет 89,94% номинала.
Формула для определения стоимости облигации может быть представлена в следующем общем виде
P = I/(1+R)1+ I/(1+R)2+ … +I/(1+R)n+ N/(1+R)n = i + N/(1+R)n
где
Р — цена облигации; I — процентный (купонный) доход в денежных единицах, R — требуемая норма прибыли (ставка дисконтирования).
Для расчета цены облигации может быть использована полученная ранее формула аннуитета
P = I/R*[1-1/(1+R)n] + N/(1+R)n.
Для приведенного выше примера цена облигации, вычисленная по полученной формуле, составит:
P = 1200/0,15*[1-1/(1+0,15)5] + 10000/(1+0,15)5 = 8994,35 руб.
Таким образом, мы получили тот же результат, что ив предыдущем случае. Приведенные выше расчеты справедливы, если ставка дисконтирования (требуемая норма прибыли) остается неизменной в течение рассматриваемого периода (срока действия облигации). В действительности ставка может изменяться. В этом случае для определения стоимости облигаций требуется найти дисконтированные потоки доходов для каждого года, используя следующую формулу:
Dpi = Di/[(1+R1)*(1+R2) )*… *(1+Ri)]
где Dpi— приведенная стоимость дохода i-ого года; Di – доход i-того года; R1, R2, Ri — ставка дисконтирования для 1-го, 2-го, ..., i -го года.
Задача. По облигации номиналом 10000 руб. выплачивается доход в размере 10% годовых. Выплата процентов производится один раз в год. До погашения облигации остается 5 лет. Требуемая норма прибыли в течение первых трех лет — 15%, четвертый год — 12, пятый год — 10%.
Определить курсовую цену облигации.
В данном примере процентный доход каждого года и сумму погашения облигации необходимо продисконтировать по переменной ставке. Определим дисконтированные стоимости для платежей каждого года:
первый год = 1000/(1+0,15)1 = 869,57 руб.
второй год = 1000/(1+0,15)2 = 756,14 руб.
третий год = 1000/(1+0,15)3 = 657,52 руб.
четвертый год = 1000/[(1+0,15)3 * (1+0,12)] = 587,07 руб.
пятый год = (1000+10000)/[(1+0,15)3 * (1+0,12) * (1+0,1)] = 5870,68 руб.
Следовательно, цена облигации составит:
Р = 869,57+ 756,14 + 657,52 + 587,07 + 5870,68 =8740,98 руб.
Мы видим, что стоимость облигации выше, чем в предыдущем случае, так ставка дисконтирования в четвертом и пятом годах ниже, чем в первые три года.
Мы рассмотрели вопрос определения цены облигации при ежегодных купонных выплатах. На практике процентные платежи могут осуществляться чаще, чем один раз в год. Так, например, по облигациям, эмитированным в США, доход часто выплачивается два раза в год. Для определения цены таких облигаций может быть использовано выражение
P = (I/m)/(R/m)*[1-1/(1+(R/m))n] + N/(1+(R/m))n*m ,
где m – число купонных выплат в течение года.
Задача. По облигации, имеющей номинальную цену 1000 рублей и купонную ставку 14%, процентные платежи выплачиваются два раза в год. Необходимо определить цену облигации, если до погашения остается 7 лет и требуемая норма прибыли составляет 16% годовых. Используя представленную выше формулу получим
P = (I/m)/(R/m)*[1-1/(1+(R/m))n] + N/(1+(R/m))n*m =
70/0,08*[1-1/(1+0,0814 ]+ 1000/(1+0,0814) = 917,56 руб.
Для облигаций, купонные выплаты по которым осуществляются чаще, чем один раз в год может быть рассчитана эффективная процентная ставка с использованием следующего выражения:
iэ = (1+i/m)m -1.
Для предыдущего примера эффективная купонная ставка будет равна
iэ = (1+i/ m)m -1 = (1+0,14/2)2 -1 = 0,145 или 14,5%.
Зависимость цены облигации от процентной ставки
Рассмотрим зависимость цены облигации от ставки процента (требуемой нормы прибыли R). Цена облигации складывается из дисконтированных купонных выплат и номинала облигации. Из представленной ниже формулы видно, что обе эти величины убывают при повышении процентной ставки R. Исходя из этого, мы можем сделать вывод о влиянии денежно-кредитной политики государства на рыночные цены облигаций.
P = D/R*[1-1/(1+R)n] + N/(1+R)n.
При повышении учетной ставки ЦБ происходит повышение стоимости денежно-кредитных ресурсов в экономике – растут процентные ставки. Соответственно повышаются требования инвесторов к доходности облигаций. Новые облигации эмитируются с большей величиной доходности, а стоимость ранее эмитированных облигаций понижается для обеспечения повысившихся требований к доходности. При снижении учетной ставки ситуации развивается в противоположном направлении.
Задача. Облигация имеет номинал 10000 рублей, купонную ставку 6% и срок погашения 15 лет. Определить размер премии (дисконта), если требуемая норма прибыли составляет 8%.
Найдем цену облигации с использованием следующего выражения
P = D/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,08*[1-1/(1+0,08)15] + 10000/(1+0,08)15 =
5135,7 + 3152,4 = 8288,1.
Таким образом, в данном случае облигация продается с дисконтом размер которого составляет 10000 – 8288,1 = 1711,9 руб.
Рассмотрим далее случай, когда требуемая норма прибыли меньше купонной ставки, R = 4%.
P = D/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,04*[1-1/(1+0,04)15] + 10000/(1+0,04)15 =
6671 + 5553 = 12224.
В данном случае облигация продается с премией, размер которой составляет 2224 руб.
Последний вариант соответствует равенству купонной ставки и нормы прибыли
P = D/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,06*[1-1/(1+0,06)15] + 10000/(1+0,06)15 =
5827 + 4173 = 10000 руб.
Таким образом, мы можем сделать вывод, что при равенстве требуемой нормы прибыли и купонной ставки курсовая цена облигации равна ее номиналу. При превышении нормы прибыли купонной ставки облигация продается с дисконтом, а при понижении относительно купонной ставки – с премией. Цена облигации и требуемая норма прибыли связаны обратной зависимостью. При повышении процентной ставки цена облигации, которая определяется как приведенная стоимость будущих денежных поступлений, падает; при снижении ставок ситуации развивается в противоположном направлении.
Рассмотрим далее влияние фактора времени на стоимость облигации. В предыдущем примере рассмотрим эффект уменьшения срока погашения облигации до 10 лет:
P = D/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,08*[1-1/(1+0,08)10] + 10000/(1+0,08)10 =
4026 + 4632 = 8658 руб.
P = D/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,04*[1-1/(1+0,04)10] + 10000/(1+0,04)10 =
4867 + 6756 = 11623 руб.
P = D/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,06*[1-1/(1+0,06)10] + 10000/(1+0,06)10 =
4416 + 5584 = 1000 руб.
На основе проделанных вычислений мы можем сделать вывод, что при уменьшении срока погашения облигации произошло снижение размера дисконта и премии. При равенстве купонной ставки и нормы прибыли курсовая цена равна номиналу вне зависимости от срока погашения.
Теперь рассмотрим эффект увеличения срока погашения до 20 лет:
P = D/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,08*[1-1/(1+0,08)20] + 10000/(1+0,08)20 =
5891 + 2146 = 8037 руб.
P = D/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,04*[1-1/(1+0,04)20] + 10000/(1+0,04)20 =
8154 + 4564 = 12718 руб.
Как и следовало ожидать, при увеличении срока погашения происходит возрастание как величины дисконта, так и премии.
Зависимость цены облигаций от процентной ставки обуславливает риск инвесторов, связанный с ее колебаниями. В связи с этим актуальной является задача анализа чувствительности цены облигации к изменению требуемой нормы прибыли. Выражение для цены облигации может быть представлено в следующем виде:
P = CF1/(1+R)1+ CF2/(1+R)2+ … + CF n/(1+R)n,
где
CF i – доход инвестора от владения облигацией в соответствующий период. Для анализа чувствительности цены к процентной ставке необходимо вычислить производную цены по доходности:
dP/dR = (-1)*CF1/(1+R)2+ (-2)*CF2/(1+R)3+ … + (-n)*CF n/(1+R)n+1,
Разделим далее левую и правую части соотношения на цену облигации (Р):
dP/dR * 1/Р= [(-1)*CF1/(1+R)2+ (-2)*CF2/(1+R)3+ … + (-n)*CF n/(1+R)n+1]/P.
Таким образом, мы получили выражение нормализованной по цене облигации чувствительности цены к изменению нормы прибыли. Представленное ниже выражение определяет показатель «дюрации» облигации (D)
D= [(1)*CF1/(1+R)2+ (2)*CF2/(1+R)3+ … + (n)*CF n/(1+R)n+1]/P.
Дюрация характеризует процентный риск облигации, т.е.е риск, связанный с изменением процентных ставок. При увеличении значения дюрации возрастает чувствительность цены облигации к изменению процентной ставки и соответственно увеличивается риск ценной бумаги.
Задача. Необходимо рассчитать дюрацию облигации, имеющей номинальную цену 1000 руб., купонную ставку 10% и срок погашения 5 лет. Результаты расчетов сведены в таблицу
Таблица
Расчет дюрации облигации
| Номер платежа | Размер платежа CF i | Приведенная величина платежа CF i/(1+R) i | Нормализованная приведенная величина платежа CF i/(1+R) i/Р | Величина i * CF i/(1+R) i/Р |
| 1 | 100 | 90,91 | 0,09091 | 0,9091 |
| 2 | 100 | 82,64 | 0,08264 | 0,16528 |
| 3 | 100 | 75,13 | 0,07513 | 0,22539 |
| 4 | 100 | 68,3 | 0,06830 | 0,27320 |
| 5 | 1100 | 683,02 | 0,68302 | 3,41510 |
| Итого | 1000 | 1,0 | 4,1699 | |
Таким образом, величина дюрации для анализируемой облигации составила 4,1699 лет. Дюрацию называют также эффективным сроком жизни облигации. Чем выше этот срок жизни, тем в большей мере облигация реагирует на изменение процентных ставок; иными словами тем она более чувствительна к изменению ставок.
В общем случае чувствительность цены к изменению процентных ставок зависит от времени до погашения облигации и купонной ставки; величина процентного риска возрастает при увеличении времени до погашения и снижении купонной ставки. Обусловлено это тем обстоятельством, что существенная часть цены облигации формируется за счет вклада приведенного значения номинальной цены, которую инвестор получает при погашении облигации. Чем дальше от текущего момента осуществляется эта выплата, тем она больше зависит от изменения процентной ставки. Что касается величины купонной ставки, то ситуация здесь примерно аналогична предыдущему случаю. При снижении купонной ставки повышается та часть цены облигации, которая формируется за счет приведенного значения номинальной цены, что, как было показано выше, приводит к росту процентного риска.
До сих пор мы рассматривали случаи, когда до погашения облигации остается целое число лет или купонных периодов. Однако облигации могут продаваться и покупаются в любой момент времени (в начале, середине и в конце купонного периода). Допустим, облигация, о которой шла речь в Примере 1, продается не за 5 лет до погашения, а за 4 года и 300 дней до срока погашения. Покупатель получит годовой процентный доход по этой облигации (при условии выплаты процентов 1 раз в год) через 300 дней после покупки облигации. Между тем в течение 65 дней облигация находилась в руках продавца, которому по праву принадлежит процентный доход за этот период, в то время как покупателю причитается доход только за 300 дней. Процентный доход покупателя и продавца за время Т определяется по формуле:
Dr = D * T/365.
где
D — процентный доход за год или купонный период;
Т — время, в течение которого облигация находилась в руках продавца или покупателя (в днях);
Dr — процентный доход за время Т.
В нашем Примере процентный доход покупателя составит:
D300 = 1200 * 300/365 = 986,3 руб.
Процентный доход продавца будет равен:
D65 = 1200 * 65/365 = 213,7 руб.
Поскольку процентный доход в размере 213,7 руб., принадлежащий продавцу, получит покупатель облигации при оплате очередного купона, то цена облигации должна быть увеличена таким образом, чтобы продавец не понес ущерба. В рассматриваемом нами случае цена (цена, вычисленная в Примере 1) должна быть увеличена на 213,7 руб. и составить 8954,68 руб.
Однако это лишь приблизительный результат, так как цена в размере 850,47 руб. была получена нами при дисконтировании доходов ровно за 5 лет. Поэтому чтобы получить более точный результат, нужно продисконтировать ожидаемые доходы за тот период времени, который остается до погашения облигации с момента совершения сделки.
Определим цену облигации для нашего примера:
P = 1200/(1+0,15)300/365+ 1200/(1+0,15)1+300/365+1200/(1+0,15)2+300/365 1200/(1+0,15)3+300/365 (1200+10000)/(1+0,15)4+300/365 = 1021,83+ 930,23+808,89+703,39+ 5708,64 = 9172,98 руб.
Выше речь шла об облигациях с постоянным купоном. Однако купонные облигации могут быть как с постоянной, так и переменной купонной ставкой. Изменения характеризуются тем, что величина процентного дохода изменяется в зависимости от изменения ситуации на финансовом рынке. Стоимость таких облигаций определяется по формуле:
P= I1/(1+R1) + I2/[(1+R1)*(1+R2)] + (IN + N)/[(1+R1)*(1+R2)*..(1+Rn)],
где
I1, I2, In— процентный доход i-того периода (i = 1, 2, ..., п) R1, R2, Rn требуемая норма прибыли (ставка дисконтирования) i-того периода. При расчете цены облигации в данном случае необходимо оценить величину процентных выплат и требуемую норму прибыли для всех периодов.
Рассмотрим далее задачу определения цены бескупонной облигации. Ее можно представить как купонную облигацию с нулевым размером купонных платежей. Поскольку процентные платежи при этом равны нулю, то рассмотренная ранее формула принимает следующий вид:
P = N/(1+R)n
Задача. Бескупонная облигация номиналом 10000 руб. погашается по номиналу через 3 года. Определить курсовую цену облигации, если ставка дисконтирования составляет 15% годовых.
P = 10000/(1+0,15)3 = 6575,16 руб.
Рассмотренная формула может быть использована и при определении курсовой стоимости краткосрочных ценных бумаг – со сроком действия менее 1 года.
Задача. Определить цену краткосрочной облигации номиналом 1000 руб., погашение через 180 дней. Требуемая норма прибыли по данному типу облигаций составляет 20% годовых.
Используя полученную выше формулу получим:
P = 1000/(1+0,2)180/365= 914,01 руб.
Однако для определения цены краткосрочных облигаций обычно используется другая формула:
P = N/(1+R*T/365)
Применяя эту формулу, получаем:
P = 1000/(1+0,2*180/365)=910,22 руб.
Чтобы установить величину различий результатов вычислений при использовании представленных двух формул, рассмотрим ряд примеров.
Задача.
Номинал облигации — 1000 руб. Требуемая норма прибыли — 10% годовых, погашение — через 180 дней.
Цена облигации, вычисленная по первой формуле:
P = 1000/(1+0,1)180/365= 954,08 руб.
по второй формуле:
P= 1000/(1+0,1*180/365) = 953,00 руб.
Задача.
Номинал облигации — 1000 руб. Требуемая норма прибыли — 20% годовых, погашение — через 300 дней.
Цена облигации, вычисленная по первой формуле:
P = 1000/(1+0,2)300/365= 860,84 руб.
по второй формуле:
P= 1000/(1+0,2*300/365) = 858,83 руб.
Задача.
Номинал облигации — 1000 руб. Требуемая норма прибыли — 15% годовых, погашение — через 365 дней.
Цена облигации, вычисленная по первой формуле:
P = 1000/(1+0,15)= 869,56 руб.
по второй формуле:
P= 1000/(1+0,15*365/365) = 869,56 руб.
Доходность облигаций
Облигации приобретаются инвесторами с целью получение дохода. Для анализа эффективности вложений в разные виды облигаций, а также в другие ценные бумаги следует сопоставить величину получаемого дохода с величиной инвестиций с затратами на приобретение ценной бумаги. Различают следующие показатели доходности: купонная доходность, текущая доходность, доходность к погашению, доходность за период владения.
Купонная доходность (RК) устанавливается при выпуске облигации и для ее расчета используется следующая формула:
RК=I/N,
Где
I — купонный доход, N— номинальная цена облигации.
Текущая доходность (RT) определяется как отношение величины процентного дохода к цене приобретения облигации:
RT= I /P,
где
I — процентный доход,
Р — цена приобретения облигации.
Задача. Облигация номиналом 1000 руб. продается по цене 900 руб. процентный доход в размере 15% годовых выплачивается один раз в год. Определить купонную и текущую доходность облигации.
Купонная доходность будет равна:
RК=I/N = 150/1000 = 0,15 или 15% годовых
Текущая доходность будет равна:
RT= I /P = 150/900 = 0,167 или 16,7% годовых.
Доходность к погашению равна требуемой норме прибыли инвестора R, при которой приведенная стоимость денежных платежей по облигации равна ее рыночной стоимости. В течение срока жизни облигации происходит изменение ее рыночной цены и доходности вследствие изменения процентных ставок. Если инвестор собирается держать облигацию до погашения, то он может сопоставить все полученные по облигации доходы (процентные платежи и сумму погашения) с ценой приобретения облигации. Полученная таким способом величина называется доходностью к погашению или внутренней нормой прибыли.
Доходность к погашению можно определить методом последовательных приближений, используя полученную ранее формулу
P = I/R*[1-1/(1+R)n] + N/(1+R)n,
где
P – рыночная цена облигации,
R – доходность к погашению,
n – число периодов владения облигацией.
Метод последовательных приближений реализуется путем подстановки в данную формулу различные значения R и определения для каждого значения R соответствующего значения цены. Если для выбранного значения R мы получаем цену выше заданного значения цены (Р), то следует увеличить значение R и найти новое значение Р. Если получено значение Р ниже заданной цены, то необходимо уменьшить значение R. Такие действия необходимо продолжать до тех пор, пока расчетная цена не совпадет с заданной точностью с рыночной ценой. Полученное таким образом значение R и будет являться доходностью облигации к погашению или внутренней нормой прибыли облигации.
Задача. Номинал облигации — 1000 руб. Срок погашения облигации — через 3 года. По облигации выплачивается 15% годовых, выплата производится один раз в год. Курсовая цена облигации — 920 руб. Определить доходность облигации к погашению. В качестве первого приближения возьмем ставку дисконтирования равной 17%. Найдем цену облигации:
P = 150/0,17*[1-1/(1+0,17)3] + 1000/(1+0,17)3 = 955,81 руб.
Мы получим цену, которая выше курсовой цены облигации. Следовательно, ставка дисконтирования должна быть увеличена. Увеличим ее до 19% и найдем новое значение цены облигации:
P = 150/0,19*[1-1/(1+0,19)3] + 1000/(1+0,19)3 == 914,4 руб.
Мы получили значение цены, которое ниже курсовой цены облигации. Следовательно, чтобы получить значение цены, равное курсовой стоимости облигации ставка дисконтирования должна быть ниже 19%. Искомое значение находится между 17% и 19%. Продолжая представленные расчеты, можно найти значение доходности к погашению – 18,7%. Цена облигации в этом случае будет равна
P = 150/0,187*[1-1/(1+0,187)3] + 1000/(1+0,187)3 = 920,45 руб.
Таким образом, при ставке дисконтирования равной 18,7% текущая стоимость процентных платежей и суммы погашения облигации равна покупной цене облигации – затратам инвестора. Это означает, что доходность облигации к погашению составляет 18,7%. Использование показателя доходности к погашению позволяет инвестору решить вопрос о приемлемости инвестиций в приобретение облигации.
В реальных ситуациях для принятия того или иного решения не всегда необходимо производить точные вычисления, так как многие факторы, определяющие доходность финансовых инструментов, остаются вне контроля инвестора. В этом случае для получения приблизительного результата можно использовать следующую формулу:
R = [(N-P)/n+I]/[(N+P)/2],
где
N — номинал облигации;
Р— цена облигации;
п — число лет до погашения облигации;
I — ежегодный процентный доход.
Для приведенного выше Примера имеем:
R = [(1000-920)/3+150]/[(1000+920)/2] = 18,4%.
Отклонение значения доходности, полученного с помощью приближенной формулы, весьма незначительно и находится в пределах допустимой ошибки.
Бескупонная облигация
Для определения доходности бескупонной облигации (облигации с нулевым купоном) необходимо воспользоваться формулой для определения цены облигации:
P = N/(1+R)n.
После преобразований получаем следующее выражение для доходности бескупонной облигации:
R= 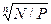- 1
Задача. Определить доходность бескупонной облигации номинальной стоимостью 1000 руб. Рыночная цена облигации равна 700 руб. и до погашения остается 3 года. Доходность определяется из представленного выше выражения
R= 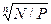- 1 = 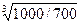- 1 = 0,126 или же 12,6%.
Доходность краткосрочных облигаций (сроком действия до 1 года) обычно определяется по формуле:
R = (DI/P) * (365/T)
где DI — величина дисконта; Р –цена облигации; Т — число дней до погашения облигации. Подставляя вместо D = N-Р, получаем:
R = [(N-P)/P] * (365/T) = (N/P-1)*(365/T)
Задача. Облигация номиналом 1000 руб. продается с дисконтом по цене 950 рублей. До погашения облигации остается 60 дней. Определить доходность к погашению. Используя полученное выше выражение получаем:
R = (1000/950-1)*(365/60) = 0,320 или же 32,0%
Дата: 2019-02-25, просмотров: 199.
