Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

q - заряд (Кл), t - время (с)

3

ε_i = -  N ∆Ф / ∆t

Закон электромагнитной индукции

∆Ф – изменение магнитного потока (Вб), ∆ t- промежуток времени (с), N – число витков соленоида

4

ε_i  = B L υ sin α

ЭДС индукции в движущемся проводнике

В – модуль вектора магнитной индукции (Тл), L  - длина проводника (м), υ - скорость движения проводника в магнитном поле (м/с),  α - угол между векторами скорости и магнитной индукции.

5

 Ф = BS cos α

Магнитный поток

B - модуль вектора магнитной индукции (Тл), S -  площадь витка контура ( м²),  α -  угол между вектором магнитной индукции и нормалью к поверхности

6

ε_si  = - L∆I / ∆t

ЭДС самоиндукции

L - индуктивность катушки (Гн), ∆I /∆t- скорость изменения тока в катушке

( А/с)

7

L = / I

Индуктивность катушки (коэффициент пропорциональности, зависящий от формы, размеров проводника и магнитных свойств среды)

Ф – магнитный поток (Вб), I - сила тока в проводнике (А)

8

W = L I² / 2

Энергия магнитного поля тока (Дж)

L – индуктивность (Гн),  I – сила тока в катушке (А)

Механические колебания и волны

1

Т = 1/ν = n / t

Период колебаний

T – период колебаний (с),  ν – частота колебаний (Гц),  n – число колебаний ,  t – время n  колебаний (с)

2

Т = 2π /ω , где  ω = 2πν

Период гармонических колебаний

ω – циклическая или круговая частота (рад/с)

3

υ = х´ = - Х_махω sin(ωt +φ)

Скорость колеблющейся точки

Х_мах – амплитуда колебаний ( м), φ – начальная  фаза колебаний

4

а = υ´ = х´´ = - Х_махω² со (ωt +φ)

Ускорение колеблющейся точки

 υ _мах = Х_махω , где υ _мах  - амплитудное значение скорости,

 а_мах= Х_махω ², где а_{мах –} амплитудное значение ускорения

5

а =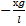

Ускорение математического маятника для малых углов

Х – смещение (м), l -  длина нити (м),  g – ускорение свободного падения (м/с²)

6

T = 2π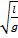

Период собственных колебаний математического маятника

T –период (с),  l -  длина нити (м),  g – ускорение свободного падения (м/с²)

7

ν = 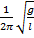; ω =

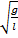
Частота и циклическая частота собственных колебаний математического маятника

ω – циклическая частота (рад/с),   ν – частота (Гц)

8

a = -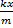

Ускорение пружинного маятника

k - жесткость пружины (Н/м), m  - масса груза (кг), х – смещение (м)

9

T = 2π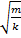

Период колебаний пружинного маятника

T –период (с),  k - жесткость пружины (Н/м), m  - масса груза (кг)

10

ν = 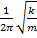: ω =

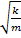
Частота и циклическая частота собственных колебаний  пружинного маятника

ν - частота (Гц), k - жесткость пружины (Н/м), m  - масса груза (кг), ω – циклическая частота (рад/с)

11

E_n = E_k + E_p = m Х_мах ² ω² / 2

Полная энергия при гармонических колебаниях

Е_к – кинетитческая энергия (Дж), Е_р – потенциальная энергия (Дж), Х_мах – амплитуда колебаний ( м),  ω – циклическая или круговая частота (рад/с)

12

Х_мах = F _max / μ ω₀

Амплитуда вынужденных колебаний при резонансе

Х_мах – амплитуда колебаний ( м), - амплитудное значение внешней силы (Н), μ – коэффициент трения, ω₀ – частота собственных колебаний (рад/с)

13

λ = υ T = υ / ν