Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

L1: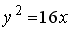

L2: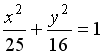

L3: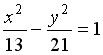

R1: Парабола

R2: Эллипс

R3: Гипербола

R4: окружность

I:

Q: Укажите соответствие между уравнениями и видами кривых второго порядка.

L1: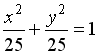

L2: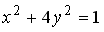

L3: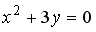

R1: окружность

R2: эллипс

R3: парабола

R4: гипербола

I:

Q: Укажите соответствие между уравнениями и видами кривых второго порядка.

L1: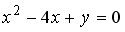

L2: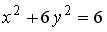

L3: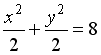

R1: парабола

R2: эллипс

R3: окружность

R4: гипербола

I:

Q: Укажите соответствие между уравнениями и видами кривых второго порядка.

L1: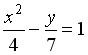

L2: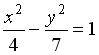

L3: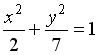

R1: парабола

R2: гипербола

R3: эллипс

R4: окружность

I:

Q: Укажите соответствие между уравнениями и видами кривых второго порядка.

L1: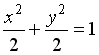

L2: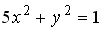

L3: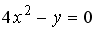

R1: окружность

R2: эллипс

R3: парабола

R4: гипербола

I:

Q: Укажите соответствие между уравнениями и видами кривых второго порядка.

L1: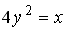

L2: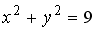

L3: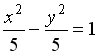

R1: парабола

R2: окружность

R3: гипербола

R4: эллипс

I:

Q: Укажите соответствие между уравнениями и видами кривых второго порядка.

L1: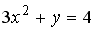

L2: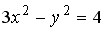

L3: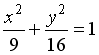

R1: парабола

R2: гипербола

R3: эллипс

R4: окружность

I:

Q: Укажите соответствие между уравнениями и видами кривых второго порядка.

L1: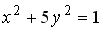

L2: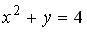

L3: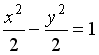

R1: эллипс

R2: парабола

R3: гипербола

R4: окружность

I:

Q: Укажите соответствие между уравнениями и видами кривых второго порядка.

L1: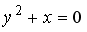

L2: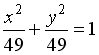

L3: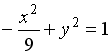

R1: парабола

R2: окружность

R3: гипербола

R4: эллипс

I:

Q: Укажите соответствие между уравнениями и видами кривых второго порядка.

L1: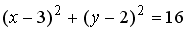

L2: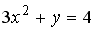

L3: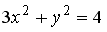

R1: окружность

R2: парабола

R3: эллипс

R4: гипербола

V3: Аналитическая геометрия в пространстве

I:

S: Нормальный вектор плоскости 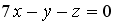имеет координаты…

-: (7; 0; – 1)

+: (7; – 1; – 1)

-: (– 7; 1; 1)

-: (7; 0; 0)

I:

S: Вектор 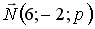перпендикулярен плоскости 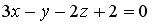. Тогда значение p равно …

-: 10

-: – 6

+: – 4

-: 6

I:

S: Плоскост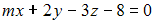и и 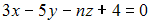параллельны при значениях 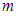и 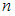, равных …

-: ;

-: ;

+: ;

-: ;

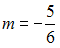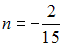
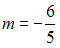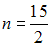
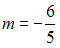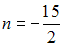
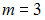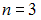
I:

S: Координата 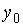точки 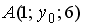, принадлежащей плоскости 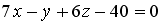, равна…

-: 5

+: 3

-: 4

-: 2

I:

S: Координата 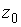точки 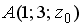, принадлежащей плоскости 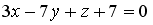, равна…

-: 7

-: 10

-: 13

+: 11

I:

S: Координата 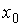точки 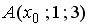, принадлежащей плоскости 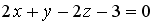, равна…

-: 5

-: 3

-: 6

+: 4

I:

S: Координата 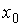точки 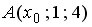, принадлежащей плоскости 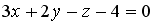, равна…

+: 2

-: 3

-: 4

-: 1

I:

S: Координата 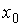точки 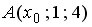, принадлежащей плоскости 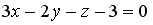, равна…

-: 4

-: 1

-: 2

+: 3

I:

S: Уравнение прямой, проходящей через точку 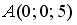перпендикулярно плоскости 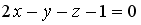, имеет вид…

-:

-:

-:

+:

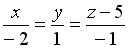
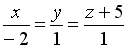
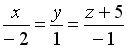
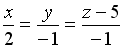
I:

S: Уравнение прямой, проходящей через точку 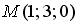перпендикулярно плоскости 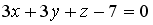, имеет вид…

+:

-:

-:

-:

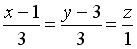
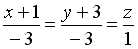
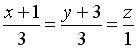
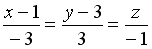
I:

S: Уравнение прямой, проходящей через точку 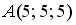перпендикулярно плоскости 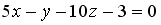, имеет вид…

-:

-:

-:

+:

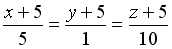
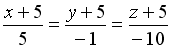
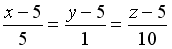
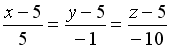
I:

S: Уравнение прямой, проходящей через точку 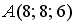перпендикулярно плоскости 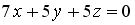, имеет вид…

-:

-:

-:

+:

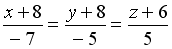
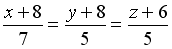
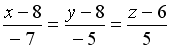
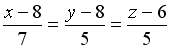
I:

S: Точкой пересечения плоскости 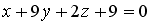с осью 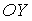является …

-:

-:

-:

+:

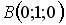
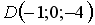
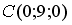
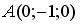
V2: Комплексные числа

V3: Комплексные числа и их представление.

I:

S: Модуль комплексного числа 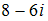равен …

-: 2

-: 14

+: 10

-:

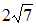
I:

Q: Установите соответствие между комплексным числом и его модулем

L1: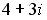

L2: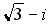

L3: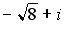

L4: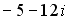

R1: 5

R2: 2

R3: 3

R4: 13

R5:  7

I:

S: Аргумент комплексного числа 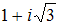равен …

-:

+:

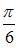
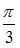
-: 2

-:

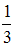
I:

Q: Установите соответствие между комплексным числом и его аргументом

L1: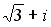

L2: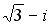

L3: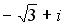

R1: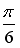

R2: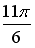

R3: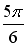

R4: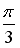

I:

Q: Установите соответствие между комплексным числом и его аргументом

L1: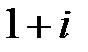

L2: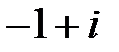

L3: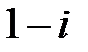

R1: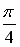

R2: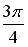

R3: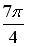

R4: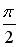

I: