КАЗАНСКИЙ КООПЕРАТИВНЫЙ ИНСТИТУТ (ФИЛИАЛ)
УТВЕРЖДАЮ
 Проректор по учебной работе
Проректор по учебной работе
А.Р. Набиева
«09» сентября 2016 года
Математика
ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ДЛЯ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ
Фонд оценочных средств для промежуточной аттестации по дисциплине обсужден и рекомендован на заседании кафедры естественных дисциплин, сервиса и туризма «02» сентября 2016 года, протокол №1.
Заведующий кафедрой Ф.Ф. Ибляминов
ПАСПОРТ
| № | Наименование пункта | Значение |
| 1. | Кафедра | Естественные дисциплины, сервис и туризм |
| 2. | Автор – разработчик | Поташев А.В., д.ф.-м.н., профессор Поташева Е.В., к.т.н., доцент |
| 3. | Наименование дисциплины | Математика |
| 4. | Общая трудоемкость по учебному плану | 144 |
| 5. | Вид контроля (нужное подчеркнуть) | Предварительный (входной), текущий, промежуточный (экзамен) |
| 6. | Для специальности(ей)/ направления(й) подготовки | 38.05.02 Таможенное дело , нормативный срок , очная и заочная формы обучения |
| 7. | Количество тестовых заданий всего по дисциплине, из них | 442 |
| 8. | Количество заданий при тестировании студента | 24 |
| 9. | Из них правильных ответов (в %): | |
| 10. | для оценки «отлично» | 86 % и больше |
| 11. | для оценки «хорошо» | 71 % - 85% |
| 12. | для оценки «удовлетворительно» | 50% - 70% |
| 13. | или для получения оценки «зачет» не менее | - |
| Время тестирования (в минутах) | 45 |
СОДЕРЖАНИЕ
Стр.
V1: Алгебра и геометрия.. 5
V2: Линейная алгебра. 5
V3: Определители. 5
V3: Линейные операции над матрицами. 10
V3: Произведение матриц. 14
V3: Обратная матрица. 20
V3: Системы линейных уравнений. 22
V3: Векторная алгебра. 31
V2: Аналитическая геометрия. 34
V3: Прямая на плоскости. 34
V3: Кривые второго порядка. 36
V3: Аналитическая геометрия в пространстве. 41
V2: Комплексные числа. 44
V3: Комплексные числа и их представление. 44
V3: Операции над комплексными числами. 47
V1: Математический анализ. 49
V2: Элементы теории пределов. 49
V3: Понятие функции. 49
V3: Предел функции на бесконечности. 53
V3: Предел функции в точке. 56
V3: Непрерывность функции, точки разрыва. Асимптоты графика функции 65
V2: Дифференциальное исчисление функций одной переменной. 70
V3: Производные первого порядка. 70
V3: Производные сложной функции. 79
V3: Производные высших порядков. 81
V3: Приложения дифференциального исчисления ФОП. 82
V2: Дифференциальное исчисление функций нескольких переменных. 86
V3: Частные производные первого порядка. 86
V3: Частные производные высших порядков. 88
V2: Интегральное исчисление. 90
V3: Неопределенный интеграл. 90
V3: Определенный интеграл. 92
V3: Несобственные интегралы.. 95
F1: Математика экзамен 2016/2017
F2: Поташев А.В., Поташева Е.В.
F3: Тестовые задания по направлению подготовки 38.05.02 Таможенное дело очная и заочная формы нормативный срок 442 задания, 24 вопроса, 144 часа
F4: Дидактическая единица; Раздел; Тема
V1: Алгебра и геометрия
V2: Линейная алгебра
V3: Определители
I:
S: Формула вычисления определителя третьего порядка  содержит следующие произведения: …
содержит следующие произведения: …
+: 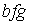
-: 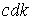
-: 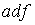
+: 
I:
S: Формула вычисления определителя третьего порядка 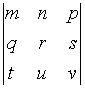 содержит следующие произведения: …
содержит следующие произведения: …
+: 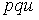
-: 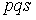
+: 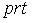
-: 
I:
S: Формула вычисления определителя третьего порядка  содержит следующие произведения: …
содержит следующие произведения: …
+: 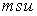
+: 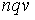
-: 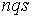
-: 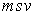
I:
S: Формула вычисления определителя третьего порядка  содержит следующие произведения: …
содержит следующие произведения: …
+: 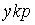
+: 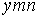
-: 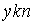
-: 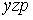
I:
S: Формула вычисления определителя третьего порядка  содержит следующие произведения: …
содержит следующие произведения: …
+: 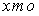
-: 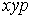
-: 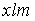
+: 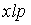
I:
S: Формула вычисления определителя третьего порядка  содержит следующие произведения: …
содержит следующие произведения: …
-: 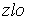
-: 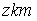
+: 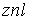
+: 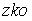
I:
S: Формула вычисления определителя третьего порядка  содержит следующие произведения: …
содержит следующие произведения: …
-: 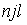
+: 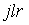
+: 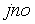
-: 
I:
S: Формула вычисления определителя третьего порядка  содержит следующие произведения: …
содержит следующие произведения: …
+: 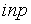
+: 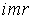
-: 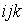
-: 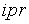
I:
S: Определитель 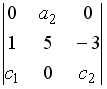 равен…
равен…
-: 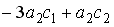
-: 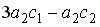
-: 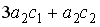
+: 
I:
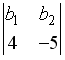
S: Разложение определителя 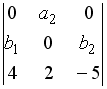 по элементам первой строки имеет вид…
по элементам первой строки имеет вид…
+: 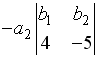
-: 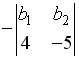
-: 
-: 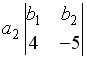
I:
S: Определитель 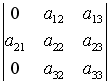 равен…
равен…
+: 
-: 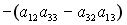
-: 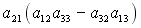
-: 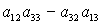
I:
S: Разложение определителя 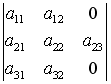 по элементам третьего столбца имеет вид …
по элементам третьего столбца имеет вид …
-: 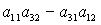
+: 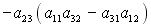
-: 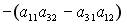
-: 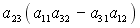
I:
S: Определитель 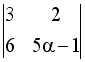 равен 0, если
равен 0, если 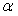 равно …
равно …
-: 2
-: – 4
-: 0
+: 1
I:
S: Определитель 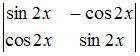 равен …
равен …
-: 0
-: 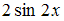
+: 1
-: 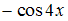
I:
S: Определитель 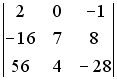 равен ###
равен ###
+: 0
I:
S: Определитель 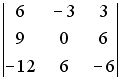 равен ###
равен ###
+: 0
I:
S: Определитель 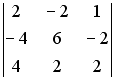 равен ###
равен ###
+: 0
I:
S: Определитель 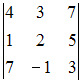 равен ###
равен ###
+: 35
I:
S: Определитель 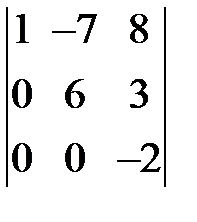 равен ###
равен ###
+: -12
I:
S: Определитель 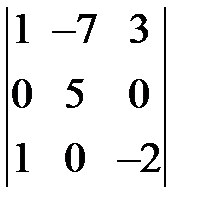 равен ###
равен ###
+: -25
I:
S: Определитель  равен ###
равен ###
+: 2
I:
S: Определитель 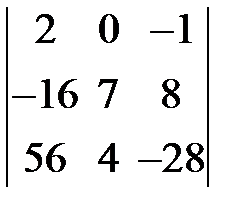 равен ###
равен ###
+: 0
I:
S: Определитель 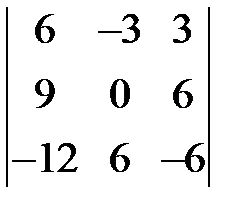 равен ###
равен ###
+: 0
I:
S: Определитель  равен ###
равен ###
+: 0
V3: Произведение матриц
I:
S: Для матриц А и В найдено произведение 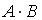 , причем
, причем 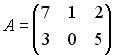 . Тогда матрицей В может быть матрица …
. Тогда матрицей В может быть матрица …
-: 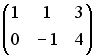
-: 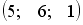
+: 
-: 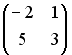
I:
S: Операция произведения матриц правильно определена для матричного произведения вида …
+: 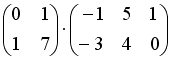
-: 
+: 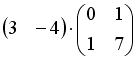
+: 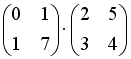
-: 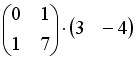
I:
S: Операция произведения матриц правильно определена для матричного произведения вида …
-: 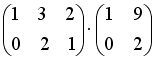
+: 
-: 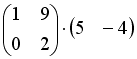
+: 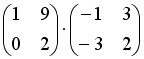
+: 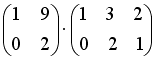
I:
S: Операция произведения матриц правильно определена для матричного произведения вида …
+: 
-: 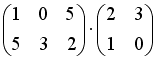
+: 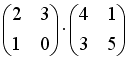
-: 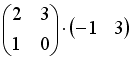
+: 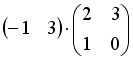
I:
S: Операция произведения матриц правильно определена для матричного произведения вида …
+: 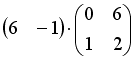
+: 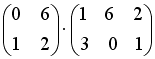
-: 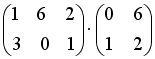
-: 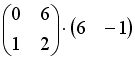
+: 
I:
S: Операция произведения матриц правильно определена для матричного произведения вида …
+: 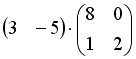
+: 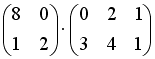
-: 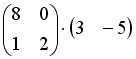
+: 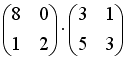
-: 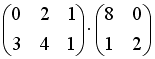
I:
S: Заданы матрицы 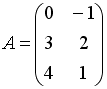 ,
, 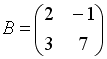 . Тогда элемент
. Тогда элемент 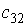 матрицы
матрицы 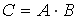 равен …
равен …
+: 3
-: −11
-: −7
-: 5
I:
S: Дана матрица 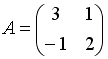 . Тогда элемент
. Тогда элемент 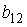 матрицы
матрицы 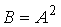 равен …
равен …
+: 5
-: – 5
-: – 1
-: 1
I:
S: Элемент 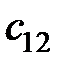 в произведении матриц
в произведении матриц 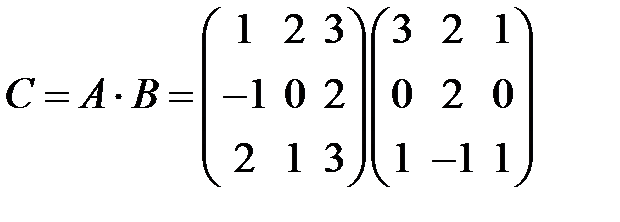 равен ###
равен ###
+: 3
I:
S: Элемент 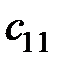 в произведении матриц
в произведении матриц 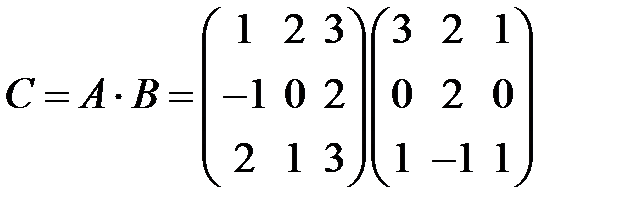 равен ###
равен ###
+: 6
I:
S: Элемент 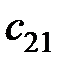 в произведении матриц
в произведении матриц 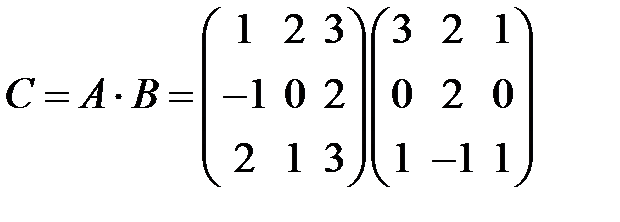 равен ###
равен ###
+: -1
I:
S: Элемент 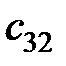 в произведении матриц
в произведении матриц 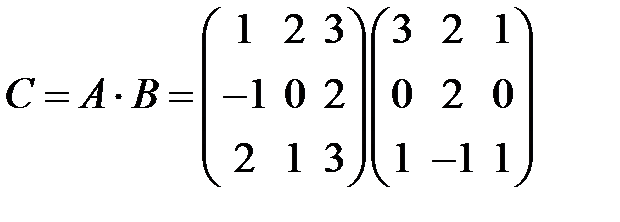 равен ###
равен ###
+: 3
I:
S: Заданы матрицы 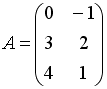 ,
, 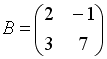 . Тогда элемент
. Тогда элемент 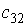 матрицы
матрицы 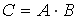 равен …
равен …
+: 3
-: − 11
-: − 7
-: 5
I:
S: Дана матрица 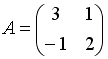 . Тогда элемент
. Тогда элемент 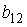 матрицы
матрицы 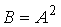 равен …
равен …
+: 5
-: – 5
-: – 1
-: 1
I:
S:Если 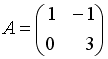 ,
, 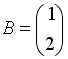 , тогда матрица
, тогда матрица 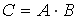 имеет вид …
имеет вид …
-: 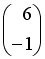
+: 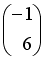
-: 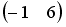
-: 
I:
S: Если 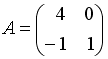 ,
,  , тогда матрица
, тогда матрица 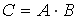 имеет вид …
имеет вид …
+: 
-: 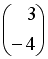
-: 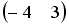
-: 
I:
S:Если 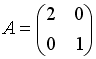 ,
, 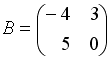 , тогда матрица
, тогда матрица 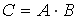 имеет вид …
имеет вид …
-: 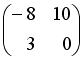
-: 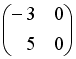
-: 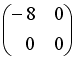
+: 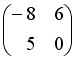
I:
S:Если  ,
, 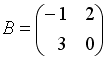 , тогда матрица
, тогда матрица 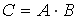 имеет вид …
имеет вид …
+: 
-: 
-: 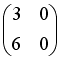
-: 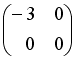
I:
S: Дана матрица 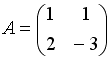 . Тогда матрица
. Тогда матрица 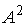 имеет вид …
имеет вид …
-: 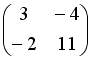
-: 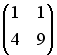
-: 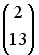
+: 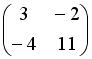
I:
S: Дана матрица 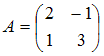 . Тогда матрица
. Тогда матрица 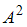 имеет вид …
имеет вид …
-: 
-: 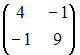
+: 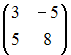
-: 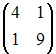
I:
S: Дана матрица 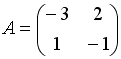 . Тогда матрица
. Тогда матрица 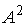 имеет вид …
имеет вид …
-: 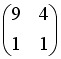
-: 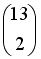
+: 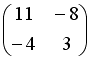
-: 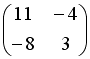
V3: Обратная матрица
I:
S: Матрица 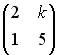 не имеет обратной при k, равном …
не имеет обратной при k, равном …
-: 0
+: 10
-: -10
-: 5
I:
S: Матрица 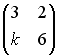 не имеет обратной при k, равном …
не имеет обратной при k, равном …
-: 3
-: 10
+: 9
-: -9
I:
S: Матрица 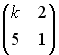 не имеет обратной при k, равном …
не имеет обратной при k, равном …
+: 10
-: 3
-: -10
-: 0
I:
S: Для каких из матриц 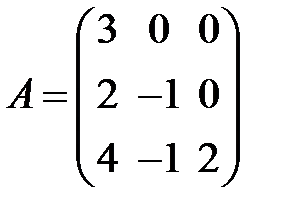 ,
,  ,
, 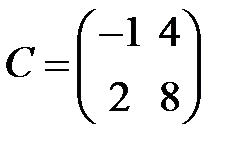 ,
, 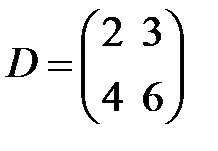 существует обратная.
существует обратная.
+: A
-: B
+: C
-: D
I:
S: Для каких из матриц 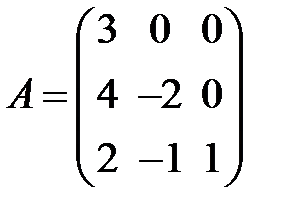 ,
, 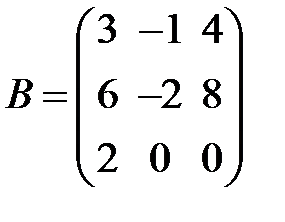 ,
, 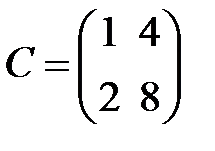 ,
, 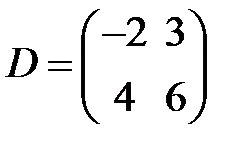 существует обратная
существует обратная
+: A
-: B
-: C
+: D
I:
S: Для каких из матриц 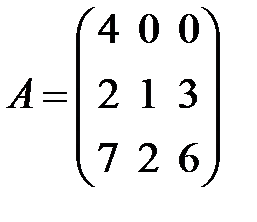 ,
,  ,
, 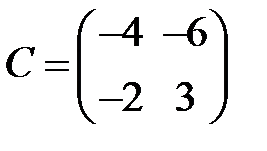 ,
, 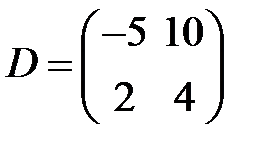 не существует обратная
не существует обратная
+: A
+: B
-: C
-: D
I:
S: Матрица 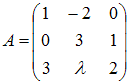 не имеет обратной, при
не имеет обратной, при 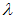 , равном …
, равном …
-: 3
-: 12
+: 0
-: – 12
I:
S: Дана матрица 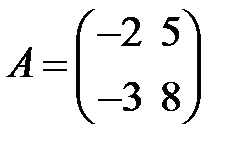 . Тогда обратная матрица
. Тогда обратная матрица 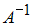 равна …
равна …
+: 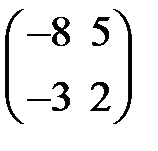
-: 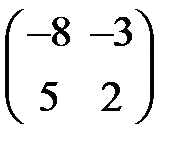
-: 
-: 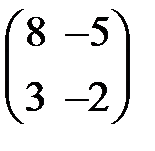
I:
S: Дана матрица 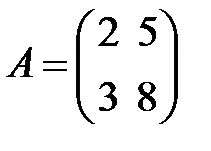 . Тогда обратная матрица
. Тогда обратная матрица 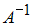 равна …
равна …
+: 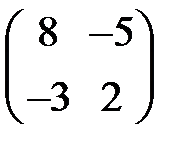
-: 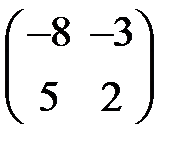
-: 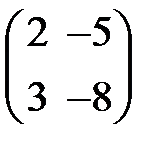
-: 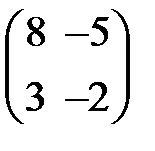
V3: Векторная алгебра
I:
S: Известны координаты точек 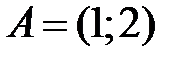 и
и 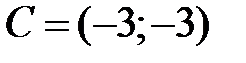 . Если
. Если 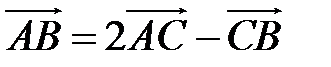 , то координаты точки
, то координаты точки 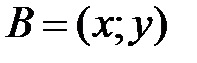 равны …
равны …
-: 
+: 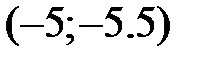
-: 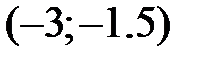
-: 
I:
S: Даны векторы 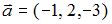 и
и 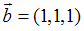 ; если
; если 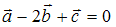 , то вектор
, то вектор 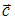 равен …
равен …
-: 
-: 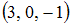
+: 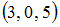
-: 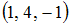
I:
S: Даны векторы 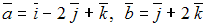 . Тогда линейная комбинация
. Тогда линейная комбинация 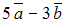 этих векторов равна …
этих векторов равна …
-: 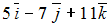
-: 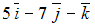
+: 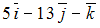
-: 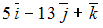
I:
S: Направляющим для прямой, заданной уравнением 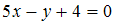 , будет вектор …
, будет вектор …
-: 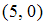
-: 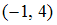
+: 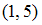
-: 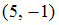
I:
S: Площадь треугольника, образованного векторами 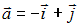 и
и 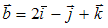 , равна …
, равна …
-: 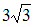
-: 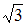
+: 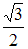
-: 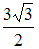
I:
S: Длина стороны квадрата, площадь которого равна площади параллелограмма, построенного на векторах  и
и 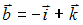 , равна …
, равна …
-: 1
-: 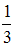
+: 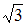
-: 3
I:
S: Векторное произведение векторов 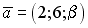 и
и 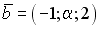 равно нулю, если…
равно нулю, если…
-: 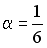 ;
; 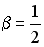
+: 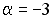 ;
; 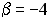
-: 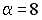 ;
; 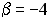
-: 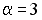 ;
; 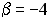
I:
S: Векторное произведение векторов 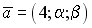 и
и 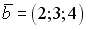 равно нулю, если…
равно нулю, если…
-: 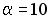 ;
; 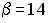
-: 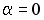 ;
; 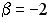
-: 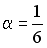 ;
; 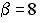
+:  ;
; 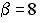
I:
S: Векторное произведение векторов 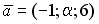 и
и 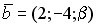 равно нулю, если…
равно нулю, если…
-: 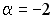 ;
; 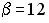
-: 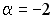 ;
; 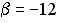
+: 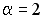 ;
; 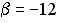
-: 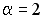 ;
; 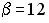
I:
S: Векторное произведение векторов 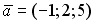 и
и 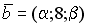 равно нулю, если…
равно нулю, если…
-: 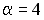 ;
; 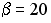
+:  ;
; 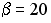
-:  ;
; 
-: 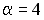 ;
; 
I:
S: Векторное произведение векторов 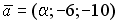 и
и 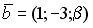 равно нулю, если…
равно нулю, если…
-: 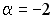 ;
; 
+: 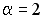 ;
; 
-: 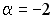 ;
; 
-: 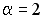 ;
; 
V2: Аналитическая геометрия
V3: Прямая на плоскости
I:
S: Положительный угловой коэффициент имеют прямые:

-: h
+: u
+: f
-: g
I:
S: Отрицательный угловой коэффициент имеют прямые:
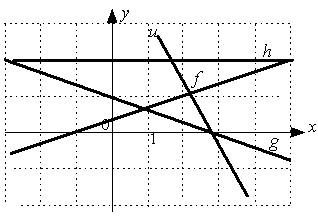
-: h
+: u
-: f
+: g
I:
S: Положительный угловой коэффициент имеют прямые:
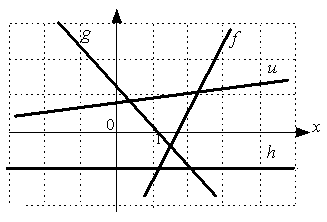
-: h
-: g
+: u
+: f
I:
S: Расстояние от точки 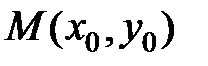 до прямой
до прямой 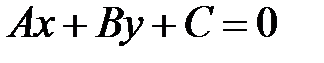 можно найти по формуле
можно найти по формуле
+: 
-: 
-: 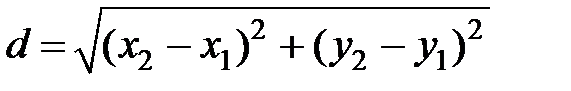
I:
S: Расстояние от точки 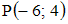 до прямой
до прямой 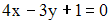 равно …
равно …
-: 
+: 7
-: 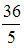
-: 35
I:
S: Острый угол между прямыми линиями 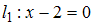 и
и  равен …
равен …
-: 
+: 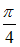
-: 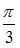
-: 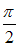
I:
S: Прямые 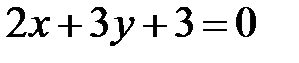 и
и 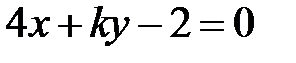 параллельны при
параллельны при 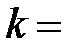 ###
###
+: 6
I:
S: Прямые 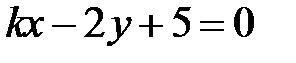 и
и 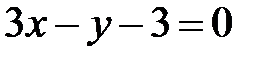 параллельны при
параллельны при 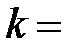 ###
###
+: 6
I:
S: Прямые 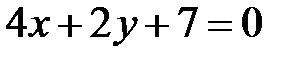 и
и  параллельны при
параллельны при 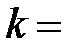 ###
###
+: -2
I:
S: Прямые 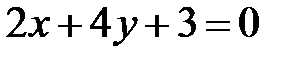 и
и  перпендикулярны при
перпендикулярны при 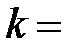 ###
###
+: -1/2
I:
S: Прямые 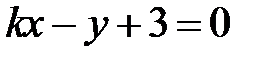 и
и  перпендикулярны при
перпендикулярны при 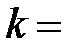 ###
###
+: -2
V3: Кривые второго порядка.
I:
S: Расстояние между фокусами эллипса 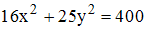 равно ###
равно ###
+: 6
I:
S: Расстояние между фокусами эллипса 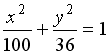 равно ###
равно ###
+: 16
I:
S: Расстояние между фокусами гиперболы 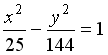 равно ###
равно ###
+: 26
I:
S: Расстояние между фокусами гиперболы 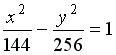 равно ###
равно ###
+: 40
I:
S: Расстояние между фокусами гиперболы 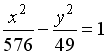 равно ###
равно ###
+: 50
I:
S: Вещественная полуось гиперболы, заданной уравнением 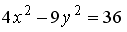 , равна ###
, равна ###
+: 3
I:
S: Мнимая полуось гиперболы, заданной уравнением 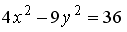 , равна ###
, равна ###
+: 2
I:
S: Мнимая полуось гиперболы, заданной уравнением 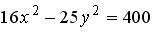 , равна ###
, равна ###
+: 4
I:
S: Мнимая полуось гиперболы, заданной уравнением 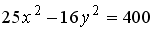 , равна ###
, равна ###
+:5
I:
S: Большая полуось эллипса, заданного уравнением 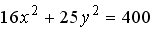 , равна ###
, равна ###
+: 5
I:
S: Если прямая 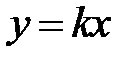 уравнение асимптоты гиперболы
уравнение асимптоты гиперболы 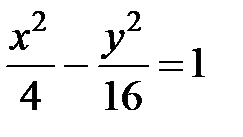 , то значение
, то значение 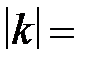 ###
###
+: 2
I:
S: Если прямая 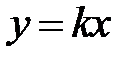 уравнение асимптоты гиперболы
уравнение асимптоты гиперболы 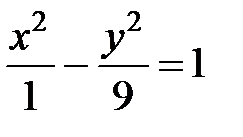 , то значение
, то значение  ###
###
+: 3
I:
S: Если прямая 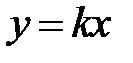 уравнение асимптоты гиперболы
уравнение асимптоты гиперболы 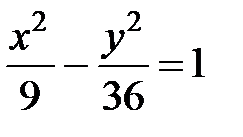 , то значение
, то значение  ###
###
+: 2
I:
S: Уравнение 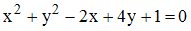 определяет окружность с центром в точке …
определяет окружность с центром в точке …
+: 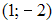
-: 
-: 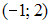
-: 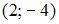
I:
V2: Комплексные числа
V1: Математический анализ
V3: Понятие функции
I:
S: Пусть 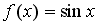 . Тогда сложная функция
. Тогда сложная функция 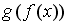 нечетна, если функция
нечетна, если функция 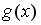 задается формулами…
задается формулами…
+: 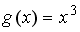
-: 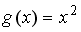
-: 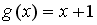
+: 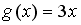
I:
S: Пусть 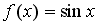 . Тогда сложная функция
. Тогда сложная функция 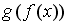 нечетна, если функция
нечетна, если функция 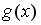 задается формулами…
задается формулами…
+: 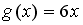
-: 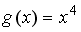
-: 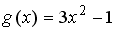
+: 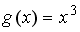
I:
S: Пусть 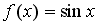 . Тогда сложная функция
. Тогда сложная функция 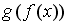 четна, если функция
четна, если функция 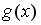 задается формулами…
задается формулами…
+: 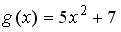
-: 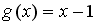
-: 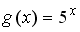
+: 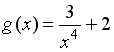
I:
S: Пусть 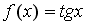 . Тогда сложная функция
. Тогда сложная функция 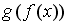 нечетна, если функция
нечетна, если функция 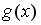 задается формулами…
задается формулами…
+: 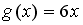
-: 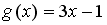
-: 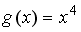
+: 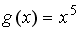
I:
S: Пусть 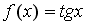 . Тогда сложная функция
. Тогда сложная функция 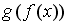 четна, если функция
четна, если функция 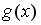 задается формулами…
задается формулами…
+: 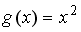
-: 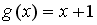
+: 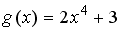
-: 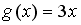
I:
S: Областью определения функции 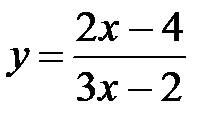 является множество точек вида
является множество точек вида
+: 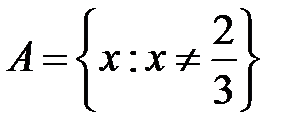
-: 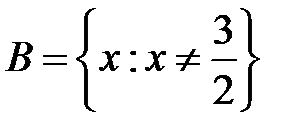
-: 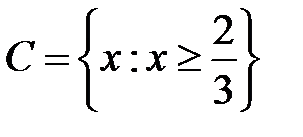
-: 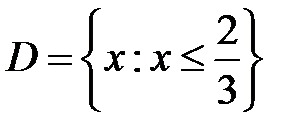
I:
S: Областью определения функции 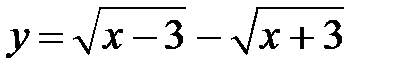 является множество точек вида
является множество точек вида
-: 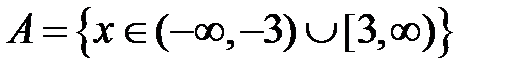
-: 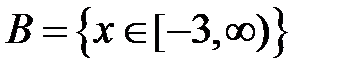
+: 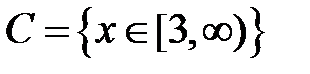
-: 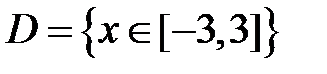
I:
S: Областью определения функции 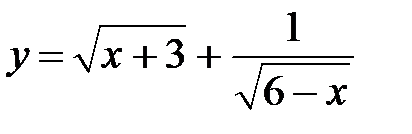 является множество точек вида
является множество точек вида
-: 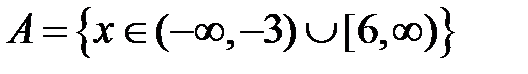
+: 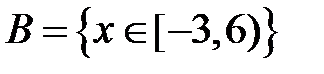
-: 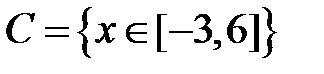
-: 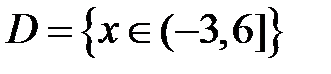
I:
S: Областью определения функции 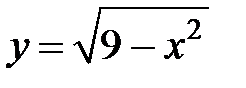 является множество точек вида
является множество точек вида
-: 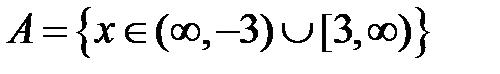
-: 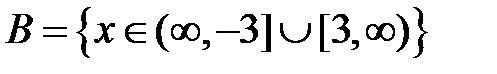
-: 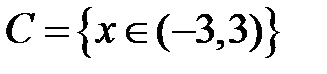
+ : 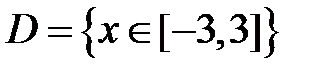
I:
S: Областью определения функции 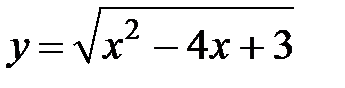 является множество точек вида
является множество точек вида
-: 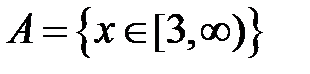
-: 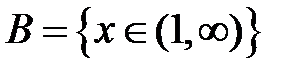
+ : 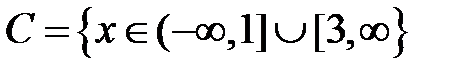
-: 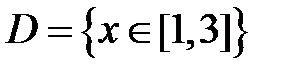
I:
S: Областью определения функции 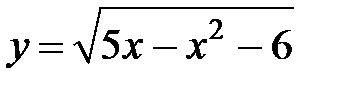 является множество точек вида
является множество точек вида
-: 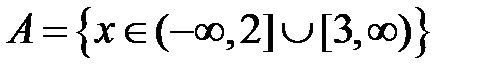
-: 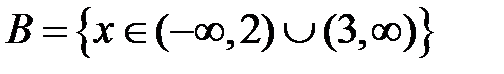
-: 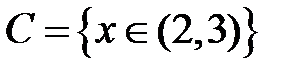
+: 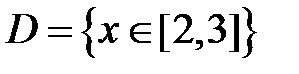
I:
S: Областью определения функции 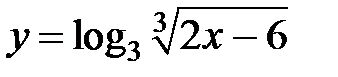 является множество точек вида
является множество точек вида
+: 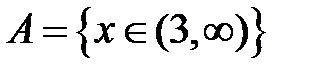
-: 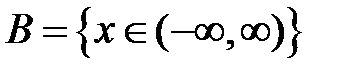
-: 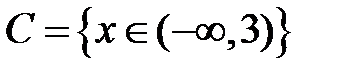
-: 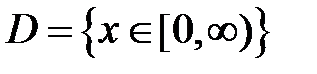
I:
S: Областью определения функции 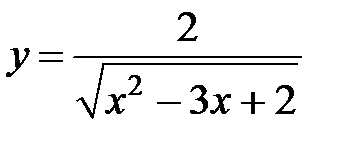 является множество точек вида
является множество точек вида
+: 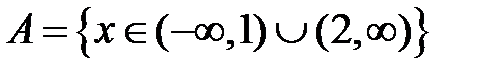
-: 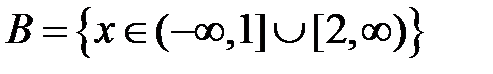
-: 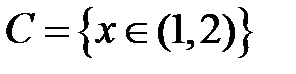
-: 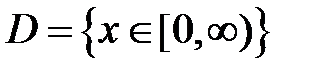
I:
S: Областью определения функции 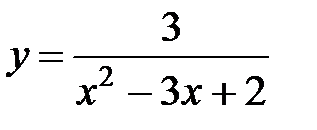 является множество точек вида
является множество точек вида
-: 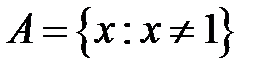
-: 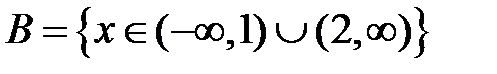
-: 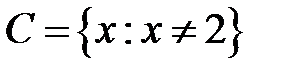
+: 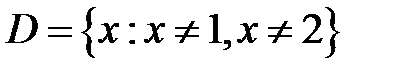
I:
S: Областью определения функции 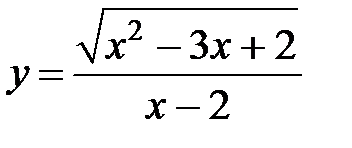 является множество точек вида
является множество точек вида
-: 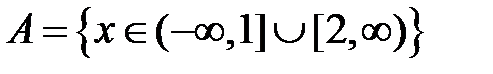
+: 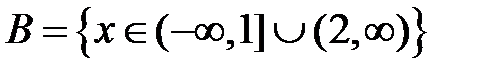
-: 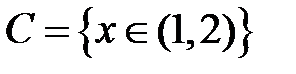
-: 
I:
S: Областью определения функции 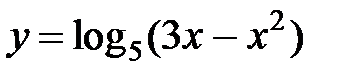 является множество точек вида
является множество точек вида
-: 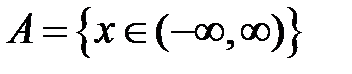
-: 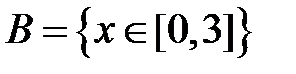
+: 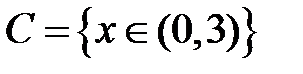
-: 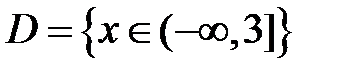
I:
S: Количество целых чисел, принадлежащих области определения функции 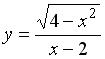 равно ###
равно ###
+: 4
I:
S: Количество целых чисел, принадлежащих области определения функции 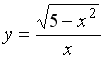 равно ###
равно ###
+: 4
I:
S: Количество целых чисел, принадлежащих области определения функции 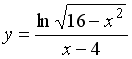 равно ###
равно ###
+: 7
I:
S: Количество целых чисел, принадлежащих области определения функции 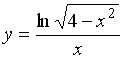 равно ###
равно ###
+: 2
I:
S: Количество целых чисел, принадлежащих области определения функции 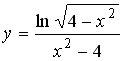 равно ###
равно ###
+: 3
V3: Предел функции в точке
I:
S: Предел функции 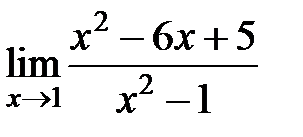 равен ###
равен ###
+: -2
I:
S: Предел функции 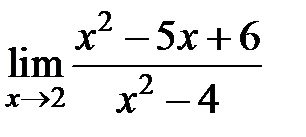 равен ###
равен ###
+: -1/4
I:
S: Предел функции 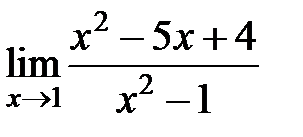 равен ###
равен ###
+: -3/2
I:
S: Предел функции 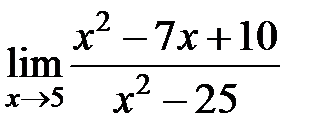 равен ###
равен ###
+: 3/10
I:
S: Предел функции 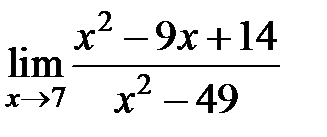 равен ###
равен ###
+: 5/14
I:
S: Предел функции 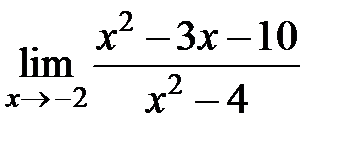 равен ###
равен ###
+: 7/4
I:
S: Предел функции 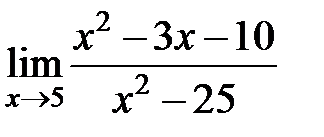 равен ###
равен ###
+: 7/10
I:
S: Предел функции 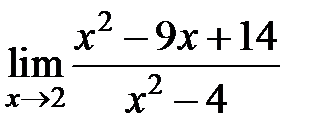 равен ###
равен ###
+: -5/4
I:
S: Предел функции 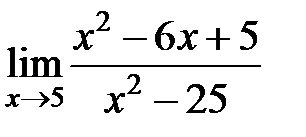 равен ###
равен ###
+: 2/5
I:
S: Предел функции 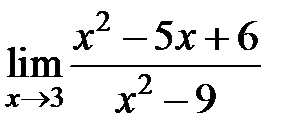 равен ###
равен ###
+: 1/6
I:
S: Предел функции 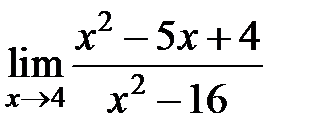 равен ###
равен ###
+: 3/8
I:
S: Предел функции 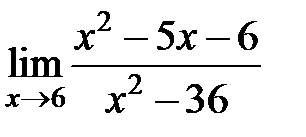 равен ###
равен ###
+: 7/12
I:
S: Предел функции 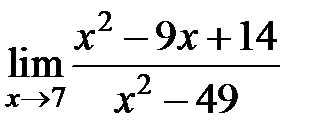 равен ###
равен ###
+: 5/14
I:
S: Предел функции 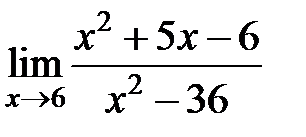 равен ###
равен ###
+: 7/12
I:
S: Предел функции 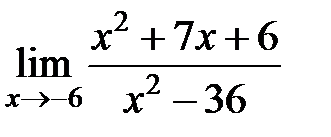 равен ###
равен ###
+: 5/12
I:
S: Предел функции 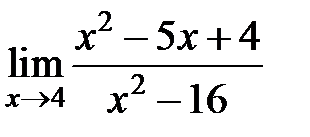 равен ###
равен ###
+: 3/8
I:
S: Предел функции 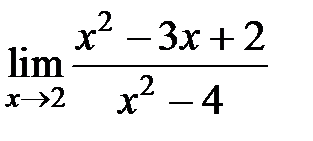 равен ###
равен ###
+:1/4
I:
S: Предел функции 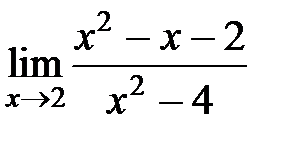 равен ###
равен ###
+: 3/4
I:
S: Предел функции 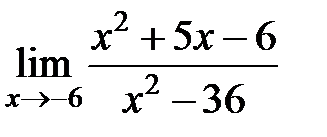 равен ###
равен ###
+: 7/12
I:
S: Предел функции 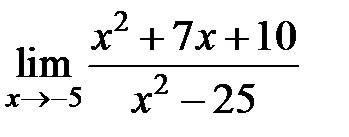 равен ###
равен ###
+: 3/10
I:
S: Предел функции 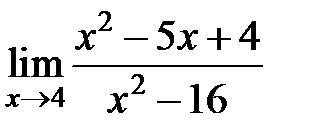 равен ###
равен ###
+: 3/8
I:
S: Предел функции 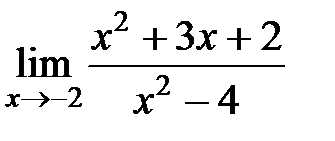 равен ###
равен ###
+: 1/4
I:
S: Предел функции 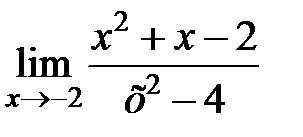 равен ###
равен ###
+: 3/4
I:
S: Предел функции 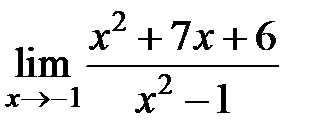 равен ###
равен ###
+: -5/2
I:
S: Предел функции 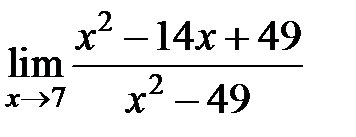 равен ###
равен ###
+: 0
I:
S: Предел функции 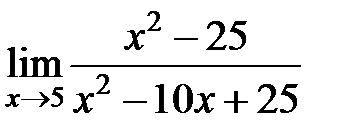 равен ###
равен ###
+: бесконечность
I:
S: Предел функции 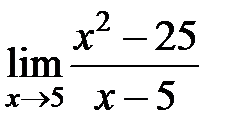 равен ###
равен ###
+: 10
I:
S: Предел функции 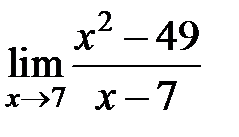 равен ###
равен ###
+: 14
I:
S: Предел функции 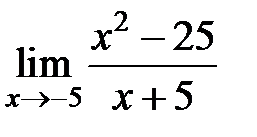 равен ###
равен ###
+: -10
I:
S: Предел функции 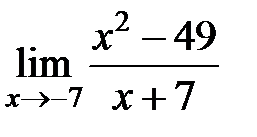 равен ###
равен ###
+: -14
I:
S: Предел функции 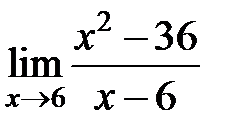 равен ###
равен ###
+: 12
I:
S: Предел функции 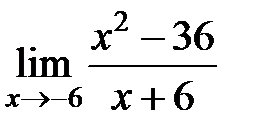 равен ###
равен ###
+: -12
I:
S: Предел функции 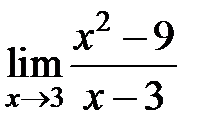 равен ###
равен ###
+: 6
I:
S: Предел функции 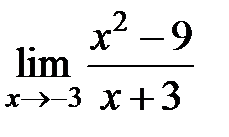 равен ###
равен ###
+: -6
I:
S: Предел функции 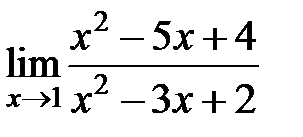 равен ###
равен ###
+: 3
I:
S: Предел функции 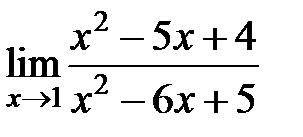 равен ###
равен ###
+: 3/4
I:
S: Предел функции 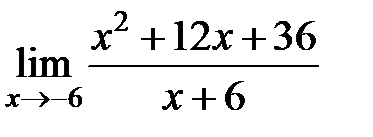 равен ###
равен ###
+: 0
I:
S: Предел функции 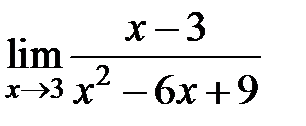 равен ###
равен ###
+: бесконечность
I:
S: Предел функции 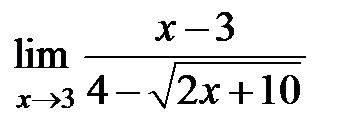 равен ###
равен ###
+: -4
I:
S: Предел функции 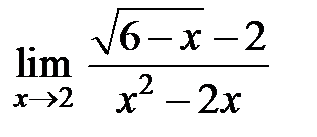 равен ###
равен ###
+: -1/8
I:
S: Предел функции 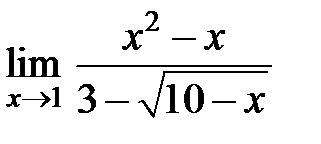 равен ###
равен ###
+: 6
I:
S: Предел функции 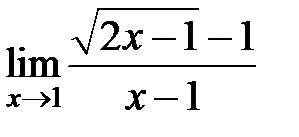 равен ###
равен ###
+: 1
I:
S: Предел функции 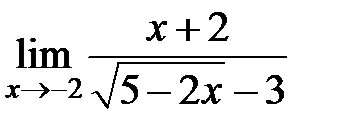 равен ###
равен ###
+: -3
I:
S: Предел функции 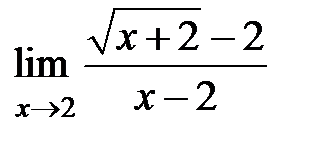 равен ###
равен ###
+: 1/4
I:
S: Предел функции 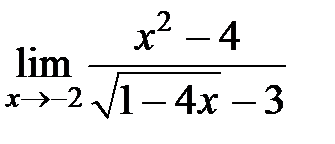 равен ###
равен ###
+: 6
I:
S: Предел функции 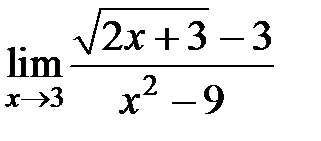 равен ###
равен ###
+: 1/18
I:
S: Предел функции 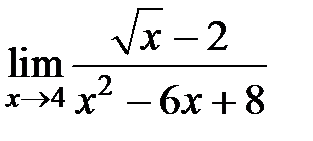 равен ###
равен ###
+: 1/8
I:
S: Предел функции 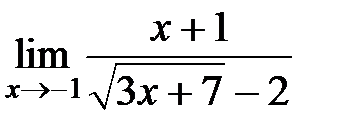 равен ###
равен ###
+: 4/3
I:
S: Предел функции 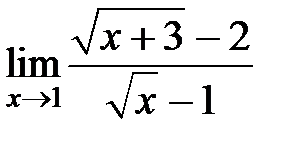 равен ###
равен ###
+: 1/2
I:
S: Предел функции 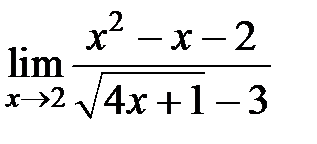 равен ###
равен ###
+: 9/2
I:
S: Предел функции 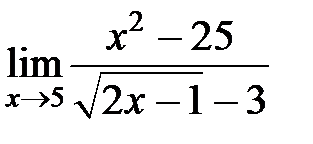 равен ###
равен ###
+: 30
I:
S: Предел функции 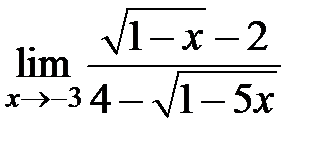 равен ###
равен ###
+: -2/5
I:
S: Предел функции 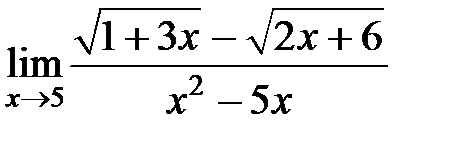 равен ###
равен ###
+: 1/40
I:
S: Предел функции 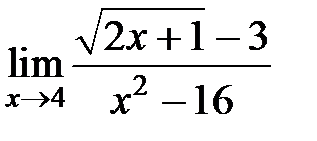 равен ###
равен ###
+: 1/24
I:
S: Предел функции 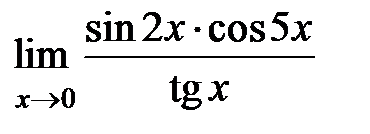 равен ###
равен ###
+: 2
I:
S: Предел функции 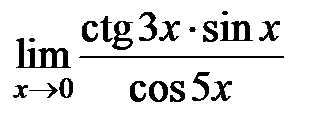 равен ###
равен ###
+: 1/3
I:
S: Предел функции 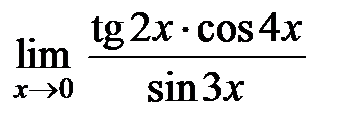 равен ###
равен ###
+: 2/3
I:
S: Предел функции 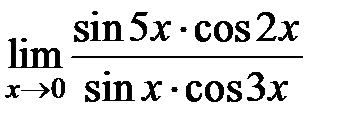 равен ###
равен ###
+: 5
I:
S: Предел функции 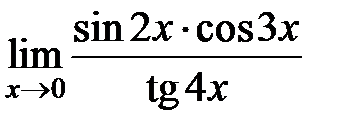 равен ###
равен ###
+: 1/2
I:
S: Предел функции 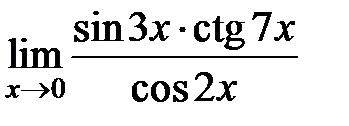 равен ###
равен ###
+: 3/7
I:
S: Предел функции 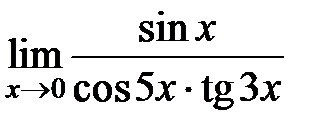 равен ###
равен ###
+: 1/3
I:
S: Предел функции 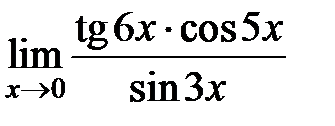 равен ###
равен ###
+: 2
I:
S: Предел функции 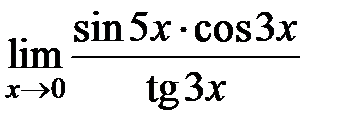 равен ###
равен ###
+: 5/3
I:
S: Предел функции 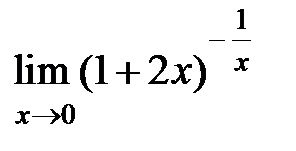 равен ...
равен ...
-: 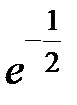
-: 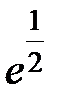
+: 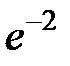
-: 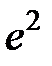
-: 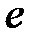
I:
S: Предел функции 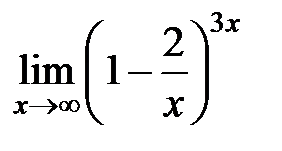 равен ...
равен ...
-: 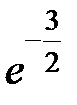
-: 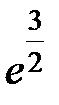
+: 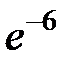
-: 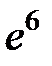
-: 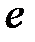
I:
S: Предел функции 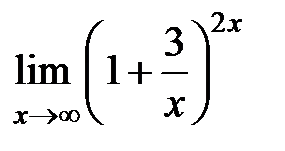 равен ...
равен ...
-: 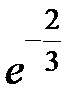
-: 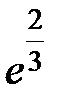
-: 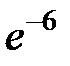
+: 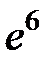
-: 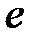
I:
S: Предел функции 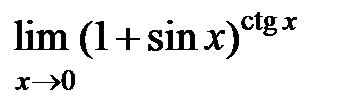 равен ...
равен ...
-: 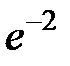
-: 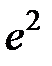
-: 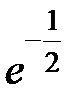
-: 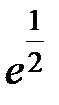
+: 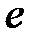
I:
S: Предел функции 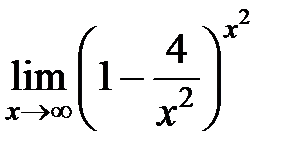 равен ...
равен ...
-: 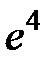
+: 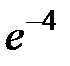
-: 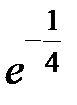
-: 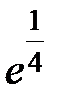
-: 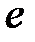
I:
S: Предел функции 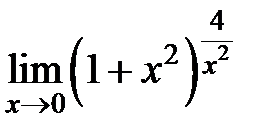 равен ...
равен ...
+: 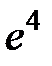
-: 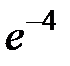
-: 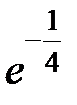
-: 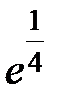
-: 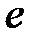
I:
S: Предел функции 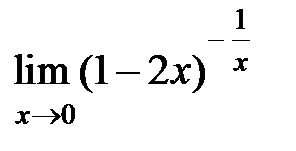 равен ...
равен ...
-: 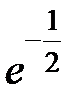
-: 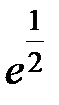
-: 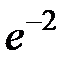
+: 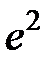
-: 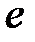
I:
S: Предел функции 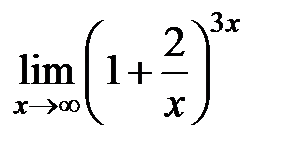 равен ...
равен ...
-: 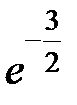
-: 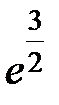
-: 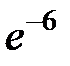
+: 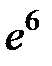
-: 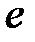
I:
S: Предел функции 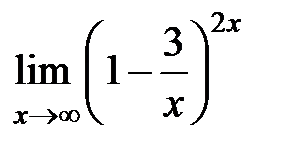 равен ...
равен ...
-: 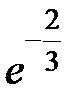
-: 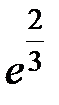
+: 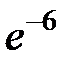
-: 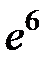
-: 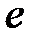
I:
S: Предел функции 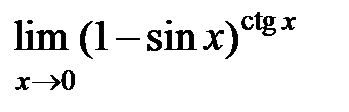 равен ...
равен ...
-: 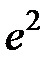
-: 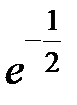
-: 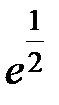
-: 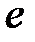
+: 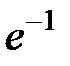
I:
S: Предел функции 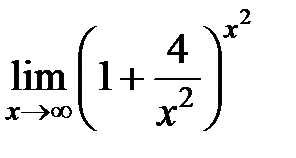 равен ...
равен ...
-: 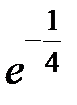
-: 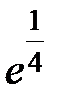
+: 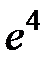
-: 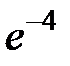
-: 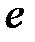
I:
S: Предел функции 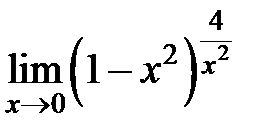 равен ...
равен ...
-: 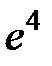
+: 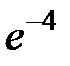
-: 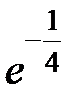
-: 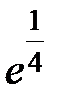
-: 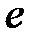
V2: Интегральное исчисление
V3: Неопределенный интеграл
I:
S: Множество первообразных функции 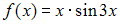 описывается соотношением …
описывается соотношением …
-: 
+: 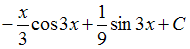
-: 
-: 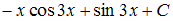
I:
S: Первообразными функции 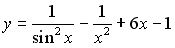 являются …
являются …
+: 
-: 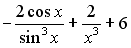
+: 
-: 
+: 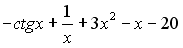
I:
S: Первообразными функции 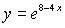 являются…
являются…
-: 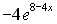
+: 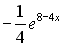
+: 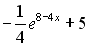
-: 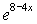
I:
S: Первообразными функции 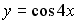 являются…
являются…
-: 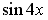
+: 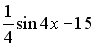
+: 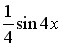
-: 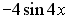
I:
S: Первообразными функции 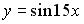 являются…
являются…
-: 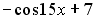
+: 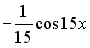
+: 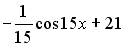
-: 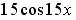
I:
S: Первообразными функции 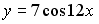 являются…
являются…
-: 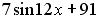
+: 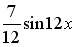
-: 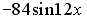
+: 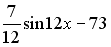
V3: Определенный интеграл
I:
S: Среднее значение функции 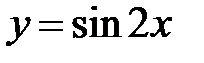 на отрезке
на отрезке 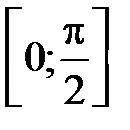 равно …
равно …
-: 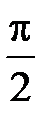
-: 1
+: 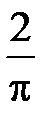
-: 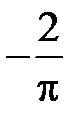
I:
S: Среднее значение функции 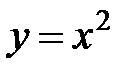 на отрезке
на отрезке 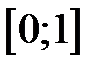 равно …
равно …
-: 
-: 1
+: 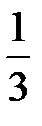
-: 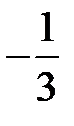
I:
S: Среднее значение функции 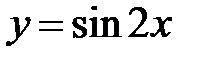 на отрезке
на отрезке  равно …
равно …
-: 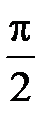
+: 0
-: 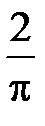
-: 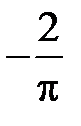
I:
S: Среднее значение функции 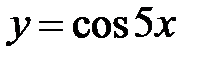 на отрезке
на отрезке 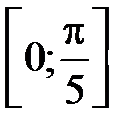 равно …
равно …
-: 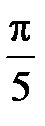
-: 1
-: 
+: 0
I:
S: Среднее значение функции 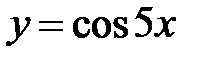 на отрезке
на отрезке 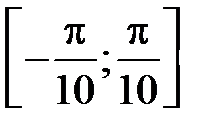 равно …
равно …
-: 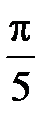
-: 0
+: 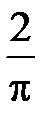
-: 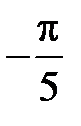
I:
S: Определенный интеграл 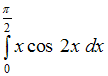 равен …
равен …
+: – 0.5
-: 0.5
-: 0
-: – 2
I:
S: Определенный интеграл 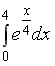 равен…
равен…
-: 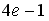
+: 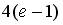
-: 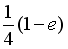
-: 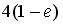
I:
S: Определенный интеграл 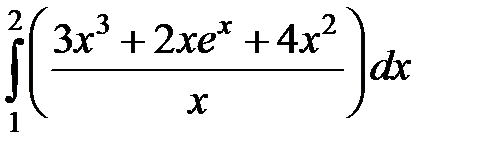 равен…
равен…
-: 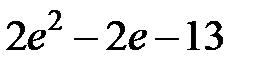
+: 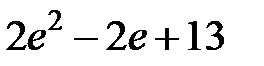
-: 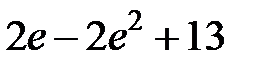
-: 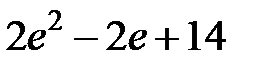
I:
S: Объем тела, образованного вращением вокруг оси 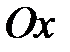 фигуры, ограниченной параболой
фигуры, ограниченной параболой  и осью
и осью 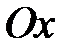 , равен …
, равен …
-: 
+: 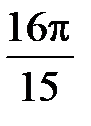
-: 
-: 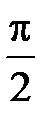
I:
S: Объем тела, образованного вращением вокруг оси 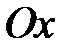 фигуры, ограниченной параболами
фигуры, ограниченной параболами 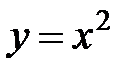 и
и  , равен …
, равен …
-: 
-: 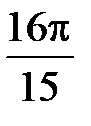
-: 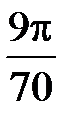
+: 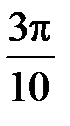
I:
V3: Несобственные интегралы
I:
S: Несобственный интеграл обозначается:
-: 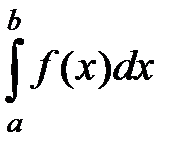
+: 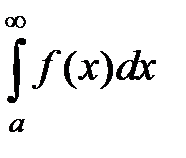
+: 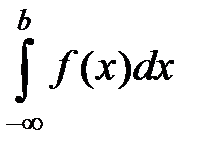
-: 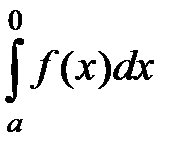
+: 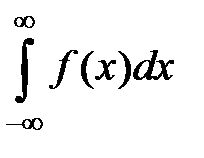
I:
S: Несобственным интегралом называется:
-: 
+: 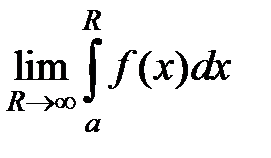
+: 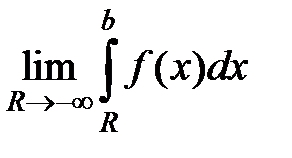
-: 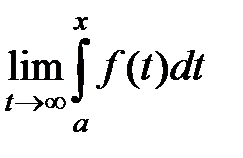
I:
S: Несобственный интеграл 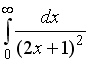 равен …
равен …
+: 0.5
-: 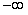
-: -0.5
-: 4
I:
S: Несобственный интеграл 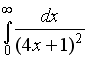 равен …
равен …
+: 0.25
-: - 0.25
-: 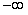
-: 8
I:
S: Несобственный интеграл 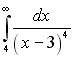 равен …
равен …
-: 4
-: 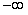
+: 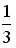
-: 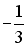
I:
S: Сходящимися являются несобственные интегралы …
-: 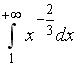
+: 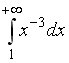
-: 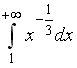
+: 
I:
S: Сходящимися являются несобственные интегралы …
-: 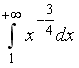
+: 
-: 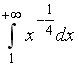
+: 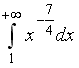
I:
S: Сходящимися являются несобственные интегралы …
-: 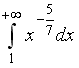
-: 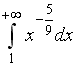
+: 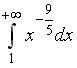
+: 
I:
S: Сходящимися являются несобственные интегралы …
+: 
-: 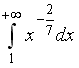
-: 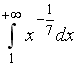
+: 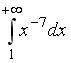
I:
S: Сходящимися являются несобственные интегралы …
-: 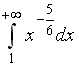
-: 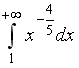
+: 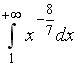
+: 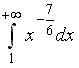
КАЗАНСКИЙ КООПЕРАТИВНЫЙ ИНСТИТУТ (ФИЛИАЛ)
УТВЕРЖДАЮ
 Проректор по учебной работе
Проректор по учебной работе
А.Р. Набиева
«09» сентября 2016 года
Математика
Дата: 2019-02-25, просмотров: 405.