
Ортонормированный базис.

Скалярное произведение.

Определение, свойства, скалярный квадрат. 
Скалярное произведение в ортонормированном базисе, модуль,
Направляющие косинусы, угол между векторами,
условие ортогональности двух векторов.
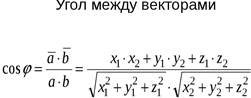

Векторное произведение, определение, свойства.


Векторное произведение в ортонормированном базисе.
Смешанное произведение векторов, определение,
Геометрический смысл. Смешанное произведение
В ортонормированном базисе, свойства произведения.

Условие компланарности трех векторов.

Аналитическая геометрия на плоскости
Радиус-вектор точки.
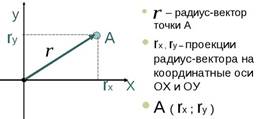
Координаты точки.

Простейшие задачи аналитической геометрии:
координаты вектора, расстояние между точками,
Деление отрезка в данном отношении.

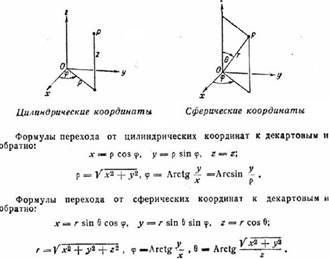
Полярная, цилиндрическая и сферическая системы координат.
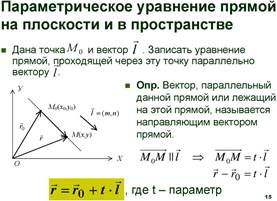
Уравнение линии на плоскости, параметрические уравнения.
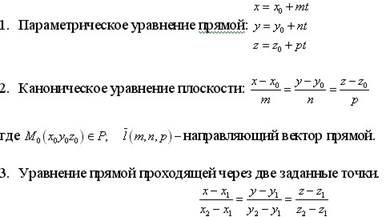
Уравнения поверхности и линии в пространстве,
параметрические уравнения поверхности и линии.
Пересечение поверхностей. Классификация поверхностей.
Алгебраические уравнения 1-го порядка.
Прямая линия на плоскости, векторные уравнения
прямой, общее уравнение, параметрические уравнения,
Канонические уравнения.
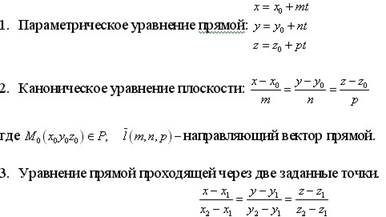
Уравнения прямой с угловым коэффициентом.
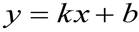
Взаимное расположение двух прямых, угол между прямыми,
условия параллельности и ортогональности.

Расстояние от точки до прямой. Пучок прямых.

Аналитическая геометрия в пространстве
Плоскость в пространстве. Векторное и общее уравнение плоскости.

Векторное уравнение прямой.

Взаимное расположение двух плоскостей.
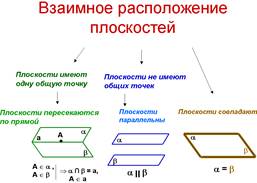
Расстояние от точки до плоскости.

Прямая в пространстве. Общее уравнение,
векторное уравнение, параметрические уравнения, канонические уравнения. 
Приведение общих уравнений к каноническому виду.
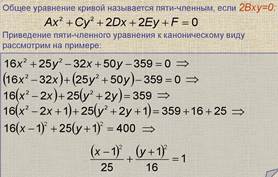
Взаимное расположение двух прямых.
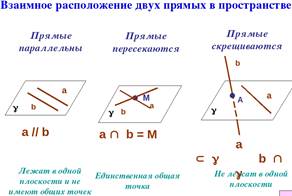
Расстояние между двумя прямыми, условие пересечения прямых.

Прямая и плоскость в пространстве, взаимное расположение. 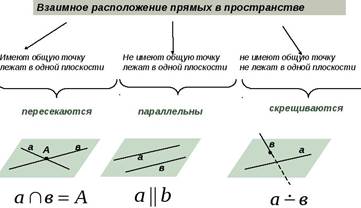
Пучок плоскостей.

Линии 2-го порядка на плоскости. Каноническое уравнение эллипса, гиперболы.
Каноническое уравнение параболы.
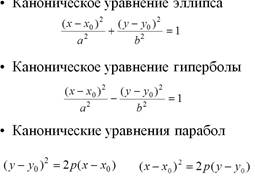
Преобразование координат на плоскости.

Исследование общего уравнения кривой второго порядка.

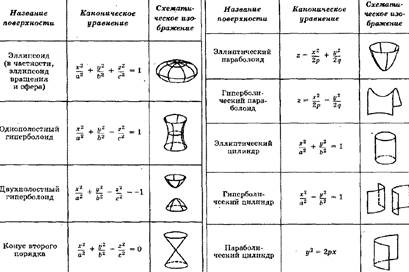
Поверхности 2-го порядка, канонические
уравнения эллипсоида, гиперболоидов, параболоидов.


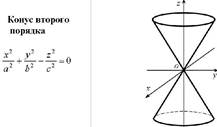
Цилиндрические конические поверхности. Цилиндры и конусы 2-го порядка.
Метод сечений исследования поверхностей.

Матрицы, определители, системы алгебраических уравнений
Матрицы, определение, обозначение, различные виды матриц.

Дата: 2019-02-25, просмотров: 422.