Прямая задача состоит в том, чтобы по известным параметрам исходного звена рассчитать и назначить соответствующие параметры всех составляющих звеньев. Эту задачу ещё называют проектной, т.к. её решают главным образом при проектировании машины или технологического процесса.

Конструктор, при проектировании машины, исходя из обеспечения требуемого показателя точности машины, который является исходным звеном РЦ, рассчитывает и назначает обоснованные допуски на детали, являющиеся составляющими звенья РЦ. Технолог, при разработке ТП в результате расчёта РЦ, в которой исходным звеном является получаемый размер на детали выбирает и назначает требуемую точность технологического оборудования, оснастки, инструмента, средств контроля. Метролог при разработке схем измерения показателей точности в результате решения прямой задачи в измерительной РЦ выбирает и назначает требуемую точность измерительных инструментов и устройств.

Особенностью решения прямой задачи является её многовариантность. Для каждого из составляющих звеньев можно назначить множество комбинаций исходных величин. При выборе из этого множества решений, подходящего для решаемой конкретной задачи, приходится использовать дополнительные критерии:

- физическая возможность назначаемой точности допуска в условиях реального производства;

- затраты на достижение назначаемой точности на всех составляющих звеньев.

Оптимальным считается такое решение, которое обеспечивает минимальные затраты в производстве на изготовление деталей с задаваемой по этому решению точностью. Таким образом, прямая задача в РЦ всегда представляет собой задачу технико-экономическую.

Обратная задача состоит в том, что по известным параметрам составляющих звеньев РЦ необходимо определить параметры замыкающего звена. Эту задачу называют ещё проверочной, т.к. конструктор с её помощью проверяет правильность назначенных в ходе решения прямой задачи допусков на составляющие звенья РЦ. Технолог решением обратной задачи в технологической РЦ проверяет возможность получения на детали заданной точности допуска при использовании уже имеющихся в цехе оборудования, оснастки и инструмента.

Основные уравнения.

Найдем зависимости между основными параметрами замыкающего звена и составляющих звеньев плоской размерной цепи с параллельными звеньями. Очевидно, что номинальное значение замыкающего звена А_D составит

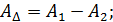
В общем случае при n увеличивающих и p уменьшающих звеньев в размерной цепи получим:

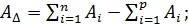                                                                 (1)

Это уравнение принято называть уравнением размерной цепи или уравнением номиналов.

Используя понятие передаточного отношения x_i, которое равно +1 для увеличивающих и –1 для уменьшающих звеньев, уравнение размерной цепи можно записать в более компактной форме

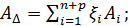                                                                             (2)

Очевидно, что наибольшее и наименьшее предельные значения замыкающего звена А_D выразятся через предельные значения составляющих звеньев А₁ и А₂ следующим образом:

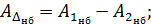
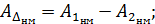
В общем случае

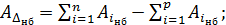                                                         (3)

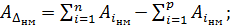                                                         (4)

Для установления зависимости между допуском замыкающего звена и допусками составляющих звеньев размерной цепи вычтем почленно из уравнения (3) уравнение (4). При этом получим:

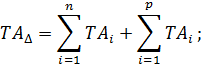
или окончательно

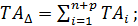                                                                           (5)

т. е. допуск замыкающего звена равен сумме допусков составляющих звеньев.

Найдем зависимости между предельными отклонениями замыкающего звена и составляющих звеньев размерной цепи. Верхнее отклонение замыкающего звена равно разности сумм верхних отклонений увеличивающих звеньев и нижних отклонений уменьшающих звеньев, а нижнее отклонение замыкающего звена равно разности сумм нижних отклонений увеличивающих звеньев и верхних отклонений уменьшающих звеньев.

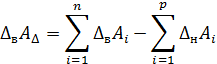
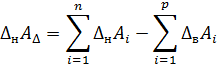
Установим зависимость между координатой середины поля допуска замыкающего звена (D₀A_D) и координатами середин полей допусков составляющих звеньев (D₀A_i).

Координата середины поля допуска замыкающего звена равна разности сумм координат середин полей допусков увеличивающих и уменьшающих звеньев.

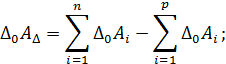
или

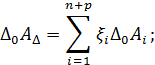
Выразим среднее значение замыкающего звена (A_Dср) через средние значения составляющих звеньев A_iср).

Среднее значение замыкающего звена равно разности сумм средних значений увеличивающих и уменьшающих звеньев.

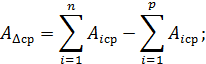
или

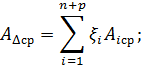
Предполагается, что в размерной цепи возможно одновременное сочетание наибольших увеличивающих и наименьших уменьшающих звеньев или их обратное сочетание. Метод расчета размерных цепей, основанный на использовании этих зависимостей, получил название метода максимума-минимума. Он обеспечивает полную взаимозаменяемость, исключая появление брака.