Рабочая программа по алгебре

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Рабочая программа по алгебре

Для 8 «а», 8 «б» классов

Рабочая программа составлена на основе авторской программы:

Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала математического анализа. 10-11 классы / авт.-сост. И.И. Зубарева, А.Г. Мордкович.

– М.: Мнемозина, 2011.

Учебник: Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович. – М.: Мнемозина, 2013.

Составитель: Фрицлер Анатолий Александрович,

Учитель математики

Первая квалификационная категория

2015 год

Пояснительная записка

1.1. Нормативно-правовое и учебно-методическое обеспечение образовательного процесса:

Рабочая программа составлена на основе:

ü Федерального государственного образовательного стандарта основного общего образования, утвержденного приказом Министерства образования и науки Российской Федерации № 1897 от 17.12.2010 г. «Об утверждении федерального государственного образовательного стандарта основного общего образования»;

ü Фундаментального ядра содержания общего образования;

ü Примерной основной образовательной программы основного общего образования;

ü Примерной программы по математике 5-9 классов;

ü Авторской программы «И.И. Зубарева, А.Г. Мордкович. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала математического анализа. 10-11 классы».

Компоненты УМК:

ü Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович. – М.: Мнемозина, 2013.

ü Алгебра. 8 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / [А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. – М.: Мнемозина, 2013.

ü Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала математического анализа. 10-11 классы / авт.-сост. И.И. Зубарева, А.Г. Мордкович. – М.: Мнемозина, 2011

ü Алгебра. 8 класс: методическое пособие для учителя / А.Г. Мордкович. – М.: Мнемозина, 2013

Цели, задачи преподавания учебного предмета

Обучение алгебре по данной программе направлено на достижение следующих целей:

В направлении личностного развития:

- развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;

- формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;

- воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;

- формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

- развитие интереса к математическому творчеству;

- развитие математических способностей;

2) в метапредметном направлении:

- развитие представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;

- развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;

- формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;

3) в предметном направлении:

- овладение алгебраическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных образовательных организациях, для изучения смежных дисциплин, применения в повседневной жизни;

- создание фундамента математического развития, формирования механизмов мышления, характерных для математической деятельности.

Метапредметные результаты освоения учебного предмета

В соответствии ФГОС ООО выделяются три группы универсальных учебных действий: регулятивные, познавательные, коммуникативные.

Регулятивные УУД

1. Умение самостоятельно определять цели обучения, ставить и формулировать новые задачи в учебе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности. Обучающийся сможет:

· анализировать существующие и планировать будущие образовательные результаты;

· идентифицировать собственные проблемы и определять главную проблему;

· выдвигать версии решения проблемы, формулировать гипотезы, предвосхищать конечный результат;

· ставить цель деятельности на основе определенной проблемы и существующих возможностей;

· формулировать учебные задачи как шаги достижения поставленной цели деятельности;

· обосновывать целевые ориентиры и приоритеты ссылками на ценности, указывая и обосновывая логическую последовательность шагов.

2. Умение самостоятельно планировать пути достижения целей, в том числе альтернативные, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Обучающийся сможет:

· определять необходимые действие(я) в соответствии с учебной и познавательной задачей и составлять алгоритм их выполнения;

· обосновывать и осуществлять выбор наиболее эффективных способов решения учебных и познавательных задач;

· определять/находить, в том числе из предложенных вариантов, условия для выполнения учебной и познавательной задачи;

· выстраивать жизненные планы на краткосрочное будущее (заявлять целевые ориентиры, ставить адекватные им задачи и предлагать действия, указывая и обосновывая логическую последовательность шагов);

· выбирать из предложенных вариантов и самостоятельно искать средства/ресурсы для решения задачи/достижения цели;

· составлять план решения проблемы (выполнения проекта, проведения исследования);

· определять потенциальные затруднения при решении учебной и познавательной задачи и находить средства для их устранения;

· описывать свой опыт, оформляя его для передачи другим людям в виде технологии решения практических задач определенного класса;

· планировать и корректировать свою индивидуальную образовательную траекторию.

3. Умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией. Обучающийся сможет:

· определять совместно с педагогом и сверстниками критерии планируемых результатов и критерии оценки своей учебной деятельности;

· систематизировать (в том числе выбирать приоритетные) критерии планируемых результатов и оценки своей деятельности;

· отбирать инструменты для оценивания своей деятельности, осуществлять самоконтроль своей деятельности в рамках предложенных условий и требований;

· оценивать свою деятельность, аргументируя причины достижения или отсутствия планируемого результата;

· находить достаточные средства для выполнения учебных действий в изменяющейся ситуации и/или при отсутствии планируемого результата;

· работая по своему плану, вносить коррективы в текущую деятельность на основе анализа изменений ситуации для получения запланированных характеристик продукта/результата;

· устанавливать связь между полученными характеристиками продукта и характеристиками процесса деятельности и по завершении деятельности предлагать изменение характеристик процесса для получения улучшенных характеристик продукта;

· сверять свои действия с целью и, при необходимости, исправлять ошибки самостоятельно.

4. Умение оценивать правильность выполнения учебной задачи, собственные возможности ее решения. Обучающийся сможет:

· определять критерии правильности (корректности) выполнения учебной задачи;

· анализировать и обосновывать применение соответствующего инструментария для выполнения учебной задачи;

· свободно пользоваться выработанными критериями оценки и самооценки, исходя из цели и имеющихся средств, различая результат и способы действий;

· оценивать продукт своей деятельности по заданным и/или самостоятельно определенным критериям в соответствии с целью деятельности;

· обосновывать достижимость цели выбранным способом на основе оценки своих внутренних ресурсов и доступных внешних ресурсов;

· фиксировать и анализировать динамику собственных образовательных результатов.

5. Владение основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной деятельности. Обучающийся сможет:

· наблюдать и анализировать собственную учебную и познавательную деятельность и деятельность других обучающихся в процессе взаимопроверки;

· соотносить реальные и планируемые результаты индивидуальной образовательной деятельности и делать выводы;

· принимать решение в учебной ситуации и нести за него ответственность;

· самостоятельно определять причины своего успеха или неуспеха и находить способы выхода из ситуации неуспеха;

· ретроспективно определять, какие действия по решению учебной задачи или параметры этих действий привели к получению имеющегося продукта учебной деятельности;

· демонстрировать приемы регуляции психофизиологических/ эмоциональных состояний для достижения эффекта успокоения (устранения эмоциональной напряженности), эффекта восстановления (ослабления проявлений утомления), эффекта активизации (повышения психофизиологической реактивности).

Познавательные УУД

6. Умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное, по аналогии) и делать выводы. Обучающийся сможет:

· подбирать слова, соподчиненные ключевому слову, определяющие его признаки и свойства;

· выстраивать логическую цепочку, состоящую из ключевого слова и соподчиненных ему слов;

· выделять общий признак двух или нескольких предметов или явлений и объяснять их сходство;

· объединять предметы и явления в группы по определенным признакам, сравнивать, классифицировать и обобщать факты и явления;

· выделять явление из общего ряда других явлений;

· определять обстоятельства, которые предшествовали возникновению связи между явлениями, из этих обстоятельств выделять определяющие, способные быть причиной данного явления, выявлять причины и следствия явлений;

· строить рассуждение от общих закономерностей к частным явлениям и от частных явлений к общим закономерностям;

· строить рассуждение на основе сравнения предметов и явлений, выделяя при этом общие признаки;

· излагать полученную информацию, интерпретируя ее в контексте решаемой задачи;

· самостоятельно указывать на информацию, нуждающуюся в проверке, предлагать и применять способ проверки достоверности информации;

· вербализовать эмоциональное впечатление, оказанное на него источником;

· объяснять явления, процессы, связи и отношения, выявляемые в ходе познавательной и исследовательской деятельности (приводить объяснение с изменением формы представления; объяснять, детализируя или обобщая; объяснять с заданной точки зрения);

· выявлять и называть причины события, явления, в том числе возможные /наиболее вероятные причины, возможные последствия заданной причины, самостоятельно осуществляя причинно-следственный анализ;

· делать вывод на основе критического анализа разных точек зрения, подтверждать вывод собственной аргументацией или самостоятельно полученными данными.

7. Умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач. Обучающийся сможет:

· обозначать символом и знаком предмет и/или явление;

· определять логические связи между предметами и/или явлениями, обозначать данные логические связи с помощью знаков в схеме;

· создавать абстрактный или реальный образ предмета и/или явления;

· строить модель/схему на основе условий задачи и/или способа ее решения;

· создавать вербальные, вещественные и информационные модели с выделением существенных характеристик объекта для определения способа решения задачи в соответствии с ситуацией;

· преобразовывать модели с целью выявления общих законов, определяющих данную предметную область;

· переводить сложную по составу (многоаспектную) информацию из графического или формализованного (символьного) представления в текстовое, и наоборот;

· строить схему, алгоритм действия, исправлять или восстанавливать неизвестный ранее алгоритм на основе имеющегося знания об объекте, к которому применяется алгоритм;

· строить доказательство: прямое, косвенное, от противного;

· анализировать/рефлексировать опыт разработки и реализации учебного проекта, исследования (теоретического, эмпирического) на основе предложенной проблемной ситуации, поставленной цели и/или заданных критериев оценки продукта/результата.

8. Смысловое чтение. Обучающийся сможет:

· находить в тексте требуемую информацию (в соответствии с целями своей деятельности);

· ориентироваться в содержании текста, понимать целостный смысл текста, структурировать текст;

· устанавливать взаимосвязь описанных в тексте событий, явлений, процессов;

· резюмировать главную идею текста;

· преобразовывать текст, «переводя» его в другую модальность, интерпретировать текст (художественный и нехудожественный – учебный, научно-популярный, информационный, текст non-fiction);

· критически оценивать содержание и форму текста.

9. Формирование и развитие экологического мышления, умение применять его в познавательной, коммуникативной, социальной практике и профессиональной ориентации. Обучающийся сможет:

· определять свое отношение к природной среде;

· анализировать влияние экологических факторов на среду обитания живых организмов;

· проводить причинный и вероятностный анализ экологических ситуаций;

· прогнозировать изменения ситуации при смене действия одного фактора на действие другого фактора;

· распространять экологические знания и участвовать в практических делах по защите окружающей среды;

· выражать свое отношение к природе через рисунки, сочинения, модели, проектные работы.

10. Развитие мотивации к овладению культурой активного использования словарей и других поисковых систем. Обучающийся сможет:

· определять необходимые ключевые поисковые слова и запросы;

· осуществлять взаимодействие с электронными поисковыми системами, словарями;

· формировать множественную выборку из поисковых источников для объективизации результатов поиска;

· соотносить полученные результаты поиска со своей деятельностью.

Коммуникативные УУД

11. Умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; работать индивидуально и в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; формулировать, аргументировать и отстаивать свое мнение. Обучающийся сможет:

- определять возможные роли в совместной деятельности;

- играть определенную роль в совместной деятельности;

- принимать позицию собеседника, понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории;

- определять свои действия и действия партнера, которые способствовали или препятствовали продуктивной коммуникации;

- строить позитивные отношения в процессе учебной и познавательной деятельности;

- корректно и аргументированно отстаивать свою точку зрения, в дискуссии уметь выдвигать контраргументы, перефразировать свою мысль (владение механизмом эквивалентных замен);

- критически относиться к собственному мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его;

- предлагать альтернативное решение в конфликтной ситуации;

- выделять общую точку зрения в дискуссии;

- договариваться о правилах и вопросах для обсуждения в соответствии с поставленной перед группой задачей;

- организовывать учебное взаимодействие в группе (определять общие цели, распределять роли, договариваться друг с другом и т. д.);

- устранять в рамках диалога разрывы в коммуникации, обусловленные непониманием/неприятием со стороны собеседника задачи, формы или содержания диалога.

12. Умение осознанно использовать речевые средства в соответствии с задачей коммуникации для выражения своих чувств, мыслей и потребностей для планирования и регуляции своей деятельности; владение устной и письменной речью, монологической контекстной речью. Обучающийся сможет:

· определять задачу коммуникации и в соответствии с ней отбирать речевые средства;

· отбирать и использовать речевые средства в процессе коммуникации с другими людьми (диалог в паре, в малой группе и т. д.);

· представлять в устной или письменной форме развернутый план собственной деятельности;

· соблюдать нормы публичной речи, регламент в монологе и дискуссии в соответствии с коммуникативной задачей;

· высказывать и обосновывать мнение (суждение) и запрашивать мнение партнера в рамках диалога;

· принимать решение в ходе диалога и согласовывать его с собеседником;

· создавать письменные «клишированные» и оригинальные тексты с использованием необходимых речевых средств;

· использовать вербальные средства (средства логической связи) для выделения смысловых блоков своего выступления;

· использовать невербальные средства или наглядные материалы, подготовленные/отобранные под руководством учителя;

· делать оценочный вывод о достижении цели коммуникации непосредственно после завершения коммуникативного контакта и обосновывать его.

13. Формирование и развитие компетентности в области использования информационно-коммуникационных технологий (далее – ИКТ). Обучающийся сможет:

· целенаправленно искать и использовать информационные ресурсы, необходимые для решения учебных и практических задач с помощью средств ИКТ;

· выбирать, строить и использовать адекватную информационную модель для передачи своих мыслей средствами естественных и формальных языков в соответствии с условиями коммуникации;

· выделять информационный аспект задачи, оперировать данными, использовать модель решения задачи;

· использовать компьютерные технологии (включая выбор адекватных задаче инструментальных программно-аппаратных средств и сервисов) для решения информационных и коммуникационных учебных задач, в том числе: вычисление, написание писем, сочинений, докладов, рефератов, создание презентаций и др.;

· использовать информацию с учетом этических и правовых норм;

· создавать информационные ресурсы разного типа и для разных аудиторий, соблюдать информационную гигиену и правила информационной безопасности.

Числа

· Оперировать на базовом уровне понятиями: натуральное число, целое число, обыкновенная дробь, десятичная дробь, смешанная дробь, рациональное число, арифметический квадратный корень;

· использовать свойства чисел и правила действий при выполнении вычислений;

· использовать признаки делимости на 2, 5, 3, 9, 10 при выполнении вычислений и решении несложных задач;

· выполнять округление рациональных чисел в соответствии с правилами;

· оценивать значение квадратного корня из положительного целого числа;

· распознавать рациональные и иррациональные числа;

· сравнивать числа.

В повседневной жизни и при изучении других предметов:

· оценивать результаты вычислений при решении практических задач;

· выполнять сравнение чисел в реальных ситуациях;

· составлять числовые выражения при решении практических задач и задач из других учебных предметов.

Тождественные преобразования

· Выполнять несложные преобразования для вычисления значений числовых выражений, содержащих степени с натуральным показателем, степени с целым отрицательным показателем;

· выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые;

· использовать формулы сокращенного умножения (квадрат суммы, квадрат разности, разность квадратов) для упрощения вычислений значений выражений;

· выполнять несложные преобразования дробно-линейных выражений и выражений с квадратными корнями.

В повседневной жизни и при изучении других предметов:

· понимать смысл записи числа в стандартном виде;

· оперировать на базовом уровне понятием «стандартная запись числа».

Уравнения и неравенства

· Оперировать на базовом уровне понятиями: равенство, числовое равенство, уравнение, корень уравнения, решение уравнения, числовое неравенство, неравенство, решение неравенства;

· проверять справедливость числовых равенств и неравенств;

· решать линейные неравенства и несложные неравенства, сводящиеся к линейным;

· решать системы несложных линейных уравнений, неравенств;

· проверять, является ли данное число решением уравнения (неравенства);

· решать квадратные уравнения по формуле корней квадратного уравнения;

· изображать решения неравенств и их систем на числовой прямой.

В повседневной жизни и при изучении других предметов:

· составлять и решать линейные уравнения при решении задач, возникающих в других учебных предметах.

Функции

· Находить значение функции по заданному значению аргумента;

· находить значение аргумента по заданному значению функции в несложных ситуациях;

· определять положение точки по её координатам, координаты точки по её положению на координатной плоскости;

· по графику находить область определения, множество значений, нули функции, промежутки знакопостоянства, промежутки возрастания и убывания, наибольшее и наименьшее значения функции;

· строить график линейной функции;

· проверять, является ли данный график графиком заданной функции (линейной, квадратичной, обратной пропорциональности);

· определять приближённые значения координат точки пересечения графиков функций;

· оперировать на базовом уровне понятиями: последовательность, арифметическая прогрессия, геометрическая прогрессия;

· решать задачи на прогрессии, в которых ответ может быть получен непосредственным подсчётом без применения формул.

В повседневной жизни и при изучении других предметов:

· использовать графики реальных процессов и зависимостей для определения их свойств (наибольшие и наименьшие значения, промежутки возрастания и убывания, области положительных и отрицательных значений и т.п.);

· использовать свойства линейной функции и ее график при решении задач из других учебных предметов.

Текстовые задачи

· Решать несложные сюжетные задачи разных типов на все арифметические действия;

· строить модель условия задачи (в виде таблицы, схемы, рисунка или уравнения), в которой даны значения двух из трёх взаимосвязанных величин, с целью поиска решения задачи;

· осуществлять способ поиска решения задачи, в котором рассуждение строится от условия к требованию или от требования к условию;

· составлять план решения задачи;

· выделять этапы решения задачи;

· интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи;

· знать различие скоростей объекта в стоячей воде, против течения и по течению реки;

· решать задачи на нахождение части числа и числа по его части;

· решать задачи разных типов (на работу, на покупки, на движение), связывающих три величины, выделять эти величины и отношения между ними;

· находить процент от числа, число по проценту от него, находить процентное снижение или процентное повышение величины;

· решать несложные логические задачи методом рассуждений.

В повседневной жизни и при изучении других предметов:

· выдвигать гипотезы о возможных предельных значениях искомых в задаче величин (делать прикидку).

История математики

· Описывать отдельные выдающиеся результаты, полученные в ходе развития математики как науки;

· знать примеры математических открытий и их авторов, в связи с отечественной и всемирной историей;

· понимать роль математики в развитии России.

Методы математики

· Выбирать подходящий изученный метод для решении изученных типов математических задач;

· Приводить примеры математических закономерностей в окружающей действительности и произведениях искусства.

Выпускник получит возможность научиться в 7-9 классах для обеспечения возможности успешного продолжения образования на базовом и углублённом уровнях

Числа

· Оперировать понятиями: множество натуральных чисел, множество целых чисел, множество рациональных чисел, иррациональное число, квадратный корень, множество действительных чисел, геометрическая интерпретация натуральных, целых, рациональных, действительных чисел;

· понимать и объяснять смысл позиционной записи натурального числа;

· выполнять вычисления, в том числе с использованием приёмов рациональных вычислений;

· выполнять округление рациональных чисел с заданной точностью;

· сравнивать рациональные и иррациональные числа;

· представлять рациональное число в виде десятичной дроби

· упорядочивать числа, записанные в виде обыкновенной и десятичной дроби;

· находить НОД и НОК чисел и использовать их при решении задач.

В повседневной жизни и при изучении других предметов:

· применять правила приближенных вычислений при решении практических задач и решении задач других учебных предметов;

· выполнять сравнение результатов вычислений при решении практических задач, в том числе приближенных вычислений;

· составлять и оценивать числовые выражения при решении практических задач и задач из других учебных предметов;

· записывать и округлять числовые значения реальных величин с использованием разных систем измерения.

Тождественные преобразования

· Оперировать понятиями степени с натуральным показателем, степени с целым отрицательным показателем;

· выполнять преобразования целых выражений: действия с одночленами (сложение, вычитание, умножение), действия с многочленами (сложение, вычитание, умножение);

· выполнять разложение многочленов на множители одним из способов: вынесение за скобку, группировка, использование формул сокращенного умножения;

· выделять квадрат суммы и разности одночленов;

· раскладывать на множители квадратный трёхчлен;

· выполнять преобразования выражений, содержащих степени с целыми отрицательными показателями, переходить от записи в виде степени с целым отрицательным показателем к записи в виде дроби;

· выполнять преобразования дробно-рациональных выражений: сокращение дробей, приведение алгебраических дробей к общему знаменателю, сложение, умножение, деление алгебраических дробей, возведение алгебраической дроби в натуральную и целую отрицательную степень;

· выполнять преобразования выражений, содержащих квадратные корни;

· выделять квадрат суммы или разности двучлена в выражениях, содержащих квадратные корни;

· выполнять преобразования выражений, содержащих модуль.

В повседневной жизни и при изучении других предметов:

· выполнять преобразования и действия с числами, записанными в стандартном виде;

· выполнять преобразования алгебраических выражений при решении задач других учебных предметов.

Уравнения и неравенства

· Оперировать понятиями: уравнение, неравенство, корень уравнения, решение неравенства, равносильные уравнения, область определения уравнения (неравенства, системы уравнений или неравенств);

· решать линейные уравнения и уравнения, сводимые к линейным с помощью тождественных преобразований;

· решать квадратные уравнения и уравнения, сводимые к квадратным с помощью тождественных преобразований;

· решать дробно-линейные уравнения;

· решать простейшие иррациональные уравнения вида , ;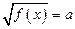

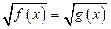· решать уравнения вида ;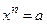

· решать уравнения способом разложения на множители и замены переменной;

· использовать метод интервалов для решения целых и дробно-рациональных неравенств;

· решать линейные уравнения и неравенства с параметрами;

· решать несложные квадратные уравнения с параметром;

· решать несложные системы линейных уравнений с параметрами;

· решать несложные уравнения в целых числах.

В повседневной жизни и при изучении других предметов:

· составлять и решать линейные и квадратные уравнения, уравнения, к ним сводящиеся, системы линейных уравнений, неравенств при решении задач других учебных предметов;

· выполнять оценку правдоподобия результатов, получаемых при решении линейных и квадратных уравнений и систем линейных уравнений и неравенств при решении задач других учебных предметов;

· выбирать соответствующие уравнения, неравенства или их системы для составления математической модели заданной реальной ситуации или прикладной задачи;

· уметь интерпретировать полученный при решении уравнения, неравенства или системы результат в контексте заданной реальной ситуации или прикладной задачи.

Функции

· Оперировать понятиями: функциональная зависимость, функция, график функции, способы задания функции, аргумент и значение функции, область определения и множество значений функции, нули функции, промежутки знакопостоянства, монотонность функции, чётность/нечётность функции;

· строить графики линейной, квадратичной функций, обратной пропорциональности, функции вида: , , , ;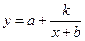

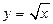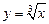
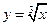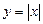· на примере квадратичной функции, использовать преобразования графика функции y = f ( x ) для построения графиков функций ;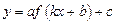

· составлять уравнения прямой по заданным условиям: проходящей через две точки с заданными координатами, проходящей через данную точку и параллельной данной прямой;

· исследовать функцию по её графику;

· находить множество значений, нули, промежутки знакопостоянства, монотонности квадратичной функции;

· оперировать понятиями: последовательность, арифметическая прогрессия, геометрическая прогрессия;

· решать задачи на арифметическую и геометрическую прогрессию.

В повседневной жизни и при изучении других предметов:

· иллюстрировать с помощью графика реальную зависимость или процесс по их характеристикам;

· использовать свойства и график квадратичной функции при решении задач из других учебных предметов.

Текстовые задачи

· Решать простые и сложные задачи разных типов, а также задачи повышенной трудности;

· использовать разные краткие записи как модели текстов сложных задач для построения поисковой схемы и решения задач;

· различать модель текста и модель решения задачи, конструировать к одной модели решения несложной задачи разные модели текста задачи;

· знать и применять оба способа поиска решения задач (от требования к условию и от условия к требованию);

· моделировать рассуждения при поиске решения задач с помощью граф-схемы;

· выделять этапы решения задачи и содержание каждого этапа;

· уметь выбирать оптимальный метод решения задачи и осознавать выбор метода, рассматривать различные методы, находить разные решения задачи, если возможно;

· анализировать затруднения при решении задач;

· выполнять различные преобразования предложенной задачи, конструировать новые задачи из данной, в том числе обратные;

· интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи;

· анализировать всевозможные ситуации взаимного расположения двух объектов и изменение их характеристик при совместном движении (скорость, время, расстояние) при решении задач на движение двух объектов как в одном, так и в противоположных направлениях;

· исследовать всевозможные ситуации при решении задач на движение по реке, рассматривать разные системы отсчёта;

· решать разнообразные задачи «на части»,

· решать и обосновывать свое решение задач (выделять математическую основу) на нахождение части числа и числа по его части на основе конкретного смысла дроби;

· осознавать и объяснять идентичность задач разных типов, связывающих три величины (на работу, на покупки, на движение). выделять эти величины и отношения между ними, применять их при решении задач, конструировать собственные задач указанных типов;

· владеть основными методами решения задач на смеси, сплавы, концентрации;

· решать задачи на проценты, в том числе, сложные проценты с обоснованием, используя разные способы;

· решать логические задачи разными способами, в том числе, с двумя блоками и с тремя блоками данных с помощью таблиц;

· решать задачи по комбинаторике и теории вероятностей на основе использования изученных методов и обосновывать решение;

· решать несложные задачи по математической статистике;

· овладеть основными методами решения сюжетных задач: арифметический, алгебраический, перебор вариантов, геометрический, графический, применять их в новых по сравнению с изученными ситуациях.

В повседневной жизни и при изучении других предметов:

· выделять при решении задач характеристики рассматриваемой в задаче ситуации, отличные от реальных (те, от которых абстрагировались), конструировать новые ситуации с учётом этих характеристик, в частности, при решении задач на концентрации, учитывать плотность вещества;

· решать и конструировать задачи на основе рассмотрения реальных ситуаций, в которых не требуется точный вычислительный результат;

· решать задачи на движение по реке, рассматривая разные системы отсчета.

История математики

· Характеризовать вклад выдающихся математиков в развитие математики и иных научных областей;

· понимать роль математики в развитии России.

Методы математики

· Используя изученные методы, проводить доказательство, выполнять опровержение;

· выбирать изученные методы и их комбинации для решения математических задач;

· использовать математические знания для описания закономерностей в окружающей действительности и произведениях искусства;

· применять простейшие программные средства и электронно-коммуникационные системы при решении математических задач.

4.4. Система оценки планируемых результатов на базовом и повышенном уровнях

Основным объектом оценки результатов в соответствии с требованиями ФГОС ООО является способность к решению учебно-познавательных и учебно-практических задач, основанных на изучаемом учебном материале, с использованием способов действий, релевантных содержанию учебных предметов, в том числе метапредметных (познавательных, регулятивных, коммуникативных) действий. Система оценки предметных результатов освоения учебной программы с учётом уровневого подхода, принятого в Стандарте, предполагает выделение базового уровня достижений как точки отсчёта при построении всей системы оценки и организации индивидуальной работы с обучающимися. Реальные достижения обучающихся могут соответствовать базовому уровню, а могут отличаться от него как в сторону превышения, так и в сторону недостижения.

Для описания достижений обучающихся целесообразно установить следующие пять уровней.

Базовый уровень достижений — уровень, который демонстрирует освоение учебных действий с опорной системой знаний в рамках диапазона (круга) выделенных задач. Овладение базовым уровнем является достаточным для продолжения обучения на следующей ступени образования, но не по профильному направлению. Достижению базового уровня соответствует отметка «удовлетворительно» (или отметка «3», отметка «зачтено»).

Превышение базового уровня свидетельствует об усвоении опорной системы знаний на уровне осознанного произвольного овладения учебными действиями, а также о кругозоре, широте (или избирательности) интересов. Целесообразно выделить следующие два уровня, превышающие базовый:

• повышенный уровень достижения планируемых результатов, оценка «хорошо» (отметка «4»);

• высокий уровень достижения планируемых результатов, оценка «отлично» (отметка «5»).

Повышенный и высокий уровни достижения отличаются по полноте освоения планируемых результатов, уровню овладения учебными действиями и сформированностью интересов к данной предметной области.

Индивидуальные траектории обучения обучающихся, демонстрирующих повышенный и высокий уровни достижений, целесообразно формировать с учётом интересов этих обучающихся и их планов на будущее. При наличии устойчивых интересов к учебному предмету и основательной подготовки по нему такие обучающиеся могут быть вовлечены в проектную деятельность по предмету и сориентированы на продолжение обучения в старших классах по данному профилю.

В уровне достижений ниже базового, целесообразно выделить также два уровня:

• пониженный уровень достижений, оценка «неудовлетворительно» (отметка «2»);

• низкий уровень достижений, оценка «плохо» (отметка «1»).

Недостижение базового уровня (пониженный и низкий уровни достижений) фиксируется в зависимости от объёма и уровня освоенного и неосвоенного содержания предмета.

Как правило, пониженный уровень достижений свидетельствует об отсутствии систематической базовой подготовки, о том, что обучающимся не освоено даже и половины планируемых результатов, которые осваивает большинство обучающихся, о том, что имеются значительные пробелы в знаниях, дальнейшее обучение затруднено. При этом обучающийся может выполнять отдельные задания повышенного уровня. Данная группа обучающихся требует специальной диагностики затруднений в обучении, пробелов в системе знаний и оказании целенаправленной помощи в достижении базового уровня.

Низкий уровень освоения планируемых результатов свидетельствует о наличии только отдельных фрагментарных знаний по предмету, дальнейшее обучение практически невозможно. Обучающимся, которые демонстрируют низкий уровень достижений, требуется специальная помощь не только по учебному предмету, но и по формированию мотивации к обучению, развитию интереса к изучаемой предметной области, пониманию значимости предмета для жизни и др. Только наличие положительной мотивации может стать основой ликвидации пробелов в обучении для данной группы обучающихся.

Описанный выше подход применяется в ходе различных процедур оценивания: текущего, промежуточного и итогового.

Решение о достижении или недостижении планируемых результатов или об освоении или неосвоении учебного материала принимается на основе результатов выполнения заданий базового уровня. Китерий достижения/освоения учебного материала задаётся как выполнение не менее 50% заданий базового уровня или получение 50% от максимального балла за выполнение заданий базового уровня.

Оценка знаний и умений учащихся по алгебре.

1. Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.

Основными формами проверки знаний и умений учащихся по алгебре являются письменная самостоятельная, контрольная работа и устный опрос.

При оценке письменных и устных ответов в первую очередь учитываются показанные учащимися знания и умения. Оценка зависит также от наличия и характера погрешностей, допущенных учащимися.

Среди погрешностей выделяются ошибки и недочеты. Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе.

2. К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, не считающихся в программе основными. Недочетами также считаются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения; неаккуратная запись; небрежное выполнение чертежа.

Граница между ошибками и недочетами является в некоторой степени условной. При одних обстоятельствах допущенная учащимися погрешность может рассматриваться учителем как ошибка, в другое время и при других обстоятельствах — как недочет.

3. Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач.

Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты я обоснованные выводы, а его изложение и письменная запись математически грамотны и отличаются последовательностью и аккуратностью.

Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.

4. Оценка ответа учащегося при устном и письменном опросе проводится по пятибалльной системе, т. е. за ответ выставляется одна из отметок: 1 (плохо), 2 (неудовлетворительно), 3 (удовлетворительно), 4 (хорошо), 5 (отлично).

5. Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии учащегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им заданий.

Критерии ошибок

1) К грубым ошибкам относятся ошибки, которые обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять; незнание приемов решения задач, рассматриваемых в учебниках, а также вычислительные ошибки, если они не являются опиской;

2) К негрубым ошибкам относятся: потеря корня или сохранение в ответе постороннего корня; отбрасывание без объяснений одного из них и равнозначные им;

3) К недочетам относятся: нерациональное решение, описки, недостаточность или отсутствие пояснений, обоснований в решениях.

Оценка устных ответов учащихся

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником,

• изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;

• продемонстрировал сформированность и устойчивость используемых при отработке умений и навыков, усвоение ранее изученных сопутствующих вопросов;

• отвечал самостоятельно без наводящих вопросов учителя. Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.

Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;

• допущены один – два недочета при освещении основного содержания ответа, исправленные по замечанию учителя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя.

Отметка «3» ставится в следующих случаях:

• неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала ;

• имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Отметка «1» ставится, если:

• ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.

Оценка письменных самостоятельных и контрольных работ учащихся

Отметка «5» ставится, если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).

Отметка «4» ставится, если:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).

Отметка «3» ставится, если:

• допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что учащийся не владеет

обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если:

• работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

V . Содержание учебного предмета

Неравенства (15 ч.)

Свойства числовых неравенств.

Неравенство с переменной. Решение неравенств с переменной. Линейное неравенство. Равносильные неравенства. Равносильное преобразование неравенства.

Квадратное неравенство. Алгоритм решения квадратного неравенства.

Возрастающая функция. Убывающая функция. Исследование функций на монотонность (с использованием свойств числовых неравенств).

Приближенные значения действительных чисел, погрешность приближения, приближение по недостатку и избытку. Стандартный вид числа.

Глава 5. Неравенства

15 1 Свойства числовых неравенств. Исследование функций на монотонность. Решение линейных неравенств. Решение квадратных неравенств. Приближенные значения действительных чисел. Стандартный вид положительного числа. Знание свойств числовых неравенств, умение иллюстрировать их на координатной прямой, применять при исследовании функции на монотонность, доказательстве и решении неравенств. Умение распознавать линейные и квадратные неравенства, решать их, показывать решение неравенства в виде числового промежутка на числовой прямой. Умение находить приближенные значение числа с недостатком и с избытком, умение прикидывать и примерно оценивать результат. Умение представлять числа в стандартном виде и выполнять арифметические действия с числами, записанными в стандартном виде, использовать запись числа в стандартном виде для выражения размеров объектов, длительности процессов в реальном мире, сравнивать числа, записанные в стандартном виде. УУД Умение ставить цели, планировать свою деятельность, прогнозировать результат, осуществлять самоконтроль и самооценку. Умение читать математический текст и находить информацию в учебнике по заданной теме. Умение проводить наблюдение, сравнение, анализ, исследование, обобщение. Умение работать по правилу и образцу.Умение выполнять прикидку, оценку размера объектов, длительности реальных процессов. Умение осуществлять мини проектную деятельность. Умение вести диалог, умение слушать, аргументировано высказывать свои суждения. Умение взаимодействовать с товарищами по классу в деловой ситуации, работать в паре и группе.

Обобщающее повторение

8 1 Алгебраические дроби. Функция

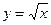. Свойства квадратного корня. Квадратичная функция. Функция

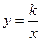. Квадратные уравнения. Неравенства. 8

ИТОГО:

105 10

VII . Поурочное календарно-тематическое планирование

№ урока с начала учебного года

№ урока по теме

Тема урока

Дата проведения урока (план)

Дата проведения урока (факт) 8а класс

Дата проведения урока (факт) 8б класс

Рабочая программа по алгебре

Для 8 «а», 8 «б» классов

Рабочая программа составлена на основе авторской программы:

– М.: Мнемозина, 2011.

Дата: 2019-02-25, просмотров: 196.

12 3 4 5 6 7 8 9 10 Следующая ⇒