Изгибающие моменты в панелях неразрезного верхнего пояса фермы при действии нагрузок, вызывающих в нем максимальные продольные усилия, т.е. при действии нагрузки от собственной массы покрытия и снеговой нагрузки, распределенной на каждом из полупролетов по схеме треугольника, определяем, рассматривая верхний пояс как неразрезную балку, применяя программный комплекс Лира-Windows v. 8.0.
В итоге получаем следующие значения опорных моментов:
;
;
;
.
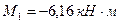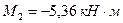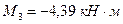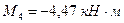| Наименование элемента фермы | Обозначение | Усилия в элементах фермы, кН | |||||
| от постоянной нагрузки (рис. 4.3) | от временной (снеговой) нагрузки | Максимальные | |||||
| равномерной по всему пролету (рис. 4.4, а) | по закону треугольника на каждом полупролете (рис. 4.4, б) | равномерной на 1/2 пролет (рис. 4.4,в) | по закону треугольника на 1/2 пролета (рис. 4.4, в) | ||||
Верхний пояс
O 1
-34.0
-23.1
-23.9
-16.6
-21.1
-58.0
O 2
-31.0
-21.1
-18.1
-13.6
-14.8
-52.0
O 3
-29.6
-20.1
-14.2
-10.1
-9.5
-49.7
O 4
-31.0
-21.1
-14.0
-7.4
-6.6
-52.0
O 5
-34.0
-23.1
-16.3
-6.5
-5.8
-57.1
Нижний пояс
U 1
29.0
19.7
20.4
14.2
18.0
49.5
U 2
29.6
20.1
15.5
12.3
12.0
49.7
U 3
29.6
20.1
12.9
7.8
6.9
49.7
U 4
29.0
19.7
13.9
5.6
5.0
48.8
Раскосы
D 1
0.4
0.3
-4.1
-1.5
-4.9
-4.4
D 2
-0.3
-0.2
2.9
1.1
3.5
3.2
D 3
0.0
0.0
-1.9
-3.4
-3.8
-3.8
D 4
0.0
0.0
1.9
3.4
3.8
3.8
D 5
-0.3
-0.2
0.6
-1.3
-1.2
-1.6
D 6
0.4
0.3
-0.8
1.8
1.6
2.1
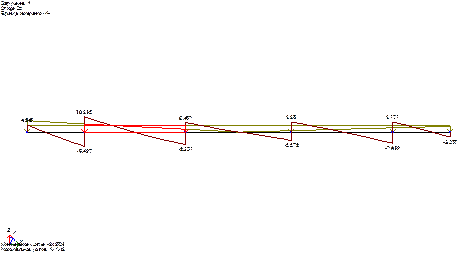
Рис. 4.5. – Эпюра поперечных сил верхнего неразрезного пояса
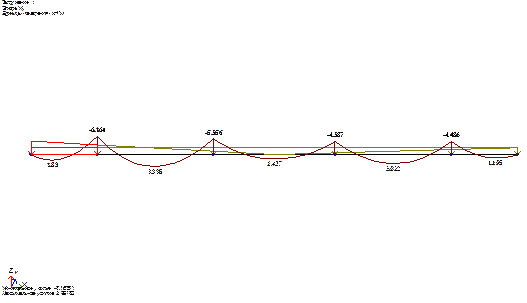
Рис. 4.6. – Эпюра изгибающих моментов верхнего неразрезного пояса
Определение изгибающих моментов в панелях верхнего пояса от действия продольных сил
Анализ схемы фермы и эпюры балочных изгибающих моментов для верхнего пояса (см. рис. 4.6) приводят к выводу, что расчетной является панель БВ неразрезного верхнего пояса.
Поскольку временная снеговая нагрузка распределена по верхнему поясу фермы неравномерно, то определяем значения изгибающих моментов в панели БВ от действия продольных сил по следующему методу.
Для упрощения расчета полагаем, что на эпюре балочных изгибающих моментов расстояния от опор до нулевых точек в промежутке БВ равны между собой и по хорде составляют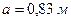 
.
При длине хорды, соединяющей точки Б и В, равной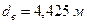 
, стреле выгиба панели верхнего пояса 
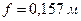и радиусе кривизны оси верхнего пояса 
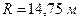получаем следующие значения эксцентриситетов 
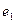и 
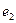, необходимых для вычисления изгибающих моментов от действия продольной силы 
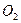соответственно в пролете и на опорах панели.
;
.
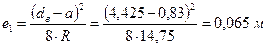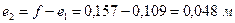Изгибающие моменты от действия продольной силы на опорах составляют:
.
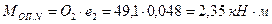Изгибающие моменты от действия продольной силы в пролете составляет:
.
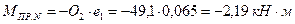Расчетные изгибающие моменты на опорах Б и В составляют:
;
;
.
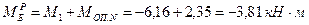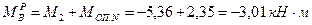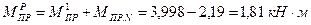Проверка сечения верхнего пояса
Подбор сечения верхнего пояса производим по расчетному изгибающему моменту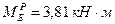 
и расчетной продольной силе 
.
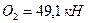При проверке напряжения в опорном сечении Б панели БВ расчетную длину верхнего пояса следует принять равной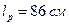 
, т.е. расстоянию от опоры Б до нулевой точки эпюры балочных моментов.
; 
;
;
.
.
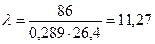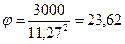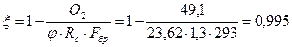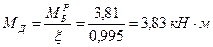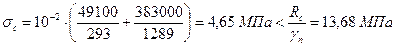Дата: 2019-02-25, просмотров: 315.
