Δx*ΔP≥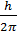

Δx- средняя квадратичная погрешность координаты (неопределенность координаты)

ΔP- средняя квадратичная погрешность импульса ( неопределенность импульса)

    Произведение неопределенностей координаты и соответсвующей ей проекции импульса не может быть меньше величины порядка ħ= 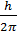=1,06*10^-34 постоянная Планка

В обычном мире, измеряя положение и скорость тела в пространстве, мы на него практически не воздействуем. Таким образом, в идеале мы можем одновременно измерить и скорость, и координаты объекта абсолютно точно (иными словами, с нулевой неопределённостью). В мире квантовых явлений, однако, любое измерение воздействует на систему (поскольку само измерение происходит тоже при помощи квантов, взаимодействующих с измеряемой частицей). Сам факт проведения измерения, например, местоположения частицы, приводит к изменению её скорости, причем непредсказуемому (и наоборот). На самом деле, если удастся с нулевой погрешностью (абсолютно точно) определить одну из измеряемых величин, неопределённость другой величины будет равняться бесконечности, и о ней не будет известно вообще ничего. Иными словами, если бы нам удалось абсолютно точно установить координаты квантовой частицы, о её скорости мы не имели бы ни малейшего представления; если бы нам удалось точно зафиксировать скорость частицы, мы бы понятия не имели, где она находится.

Уравнение Шредингера. Волновая функция и ее физический смысл

В квантовой механике состояние любой квантовой систему описывается волновой функцией Ψ(x,y,z,t). Описание объекта при этом носит вероятностный характер. Квадрат модуля волновой функции плотность вероятности в данный момент t в единичном V в окрестности точки с координатами x,y,z

Физический смысл имеет не сама волновая функция, а квадрат ее модуля w= |Ψ(x,y,z,t)|²

Вероятность найти частицу в объеме V равна: W=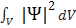

    Условие нормировки волновой функции W= 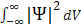=1

       Для того чтобы волновая функция являлась объективной характеристики, она должна удовлетворять нескольким условиям:

· Она должна быть конечной, потому что вероятность не может быть больше 1

· Функция должна быть однозначной

· Функция должна быть не прерывной, потому что вероятность не может меняться скачком

В квантовой механике движение частиц в различных силовых полях описывается уравнением Шредингера: ΔΨ+ 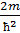(E-U) Ψ=0- для стационарных состояний

Δ- оператор Лапласа (сумма вторых производных по координатам)

E- полная энергия квантовой системы

U- потенциальная энергия квантовой системы

m- масса электрона