Описание светового потока в квантовом приближении

Законы равновесного теплового излучения

Тепловое излучение- единственный вид электромагнитного излучения, которое может быть равновесным. Равновесным называется излучение, для которых выполняется:

1. Тв-ва=Tокр.среды

2. Выполняется принцип детального равновесия.

Для каждой λ, энергия поглащ. равна энергии излуч. тела

Закон Стефана-Больцмана – энергетическая светимость абсолютно черного тела прямо пропорциональна абсолютной температуре тела в четвертой степени: R_э= σ*T⁴ , где σ=5,7·10^-8 ВТ/м²*K4 – постоянная Стефана-Больцмана.

Закон смещения Вина – длина волны, на которую приходится максимум спектральной плотности энергетической светимости абсолютно черного тела обратно пропорциональна абсолютной температуре тела: λ_max= В/T, где В=2,9⋅10-5 м⋅К – постоянная Вина.

Второй закон Вина – максимальная спектральная плотность энергетической светимости абсолютно чёрного тела прямо пропорциональна абсолютной температуре тела в пятой степени: где С=1,3·10^-3 Вт/(м³·К⁵) – постоянная Вина.

Приведенные законы были получены экспериментальным путём. В то же время, многочисленные попытки теоретически получить эти законы оказывались неудачными. Только в 1900 году Планку, на основе допущения о том, что тела могут излучать и поглощать энергию дискретно в виде определённых порций (квантов) и используя законы статической физики получил правильную формулу для спектральной плотности энергетической светимости абсолютно черного тела, которую называют “формула Планка”:

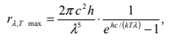, где с – скорость света в вакууме, λ – длина волны света, k = 1,38·10-23 Дж/К – постоянная Больцмана, Т – абсолютная температура тела, энергия кванта света полагается равной E = hν =hc/λ, здесь h = 6.63·10-34 Дж·с – постоянная Планка, ν – частота света. Формула Планка даёт возможность получить и описать все экспериментально полученные законы теплового излучения.

Формула Планка, полученная в предположении о квантовой природе света, даёт правильное, совпадающее с опытом описание всех особенностей и закономерностей равновесного излучения абсолютно чёрного тела. На основе волновых представлений о свете этого сделать нельзя.

Оптическая пирометрия

Оптическая пирометрия- совокупность бесконечных оптических методов измерения температуры.

Эти методы основаны на изменение характеристик излучения нагретого тела и сравнения их с характеристиками абсолютно черного тела.

В зависимости от того, какой закон излуч. иследуют различают: яркостную, цветовую, радиационную

В основе оптических бесконтактных методов измерения температуры лежат законы излучения абсолютно черного тела:

1) Метод, основанный на законе Стефана-Больцмана, заключается в измерении энергии, излучаемой за единицу времени с единицы площади исследуемого тела на всех длинах волн. Как уже отмечалось, эта величина представляет собой энергетическую светимость исследуемого тела. Если исследуемое тело является абсолютно черным, то температура, рассчитанная с использованием измеренной энергетической светимости и формулы дает истинную температуру исследуемого тела. Если же исследуемое тело не является абсолютно черным, то рассчитанная таким образом температура называется радиационной. Радиационная температура – это температура абсолютно черного тела, имеющего такую же энергетическую светимость, что и исследуемое тело.

Данный метод имеет смысл применять лишь для измерения температуры объектов близких по своим спектральным характеристикам к абсолютно черному телу.

    2) Метод, основанный на законе смещения Вина, заключается в том, что для исследуемого тела изучается зависимость спектральной плотности энергетической светимости r_λ от длины волны и определяется длина волны, на которую приходится максимум спектральной плотности энергетической светимости.

Если исследуемое тело является абсолютно черным, то полученная таким образом температура будет истинной температурой тела. Если же тело не является абсолютно черным, то измеренная таким методом температура называется цветовой. Цветовая температура – температура абсолютно черного тела имеющего максимум спектральной плотности энергетической светимости на той же длине волны, что и исследуемое тело.

Данный метод измерения температуры можно использовать лишь применительно к объектам, имеющим непрерывный спектр излучения незначительно отличающийся от спектра излучения абсолютно черного тела.

3) В основе яркостного метода лежат особенности человеческого глаза, который с невысокой точностью измеряет абсолютную яркость светящегося объекта (результат измерения сильно зависит от того в каких условиях освещенности находился глаз до начала измерения), но способен с высокой точностью замечать разницу в яркости близко расположенных объектов, особенно если излучение этих объектов имеет одинаковый спектральный состав. Суть метода “исчезающей нити” заключается в том, что на изображение светящейся поверхности исследуемого тела накладывается изображение нити пирометра. Наблюдение ведется через светофильтр, т.е. в узком спектральном интервале. При изменении силы электрического тока в нити пирометра изменяется яркость ее свечения. В ходе измерения необходимо добиться того, чтобы граница изображения нити на фоне исследуемого тела стала неразличимой, т.е. “нить исчезает”. При этом яркость свечения поверхности исследуемого тела оказывается равной с высокой точностью яркости нити пирометра. Обычно температура светящихся объектов измеряется при длине волн λ = 660нм. Яркость свечения нити пирометра градуируется по яркости абсолютно черного тела, поэтому измерив силу тока через нить пирометра можно по специальной градуировочной таблице определить температуру абсолютно черного тела, имеющего такую же яркость на заданной длине волны, что и исследуемое тело. Если исследуемое тело является абсолютно черным, то измеренная таким образом температура является истинной температурой тела. Если же исследуемое тело не является абсолютно черным, то измеренная данным методом температура называется яркостной. Таким образом, яркостная температура – это температура абсолютно черного тела, которое на заданной длине волны имеет такую же яркость, как и исследуемое тело.

Зная яркостную температуру можно рассчитать истинную температуру тела если известен яркостный коэффициент, определяемый как отношение яркости исследуемого тела к яркости абсолютно черного тела при условии, что их температуры одинаковы: K_я= B′_λ(T_И) / B_λ(T_И)  ,где  B′_λ(T_И)  – яркость исследуемого тела на длине волны λ,  B_λ(T_И)– яркость абсолютно черного тела на той же длине волны и при той же температуре T_И , что и температура исследуемого тела.

Теория эффекта Комптона

Эффектом Комптона называется упругое рассеяние коротковолнового электромагнитного излучения (рентгеновского и γ-излучений) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны.

Эффект Комптона — результат упругого столкновения рентгеновских фотонов со свободными электронами вещества. В процессе этого столкновения фотон передает электрону часть своих энергии и импульса в соответствии с законами их сохранения.

Рассмотрим упругое столкновение двух частиц (рисунок конспект 5.6) – налетающего фотона, обладающего импульсом P_ф = hν/с и энергией Е_ф=hν, с покоящимся свободным электроном (энергия покоя W₀ = m₀с²; m₀ – масса покоя электрона). Фотон, столкнувшись с электроном, передает ему часть своей энергии и импульса и изменяет направление движения (рассеивается). Уменьшение энергии фотона означает увеличение длины волны рассеянного излучения. При каждом столкновении выполняются законы сохранения энергии и импульса.

Согласно закону сохранения энергия: W₀ + Е_ф = W+ Е_ф', а согласно закону сохранения импульса P_ф = P_е + P_ф'

W₀ = m₀с² – энергия электрона до столкновения, Е_ф=hν – энергия налетающего фотона, W=m*c² - энергия электрона после столкновения, Еф'=hν' – энергия рассеянного фотона. m₀с²+ hν =m*c + hν'- закон сохранения энергии.

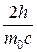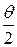 Δλ= sin² -полученная экспериментально Комптоном формула

λ₀= h/m₀*c= 2,4*10^-12м- комптоновская длина волны

    Квадрат амплитуды световой волны в какой- либо точке экрана является мерой вероятности попадания фотона в эту точку экрана. Волновые и квантовые свойства взаимно дополняют друг друга.

Вероятности переходов

Описание светового потока в квантовом приближении