Характеристики, введенные ГОСТ 8.009-84 (ГСИ. Нормируемые метрологические характеристики средств измерений), наиболее полно описывают метрологические свойства СИ. Учитывать все метрологические характеристики СИ при оценивании погрешности результата измерений – сложная и трудоемкая процедура, оправданная при измерениях повышенной точности. При измерениях на производстве и в обиходе такая точность не всегда нужна. В то же время определенная информация о возможной инструментальной составляющей погрешности измерения необходима. Такая информация дается указанием класса точности СИ. Класс точности – это обобщенная характеристика СИ, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности позволяет судить лишь о том, в каких пределах находится погрешность СИ данного типа. Классы точности присваивают СИ при их разработке на основании исследований и испытаний представительной партии средств измерения данного типа. Средство измерений может иметь два и более класса точности (например, при наличии у него двух или более диапазонов измерений одной и той же физической величины; или приборы, предназначенные для измерения нескольких физических величин, также могут иметь различные классы точности для каждой измеряемой величины). Общие положения деления средств измерений по классу точности устанавливает ГОСТ 8.401-80 (ГСИ. Классы точности средств измерений. Общие требования). При этом пределы допускаемых погрешностей нормируют и выражают в форме абсолютных, приведенных или относительных погрешностей, в зависимости от характера изменения погрешностей в пределах диапазона измерений.
Если погрешность результатов измерений в данной области измерений принято выражать в единицах измерений величины или делениях шкалы, то принимается форма абсолютных погрешностей (меры, магазины номинальных ФВ). Если границы абсолютных погрешностей в пределах диапазона измерений практически постоянны, то принимается форма приведенной погрешности, а если эти границы нельзя считать постоянными, то – форма относительной погрешности.
Пределы допускаемой абсолютной погрешности устанавливают по формулам
D = ± а (7)
или
D = ± (а + bx), (8)
где х – значение измеряемой величины; a, b – положительные числа, не зависящие от х.
Нормирование в соответствии с (7) означает, что в составе погрешности средства измерения присутствует только аддитивная составляющая, а в соответствии с (8) – и аддитивная, и мультипликативная составляющие.
Классы точности СИ, выраженные через абсолютные погрешности, обозначают прописными буквами латинского алфавита или римскими цифрами. При этом чем дальше буква от начала алфавита, тем больше значения допускаемой абсолютной погрешности.
Пределы допускаемой приведенной погрешности определяют по формуле
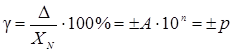, (9)
где Х N – нормирующее значение, выраженное в тех же единицах, что и х (обычно принимается верхний предел измерения для приборов с односторонней шкалой или сумма пределов для приборов с нулем посередине); р – отвлеченное положительное число, выбираемое из стандартизованного ряда значений (1×10n; 1,5×10n; 2×10n; 2,5×10n; 4×10n; 5×10n; 6×10n, где n = 1,0,–1,–2 и т.д.).
Для измерительных приборов с существенно неравномерной шкалой нормирующее значение устанавливают равным длине шкалы. В этом случае класс точности, например, 1,5 означает, что g=1,5% длины шкалы.
Класс точности через относительную погрешность СИ назначается двумя способами:
· если погрешность СИ имеет в основном мультипликативную составляющую, то пределы допускаемой основной относительной погрешности устанавливают по формуле
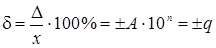, (10)
где q – отвлеченное положительное число, выбираемое из стандартизованного ряда значений;
· если СИ имеют как мультипликативную, так и аддитивную составляющие, то класс точности обозначается двумя цифрами, соответствующими значениям c и d формулы
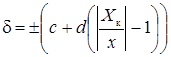%, (11)
где Хк – больший по модулю из пределов измерений (верхний предел измерения, или сумма пределов измерения для приборов с нулем посередине); с, d – положительные числа, выбираемые из стандартизованного ряда. Причем, как правило, c>d. Например, класс точности 0,02/0,01 означает, что с=0,02, а d=0,01, т.е. приведенное значение относительной погрешности к началу диапазона измерения gн=0,02%, а к концу – gк=0,01%.
Пределы допускаемых дополнительных погрешностей, как правило, устанавливают в виде дольного значения предела допускаемой основной погрешности.
Обозначения классов точности в документах и на приборах приведены в табл. 1.
Таблица 1
Формулы вычисления погрешностей и обозначение классов точности СИ
| Вид погреш-ности | Формула по тексту | Примеры пределов допускаемой погрешности | Обозначение класса точности | СИ, рекомендуемые к обозначению таким способом | |
| в НТД | на СИ | ||||
| Абсо-лютная | D = ± а D = ± (а + bx) | D = ± 0,2 А | Класс точности N или класс точности III | N III | Меры То же |
|
| (10) | d=±0,5 % | Класс точности 0,5 | Мосты переменного тока, счетчики, делители, измерительные трансформаторы | |
| (11) |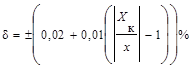 
| Класс точности 0,02/0,01 | 0,02/0,01 | Цифровые СИ, магазины емкостей (сопротивлений) | |
|
| (9) | а) при XN=Хк g=±1,5% | Класс точности 1,5 | 1,5 | Аналоговые СИ; если XN в единицах величины |
| б) XN – длина шкалы или ее части, мм g=±0,5% | Класс точности 0,5 | 0,5 | Омметры; если XN определяется длиной шкалы или ее части | ||
Отно-ситель-ная
Приве-денная
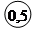ПРИМЕР. Отсчет по шкале прибора с пределами измерений 0 – 50 А и равномерной шкалой составил 25 А. Пренебрегая другими видами погрешностей измерения, оценить пределы допускаемой абсолютной погрешности этого отсчета при использовании различных СИ класса точности: 0,02/0,01; и 0,5.
1. Для СИ класса точности 0,02/0,01:
.
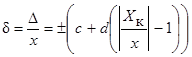Так как х=25; Хк=50; с=0,02; d=0,01 и d – в %, то
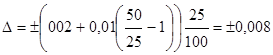А.
2. 
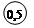Для СИ класса точности :
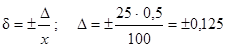А.
3. Для СИ класса точности 0,5:
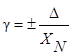; здесь Х N=50, тогд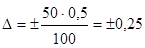а 
А.
Дата: 2019-02-25, просмотров: 226.
