СРЕДСТВ ИЗМЕРЕНИЙ
Для оценки пригодности СИ к измерениям в известном диапазоне с известной точностью вводят метрологические характеристики СИ с целью: обеспечения возможности установления точности измерений; достижения взаимозаменяемости СИ, сравнения СИ между собой и выбора нужных СИ по точности и другим характеристикам; определения погрешностей измерительных систем и установок на основе метрологических характеристик входящих в них СИ; оценки технического состояния СИ при поверке.
По ГОСТ 8.009-84 устанавливают перечень метрологических характеристик, способы их нормирования и формы представления. На практике наиболее распространены следующие метрологические характеристики СИ.
Диапазон измерений – область значений измеряемой величины, для которой нормированы допускаемые пределы погрешности СИ (для преобразователей – это диапазон преобразования).
Предел измерения – наибольшее или наименьшее значение диапазона измерения.
Цена деления шкалы – разность значений величин, соответствующих двум соседним отметкам шкалы. Для приборов с неравномерной шкалой нормируется минимальная цена деления.
Чувствительность – отношение изменения сигнала Dу на выходе СИ к вызвавшему это изменение изменению Dх сигнала на входе:
S=Dy/Dx.
Говоря о чувствительности, указывают чувствительность тока, напряжения и т.д.
Порог чувствительности – наименьшее значение измеряемой величины, вызывающее заметное изменение показаний прибора.
Величину, обратную чувствительности, называют постоянной прибора C=1/S.
Вариация (гистерезис) – разность между показаниями СИ в данной точке диапазона измерения при возрастании и убывании измерений величины и неизменных внешних условиях.
Зависимость между выходным и входным сигналом СИ, полученную экспериментально, называют градуировочной характеристикой, которая может быть представлена аналитически (уравнение преобразования), графически или в виде таблицы. Градуировочная характеристика может изменяться под воздействием внешних и внутренних причин. Например, при быстром изменении тока подвижная часть СИ, вследствие инерции, не успевает «следить» за изменением тока. Градуировочная характеристика в этом случае должна выражаться дифференциальным уравнением.
Основная метрологическая характеристика СИ – погрешность СИ – есть разность между показаниями СИ X и истинными (действительными) значениями ФВ Q.
Основные понятия теории погрешностей
Качество средств и результатов измерений принято характеризовать, указывая их погрешности.
Погрешность результата каждого конкретного измерения складывается из многих составляющих, обязанных своим происхождением различным факторам и источникам. Классификация погрешностей измерения приведена на рис. 7.
По характеру проявления погрешности делятся на случайные, систематические, прогрессирующие и грубые (промахи).
Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же ФВ, проведенных с одинаковой тщательностью в одних и тех же условиях. Случайная составляющая погрешности возможна из-за трения в опорах подвижной части прибора, колебаний температуры окружающего воздуха, влияния магнитных и электрических промышленных помех и т.п. В появлении таких погрешностей не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения; их можно уменьшить путем увеличения числа наблюдений и последующей математической обработкой экспериментальных данных.
 |
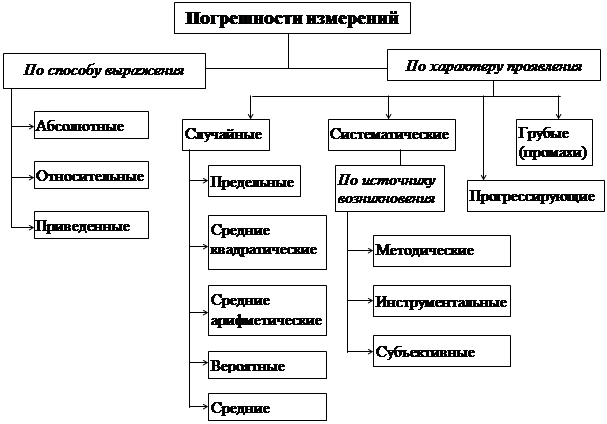Рис.7. Классификация погрешностей измерения
Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же ФВ. Источником систематической погрешности может послужить, например, неточное нанесение отметок на шкалу стрелочного прибора, деформация стрелки. Отличаются от случайных тем, что они могут быть предсказаны, обнаружены и благодаря этому почти полностью устранены введением соответствующей поправки.
Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени. Их отличительные особенности:
- они могут быть скорректированы поправками только в данный момент времени, а далее вновь непредсказуемо изменяются;
- изменения прогрессирующих погрешностей во времени – нестационарный случайный процесс.
Понятие прогрессирующей погрешности широко используется при исследовании динамики погрешностей средств измерений и их метрологической надежности.
Грубая погрешность (промах) – это случайная погрешность результата отдельного наблюдения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Возникают из-за ошибок или неправильных действий оператора, а также кратковременных резких изменений условий проведения измерений. Эти результаты обычно отбрасывают.
По способу выражения различают абсолютную, относительную и приведенную погрешности.
Абсолютная погрешность описывается формулой
D = X – Q (1)
и выражается в единицах измеряемой величины. Однако она не может в полной мере служить показателем точности измерений, так как одно и то же ее значение, например, D=0,05 мм при Х=100 мм соответствует достаточно высокой точности измерений, а при Х=1 мм – низкой. Поэтому и вводится понятие относительной погрешности.
Относительная погрешность – это отношение абсолютной погрешности измерения к истинному значению измеряемой величины:
d = D/ Q = (X – Q)/Q. (2)
Относительную погрешность часто выражают в процентах истинного значения измеряемой величины, т.е. используют вместо (2) формулу
d = [ (X – Q)/Q ] ×100%.
Эта наглядная характеристика точности результата измерения не годится для нормирования погрешности средства измерения, так как при изменении значений Q d принимает различные значения вплоть до бесконечности при Q=0. В связи с этим для указания и нормирования погрешности средства измерения используется еще одна разновидность погрешности – приведенная.
Приведенная погрешность – это относительная погрешность, в которой абсолютная погрешность средства измерения отнесена к условно принятому значению ХN, постоянному во всем диапазоне измерений или его части:
g = D/ХN = (X – Q)/ХN. (3)
Условно принятое значение ХN называют нормирующим (чаще всего за него принимают верхний предел измерений данного средства измерения).
Обязательными компонентами любого измерения являются средство измерения, метод измерения и человек, проводящий измерение. Несовершенство каждого из этих компонентов приводит к появлению своей составляющей погрешности результата.
В соответствии с этим по источнику возникновения различают инструментальные, методические и субъективные погрешности.
Инструментальная погрешность обусловлена погрешностью применяемого средства измерения. Иногда ее еще называют аппаратурной. Причинами инструментальных погрешностей являются: неточность градуировки, конструктивные несовершенства, изменения характеристик прибора в процессе эксплуатации и т.д.
Методическая погрешность измерения происходит от несовершенства метода измерения, использования упрощающих предположений и допущений при выводе применяемых формул, влияния измерительного прибора на объект измерения. Например, измерение температуры с помощью термопары может содержать методическую погрешность, вызванную нарушением температурного режима исследуемого объекта (вследствие внесения термопары).
|
|
|
|
|
|
|
|
|
,
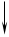
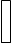
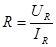а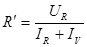 
и методическая погрешность DR=R ¢ - R. Методическая погрешность стремится к нулю при IV ® 0, т.е. при сопротивлении вольтметра RV ® ¥.
Субъективная (личная) погрешность измерения обусловлена погрешностью отсчета оператором показаний по шкалам средства измерения, диаграммам регистрирующих приборов. Использование цифровых приборов и автоматических методов измерения позволяет исключить такого рода погрешности.
Таким образом, каждому из приборов, использованных при измерении, присущи определенные погрешности, причем в общей погрешности прибора может присутствовать и систематическая, и случайная составляющие. Очевидно, что эти составляющие окажут свое влияние на результат измерения, и их следует классифицировать как инструментальные. И, наконец, из-за отсутствия правильных навыков работы с приборами экспериментатор может внести в результат измерения личную составляющую погрешности из-за неточности отсчета доли деления по шкале, невнимательности и др.
По зависимости абсолютной погрешности от значений измеряемой величины различают погрешности (рис. 9):
- аддитивные Dа, не зависящие от измеряемой величины;
- мультипликативные Dм, которые прямо пропорциональны измеряемой величине;
- нелинейные Dн, имеющие нелинейную зависимость от измеряемой величины.
 |
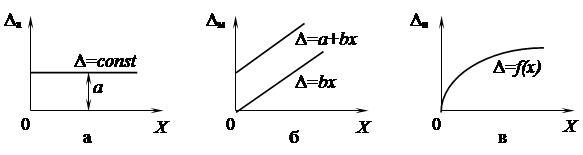Рис. 9. Аддитивная (а), мультипликативная (б) и нелинейная (в) погрешности
Аддитивной, например, является систематическая погрешность, вызванная неточной установкой нуля у стрелочного прибора с равномерной шкалой; мультипликативной – погрешность измерения отрезков времени отстающими или спешащими часами. Такая погрешность будет возрастать по абсолютной величине до тех пор, пока владелец часов не выставит их правильно по сигналам точного времени.
Эти погрешности применяют в основном для описания метрологических характеристик СИ.
По влиянию внешних условий различают основную и дополнительную погрешности СИ. Основной называется погрешность СИ, определяемая в нормальных условиях его применения. Для каждого СИ в нормативно-технических документах оговариваются условия эксплуатации – совокупность влияющих величин (температура окружающей среды, влажность, давление, напряжение и частота питающей сети и др.), при которых нормируется его погрешность. Дополнительной называется погрешность СИ, возникающая вследствие отклонения какой-либо из влияющих величин.
ПРИМЕР. Амперметр предназначен для измерения переменного тока с номинальной частотой (50±5) Гц. Отклонение частоты за эти пределы приведет к дополнительной погрешности измерения.
Для оценивания дополнительных погрешностей в документации на СИ обычно указывают нормы изменения показаний при выходе условий измерения за пределы нормальных.
В зависимости от влияния характера изменения измеряемых величин погрешности СИ делят на статические и динамические. Статическая погрешность – это погрешность СИ применяемого для измерения ФВ, принимаемой за неизменную. Динамической называется погрешность СИ, возникающая дополнительно при измерении переменной ФВ и обусловленная несоответствием его реакции на скорость (частоту) изменения измеряемого сигнала (например, из-за инерционности применяемых технических средств при достаточно быстрых изменениях измеряемой величины).
При измерениях детерминированных сигналов динамические погрешности обычно рассматриваются как систематические. При случайном характере измеряемой величины динамические погрешности приходится рассматривать как случайные.
Принципы описания и оценивания погрешностей. Оценивание погрешностей производится с целью получения объективных данных о точности результата измерения. Точность результата измерения характеризуется погрешностью. При оценке погрешности надо помнить, что излишняя точность ведет к неоправданному расходу средств и времени, а недостаточная точность в зависимости от цели измерения может привести к признанию годным в действительности негодного изделия, к принятию ошибочного решения и т.п.
В основе современных подходов к оцениванию погрешностей лежат принципы, обеспечивающие выполнение требований единства измерений.
Систематическая погрешность по определению может быть представлена постоянной величиной либо известной зависимостью (линейная, периодическая и другие функции от времени или номера наблюдения). Общей моделью случайной погрешности служит случайная величина, обладающая функцией распределения вероятностей.
Характеристики случайной погрешности делятся на точечные и интервальные. К точечным относятся средние квадратические отклонения случайной погрешности, дисперсия; к интервальным – границы неопределенности результата измерения (это означает, что границы, в которых может находиться погрешность, находят как отвечающие некоторой вероятности). Если эти границы определяются как отвечающие некоторой доверительной вероятности, то они называются доверительными интервалами. Если же минимально возможные в конкретном случае границы погрешности оценивают так, что погрешность, выходящую за них, встретить нельзя, то они называются предельными (безусловными) интервалами.
В целях единообразия представления результатов и погрешностей измерений показатели точности и формы представления результатов измерений стандартизованы.
Дата: 2019-02-25, просмотров: 266.
