Для характеристики структуры совокупности применяются особые показатели, которые называют структурные средние величины. Их используют для изучения внутреннего строения и структуры рядов распределения значений признака.
К основным видам структурных средних относят моду и медиану.
Мода – величина признака, которая чаще всего встречается в данной совокупности.
В вариационном дискретном ряду модой является варианта, имеющая наибольшую частоту.
В вариационном интервальном ряду модой считается центральный вариант модального интервала (интервала с наибольшей частотой).
Для расчета моды интервального ряда используется формула:
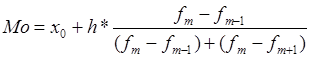 , где
, где
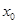 - нижняя граница модального интервала (наименьшее значение признака в интервале),
- нижняя граница модального интервала (наименьшее значение признака в интервале),
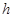 - величина модального интервала (разность между наибольшим и наименьшим значением признака в интервале),
- величина модального интервала (разность между наибольшим и наименьшим значением признака в интервале),
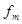 - частота модального интервала,
- частота модального интервала,
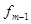 - частота интервала, предшествующего модальному интервалу,
- частота интервала, предшествующего модальному интервалу,
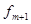 - частота интервала, следующего за модальным интервалом.
- частота интервала, следующего за модальным интервалом.
Рассмотрим расчет моды вариационного интервального ряда на примере задачи №7.
Задача 7.
Имеются данные о распределении организаций по размеру прибыли:
| Сумма прибыли, тыс.руб. | Количество организаций |
| 120-140 | 60 |
| 140-160 | 90 |
| 160-180 | 100 |
| 180-200 | 110 |
| 200-220 | 40 |
| Итого | 400 |
Определите моду.
Решение:
Наибольшей частотой является 110 организаций.
Этой частоте соответствует интервал 180-200 тыс.руб.
Соответственно, интервал 180-200 является модальным интервалом.
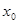 =180
=180
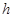 =200-180=20
=200-180=20
Значения модального интервала подставляем в формулу для расчета моды:
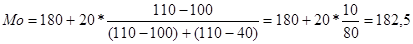 тыс.руб.
тыс.руб.
Ответ: в совокупности из 400 организаций наиболее типичной является организация с суммой прибыли 182,5 тыс.руб.
Медиана – значение признака, которое находится в середине вариационного ряда.
Медианное значение характеризуется тем, что его кумулятивная частота (сумма накопленных частот) равна половине суммы всех частот или превышает ее.
Для расчета медианы интервального ряда используется формула:
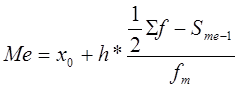 , где
, где
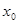 - нижняя граница медианного интервала,
- нижняя граница медианного интервала,
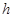 - величина медианного интервала,
- величина медианного интервала,
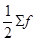 - половина суммы всех частот,
- половина суммы всех частот,
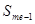 - накопленная частота, предшествующая накопленной частоте медианного интервала,
- накопленная частота, предшествующая накопленной частоте медианного интервала,
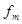 - частота медианного интервала.
- частота медианного интервала.
Рассмотрим расчет медианы вариационного интервального ряда на примере данных задачи №8.
Задача 8.
Имеются данные о распределении организаций по размеру прибыли:
| Сумма прибыли, тыс.руб. | Количество организаций ( f) | Накопленные частоты ( S ) |
| 120-140 | 60 | 60 (переносится) |
| 140-160 | 90 | 150 (60+90) |
| 160-180 | 100 | 250 (150+100) |
| 180-200 | 110 | 360 (250+110) |
| 200-220 | 40 | 400 (360+40) |
| Итого | 400 | х |
Определите медиану.
Решение:
Сумма всех частот (т.е. общее количество организаций) = 400.
Половина суммы всех частот 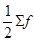 =
= 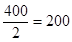 .
.
Выбираем из накопленных частот такую, которая первой по порядку превышает половину всех частот (т.е. больше 200).
Такой частотой является накопленная частота 250.
Накопленной частоте 250 соответствует интервал 160-180 тыс.руб.
Соответственно, интервал 160-180 является медианным интервалом.
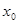 =160
=160
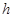 =180-160=20
=180-160=20
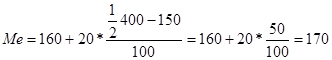 тыс.руб.
тыс.руб.
Ответ: в совокупности из 400 организаций посередине находится организация с суммой прибыли 170 тыс.руб.
Показатели вариации
Вариация – это колеблемость, изменяемость величины признака у отдельных единиц совокупности.
К абсолютным показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.
К относительным показателям вариации относятся: коэффициент осцилляции, относительное линейное отклонение, коэффициент вариации.
Среднее квадратическое отклонение дает обобщающую характеристику размеров вариации признака в совокупности.
Среднее квадратическое отклонение показывает, на какую величину в среднем значение признака отклоняется от стандартного значения.
Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая величина отражает данную совокупность.
Для расчета среднего квадратического отклонения используются формулы:
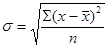 формула применяется, если
формула применяется, если 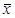 рассчитывалась по формуле средней арифметической простой
рассчитывалась по формуле средней арифметической простой
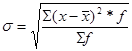 формула применяется, если
формула применяется, если 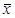 рассчитывалась по формуле средней арифметической взвешенной
рассчитывалась по формуле средней арифметической взвешенной
х – индивидуальные значения признака,
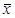 - средняя величина,
- средняя величина,
п – количество индивидуальных значений признака,
f – частота (показывает как часто каждое индивидуальное значение признака повторяется в совокупности).
Коэффициент вариации характеризует меру вариации значений признака вокруг средней величины. Чем меньше коэффициент вариации, тем однороднее совокупность.
Если коэффициент вариации меньше 33%, то это говорит о наименьшей колеблемости признака вокруг средней величины. В этом случае средняя величина является типичной для данной совокупности.
Коэффициент вариации рассчитывается по формуле:
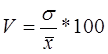 ,где
,где
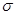 - среднее квадратическое отклонение,
- среднее квадратическое отклонение,
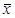 - средняя арифметическая величина.
- средняя арифметическая величина.
Рассмотрим расчет показателей вариации.
Задача 9.
Имеются данные о распределении организаций по размеру прибыли:
| Сумма прибыли, тыс.руб. | Количество организаций ( f) | Середина интервала (х) |
| 120-140 | 60 | (120+140)/2=130 |
| 140-160 | 90 | (140+160)/2=150 |
| 160-180 | 100 | (160+180)/2=170 |
| 180-200 | 110 | (180+200)/2=190 |
| 200-220 | 40 | (200+220)/2=210 |
| Итого | 400 | х |
Решение:
- Определим средний размер прибыли по формуле средней арифметической взвешенной (предварительно рассчитав середину каждого интервала):
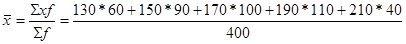 = 169 тыс.руб.
= 169 тыс.руб.
Средний размер прибыли организации составляет 169 тыс.руб.
- Рассчитаем среднее квадратическое отклонение:
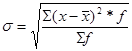 =
= 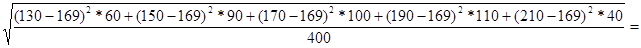
= 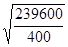 =
= 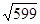 =24,5 тыс.руб.
=24,5 тыс.руб.
Среднее отклонение от среднего размера прибыли составляет 24,5 тыс.руб.
- Определим коэффициент вариации:
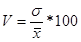 =
= 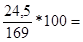 14,5%
14,5%
Совокупность организаций по размеру прибыли является однородной (коэффициент вариации меньше 33%).
Ряды динамики
Одной из важнейших задач статистики является изучение изменений явлений во времени. Эту задачу статистика решает с помощью построения и анализа рядов динамики.
Ряд динамики – это ряд числовых значений статистического показателя, расположенных в совокупности в хронологическом порядке.
Ряд динамики состоит из двух элементов: уровни ряда (у) и время (t).
В зависимости от времени различают моментные и интервальные ряды динамики.
Моментные ряды выражают состояние явления на определенные моменты времени (на начало месяца, квартала, года).
Средний уровень моментного ряда определяется по формуле средней хронологической:
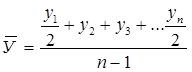 , где
, где
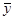 - средний уровень ряда;
- средний уровень ряда;
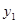 - первый уровень ряда;
- первый уровень ряда;
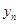 - последний уровень ряда;
- последний уровень ряда;
п – количество уровней ряда.
Рассмотрим применение формулы средней хронологической на примере задачи 10.
Задача 10
Известна списочная численность работников предприятия розничной торговли:
| Дата | На 01.01 | На 01.02 | На 01.03 | На 01.04 |
| Численность работников списочного состава, чел. | 122 | 128 | 126 | 130 |
Определите среднесписочную численность работников предприятия за первый квартал.
Решение:
В задаче представлен моментный ряд динамики, так как значения статистического показателя (численность работников) указаны на точный момент времени, на 1-е число каждого месяца.
В моментных рядах средний уровень определяется по формуле средней хронологической:
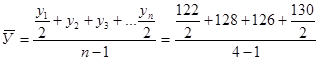 =127 чел.
=127 чел.
Ответ: среднесписочная численность работников за первый квартал составила 127 чел.
Интервальные ряды выражают величину уровней ряда за определенные интервалы времени (за месяц, за год).
Средний уровень интервального ряда определяется по формуле средней арифметической простой:
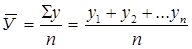 , где
, где
у – уровни ряда;
п – количество уровней.
Рассмотрим расчет среднего уровня интервального ряда на примере задачи.
Задача 11
Имеются данные о численности работников списочного состава розничного торгового предприятия:
| Месяц | Январь | Февраль | Март |
| Численность работников, чел. | 250 | 254 | 255 |
Определите среднесписочную численность работников предприятия за первый квартал.
Решение:
В задаче представлен интервальный ряд динамики, так как значения статистического показателя (численность работников) представлены за определенный промежуток времени (за месяц).
В интервальных рядах средний уровень рассчитывается по формуле средней арифметической простой.
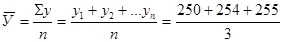 =253 чел.
=253 чел.
Ответ: среднесписочная численность работников предприятия за первый квартал составила 253 чел.
Ряды динамики анализируют с помощью системы показателей, которые можно рассчитать цепным или базисным способом.
При цепном способе расчета каждый текущий уровень ряда сравнивается с предыдущим уровнем.
При базисном способе расчета все уровни ряда сравниваются с одним и тем же уровнем, принятым за базу сравнения.
Причем, если в задании не указан уровень, который необходимо взять за базу сравнения, то подразумевается первый по порядку уровень динамического ряда.
К основным показателям ряда динамики относятся:
- абсолютный прирост,
- темп роста,
- темп прироста,
- абсолютное значение 1% прироста.
Рассмотрим расчет показателей ряда динамики цепным и базисным способом на примере следующей задачи 12.
Задача 12
Розничный товарооборот торгового предприятия за 4 месяца составил:
| Показатели | Январь | Февраль | Март | Апрель |
| Розничный товарооборот торгового предприятия, тыс.руб. | 243,6 | 240,3 | 254,0 | 270,5 |
Определите показатели ряда динамики цепным и базисным способом.
Решение:
1. Абсолютный прирост (Δ 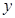 )
)
А) цепной 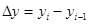 , где , где
| Б) базисный 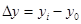 , где , где
|
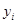 - текущий уровень - текущий уровень
| 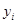 - текущий уровень - текущий уровень
|
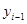 - предыдущий уровень. - предыдущий уровень.
| 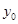 - базисный уровень. - базисный уровень.
|
| 240,3-243,6 = -3,3 тыс.руб. | 240,3-243,6 = -3,3 тыс.руб. |
| 254,0-240,3 = 13,7 тыс.руб. | 254,0-243,6 = 10,4 тыс.руб. |
| 270,5-254,0 = 16,5 тыс.руб. | 270,5-243,6 = 26,9 тыс.руб. |
Вывод: в феврале по сравнению с январем розничный товарооборот предприятия уменьшился на 3,3 тыс.руб. В марте по сравнению с февралем товарооборот увеличился на 13,7 тыс.руб., по сравнению с январем – увеличился на 10,4 тыс.руб. В апреле по сравнению с мартом товарооборот возрос на 16,5 тыс.руб., по сравнению с январем – возрос на 26,9 тыс.руб.
2. Темп роста ( 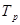 )
)
А) цепной 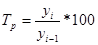
| Б) базисный 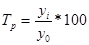
|
| 240,3/243,6*100=98,6% | 240,3/243,6*100=98,6% |
| 254,0/240,3*100=105,7% | 254,0/243,6*100=104,3% |
| 270,5-254,0*100=106,5% | 270,5/243,6*100=111,0% |
Вывод: в феврале произошло снижение товарооборота по сравнению с январем (так как темп роста меньше 100%). В последующие месяцы наблюдается рост товарооборота как по сравнению с предыдущим месяцем, так и по сравнению с базисным январем (так как темп роста больше 100%).
3. Темп прироста ( 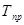 )
)
А) цепной 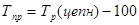
| Б) базисный 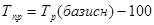
|
| 98,6-100= -1,4% | 98,6-100= -1,4% |
| 105,7-100=5,7% | 104,3-100=4,3% |
| 106,5-100=6,5% | 111,0-100=11,0% |
Вывод: в феврале по сравнению с январем розничный товарооборот уменьшился на 1,4%. В марте по сравнению с февралем товарооборот увеличился на 5,7%, а по сравнению с январем – увеличился на 4,3%. В апреле по сравнению с мартом товарооборот также увеличился на 6,5%, по сравнению с январем – увеличился на 11,0%.
4. Абсолютное значение 1% прироста (А%)
Этот показатель рассчитывается только цепным способом.
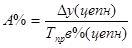
-3,3/ -1,4=2,36 тыс.руб.
13,7/5,7 = 2,40 тыс.руб.
16,5/6,5 = 2,54 тыс.руб.
Вывод: в феврале одному проценту снижения товарооборота соответствует 2,36 тыс.руб., в марте одному проценту роста товарооборота соответствует 2,40 тыс.руб., в апреле 1% роста товарооборота соответствует сумма 2,54 тыс.руб.
Для обобщенной характеристики интенсивности развития исчисляют следующие показатели:
- средний абсолютный прирост;
- средний темп роста;
- средний темп прироста.
Рассмотрим расчет средних показателей ряда динамики на примере задачи № 12.
Решение:
1. Средний абсолютный прирост ( 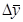 )
)
А) цепной 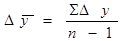 , где
, где
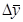 – абсолютный прирост;
– абсолютный прирост;
п – количество уровней ряда.
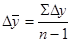 =
= 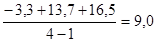 тыс.руб.
тыс.руб.
Б) базисный 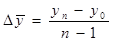 , где
, где
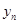 - последний уровень ряда динамики.
- последний уровень ряда динамики.
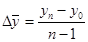 =
= 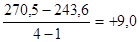 тыс.руб.
тыс.руб.
Вывод: за изучаемые 4 месяца розничный товарооборот торгового предприятия в среднем увеличился на 9,0 тыс.руб.
2. Средний темп роста ( 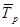 )
)
А) цепной 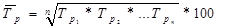 , где
, где
п – количество темпов роста под знаком корня.
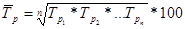 =
= 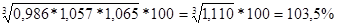
Б) базисный 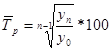 , где
, где
п – количество уровней ряда динамики.
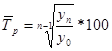 =
= 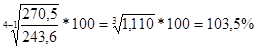
Вывод: среднемесячный рост товарооборота розничного торгового предприятия в изучаемом периоде составил 103,5%.
3. Средний темп прироста ( 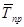 )
)
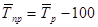 , если
, если 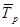 в процентной форме;
в процентной форме;
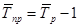 , если
, если 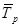 в коэффициентной форме.
в коэффициентной форме.
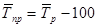 =103,5-100=3,5%
=103,5-100=3,5%
Вывод: за изучаемый период розничный товарооборот торгового предприятия в среднем увеличился на 3,5%.
Индексы
Индексом называется относительный показатель, который характеризует соотношение уровней социально-экономического явления во времени или в пространстве.
При расчете индексов применяются следующие условные обозначения:
I – общий (сводный) индекс;
i – индивидуальный индекс;
р – цена;
g – количество;
pg – товарооборот;
0 – базисный период;
1 – отчетный период.
Индекс как относительный показатель выражается в виде коэффициентов (исчисляется с точностью до 0,001) или процентов (с точностью до 0,1).
- Если в результате сравнения получают индекс больше 1 (или больше 100%), то это означает, что изучаемое явление увеличилось в отчетном периоде по сравнению с базисным.
- Если в результате сравнения получают индекс меньше 1 (или меньше 100%), то изучаемое явление уменьшилось в отчетном периоде по сравнению с базисным.
По степени охвата явления индексы подразделяются на индивидуальные и общие (сводные). Общие (сводные) индексы по форме построения бывают агрегатные и средние.
Рассмотрим построение индивидуальных и агрегатных индексов на примере задачи 13.
Задача 13
Имеются данные о продаже молочных продуктов на городском рынке за два месяца отчетного года:
Наименование продуктов
Июль
Август
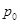
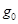
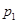
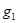
Определите:
1. Индивидуальные индексы цен, физического объема (количества), товарооборота по видам продуктов;
2. Общие индексы цен, физического объема (количества), товарооборота;
3. Абсолютное отклонение товарооборота, в том числе за счет изменения цен и количества проданных продуктов.
Сделайте выводы.
Решение:
Цена обозначается – р, количество проданных продуктов – g.
Отчетным периодом (1) является август, базисным периодом (0) – июль.
1) Индивидуальный индекс цены ( 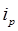 )
)
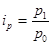 , где
, где
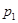 - цена отчетного периода,
- цена отчетного периода,
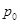 - цена базисного периода.
- цена базисного периода.
А) 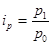 =
= 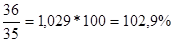
Б) 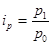 =
= 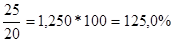
В) 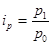
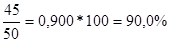
Вывод: в августе по сравнению с июлем цена творога увеличилась на 2,9% (102,9-100); цена сметаны также увеличилась на 25,0% (125,0-100); цена масла уменьшилась на 10,0% (90,0-100).
Индивидуальный индекс физического объема (количества) ( 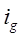 )
)
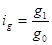 , где
, где
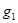 - количество проданного товара отчетного периода;
- количество проданного товара отчетного периода;
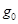 - количество проданного товара базисного периода.
- количество проданного товара базисного периода.
А) 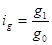 =
= 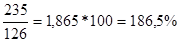
Б) 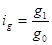 =
= 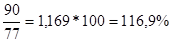
В) 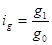 =
= 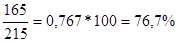
Вывод: в августе по сравнению с июлем количество проданного на рынке творога увеличилось на 86,5% (186,5-100); количество проданной сметаны увеличилось на 16,9% (116,9-100); количество проданного масла сократилось на 23,3% (76,7-100).
Индивидуальный индекс товарооборота ( 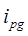 )
)
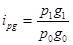 , где
, где
 - товарооборот какого-либо товара в отчетном периоде;
- товарооборот какого-либо товара в отчетном периоде;
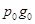 - товарооборот какого-либо товара в базисном периоде.
- товарооборот какого-либо товара в базисном периоде.
А) 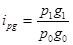 =
= 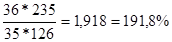
Б) 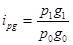 =
= 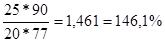
В) 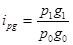 =
= 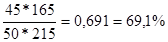
Вывод: в августе по сравнению с июлем товарооборот по творогу увеличился на 91,8% (191,8-100); по сметане - увеличился на 46,1%, по маслу товарооборот уменьшился на 30,9% (69,1-100).
2) Агрегатный индекс цены ( 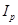 )
)
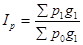 , где
, где
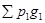 - товарооборот отчетного периода;
- товарооборот отчетного периода;
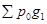 - сопоставимый товарооборот, т.е. количество товаров, проданных в отчетном периоде по ценам базисного периода.
- сопоставимый товарооборот, т.е. количество товаров, проданных в отчетном периоде по ценам базисного периода.
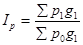 =
= 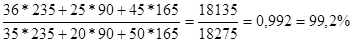
Вывод: за счет изменения цен на молочные продукты товарооборот уменьшился на 0,8% (99,2-100).
Агрегатный индекс физического объема (количества) ( 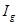 )
)
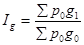 , где
, где
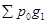 - сопоставимый товарооборот;
- сопоставимый товарооборот;
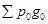 - товарооборот базисного периода.
- товарооборот базисного периода.
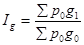 =
= 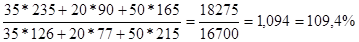
Вывод: за счет изменения количества проданной молочной продукции товарооборот увеличился на 9,4% (109,4-100).
Агрегатный индекс товарооборота ( 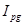 )
)
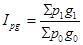 , где
, где
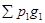 - товарооборот отчетного периода;
- товарооборот отчетного периода;
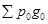 - товарооборот базисного периода.
- товарооборот базисного периода.
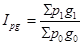 =
= 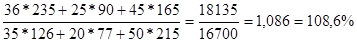
Вывод: в августе по сравнению с июлем товарооборот по молочным продуктам увеличился на 8,6% (108,6-100).
3) Абсолютное отклонение товарооборота ( Δ pg )
Δpg = 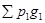 -
- 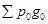
Δpg = 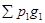 -
- 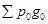 =18135-16700 = +1435 руб.
=18135-16700 = +1435 руб.
Вывод: в августе по сравнению с июлем товарооборот по молочным продуктам увеличился ( так как ответ со знаком «+» ) на 1435 руб.
Абсолютное отклонение товарооборота за счет изменения цен (Δ p )
Δp= 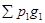 -
- 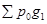
Δp= 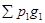 -
- 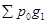 =18135-18275= -140 руб.
=18135-18275= -140 руб.
Вывод: за счет изменения цен на молочную продукцию, товарооборот в августе по сравнению с июлем уменьшился (так как ответ со знаком «-») на 140 руб.
Абсолютное отклонение товарооборота за счет изменения количества проданных товаров ( Δ g )
Δg = 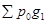 -
- 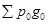
Δg = 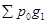 -
- 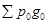 =18275-16700= +1575 руб.
=18275-16700= +1575 руб.
Вывод: за счет изменения количества проданной молочной продукции, товарооборот в августе по сравнению с июлем увеличился на 1575 руб.
Литература
1. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник / Под ред. О.Э. Башиной, А.А. Спирина. – М.: Финансы и статистика, 2001.
2. Практикум по статистике: Учеб пособие для вузов / Под. ред. В.М. Симчеры / ВЗФЭИ. – М.: ЗАО «Финстатинформ», 1999.
3. Теория статистики: Учебник / Под ред. проф. Р.А. Шмойловой. – М.: финансы и статистика, 2001.
Дата: 2019-02-25, просмотров: 303.