Структура оборота, %
3) Вывод:
Наибольшую долю в обороте розничной торговли занимают продовольственные товары, как в прошлом, так и в отчетном году. В отчетном году удельный вес оборота продовольственных товаров незначительно увеличился с 74,8% до 74,9%.
Непродовольственные товары занимают меньшую долю в обороте розничной торговли. В отчетном году по сравнению с прошлым годом удельный вес оборота непродовольственных товаров сократился с 25,2% до 25,1%.
Средние величины
Средняя величина представляет собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Средняя величина выражает типичные черты и дает обобщенную характеристику однотипных явлений по одному из признаков.
Наиболее распространенный вид средней степенной величины – средняя арифметическая.
Средняя арифметическая простая применяется, если данные не сгруппированы, а дается простой перечень значений.
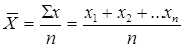, где
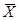– осредняемый признак, т. е. признак, по которому находится средняя величина;
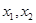…- отдельные значения признака;
n – количество отдельных значений признака.
Рассмотрим применение средней арифметической простой на примере задачи 3.
Задача 3
Имеются данные об объеме выпущенной продукции предприятиями отрасли за отчетный период:
Показатель
№ предприятия
Определите средний объем выпущенной продукции по предприятиям отрасли.
Решение:
х – объем продукции;
n – количество предприятий.
= 
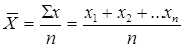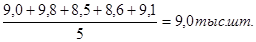
Ответ: объем выпущенной продукции за отчетный период в среднем по предприятиям составил 9,0 тыс.шт.
Средняя арифметическая взвешенная применяется, когда одно и то же значение признака несколько раз встречается в совокупности, т.е., если данные сгруппированы.
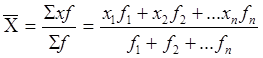, где
f – частота, которая показывает, сколько раз данное значение признака встречается в изучаемой совокупности.
Рассмотрим на примере задачи 4 применение средней арифметической взвешенной.
Задача 4
Имеются данные о заработной плате работников розничного торгового предприятия за отчетный период:
| Заработная плата, руб. | Число работников, чел. |
| 3100 | 2 |
| 4300 | 6 |
| 4600 | 16 |
| 4900 | 12 |
| 5200 | 14 |
Определите средний размер заработной платы работника предприятия за отчетный период.
Решение:
х – заработная плата;
f – число работников.
= 
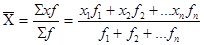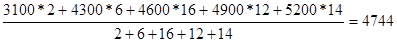руб.
Ответ: средний размер заработной платы работника предприятия составляет 4744 руб.
Средняя гармоническая образуется из обратных значений признака. Средняя гармоническая взвешенная применяется, когда частота (m) представляет собой сложный показатель, состоящий из произведения (x*f).
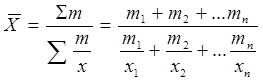, где m – частота.
Рассмотрим применение средней гармонической взвешенной на примере задачи 5.
Задача 5
Имеются данные о заработной плате различных категорий работников розничного торгового предприятия за отчетный период:
| Категория работников | Заработная плата одного работника, руб. | Фонд оплаты труда, руб. |
| Администрация | 4020 | 36180 |
| Продавцы | 2200 | 125400 |
| Прочие работники | 1950 | 11700 |
Определите средний размер заработной платы работника предприятия за отчетный период.
Решение:
х – заработная плата одного работника;
m – фонд оплаты труда
(фонд оплаты труда (m) рассчитывается умножением заработной платы одного работника (x) на количество работников (f).
= 
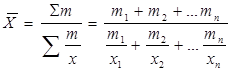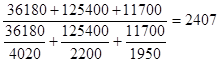руб.
Ответ: средний размер заработной платы работника предприятия составляет 2407 руб.
При расчете средних степенных величин в статистике особое значение имеет правильный выбор вида средней величины. Выбор средней и порядок расчетов зависят от того, какими данными мы располагаем.
Чтобы правильно на практике выбрать формулу средней арифметической или гармонической, необходимо:
А) умножить отдельное значение признака на частоту, и если получается реальный экономический показатель, то для решения задачи следует использовать формулу средней арифметической взвешенной;
Б) разделить частоту на отдельное значение признака, и если получается реальный экономический показатель, то для решения задачи использовать формулу средней гармонической взвешенной.
Задача 6
Имеются данные по предприятию розничной торговли за два квартала:
Магазины
Квартал
Квартал
Определите среднюю производительность труда за 1 квартал, за 2 квартал и за первое полугодие по всему предприятию розничной торговли.
Решение:
Для расчета средней производительности труда за 1 квартал используется формула средней гармонической взвешенной, так как реальный экономический показатель (численность работников) получается при делении частоты на отдельное значение признака:
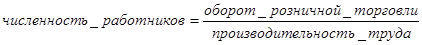
х – производительность труда;
m – оборот розничной торговли.
= 
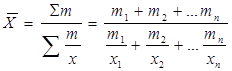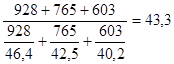тыс. руб.
Для расчета средней производительность труда за 2 квартал используется формула средней арифметической взвешенной, так как реальный экономический показатель (оборот розничной торговли) получается при умножении частоты на отдельное значение признака:
оборот розничной торговли = численность * производительность
работников труда
х – производительность труда;
f – численность работников.
= 
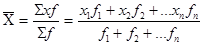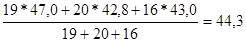тыс.руб.
Для расчета средней производительности труда за первое полугодие необходимо использовать формулу средней арифметической простой, подставив в формулу значения средней производительности труда за 1 квартал и за 2 квартал.
= 
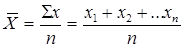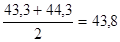тыс.руб.
Ответ: средняя производительность труда работника розничного торгового предприятия составила 43,3 тыс.руб. за 1 квартал, 44,3 тыс.руб. за 2 квартал и 43,8 тыс.руб. за первое полугодие.
Дата: 2019-02-25, просмотров: 219.
