 | |||
 | |||
C,W d W, C1
 |  |  | ||||||
 |  | |||||||
L
В основе диффузионной модели лежит допущение, что структура потока описывается уравнением, аналогичным уравнению молекулярной диффузии. Можно сказать, что это – модель вытеснения, осложненная обратным перемешиванием. Параметром, характеризующим модель служит коэффициент турбулентной диффузии или коэффициент продольного перемешивания. Эта модель описывает реальные аппараты, для которых соблюдаются условия: L/d >20, Re>2320.
Гидродинамическая составляющая описывается следующим уравнением:
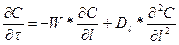
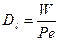- коэффициент продольной турбулентной диффузии,
Ре – критерий Пекле.
4 тип: Модель диффузионного двухпараметрического вытеснения.
| | |||
| | |||
C,W d W, C1
| | | |||||||||
 |  | |||||||||
| | | |||||||||
L
В данной модели учитывается перемешивание потока в продольных и радиальных направлениях. Модель характеризуется коэффициентом продольного и коэффициентом радиального перемешивания. Данная модель соответствует реальным аппаратам. L/d <20, Re>2300.
Гидродинамическая составляющая описывается следующим уравнением:
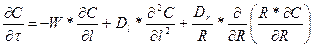
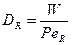- коэффициент турбулентного перемешивания по радиусу ,
Ре – критерий Пекле.
Dr - коэффициент турбулентного перемешивания по радиусу потока,
R – радиус аппарата.
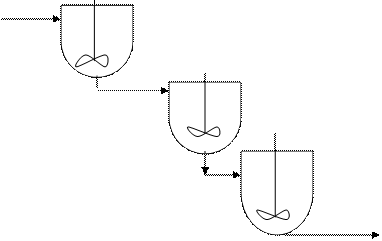
5 тип: ячеечная модель.
Рассматриваемая модель впервые была предложена для каскада реакторов с мешалками.
С01
V1
С02
С1
V2
Vn
С2
С0n ……..
Сn
Основой модели является представление о какой-либо системе разбитой на N количество ячеек. В каждой ячейке осуществляется режим идеального перемешивания и между ячейками отсутствует обратное перемешивание. Модель занимает промежуточное положение между идеальным смешением и идеальным вытеснением. Описывает любые реальные аппараты если верно выбрано число ячеек. Параметром характеризующим модель, служит число ячеек N. C увеличением N структура потока приближается к модели полного вытеснения, а с уменьшением N – к модели идеального смешения
Гидродинамическая модель:
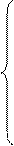
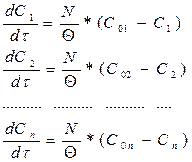
Начальные условия для данной системы : С1 = С02 , С2 = С03 при t = 0. Общий реакционный объём системы: VR=SVn =N*Vn. Предполагается , что каждая ячейка имеет одинаковый объем.
Тепловой баланс системы.
DТ=DТкин.+DТг/д +DТт/о
Температура принадлежит к числу факторов наиболее сильно влияющих на скорость химической реакции, поскольку протекание большинства химических процессов в значительной степени зависит от явления переноса тепла в системе.
Величина DТкинетич в структуре теплового баланса для всех типов моделей записывается как сумма произведений скорости каждой стадии на соответствующий ей тепловой эффект. Скорость стадии берётся по модулю, а знак сомножителя определяется знаком теплового эффекта.
,
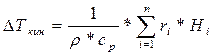где r - плотность реакционной смеси,
ср – теплоемкость реакционной смеси.
Н-р: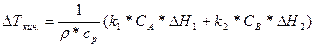 
Следующая составляющая в уравнении теплового баланса гидродинамическая DТгидр, характеризует каким образом изменяется температура в потоке в зависимости от скорости перемешивания потока и конструкционных особенностей аппарата, в котором происходит процесс.
1). Модель идеальное смешение.
Гидродинамическая составляющая описывается следующим уравнением:
; 
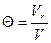; где Т0 – температура потока на входе в аппарат, Т – температура на выходе из аппарата
2). Модель идеальное вытеснение.
Гидродинамическая составляющая описывается следующим уравнением:
.
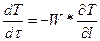3). Модель диффузионное однопараметрическое вытеснение.
Гидродинамическая составляющая описывается следующим уравнением:
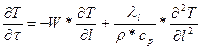,где ll – продольная теплопроводность турбулентного потока
4).Модель диффузионное двухпараметрическое вытеснение.
Гидродинамическая составляющая описывается следующим уравнением:
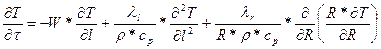
lR – поперечная теплопроводность
5). Ячеечная модель.
Гидродинамическая модель:
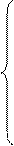
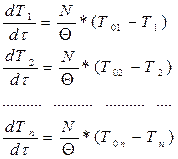
Теплообмен - D Т то.
Учёт стохастической составляющей модели теплообменной аппаратуры позволяет найти распределение температур по длине поверхности теплообмена. Обычно расчёт теплообменной аппаратуры выполняется в следующей последовательности:
1. Составляется тепловой баланс всех потоков приводящих и отводящих тепло Qприх.=Qрасх.
Qпр.=G*Cр*(Тнач - Ткон)
G-количество теплоносителя , Cр- теплоноситель
Тнач,Ткон -начальная и конечная температура теплоносителя.
2). Определяется поверхность теплообмена
F=Qт./k Dtср.t
Анализ процессов, связанных с отводом тепла и теплообменом базируется на исследовании материальных моделей этих процессов, представляющих собой определенные варианты уравнения теплового баланса.
Идеальное смешение.
Модель основана на предположении о полном смешении теплоносителя, поэтому его температура будет постоянной по длине теплообменника.
где К – коэффициент теплопередачи,
F –поверхность теплопередачи,
Т1 –температура потока в аппарате,
Т2 – температура теплоносителя,
Vr – объем аппарата.
Знак «+» - тепло поступает в систему, знак «-» - отвод тепла из системы
Идеальное вытеснение.
В основе модели лежат допущения о постоянстве температуры в поперечном сечении и отсутствии продольного перемешивания.
,
где dR- диаметр трубы теплообменника.
В зависимости от тепловых режимов все реакторы делятся на:
- изотермические,
- адиабатические ,
- политропные.
В изотермических для поддержания постоянной температуры необходимо подводить или отводить тепло. Его количество соответствует суммарному тепловому эффекту всех реакций протекающих в системе. Так как в таком реакторе температура постоянна, то уравнения теплового баланса нет.
DТ= const.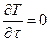 
Однако эти реактора сравнительно редко используются в крупномасштабных производствах из-за высокой стоимости оборудования для съёма или подвода тепла.
Реактор называется адиабатическим, если в системе выделяемое в результате химической реакции тепло полностью идёт на изменение температуры при этом теплообмен с окружающей средой полностью отсутствует. В структуре теплового баланса отсутствует третья составляющая DTто=0.
В политропном реакторе изменение температурного режима в системе происходит и за счёт химической реакции и за счёт теплообмена с окружающей средой.
Дата: 2019-02-25, просмотров: 368.
