Если молекула находится вблизи поверхности, то действие на нее других молекул уже не уравновешивается и приводит к появлению равнодействующей силы, направленной внутрь жидкости. Для увеличения свободной поверхности жидкости часть молекул должна перейти из объема в поверхностный слой, а для этого необходимо совершить некоторую работу. Поэтому существование поверхности жидкости связано с дополнительной энергией.

Поверхностная энергия – это избыток потенциальной энергии молекул в поверхностном слое по сравнению с энергией молекул в объеме вдали от границы.

Сила поверхностного натяжения – это сила, которая действует вдоль поверхности жидкости, перпендикулярно линии (реальной или мысленной), ограничивающей эту поверхность. В существовании силы поверхностного натяжения можно убедиться с помощью следующих простых опытов.

Наиболее наглядны опыты с использованием мыльной пленки. Положим петлю из нитки на мыльную пленку, полученную при обмакивании проволочного каркаса в мыльном растворе. Пока мыльная пленка внутри петли цела, петля сохраняет любую приданную ей форму (рис. а). Если же пленку внутри петли проткнуть, то нить принимает форму окружности (рис. б). Такая форма обеспечивает минимальную площадь оставшейся на каркасе пленки и тем самым минимальное значение ее поверхностной энергии.

Благодаря поверхностному натяжению жидкость в отсутствие внешних сил принимает форму шара, т. е. имеет минимальную при данном объеме поверхность и соответственно минимальную поверхностную энергию. Так бывает в невесомости, например в кабине космического корабля, где невозможно налить воду в стакан, и при свободном падении дождевых капель.

Количественно поверхностное натяжение s характеризуется отношением модуля F силы поверхностного натяжения, действующей на границу поверхностного слоя, к длине границы l, или, что то же самое, отношением поверхностной энергии U _пов к площади S поверхности:

. 

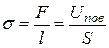В случае плоской поверхности жидкости сила поверхностного натяжения не зависит от того, насколько поверхность «растянута».

Строго говоря, само понятие «растяжение» для такой поверхности лишено смысла: чтобы увеличивать площадь поверхности, вытягивая в поверхностный слой из объема все новые и новые молекулы, необходимо, в отличие от случая растягивания резиновой пленки, прикладывать постоянную силу, так как поверхностный слой, увеличиваясь по площади, не меняет своих свойств.

Именно это свойство сил поверхностного натяжения приводит к эквивалентности двух определений величины s в последней формуле.

В самом деле, работа, совершаемая при перемещении ограничивающей мыльную пленку перемычки длиной l на расстояние х равна

,

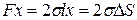где 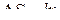 – увеличение площади поверхности одной стороны пленки (учтем, что у пленки две стороны). Эта работа равна приращению поверхностной энергии пленки

.

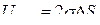Смачивание.

Вследствие взаимодействия молекул жидкости с молекулами твердых тел возникает смачивание – явление, приводящее к искривлению свободной поверхности жидкости у поверхности твердого тела. Если сила взаимодействия между молекулами жидкости и твердого тела больше силы взаимодействия между молекулами самой жидкости, то говорят, что жидкость смачивает твердую поверхность. В этом случае угол q между плоскостью, касательной к поверхности жидкости, и поверхностью твердого тела, называемый краевым углом или углом смачивания, будет острым (рис. а). В противном случае угол q будет тупым (рис. б). При полном смачивании q = 0, при полном несмачивании 0 = p. Например, вода смачивает чистое стекло и не смачивает поверхность, покрытую парафином.

Смачиванием и несмачиванием объясняются многие хорошо знакомые нам явления. Подъем керосина по фитилю лампы, возможность вытереться полотенцем – это примеры явлений, целиком обусловленных смачиванием. Напротив, плавание покрытой тонким слоем жира стальной иголки на поверхности воды, тефлоновые кастрюли и сковородки, в которых не подгорает пища, бегающие по воде на длинных тонких ногах жуки-водомеры – во всех этих случаях мы сталкиваемся с несмачиванием.

Капиллярные явления.

Подъем или опускание жидкости в узких трубках-капиллярах вследствие явления смачивания называются капиллярными явлениями. Высоту h, на которую поднимается жидкость (плотностью r), полностью смачивающая стенки капилляра радиуса r, можно найти, приравнивая вес столбика поднявшейся жидкости силе поверхностного натяжения, действующей по верхнему периметру столбика:

,

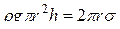откуда

.

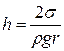Явление капиллярности играет огромную роль в самых разнообразных процессах, происходящих в природе. Например, проникновение влаги из почвы в растения, в стебли и листья обусловлено капиллярностью. Клетки растения образуют капиллярные каналы, и чем меньше радиус капилляра, тем выше по нему поднимается жидкость. Процесс кровообращения тоже связан с капиллярностью. Кровеносные сосуды являются капиллярами.

Особенно большое значение имеет капиллярность почвы. По мельчайшим сосудам влага из глубины перемещается к поверхности почвы. Если хотят уменьшить испарение влаги, то почву рыхлят, разрушая капилляры. В целях увеличения притока влаги из глубины почву укатывают, увеличивая количество капиллярных каналов. В технике капиллярные явления имеют большое значение в процессах сушки, в строительстве.

Вопросы для самоконтроля:

1. Объясните, исходя из молекулярно-кинетической теории строения вещества, упругость, текучесть и вязкость жидкости.

2. От чего зависит поверхностное натяжение?

3. Как направлена сила поверхностного натяжения жидкости?

4. Как определить изменение потенциальной энергии поверхностного слоя жидкости при увеличении или уменьшении ее поверхности?

5. Какие явления можно наблюдать на границе жидкости с твердым телом?

6. Почему уровень однородной жидкости в различных капиллярных трубках сообщающихся сосудов различный?

7. Запишите формулу, по которой определяется высота поднятия (опускания) жидкости по капилляру.